3.1勾股定理(2)课件 (共17张PPT)
文档属性
| 名称 | 3.1勾股定理(2)课件 (共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 21:10:04 | ||
图片预览





文档简介
(共17张PPT)
苏科版 八年级上
苏科版八年级上册
3.1勾股定理(2)
知识回顾
如果设中间直角三角形的两条直角边长分别为a,b,斜边长为c,说一说他们之间的关系,这个关系叫做什么?
b
a
c
如何证明这个定理呢?
想一想
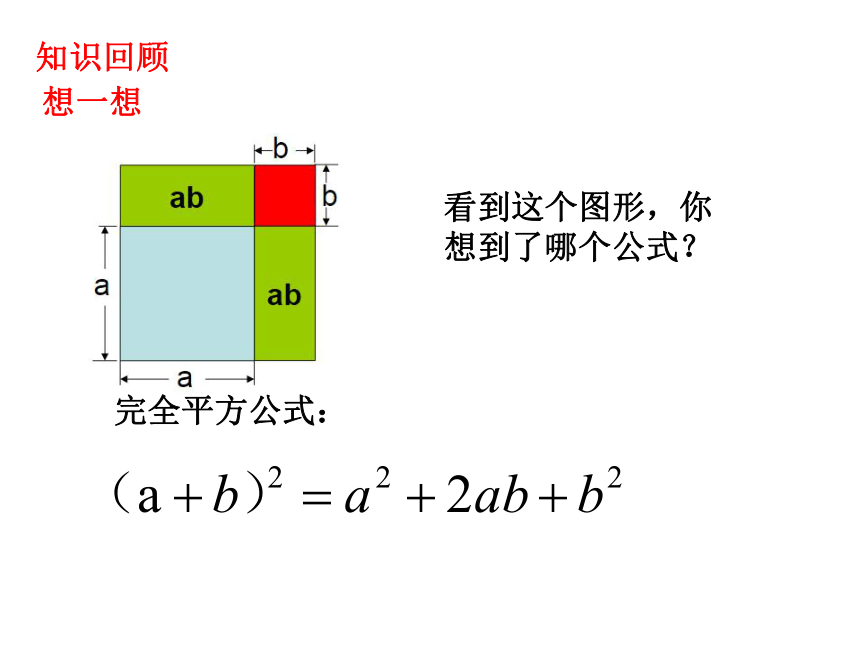
看到这个图形,你想到了哪个公式?
完全平方公式:
知识回顾
活动一
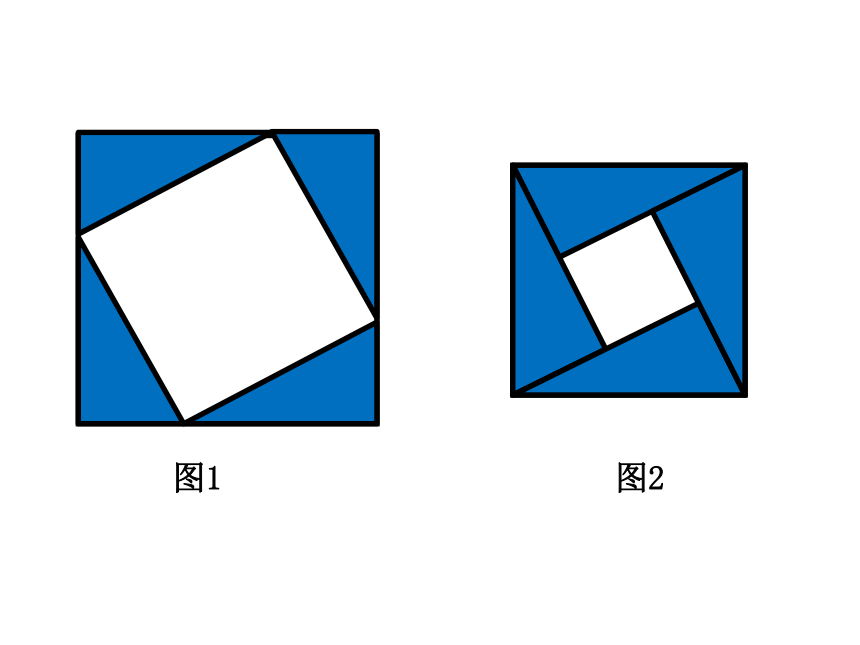
剪四个完全相同的直角三角形,设它的两条直角边长分别为a,b,斜边长为c。然后将它们拼成一个正方形。试试看,你有几种不同的拼法?
探索研究
将拼好的正方形画在任务单上。
图2
图1
b
c
a
,
,
.
太棒了!同学们你们是不是也是这样想的呢?
探索研究
活动二 请同学观察大家拼成的另外一个正方形,用字母将不同的边长表示出来并思考中间那个小正方形的边长是多少呢?
探索研究
b-a
c
a
b
b-a
2002年的世界数学家大会在中国北京举行,这是21世纪数学家的第一次大聚会,这次大会的会标就选定了验证勾股定理的“弦图”作为中央图案,可以说是充分表现了我国古代数学的成就,也充分弘扬了我国古代的数学文化。
我国数学家赵爽的“弦图”
早在公元3世纪,赵爽就用此图形验证了“勾股定理”。
课程拓展
勾2 + 股2 = 弦2
股
勾
勾
较短的直角边称为 ,
股
较长的直角边称为 ,
直角三角形中
弦
斜边称为 。
弦
归纳总结
试一试:
如图,把火柴盒放倒,在这个过程中,也能验证勾股定理,你能利用这个图验证勾股定理吗?把你的想法与大家交流一下.
活动三
自我提升
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
a
b
b
c
c
,
.
自我提升
a
b
c
C
A
B
1、已知:在Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= ;
②若c = 10,b = 8,则a= ;
③若c = 25 ,a = 24 ,则b= .
结论变形
13
6
7
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立相等关系.
方法小结
2、如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,求梯子的顶端与地面的距离h.
新知运用
1、本节课你学到了什么?
小结思考
2、本节课你的哪些能力得到了提升?
https://www.21cnjy.com/help/help_extract.php
苏科版 八年级上
苏科版八年级上册
3.1勾股定理(2)
知识回顾
如果设中间直角三角形的两条直角边长分别为a,b,斜边长为c,说一说他们之间的关系,这个关系叫做什么?
b
a
c
如何证明这个定理呢?
想一想
看到这个图形,你想到了哪个公式?
完全平方公式:
知识回顾
活动一
剪四个完全相同的直角三角形,设它的两条直角边长分别为a,b,斜边长为c。然后将它们拼成一个正方形。试试看,你有几种不同的拼法?
探索研究
将拼好的正方形画在任务单上。
图2
图1
b
c
a
,
,
.
太棒了!同学们你们是不是也是这样想的呢?
探索研究
活动二 请同学观察大家拼成的另外一个正方形,用字母将不同的边长表示出来并思考中间那个小正方形的边长是多少呢?
探索研究
b-a
c
a
b
b-a
2002年的世界数学家大会在中国北京举行,这是21世纪数学家的第一次大聚会,这次大会的会标就选定了验证勾股定理的“弦图”作为中央图案,可以说是充分表现了我国古代数学的成就,也充分弘扬了我国古代的数学文化。
我国数学家赵爽的“弦图”
早在公元3世纪,赵爽就用此图形验证了“勾股定理”。
课程拓展
勾2 + 股2 = 弦2
股
勾
勾
较短的直角边称为 ,
股
较长的直角边称为 ,
直角三角形中
弦
斜边称为 。
弦
归纳总结
试一试:
如图,把火柴盒放倒,在这个过程中,也能验证勾股定理,你能利用这个图验证勾股定理吗?把你的想法与大家交流一下.
活动三
自我提升
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证法。1881年,伽菲尔德就任美国第二十任总统后,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就称这一证法称为“总统”证法。
a
b
b
c
c
,
.
自我提升
a
b
c
C
A
B
1、已知:在Rt△ABC中,∠C=90°.
①若a = 5,b = 12,则c= ;
②若c = 10,b = 8,则a= ;
③若c = 25 ,a = 24 ,则b= .
结论变形
13
6
7
(1)在直角三角形中,已知两边,可求第三边;
(2)可用勾股定理建立相等关系.
方法小结
2、如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,求梯子的顶端与地面的距离h.
新知运用
1、本节课你学到了什么?
小结思考
2、本节课你的哪些能力得到了提升?
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
