6.1 函数(2)课件 (共16张PPT)
文档属性
| 名称 | 6.1 函数(2)课件 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-05 21:00:04 | ||
图片预览





文档简介
(共16张PPT)
苏科版 八年级上
苏科版 八年级上册
6.1函数(2)
一、情境导入:
假设我们班级组织旅游,租用了一辆豪华大巴汽车若汽车以100km/h的速度匀速行驶,在这一变化过程中,
1.有哪些变量?哪些常量?
2.变量之间是函数关系吗?
3.若汽车行驶的时间为t(h),汽车行驶的路程为S(km).怎样表示函数S与自变量t的关系?
t / h 1 2 3 4 5 t
S / km
100
200
300
400
500
100t
s=_____
100t
二.探索新知:
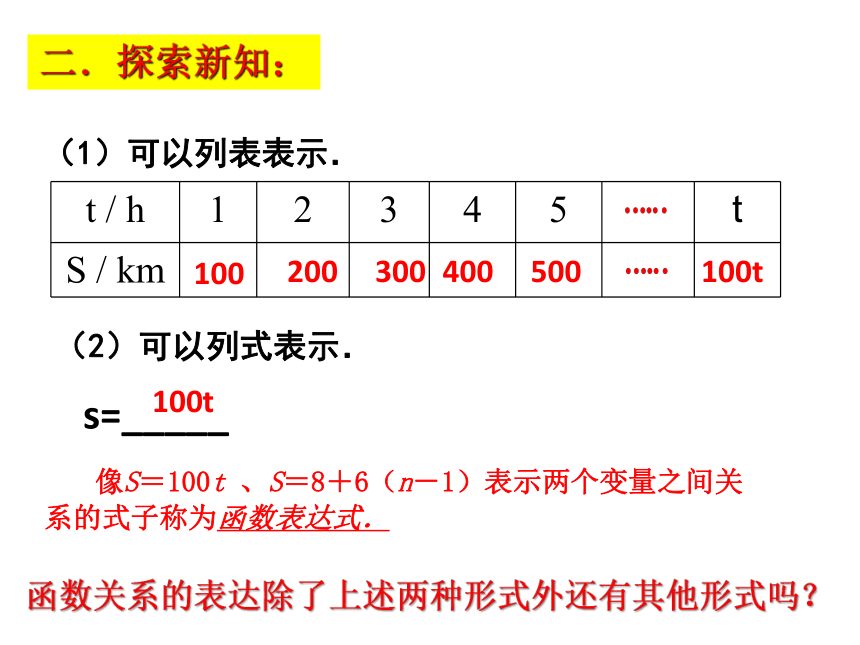
(1)可以列表表示.
(2)可以列式表示.
像S=100t 、S=8+6(n-1)表示两个变量之间关系的式子称为函数表达式.
函数关系的表达除了上述两种形式外还有其他形式吗?
t / h 1 2 3 4 5 t
S / km 100 200 300 400 500 100t
若汽车以100km/h的速度匀速行驶,则路程S与时间t的函数关系能不能用函数图像来描述呢?
像这样,在直角坐标系中,以自变量的值为横坐标,对应的函数值为纵坐标的点所组成的图形叫做这个函数的图像。
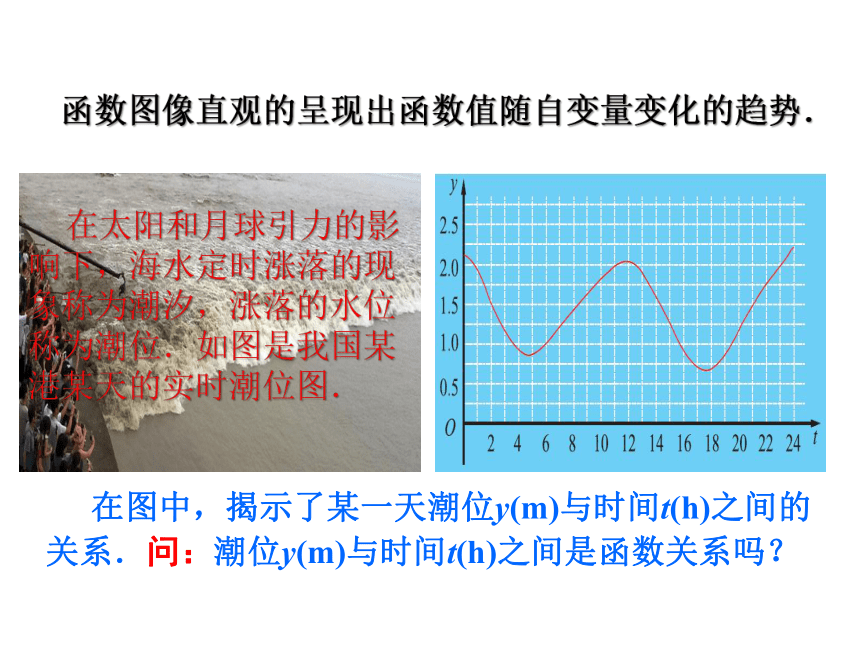
在太阳和月球引力的影响下,海水定时涨落的现象称为潮汐,涨落的水位称为潮位.如图是我国某港某天的实时潮位图.
函数图像直观的呈现出函数值随自变量变化的趋势.
在图中,揭示了某一天潮位y(m)与时间t(h)之间的关系.问:潮位y(m)与时间t(h)之间是函数关系吗?
三、例题精讲:
例题1
一汽车油箱内存油40L,每行驶100km耗油10L.求行驶过程中油箱内剩余油量 Q (L)与行驶路程 s (km) 的函数表达式.
(1)汽车行驶250km时,油箱里还有多少油?
(2)你认为这辆汽车现有油量够它行驶多远?
(3)现在你能确定s的取值范围吗?
注意:在实际问题中,自变量的取值通常有一定的范围.
牛刀小试:
商店有100支铅笔.
(1)如果卖出x支,还剩y 支,那么y= ;
(2)当x越来越大时,y会发生什么变化?
100-x
(3)请写出自变量取值范围
.
0≤ x ≤100,且x为整数
y随x增大而减小.
例2 右图折线是大巴行驶的路程s(km)与时间t(h)之间的函数关系.
在路上花费得时间是 ___小时;
②折线中有一条平行于t轴的线段,试说明它的实际意义
;
③出发5h时,离的起点有多远?
7
300Km
1、一本600页的书,每天看15页,x天后还没看的页数y与天数x之间的函数表达式为
2、等腰三角形的顶角y度与底角x度之间的函数关系式 .
牛刀小试:
y=600-15x
y=180-2x
1、甲出去散步,用20 min走了900 m后,随即按原速返回.下面4个图像中,哪一个表示甲离家的路程s(m)与时间t(min)的函数关系?
学以致用
2、乙出去散步,用20 min走了900 m后,遇到一位朋友,并与朋友交谈了10min后,用15min时间回到家里 .下面4个图像中,哪一个表示甲离家的路程s(m)与时间t(min)的函数关系?
本节课你有什么收获
四.课堂小结:
五.当堂检测:
见学习任务清单
作业
六、布置作业:
必做题:课本P141 ,习题6.1.4、5、6.
《补充习题》P80-81,6.1函数(2)
阅读课本141页《函数小史》了解函数发展史.
谢 谢!
苏科版 八年级上
苏科版 八年级上册
6.1函数(2)
一、情境导入:
假设我们班级组织旅游,租用了一辆豪华大巴汽车若汽车以100km/h的速度匀速行驶,在这一变化过程中,
1.有哪些变量?哪些常量?
2.变量之间是函数关系吗?
3.若汽车行驶的时间为t(h),汽车行驶的路程为S(km).怎样表示函数S与自变量t的关系?
t / h 1 2 3 4 5 t
S / km
100
200
300
400
500
100t
s=_____
100t
二.探索新知:
(1)可以列表表示.
(2)可以列式表示.
像S=100t 、S=8+6(n-1)表示两个变量之间关系的式子称为函数表达式.
函数关系的表达除了上述两种形式外还有其他形式吗?
t / h 1 2 3 4 5 t
S / km 100 200 300 400 500 100t
若汽车以100km/h的速度匀速行驶,则路程S与时间t的函数关系能不能用函数图像来描述呢?
像这样,在直角坐标系中,以自变量的值为横坐标,对应的函数值为纵坐标的点所组成的图形叫做这个函数的图像。
在太阳和月球引力的影响下,海水定时涨落的现象称为潮汐,涨落的水位称为潮位.如图是我国某港某天的实时潮位图.
函数图像直观的呈现出函数值随自变量变化的趋势.
在图中,揭示了某一天潮位y(m)与时间t(h)之间的关系.问:潮位y(m)与时间t(h)之间是函数关系吗?
三、例题精讲:
例题1
一汽车油箱内存油40L,每行驶100km耗油10L.求行驶过程中油箱内剩余油量 Q (L)与行驶路程 s (km) 的函数表达式.
(1)汽车行驶250km时,油箱里还有多少油?
(2)你认为这辆汽车现有油量够它行驶多远?
(3)现在你能确定s的取值范围吗?
注意:在实际问题中,自变量的取值通常有一定的范围.
牛刀小试:
商店有100支铅笔.
(1)如果卖出x支,还剩y 支,那么y= ;
(2)当x越来越大时,y会发生什么变化?
100-x
(3)请写出自变量取值范围
.
0≤ x ≤100,且x为整数
y随x增大而减小.
例2 右图折线是大巴行驶的路程s(km)与时间t(h)之间的函数关系.
在路上花费得时间是 ___小时;
②折线中有一条平行于t轴的线段,试说明它的实际意义
;
③出发5h时,离的起点有多远?
7
300Km
1、一本600页的书,每天看15页,x天后还没看的页数y与天数x之间的函数表达式为
2、等腰三角形的顶角y度与底角x度之间的函数关系式 .
牛刀小试:
y=600-15x
y=180-2x
1、甲出去散步,用20 min走了900 m后,随即按原速返回.下面4个图像中,哪一个表示甲离家的路程s(m)与时间t(min)的函数关系?
学以致用
2、乙出去散步,用20 min走了900 m后,遇到一位朋友,并与朋友交谈了10min后,用15min时间回到家里 .下面4个图像中,哪一个表示甲离家的路程s(m)与时间t(min)的函数关系?
本节课你有什么收获
四.课堂小结:
五.当堂检测:
见学习任务清单
作业
六、布置作业:
必做题:课本P141 ,习题6.1.4、5、6.
《补充习题》P80-81,6.1函数(2)
阅读课本141页《函数小史》了解函数发展史.
谢 谢!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
