6.2向心力 课件(25张PPT)
文档属性
| 名称 | 6.2向心力 课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 26.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-04 19:35:56 | ||
图片预览



文档简介
第六章 圆周运动
6.2 向心力
空中飞椅与人一起做匀速圆周运动的过程中,受到了哪些力?所受合力的方向有什么特点?
温故知新
什么是匀速圆周运动?
物体沿着圆周运动,且线速度的大小处处相等
匀速圆周运动的物体速度是否改变?
速度大小不变方向不断变化
速度变化
具有加速度
合外力不为零合外力有何特点?
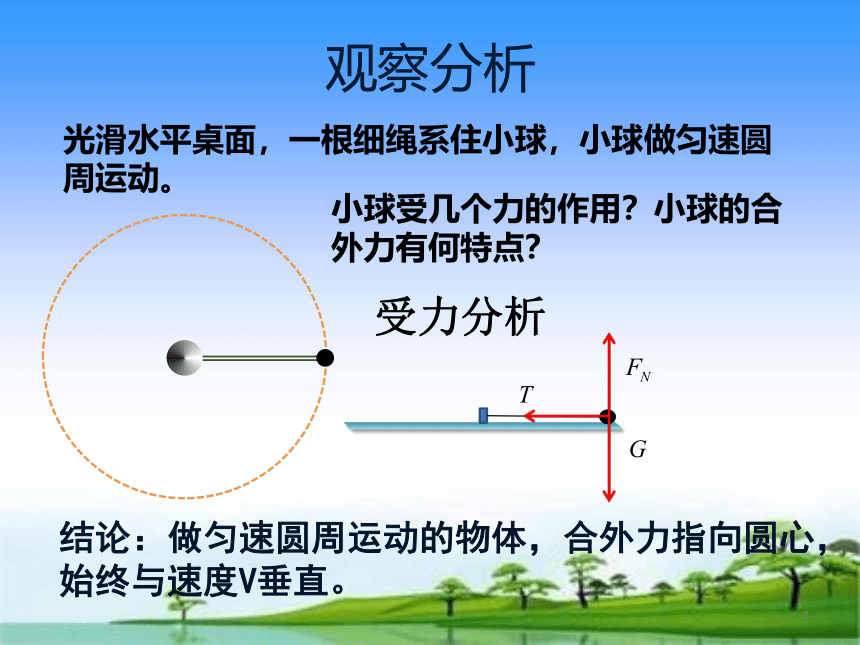
观察分析
光滑水平桌面,一根细绳系住小球,小球做匀速圆周运动。
小球受几个力的作用?小球的合外力有何特点?
受力分析
结论:做匀速圆周运动的物体,合外力指向圆心,始终与速度V垂直。
向心力
1.定义:做匀速圆周运动的物体一定受到
一个指向圆心的合力,这个力叫做向心力。
2.方向:总指向圆心,与线速度垂直,方向不断变化。
3.效果:只改变速度方向,不改变速度大小。
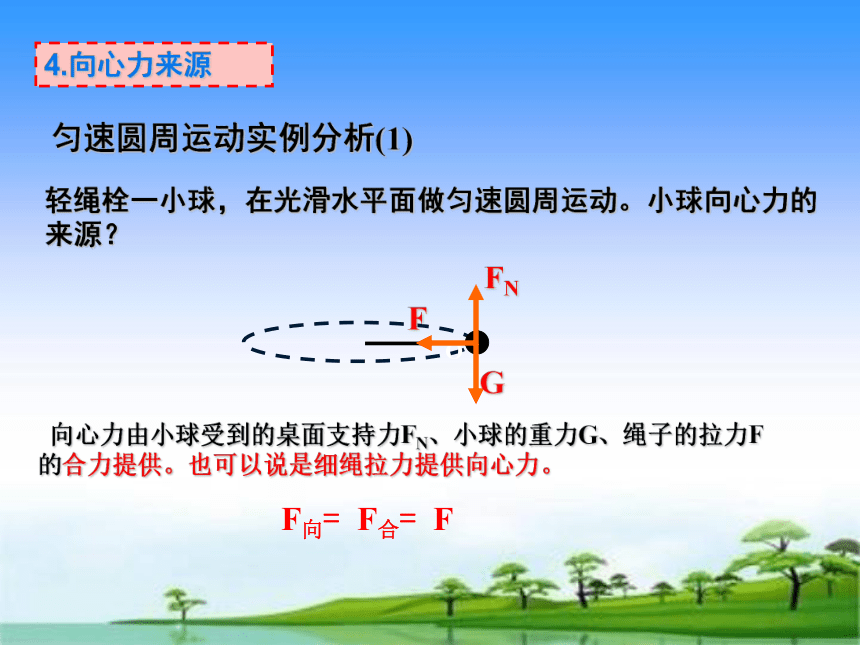
轻绳栓一小球,在光滑水平面做匀速圆周运动。小球向心力的来源?
O
G
FN
F
向心力由小球受到的桌面支持力FN、小球的重力G、绳子的拉力F的合力提供。也可以说是细绳拉力提供向心力。
匀速圆周运动实例分析(1)
F向= F合= F
4.向心力来源
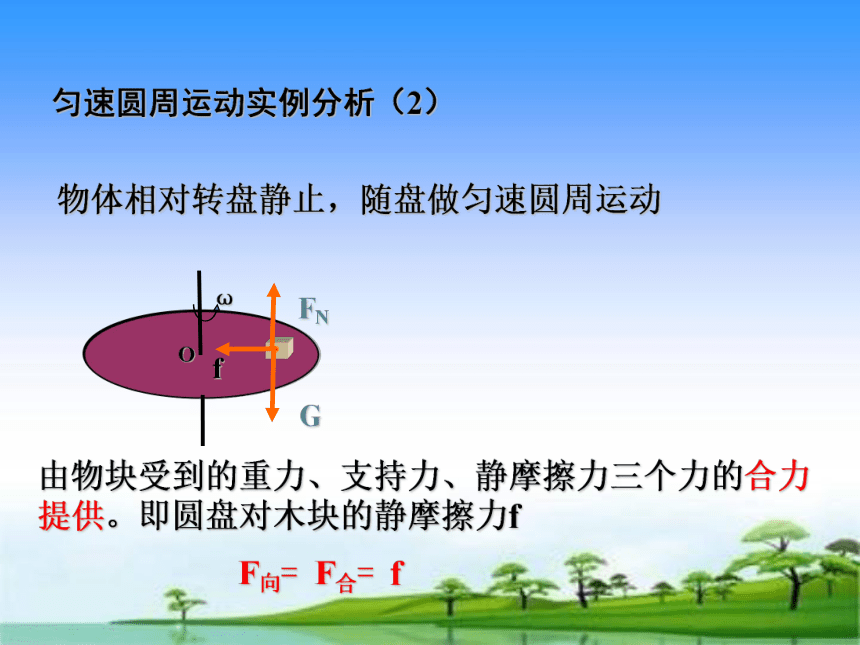
物体相对转盘静止,随盘做匀速圆周运动
F向= F合= f
由物块受到的重力、支持力、静摩擦力三个力的合力提供。即圆盘对木块的静摩擦力f
ω
O
G
FN
f
匀速圆周运动实例分析(2)
G
f
FN
ω
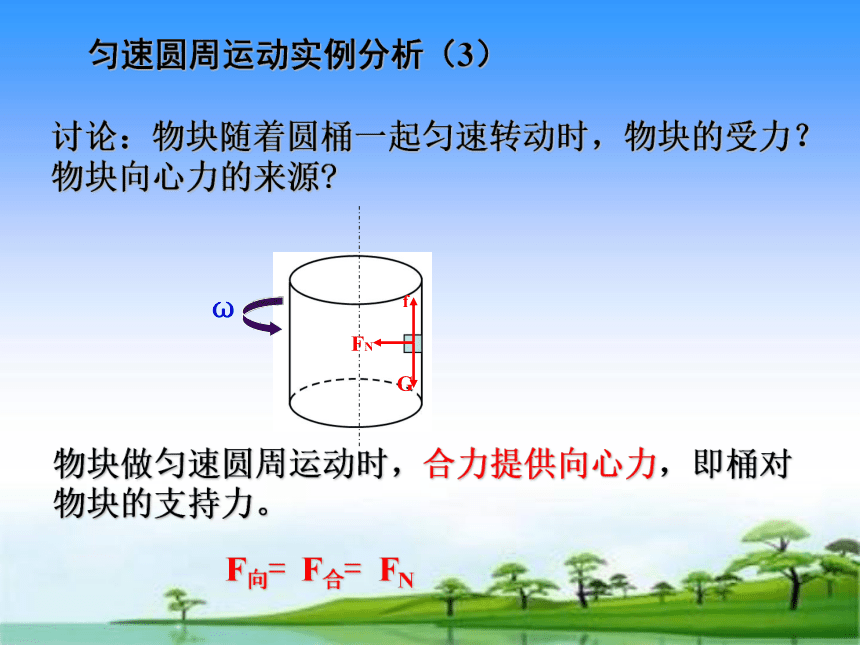
讨论:物块随着圆桶一起匀速转动时,物块的受力?物块向心力的来源?
物块做匀速圆周运动时,合力提供向心力,即桶对物块的支持力。
匀速圆周运动实例分析(3)
学科网
F向= F合= FN
如图:拉力和重力的合力提供物体做匀速圆周运动向心力。
O'
ω
O
θ
l
m
mg
F合
FT
匀速圆周运动实例分析(4)
竖直方向:FN cosθ=mg
水平方向:F合=mg tanθ=mω2 L
分析圆锥摆小球的向心力来源
该错误在于对轨道半径认识不够
竖直方向:FN cosθ=mg
水平方向:
F合=mgtanθ=mω2 Lsinθ=mω2 htanθ
h
θ
O
R
ω
θ
ω
θ
m
m
mg
FN
F合
mg
FN
F合
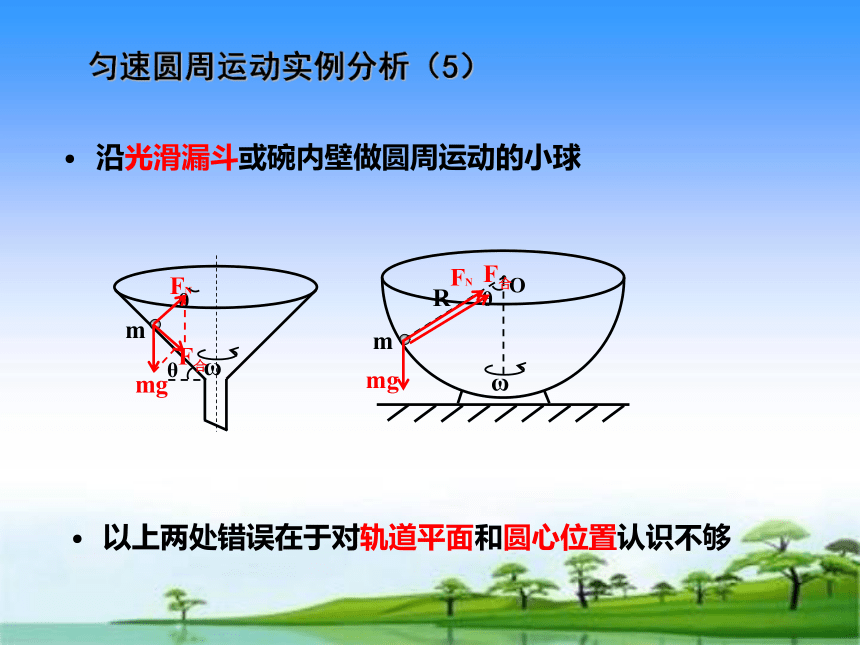
沿光滑漏斗或碗内壁做圆周运动的小球
匀速圆周运动实例分析(5)
以上两处错误在于对轨道平面和圆心位置认识不够
θ
O'
O
R
ω
θ
ω
θ
m
m
O
r
mg
FN
F合
mg
FN
F合
竖直方向:
FN cosθ=mg
水平方向:
F合=mg tanθ=mω2r
竖直方向:
FN cosθ=mg
水平方向:
F合=mg tanθ=mω2 R sinθ
沿光滑漏斗或碗内壁做圆周运动的小球
匀速圆周运动实例分析(5)
向心力特点总结:
⑴向心力是根据效果命名的力,并不是一种新的性质的力。
⑵来源:可以是重力、弹力、摩擦力单独提供的力,也可以是几个力的合力,还可以是某个力的分力。
物体做匀速圆周运动时,合力提供向心力。
(3)向心力不是实际受到的力,不能说受到向心力作用 ,只能说某力或某几力提供了向心力。
(4)向心力是变力,方向时刻变化。
向心力的大小如何确定?与哪些因素有关?
二、探究向心力大小与半径、角速度、质量的关系
探究方案一 感受向心力
1.实验原理:沙袋在水平面内做
匀速圆周运动,此时沙袋
所受的向心力近似等于 .
绳对沙袋的拉力
2.实验步骤
(1)质量和角速度不变,改变半径,比较向心力与 的关系.
(2)质量和半径不变,改变角速度,比较向心力与 的关系.
(3)角速度和半径不变,改变质量,比较向心力与______的关系.
3.实验结论:半径越 ,角速度越 ,质量越 ,向心力越大
半径
角速度
大
大
大
质量
探究方案二 用向心力演示器定量探究
1.实验原理
(1)相同角速度ω获取:
皮带套在相同半径的圆盘上,
(2)n倍数角速度ω获取:
皮带套在半径比为n:1的圆盘上,
(3)相同和不同转动半径r获取:长槽内外和短槽外
(4)向心力来源: 挡板对小球的压力
(5)向心力比值大小的记录:标尺8上露出的红白相间等分标记,可以粗略计算向心力的比值.
向心力演示器
2.实验探究
(1)Fn与m关系:r和ω相同,则m不同、相同圆盘. 、长内
(2)Fn与r关系:m和ω相同,则m相同、相同圆盘. 、长外
(3)Fn与ω关系:m和r相同,则m相同、不同圆盘. 、长内
3.实验结论:
半径和角速度一定,向心力大小与质量成 .
质量和角速度一定,向心力大小与半径成 .
质量和半径一定,向心力大小与 成正比.
正比
正比
角速度的平方
正比
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
ω1:ω2
r1:r2
m1:m2
F1:F2
实验一
1:1
1:1
1:2
1:2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
ω1:ω2
r1:r2
m1:m2
F1:F2
实验二
1:1
1:1
2:1
2:1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
ω1:ω2
r1:r2
m1:m2
F1:F2
实验三
1:1
1:1
1:1
1:1
1:2
1:4
1:3
1:9
向心力常见表达式:
?????????=????????2????
?
????????=????????2????
?
????????=????????????
?
????????=????4????2????2????
?
????????=?4????2????2????????
?
课堂训练
1.一个小球在细绳的拉力作用下,绕某固定点在水平面内作匀速圆周运动,空气阻力不计。小球在运动过程中不发生改变的物理量是( )
A.速度 B.角速度
C.加速度 D.向心力
B
2.如图,用向心力演示器探究向心力大小的表达式,已知小球在挡板A、B、C处做圆周运动的轨迹半径之比为1∶2∶1,在利用该装置做探究向心力与角速度之间的关系时,应让质量相同的小球分别放在______处,同时选择半径______的两个塔轮。
A.挡板A与挡板B,相同B.挡板A与挡板C,相同
C.挡板A与挡板C,不同D.挡板A与挡板B,不同
C
变速圆周运动和一般曲线运动的受力特点
仔细观察运动员掷链球时的动作,运动员使链球加速转动时,绳子牵引链球的方向并不与链球运动的方向垂直。也就是说,链球加速时,它所受的合力并不严格指向运动轨迹的圆心。
链球正在加速转动的情况
(1)圆心:O是链球运动轨迹的圆心,
(2)受力分析:F是绳对链球的拉力。
(3)向心力来源:F分解为两个相互垂直的分力:跟圆周相切
的分力F和指向圆心的分力F。
(4)动力学分析:
?F1与链球运动的速度同向,使得链球的速度越来越大;
?Fn指向圆心,提供链球做圆周运动所需的向心力,改变链球
速度的方向。
思考与讨论:当物体做圆周运动的线速度逐渐减小时,物体所受合力的方向与速度方向的夹角是大于90°还是小于90°呢?
大于90°
F
Fn
Ft
v0
Ft与物体运动的速度反向,使得物体的速度越来越小;Fn指向圆心,提供物体做圆周运动所需的向心力,改变物体速度的方向。
可以把这条曲线分割为许多很短的小段,质点在每小段的运动都可以看作圆周运动的一部分。只是不同位置对应的“圆周运动”的“圆心”和“半径”不同。
一般的曲线运动
(1)定义:运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般的曲线运动。
(2)研究方法:采用圆周运动的分析方法来处理。
匀速圆周运动与变速圆周运动的比较
例:双人花样滑冰运动中,女运动员被男运动员拉着离开冰面在空中做圆锥摆运动,若女运动员做圆锥摆运动时和竖直方向的夹角约为θ,女运动员的质量为m,转动过程中女运动员的重心做匀速圆周运动的半径为r,求:
(1)男运动员对女运动员的拉力大小。
(2)男运动员转动的角速度。
匀速圆周运动问题的解题策略
1.运动分析:确定圆周运动轨道平面,圆心和半径。
2.向心力来源分析:明确向心力是由什么力提供的。
3.选择合适的公式列式求解。
课堂小结
6.2 向心力
空中飞椅与人一起做匀速圆周运动的过程中,受到了哪些力?所受合力的方向有什么特点?
温故知新
什么是匀速圆周运动?
物体沿着圆周运动,且线速度的大小处处相等
匀速圆周运动的物体速度是否改变?
速度大小不变方向不断变化
速度变化
具有加速度
合外力不为零合外力有何特点?
观察分析
光滑水平桌面,一根细绳系住小球,小球做匀速圆周运动。
小球受几个力的作用?小球的合外力有何特点?
受力分析
结论:做匀速圆周运动的物体,合外力指向圆心,始终与速度V垂直。
向心力
1.定义:做匀速圆周运动的物体一定受到
一个指向圆心的合力,这个力叫做向心力。
2.方向:总指向圆心,与线速度垂直,方向不断变化。
3.效果:只改变速度方向,不改变速度大小。
轻绳栓一小球,在光滑水平面做匀速圆周运动。小球向心力的来源?
O
G
FN
F
向心力由小球受到的桌面支持力FN、小球的重力G、绳子的拉力F的合力提供。也可以说是细绳拉力提供向心力。
匀速圆周运动实例分析(1)
F向= F合= F
4.向心力来源
物体相对转盘静止,随盘做匀速圆周运动
F向= F合= f
由物块受到的重力、支持力、静摩擦力三个力的合力提供。即圆盘对木块的静摩擦力f
ω
O
G
FN
f
匀速圆周运动实例分析(2)
G
f
FN
ω
讨论:物块随着圆桶一起匀速转动时,物块的受力?物块向心力的来源?
物块做匀速圆周运动时,合力提供向心力,即桶对物块的支持力。
匀速圆周运动实例分析(3)
学科网
F向= F合= FN
如图:拉力和重力的合力提供物体做匀速圆周运动向心力。
O'
ω
O
θ
l
m
mg
F合
FT
匀速圆周运动实例分析(4)
竖直方向:FN cosθ=mg
水平方向:F合=mg tanθ=mω2 L
分析圆锥摆小球的向心力来源
该错误在于对轨道半径认识不够
竖直方向:FN cosθ=mg
水平方向:
F合=mgtanθ=mω2 Lsinθ=mω2 htanθ
h
θ
O
R
ω
θ
ω
θ
m
m
mg
FN
F合
mg
FN
F合
沿光滑漏斗或碗内壁做圆周运动的小球
匀速圆周运动实例分析(5)
以上两处错误在于对轨道平面和圆心位置认识不够
θ
O'
O
R
ω
θ
ω
θ
m
m
O
r
mg
FN
F合
mg
FN
F合
竖直方向:
FN cosθ=mg
水平方向:
F合=mg tanθ=mω2r
竖直方向:
FN cosθ=mg
水平方向:
F合=mg tanθ=mω2 R sinθ
沿光滑漏斗或碗内壁做圆周运动的小球
匀速圆周运动实例分析(5)
向心力特点总结:
⑴向心力是根据效果命名的力,并不是一种新的性质的力。
⑵来源:可以是重力、弹力、摩擦力单独提供的力,也可以是几个力的合力,还可以是某个力的分力。
物体做匀速圆周运动时,合力提供向心力。
(3)向心力不是实际受到的力,不能说受到向心力作用 ,只能说某力或某几力提供了向心力。
(4)向心力是变力,方向时刻变化。
向心力的大小如何确定?与哪些因素有关?
二、探究向心力大小与半径、角速度、质量的关系
探究方案一 感受向心力
1.实验原理:沙袋在水平面内做
匀速圆周运动,此时沙袋
所受的向心力近似等于 .
绳对沙袋的拉力
2.实验步骤
(1)质量和角速度不变,改变半径,比较向心力与 的关系.
(2)质量和半径不变,改变角速度,比较向心力与 的关系.
(3)角速度和半径不变,改变质量,比较向心力与______的关系.
3.实验结论:半径越 ,角速度越 ,质量越 ,向心力越大
半径
角速度
大
大
大
质量
探究方案二 用向心力演示器定量探究
1.实验原理
(1)相同角速度ω获取:
皮带套在相同半径的圆盘上,
(2)n倍数角速度ω获取:
皮带套在半径比为n:1的圆盘上,
(3)相同和不同转动半径r获取:长槽内外和短槽外
(4)向心力来源: 挡板对小球的压力
(5)向心力比值大小的记录:标尺8上露出的红白相间等分标记,可以粗略计算向心力的比值.
向心力演示器
2.实验探究
(1)Fn与m关系:r和ω相同,则m不同、相同圆盘. 、长内
(2)Fn与r关系:m和ω相同,则m相同、相同圆盘. 、长外
(3)Fn与ω关系:m和r相同,则m相同、不同圆盘. 、长内
3.实验结论:
半径和角速度一定,向心力大小与质量成 .
质量和角速度一定,向心力大小与半径成 .
质量和半径一定,向心力大小与 成正比.
正比
正比
角速度的平方
正比
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
ω1:ω2
r1:r2
m1:m2
F1:F2
实验一
1:1
1:1
1:2
1:2
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
ω1:ω2
r1:r2
m1:m2
F1:F2
实验二
1:1
1:1
2:1
2:1
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
ω1:ω2
r1:r2
m1:m2
F1:F2
实验三
1:1
1:1
1:1
1:1
1:2
1:4
1:3
1:9
向心力常见表达式:
?????????=????????2????
?
????????=????????2????
?
????????=????????????
?
????????=????4????2????2????
?
????????=?4????2????2????????
?
课堂训练
1.一个小球在细绳的拉力作用下,绕某固定点在水平面内作匀速圆周运动,空气阻力不计。小球在运动过程中不发生改变的物理量是( )
A.速度 B.角速度
C.加速度 D.向心力
B
2.如图,用向心力演示器探究向心力大小的表达式,已知小球在挡板A、B、C处做圆周运动的轨迹半径之比为1∶2∶1,在利用该装置做探究向心力与角速度之间的关系时,应让质量相同的小球分别放在______处,同时选择半径______的两个塔轮。
A.挡板A与挡板B,相同B.挡板A与挡板C,相同
C.挡板A与挡板C,不同D.挡板A与挡板B,不同
C
变速圆周运动和一般曲线运动的受力特点
仔细观察运动员掷链球时的动作,运动员使链球加速转动时,绳子牵引链球的方向并不与链球运动的方向垂直。也就是说,链球加速时,它所受的合力并不严格指向运动轨迹的圆心。
链球正在加速转动的情况
(1)圆心:O是链球运动轨迹的圆心,
(2)受力分析:F是绳对链球的拉力。
(3)向心力来源:F分解为两个相互垂直的分力:跟圆周相切
的分力F和指向圆心的分力F。
(4)动力学分析:
?F1与链球运动的速度同向,使得链球的速度越来越大;
?Fn指向圆心,提供链球做圆周运动所需的向心力,改变链球
速度的方向。
思考与讨论:当物体做圆周运动的线速度逐渐减小时,物体所受合力的方向与速度方向的夹角是大于90°还是小于90°呢?
大于90°
F
Fn
Ft
v0
Ft与物体运动的速度反向,使得物体的速度越来越小;Fn指向圆心,提供物体做圆周运动所需的向心力,改变物体速度的方向。
可以把这条曲线分割为许多很短的小段,质点在每小段的运动都可以看作圆周运动的一部分。只是不同位置对应的“圆周运动”的“圆心”和“半径”不同。
一般的曲线运动
(1)定义:运动轨迹既不是直线也不是圆周的曲线运动,可以称为一般的曲线运动。
(2)研究方法:采用圆周运动的分析方法来处理。
匀速圆周运动与变速圆周运动的比较
例:双人花样滑冰运动中,女运动员被男运动员拉着离开冰面在空中做圆锥摆运动,若女运动员做圆锥摆运动时和竖直方向的夹角约为θ,女运动员的质量为m,转动过程中女运动员的重心做匀速圆周运动的半径为r,求:
(1)男运动员对女运动员的拉力大小。
(2)男运动员转动的角速度。
匀速圆周运动问题的解题策略
1.运动分析:确定圆周运动轨道平面,圆心和半径。
2.向心力来源分析:明确向心力是由什么力提供的。
3.选择合适的公式列式求解。
课堂小结
