江苏省无锡市洛社高级中学2013届高三10月月考数学(文)试题
文档属性
| 名称 | 江苏省无锡市洛社高级中学2013届高三10月月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 255.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-15 21:31:49 | ||
图片预览

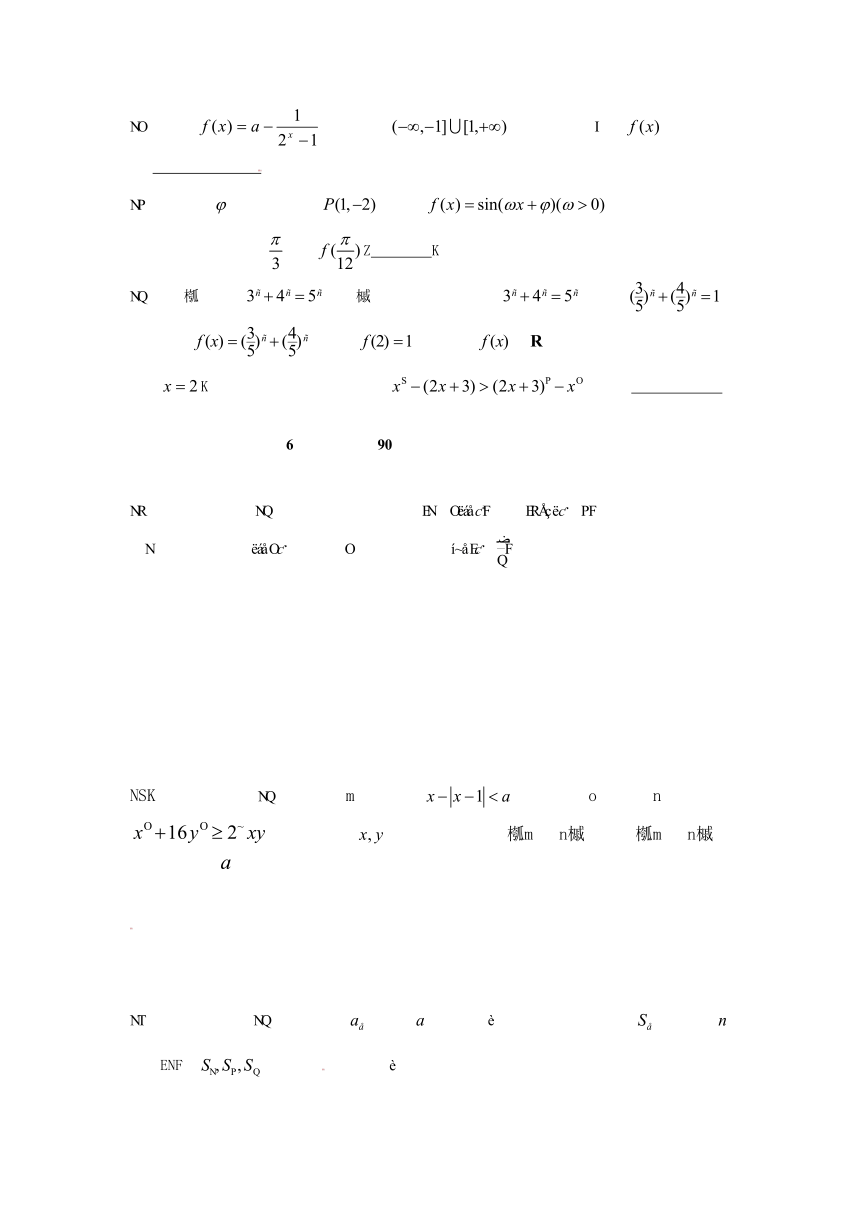


文档简介
一、填空题:(本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上.)
1.已知,是虚数单位,若,则的值是 ▲ .
2.数列中,前项和,,则的通项公式为 ▲ .
3.对于大于或等于2的自然数的3次方幂如下分解方式:;;…根据上述分解规律,若的分解式中最小的数是31,则的值为 ▲
4.设实数x,y满足约束条件,则目标函数z=2x+y的最大值为 ▲ .
5.已知非零向量a,b满足|a|=|a+b|=1,a与b夹角为120°,则向量b的模为 ▲ .
6.有3个兴趣小组,甲、乙两位同学各参加其中一个小组,且他们参加各个
兴趣小组是等可能的,则甲、乙两位同学参加同一个兴趣小组的概率为 ▲ .
7.右图是一个算法的流程图,最后输出的k= ▲ .
8、等差数列的公差,且,则数列前n项和取
最大值时 ▲
9. 某教师出了一份三道题的测试卷,每道题1分,全班得3分、2分、1分
和0分的学生所占比例分别为30%、50%、10%和10%,则全班学生的平均
分为 ▲ 分.
10.已知命题p: x∈R,+2x+3≥0,如果命题p是真命题,则实数a的取值范围是 ▲ .
11..在ABC中, a、b、c分别为内角A、B、C所对的边,且A =300 .现给出三个条件:①a=2; ②B = 450 ;③c=3b .试从中选出两个可以确定ABC的条件,并以此为依据求ABC的面积.(只需写出一个选定方案即可)你选择的条件是
(用序号填写);由此得到的ABC的面积为 .
12.已知是定义在上的奇函数, 则的值域为 ▲ 。
13.已知角的终边经过点,函数图象的相邻两条对称轴之间的距离等于,则= ▲ .
14.问题“求方程的解”有如下的思路:方程可变为,
考察函数可知,,且函数在上单调递减,∴原方程有唯一解.仿照此解法可得到不等式:的解是 ▲ .
二、解答题:本大题共6小题,共计90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)已知平面向量a=(1,2sinθ),b=(5cosθ,3).
(1)若a∥b,求sin2θ的值;(2)若a⊥b,求tan(θ+)的值.
16. (本小题满分14分)命题P:不等式的解集为R,命题Q:不等式对一切正数恒成立,若命题“P且Q”为假,“P或Q”为真,求实数的范围。
17、(本小题满分14分)已知﹛﹜是以为首项,q为公比的等比数列,为它的前项和(1)当成等差数列时,求q的值;
(2)当,,成等差数列时,求证:对任意自然数也成等差数列
18.(本小题满分16分)经市场调查,某商场的一种商品在过去的一个月内(以30天计)销售价格(元)与时间(天)的函数关系近似满足(为正常数),日销售量(件)与时间(天)的函数关系近似满足,且第25天的销售金额为13000元.
(1)求的值;
(2)试写出该商品的日销售金额关于时间的函数关系式;
(3)该商品的日销售金额的最小值是多少?.
19、(本小题满分16分)
已知数列中,且点在直线上。
(1)求数列的通项公式;
(2)若函数求函数的最小值;
(3)设表示数列的前项和。试问:是否存在关于的整式,使得
对于一切不小于2的自然数恒成立? 若存在,写出的解析式,并加以证明;若不存在,试说明理由。
20.(本小题满分16分)已知函数,其中e是自然数的底数,.
(1)当时,解不等式;
(2)当时,求正整数k的值,使方程在[k,k+1]上有解;
(3)若在[-1,1]上是单调增函数,求的取值范围.
高三数学(文科)第一次阶段性学情检测试卷
一、填空题:
二、解答题:
15.(本小题满分14分)
解:(1)因为a∥b,所以1×3-2sinθ×5cosθ=0, …………………3分
即5sin2θ-3=0,所以sin2θ=. …………………6分
(2)因为a⊥b,所以1×5cosθ+2sinθ×3=0. …………………8分
所以tanθ=-. …………………10分
所以tan(θ+)=eq \F(tanθ+tan,1-tanθtan)=. …………………14分
16(本小题满分14分)
解:P:令 …………………4分
Q: …………………8分
若P真Q假: ……………………………………10分
若P假Q真: ……………………………………12分
综上所述: ……………………………………14分
17. (本小题满分14分)
解:(1) 成等差数列
①当时这显然不成立 ………………… 2分
②当时,
…………………7分
(2)①当时显然成立 …………………9分
18、(本大题满分16分)
解:(1)由题意,得,即,解得…3分
(2)
= …………………8分
(3)①当时,因为,所以当时,有最小值12100 …11分
②当时,∵在上递减,∴当时, 有最小值12400 ………………14分
∵12100〈12400,∴当时,该商品的日销售金额取得最小值为12100 …16分
19、(本大题满分16分)
解:(1)由点P在直线上,
即,------------------------------------------2分
且,数列{}是以1为首项,1为公差的等差数列
,同样满足,所以---------------4分
(2)
---------------------6分
所以是单调递增,故的最小值是-----------------------10分
,n≥2------------------14分
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立----16分
20.(本大题满分16分)
⑴因为,所以不等式即为,
又因为,所以不等式可化为,
所以不等式的解集为.………………………………………4分
⑵当时, 方程即为,由于,所以不是方程的解,
所以原方程等价于,令,
因为对于恒成立,
所以在内是单调增函数,……………………………6分
又,, ,
所以方程有且只有1个实数根, 在区间 ,
所以整数的值为 1.……………………………………………8分
⑶,
①当时,,在上恒成立,当且仅当时
取等号,故符合要求;………………………………………………………10分
②当时,令,因为,
所以有两个不相等的实数根,,不妨设,
因此有极大值又有极小值.
若,因为,所以在内有极值点,
故在上不单调.………………………………………………………12分
若,可知,
因为的图象开口向下,要使在上单调,因为,
必须满足即所以.--------------------------14分
综上可知,的取值范围是.………………………………………16分
开始
k←1
S←0
S<20
k←k+2
S←S+k
Y
N
输出k
结束
(第7题)
1.已知,是虚数单位,若,则的值是 ▲ .
2.数列中,前项和,,则的通项公式为 ▲ .
3.对于大于或等于2的自然数的3次方幂如下分解方式:;;…根据上述分解规律,若的分解式中最小的数是31,则的值为 ▲
4.设实数x,y满足约束条件,则目标函数z=2x+y的最大值为 ▲ .
5.已知非零向量a,b满足|a|=|a+b|=1,a与b夹角为120°,则向量b的模为 ▲ .
6.有3个兴趣小组,甲、乙两位同学各参加其中一个小组,且他们参加各个
兴趣小组是等可能的,则甲、乙两位同学参加同一个兴趣小组的概率为 ▲ .
7.右图是一个算法的流程图,最后输出的k= ▲ .
8、等差数列的公差,且,则数列前n项和取
最大值时 ▲
9. 某教师出了一份三道题的测试卷,每道题1分,全班得3分、2分、1分
和0分的学生所占比例分别为30%、50%、10%和10%,则全班学生的平均
分为 ▲ 分.
10.已知命题p: x∈R,+2x+3≥0,如果命题p是真命题,则实数a的取值范围是 ▲ .
11..在ABC中, a、b、c分别为内角A、B、C所对的边,且A =300 .现给出三个条件:①a=2; ②B = 450 ;③c=3b .试从中选出两个可以确定ABC的条件,并以此为依据求ABC的面积.(只需写出一个选定方案即可)你选择的条件是
(用序号填写);由此得到的ABC的面积为 .
12.已知是定义在上的奇函数, 则的值域为 ▲ 。
13.已知角的终边经过点,函数图象的相邻两条对称轴之间的距离等于,则= ▲ .
14.问题“求方程的解”有如下的思路:方程可变为,
考察函数可知,,且函数在上单调递减,∴原方程有唯一解.仿照此解法可得到不等式:的解是 ▲ .
二、解答题:本大题共6小题,共计90分.请在答卷纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)已知平面向量a=(1,2sinθ),b=(5cosθ,3).
(1)若a∥b,求sin2θ的值;(2)若a⊥b,求tan(θ+)的值.
16. (本小题满分14分)命题P:不等式的解集为R,命题Q:不等式对一切正数恒成立,若命题“P且Q”为假,“P或Q”为真,求实数的范围。
17、(本小题满分14分)已知﹛﹜是以为首项,q为公比的等比数列,为它的前项和(1)当成等差数列时,求q的值;
(2)当,,成等差数列时,求证:对任意自然数也成等差数列
18.(本小题满分16分)经市场调查,某商场的一种商品在过去的一个月内(以30天计)销售价格(元)与时间(天)的函数关系近似满足(为正常数),日销售量(件)与时间(天)的函数关系近似满足,且第25天的销售金额为13000元.
(1)求的值;
(2)试写出该商品的日销售金额关于时间的函数关系式;
(3)该商品的日销售金额的最小值是多少?.
19、(本小题满分16分)
已知数列中,且点在直线上。
(1)求数列的通项公式;
(2)若函数求函数的最小值;
(3)设表示数列的前项和。试问:是否存在关于的整式,使得
对于一切不小于2的自然数恒成立? 若存在,写出的解析式,并加以证明;若不存在,试说明理由。
20.(本小题满分16分)已知函数,其中e是自然数的底数,.
(1)当时,解不等式;
(2)当时,求正整数k的值,使方程在[k,k+1]上有解;
(3)若在[-1,1]上是单调增函数,求的取值范围.
高三数学(文科)第一次阶段性学情检测试卷
一、填空题:
二、解答题:
15.(本小题满分14分)
解:(1)因为a∥b,所以1×3-2sinθ×5cosθ=0, …………………3分
即5sin2θ-3=0,所以sin2θ=. …………………6分
(2)因为a⊥b,所以1×5cosθ+2sinθ×3=0. …………………8分
所以tanθ=-. …………………10分
所以tan(θ+)=eq \F(tanθ+tan,1-tanθtan)=. …………………14分
16(本小题满分14分)
解:P:令 …………………4分
Q: …………………8分
若P真Q假: ……………………………………10分
若P假Q真: ……………………………………12分
综上所述: ……………………………………14分
17. (本小题满分14分)
解:(1) 成等差数列
①当时这显然不成立 ………………… 2分
②当时,
…………………7分
(2)①当时显然成立 …………………9分
18、(本大题满分16分)
解:(1)由题意,得,即,解得…3分
(2)
= …………………8分
(3)①当时,因为,所以当时,有最小值12100 …11分
②当时,∵在上递减,∴当时, 有最小值12400 ………………14分
∵12100〈12400,∴当时,该商品的日销售金额取得最小值为12100 …16分
19、(本大题满分16分)
解:(1)由点P在直线上,
即,------------------------------------------2分
且,数列{}是以1为首项,1为公差的等差数列
,同样满足,所以---------------4分
(2)
---------------------6分
所以是单调递增,故的最小值是-----------------------10分
,n≥2------------------14分
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立----16分
20.(本大题满分16分)
⑴因为,所以不等式即为,
又因为,所以不等式可化为,
所以不等式的解集为.………………………………………4分
⑵当时, 方程即为,由于,所以不是方程的解,
所以原方程等价于,令,
因为对于恒成立,
所以在内是单调增函数,……………………………6分
又,, ,
所以方程有且只有1个实数根, 在区间 ,
所以整数的值为 1.……………………………………………8分
⑶,
①当时,,在上恒成立,当且仅当时
取等号,故符合要求;………………………………………………………10分
②当时,令,因为,
所以有两个不相等的实数根,,不妨设,
因此有极大值又有极小值.
若,因为,所以在内有极值点,
故在上不单调.………………………………………………………12分
若,可知,
因为的图象开口向下,要使在上单调,因为,
必须满足即所以.--------------------------14分
综上可知,的取值范围是.………………………………………16分
开始
k←1
S←0
S<20
k←k+2
S←S+k
Y
N
输出k
结束
(第7题)
同课章节目录
