1.2.4绝对值
图片预览





文档简介
(共19张PPT)
1.2.4
绝对值
绝对值
细心,踏实,方法!
思考:-8与8是相反数,把它们在数轴上表示出来,它们有什么相同之处和不同之处?
-8与8在数轴上所表示的点到原点的距离是8个单位长度,它们的符号不同。我们把这个距离8叫做+8和-8的绝对值。
想一想,互为相反数的两个数的绝对值有什么关系?你能给大家举几对吗?通过观察、比较、归纳能得出什么结论?
活动2:理解绝对值的概念
-8
8
0
8
8
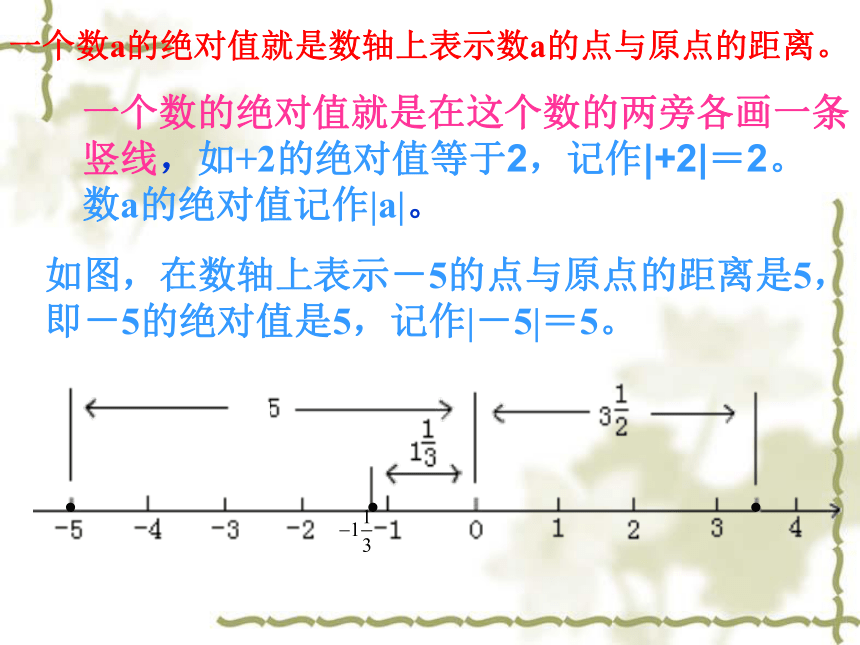
一个数a的绝对值就是数轴上表示数a的点与原点的距离。
一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作|+2|=2。
数a的绝对值记作|a|。
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5。
做一做
写出下列各数的绝对值:
解:
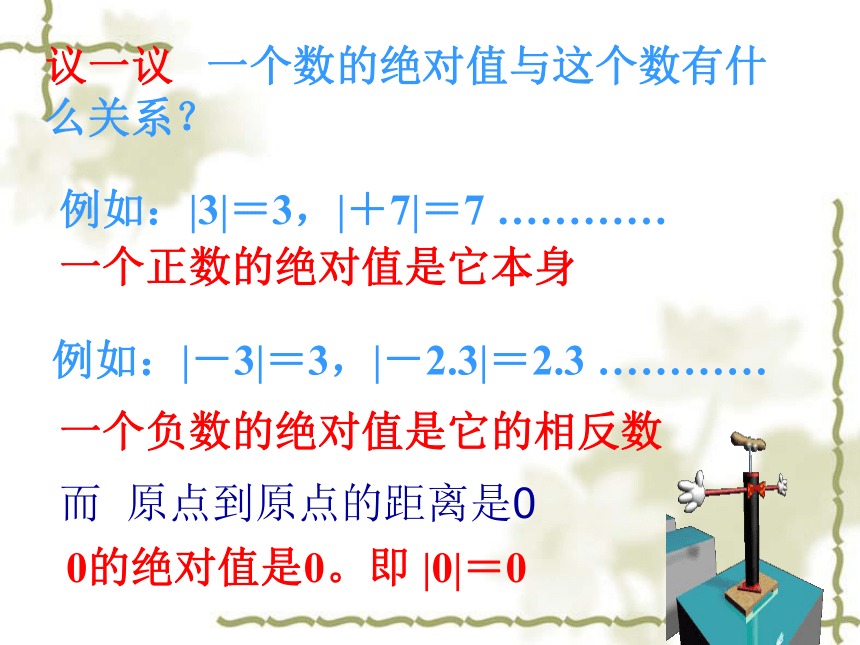
议一议 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0。即 |0|=0
而 原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
做一做
写出下列各数的绝对值:
解:
想一想
1) 绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
判断:
(1)一个数的绝对值是 2 ,则这数是2 。 (2)|5|=|-5|。 (3)|-0.3|=|0.3|。 (4)|3|>0。 (5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。 (8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。 (10)互为相反数的两个数的绝对值相等。
课堂小结
1,数轴上表示数a的点与原点的距离叫做数a的绝对值。
3,(1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
2,
2、已知有理数a在数轴上对应的点如图所示:
则|a| =________
4、如果a 的相反数是-0.74,那么|a| =______
3. 如果一个数的绝对值等于3.25 ,则这个数是___
5. 如果|x|=2,则x=______.
a
0
2、知道一个数的绝对值,求这个数
⑴.绝对值是+3.1的数是_________,绝对值小于2的整数是_________.
⑵.若│x│=5,则x=______,若│x-3│=0,则x=_________.
⑶.若│x│=│-7│,则x=___,若│x-1│=2,则x=_________.
3、非负性 │a│≥0
(1)、若│x-2│+ │y-3│=0,求 x·y= _________
4、有条件的绝对值化简
课前小测
1、绝对值等于3的数有 _________个,它们是_________。
2、若│x│=4,则x=______,若│x-5│=0,则x=_________.
3、绝对值小于5但大于2的整数是_________.
4、(1)、若│x-3│+ │y+5│=0,求 x+y= _________
5、已知|x|=3,|y|=4,求x+y的值。
思考:
对于正数、0、和负数这三类数,
它们之间有什么大小关系?
两个负数之间如何比较大小?
在数轴上表示下列各数,并比较 它们的大小: - 1.5 , - 3 , - 1 , - 5
求出(1)中各数的绝对值,并比较它们的大小
你发现了什么?
做一做
两个负数比较大小,绝对值 大的反而小。
例题:比较下列各对数的大小
(1) -(-1)和-(+2)
(2) 和
(3)-(-0.03)和
课后再探索
1、已知|x|=3,|y|=4,求x+y的值。
2、正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下表:
问题:
(1)指出哪个排球的质量好一些(即重量最接近规定质量)?
(2)如果对两个排球作上述检查,检查的结果分别为p和q,请利用学过的绝对值的知识指出这两个排球中哪个质量好一些?
+15 -10 +30 -20 -40
1.2.4
绝对值
绝对值
细心,踏实,方法!
思考:-8与8是相反数,把它们在数轴上表示出来,它们有什么相同之处和不同之处?
-8与8在数轴上所表示的点到原点的距离是8个单位长度,它们的符号不同。我们把这个距离8叫做+8和-8的绝对值。
想一想,互为相反数的两个数的绝对值有什么关系?你能给大家举几对吗?通过观察、比较、归纳能得出什么结论?
活动2:理解绝对值的概念
-8
8
0
8
8
一个数a的绝对值就是数轴上表示数a的点与原点的距离。
一个数的绝对值就是在这个数的两旁各画一条竖线,如+2的绝对值等于2,记作|+2|=2。
数a的绝对值记作|a|。
如图,在数轴上表示-5的点与原点的距离是5,即-5的绝对值是5,记作|-5|=5。
做一做
写出下列各数的绝对值:
解:
议一议 一个数的绝对值与这个数有什么关系?
例如:|3|=3,|+7|=7 …………
一个正数的绝对值是它本身
例如:|-3|=3,|-2.3|=2.3 …………
一个负数的绝对值是它的相反数
0的绝对值是0。即 |0|=0
而 原点到原点的距离是0
因为正数可用a>0表示,负数可用a<0表示,所以上述三条可表述成: (1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
做一做
写出下列各数的绝对值:
解:
想一想
1) 绝对值是7的数有几个?各是什么?有
没有绝对值是-2的数?
答:绝对值是7的数有两个,各是7与-7。
没有绝对值是-2的数。
绝对值是0的数有几个?各是什么?
答:绝对值是0的数有一个,就是0。
3)绝对值小于3的整数一共有多少个?
答:绝对值小于3的整数一共有5个,
它们分别是-2,-1,0,1,2。
判断:
(1)一个数的绝对值是 2 ,则这数是2 。 (2)|5|=|-5|。 (3)|-0.3|=|0.3|。 (4)|3|>0。 (5)|-1.4|>0。
(6)有理数的绝对值一定是正数。
(7)若a=b,则|a|=|b|。 (8)若|a|=|b|,则a=b。
(9)若|a|=-a,则a必为负数。 (10)互为相反数的两个数的绝对值相等。
课堂小结
1,数轴上表示数a的点与原点的距离叫做数a的绝对值。
3,(1)如果a>0,那么|a|=a (2)如果a<0,那么|a|=-a (3)如果a=0,那么|a|=0
2,
2、已知有理数a在数轴上对应的点如图所示:
则|a| =________
4、如果a 的相反数是-0.74,那么|a| =______
3. 如果一个数的绝对值等于3.25 ,则这个数是___
5. 如果|x|=2,则x=______.
a
0
2、知道一个数的绝对值,求这个数
⑴.绝对值是+3.1的数是_________,绝对值小于2的整数是_________.
⑵.若│x│=5,则x=______,若│x-3│=0,则x=_________.
⑶.若│x│=│-7│,则x=___,若│x-1│=2,则x=_________.
3、非负性 │a│≥0
(1)、若│x-2│+ │y-3│=0,求 x·y= _________
4、有条件的绝对值化简
课前小测
1、绝对值等于3的数有 _________个,它们是_________。
2、若│x│=4,则x=______,若│x-5│=0,则x=_________.
3、绝对值小于5但大于2的整数是_________.
4、(1)、若│x-3│+ │y+5│=0,求 x+y= _________
5、已知|x|=3,|y|=4,求x+y的值。
思考:
对于正数、0、和负数这三类数,
它们之间有什么大小关系?
两个负数之间如何比较大小?
在数轴上表示下列各数,并比较 它们的大小: - 1.5 , - 3 , - 1 , - 5
求出(1)中各数的绝对值,并比较它们的大小
你发现了什么?
做一做
两个负数比较大小,绝对值 大的反而小。
例题:比较下列各对数的大小
(1) -(-1)和-(+2)
(2) 和
(3)-(-0.03)和
课后再探索
1、已知|x|=3,|y|=4,求x+y的值。
2、正式排球比赛对所用的排球重量是有严格规定的,现检查5个排球的重量,超过规定重量的克数记作正数,不足规定重量的克数记作负数,检查结果如下表:
问题:
(1)指出哪个排球的质量好一些(即重量最接近规定质量)?
(2)如果对两个排球作上述检查,检查的结果分别为p和q,请利用学过的绝对值的知识指出这两个排球中哪个质量好一些?
+15 -10 +30 -20 -40
