湘教版七年级下册数学 第1章二元一次方程组达标测试卷(word版含答案)
文档属性
| 名称 | 湘教版七年级下册数学 第1章二元一次方程组达标测试卷(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 49.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览


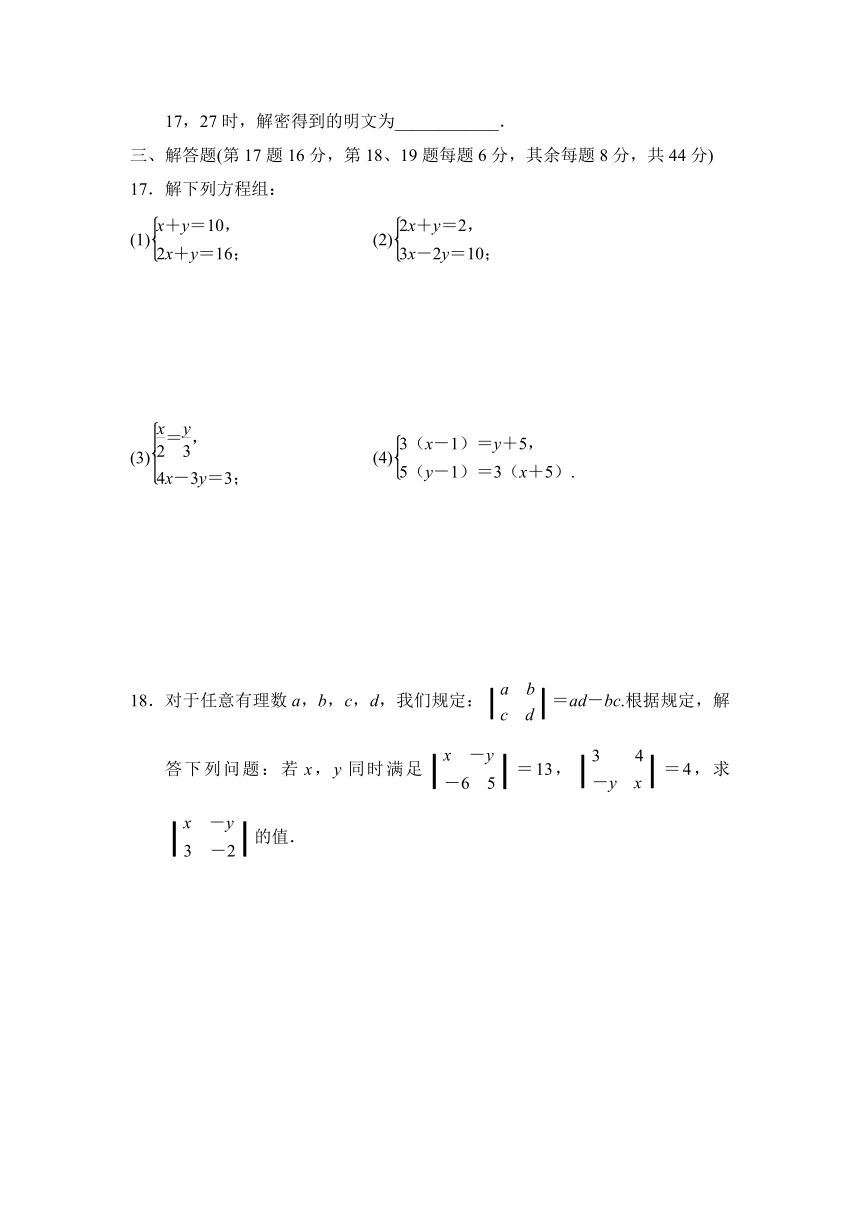

文档简介
第1章达标测试卷
一、选择题(每题3分,共24分)
1.下列各方程组中,是二元一次方程组的是( )
A. B. C. D.
2.用加减法解方程组时,较简便的方法是( )
A.①×4-②×3,消去x B.①×4+②×3,消去x
C.②×2+①,消去y D.②×2-①,消去y
3.方程组的解为则m,n的值分别为( )
A.1,2 B.1,3 C.5,1 D.2,4
4.如果关于x,y的方程组与的解相同,那么a+b的值为( )
A.-1 B.1 C.2 D.0
5.已知方程组的解满足x-y=m-1,则m的值为( )
A.-1 B.-2
C.1 D.2
6.已知二元一次方程组则(x+y)(x-y)的值是( )
A.15 B.-5 C.5 D.-15
7.小明到商店购买“五四青年”活动奖品,购买20支铅笔和10本笔记本共需110元,但购买30支铅笔和5本笔记本只需85元.设每支铅笔x元,每本笔记本y元,则可列方程组为( )
A. B.
C. D.
8.我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )
A. B.
C. D.
二、填空题(每题4分,共32分)
9.若5xm-1+5yn-3=-1是关于x,y的二元一次方程,则m+n=________.
10.已知二元一次方程x+3y=14,请写出该方程的一个整数解:______________.
11.若-7xay3与x2ya+b是同类项,则b=________.
12.已知关于x,y的二元一次方程组则x-y的值是__________.
13.若与都是方程ax-by=3的解,则a=________,b=________.
14.已知关于x,y的二元一次方程组的解为则关于a,b的二元一次方程组的解是________.
15.有大、小两种货车,2辆大货车与1辆小货车一次可以运货7吨,1辆大货车与2辆小货车一次可以运货5吨,则1辆大货车与1辆小货车一次可以运货________吨.
16.为确保信息安全,信息需要加密传输,发送方由明文对应密文(加密),接收方由密文对应明文(解密).已知加密规则:明文x,y,z对应密文2x+3y,3x+4y,3z.例如:明文1,2,3对应密文8,11,9.当接收方收到密文12,17,27时,解密得到的明文为____________.
三、解答题(第17题16分,第18、19题每题6分,其余每题8分,共44分)
17.解下列方程组:
(1) (2)
(3) (4)
18.对于任意有理数a,b,c,d,我们规定:=ad-bc.根据规定,解答下列问题:若x,y同时满足=13,=4,求的值.
19.某景点的门票价格如下表:
购票人数 1~50 51~100 100以上
每张门票价格/元 12 10 8
某校七年级一、二两班计划去游览该景点,其中一班人数少于50人,二班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付1 118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)求七年级一班、二班的学生人数;
(2)团体购票与单独购票相比较,两个班各节省了多少钱?
20.某厂共有104名生产工人,每名工人每天可生产螺栓20个或螺母25个,一个螺栓与两个螺母配成一套.
(1)每天安排多少名工人生产螺栓,多少名工人生产螺母,才能使每天生产出来的产品配套?
(2)若每套利润20元,求每天的利润.
21.某商场计划用9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为甲型号每台1 500元,乙型号每台2 100元,丙型号每台2 500元.
(1)若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲型号电视机可获利150元,销售一台乙型号电视机可获利200元,销售一台丙型号电视机可获利250元,在同时购进两种不同型号电视机的方案中,选择哪一种进货方案,获得的利润最大?
答案
一、1.D 2.D
3.C 点拨:根据题意,得2+n=3,
解得n=1,所以2x+y=4+1=5.
所以m=5.
4.B
5.D 点拨:
②-①,得x-y=1,
因为方程组的解满足x-y=m-1,所以m-1=1,解得m=2.
6.B 【点拨】
①+②,得3x+3y=15,
所以x+y=5,
①-②,得x-y=-1,
所以(x+y)(x-y)=5× (-1)=-5.
故选B.
7.B 8.A
二、9.6
10.(答案不唯一)
11.1
12.1 【点拨】
①+②,得3x-3y=3,
即3(x-y)=3,
故x-y=1.
13.-3;-3 点拨:根据题意得所以
14. 点拨:因为关于x,y的二元一次方程组的解为所以由关于a,b的二元一次方程组可得解得
15.4 点拨:设1辆大货车一次可以运货x吨,1辆小货车一次可以运货y吨,根据题意得
(①+②)÷3,得x+y=4.
16.3,2,9
三、17.解:(1)
由①得,y=10-x,③
把③代入②,得2x+10-x=16,
解得x=6.
把x=6代入③,得y=4,
则原方程组的解为
(2)
①×2,得4x+2y=4,③
②+③,得7x=14,解得x=2.
把x=2代入①,得4+y=2,
解得y=-2.
则原方程组的解为
(3)把原方程组整理,得
把①代入②,得y-3y=3,
解得y=-9.
把y=-9代入①,得x=-6.
则原方程组的解为
(4)把原方程组整理,得
①-②,得4y=28,
解得y=7.
把y=7代入①,得x=5.
则原方程组的解为
18.解:根据题意得
①×2+②×3,得19x= 38,
解得x=2,
把x=2代入②,得6+4y =4,
解得y=-,
所以==
-2×2-3×=-5.
19.解:(1)设两个班的人数之和为w人.由题意知w>50.当50<w≤100时,10w=816,解得w=81.6.
因为81.6不是整数,所以不合题意.
当w>100时,设七年级一班有x人,七年级二班有y人,由题意,
得解得
答:七年级一班有49人,七年级二班有53人.
(2)七年级一班节省的费用为(12-8)×49=196(元),
七年级二班节省的费用为(10-8)×53=106(元).
20.解:(1)设每天安排x名工人生产螺栓,y名工人生产螺母,才能使每天生产出来的产品配套,
根据题意,得解得
答:每天安排40名工人生产螺栓,64名工人生产螺母,才能使每天生产出来的产品配套.
(2)40×20×20=16 000(元).
答:每天的利润为16 000元.
21.解:(1)①设购进甲型号电视机x台,乙型号电视机y台,则
解得
②设购进甲型号电视机m台,丙型号电视机z台,
则解得
③设购进乙型号电视机n台,丙型号电视机k台,
则解得(不合题意,舍去).
综上,商场的进货方案有两种:①购进25台甲型号电视机和25台乙型号电视机;②购进35台甲型号电视机和15台丙型号电视机.
(2)25×150+25×200=8 750(元),
35×150+15×250=9 000(元).
因为8 750<9 000,
所以购进甲型号电视机35台,丙型号电视机15台,获得的利润最大.
一、选择题(每题3分,共24分)
1.下列各方程组中,是二元一次方程组的是( )
A. B. C. D.
2.用加减法解方程组时,较简便的方法是( )
A.①×4-②×3,消去x B.①×4+②×3,消去x
C.②×2+①,消去y D.②×2-①,消去y
3.方程组的解为则m,n的值分别为( )
A.1,2 B.1,3 C.5,1 D.2,4
4.如果关于x,y的方程组与的解相同,那么a+b的值为( )
A.-1 B.1 C.2 D.0
5.已知方程组的解满足x-y=m-1,则m的值为( )
A.-1 B.-2
C.1 D.2
6.已知二元一次方程组则(x+y)(x-y)的值是( )
A.15 B.-5 C.5 D.-15
7.小明到商店购买“五四青年”活动奖品,购买20支铅笔和10本笔记本共需110元,但购买30支铅笔和5本笔记本只需85元.设每支铅笔x元,每本笔记本y元,则可列方程组为( )
A. B.
C. D.
8.我国古代数学名著《张邱建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗.今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是:现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒、醑酒各几斗?如果设清酒x斗,醑酒y斗,那么可列方程组为( )
A. B.
C. D.
二、填空题(每题4分,共32分)
9.若5xm-1+5yn-3=-1是关于x,y的二元一次方程,则m+n=________.
10.已知二元一次方程x+3y=14,请写出该方程的一个整数解:______________.
11.若-7xay3与x2ya+b是同类项,则b=________.
12.已知关于x,y的二元一次方程组则x-y的值是__________.
13.若与都是方程ax-by=3的解,则a=________,b=________.
14.已知关于x,y的二元一次方程组的解为则关于a,b的二元一次方程组的解是________.
15.有大、小两种货车,2辆大货车与1辆小货车一次可以运货7吨,1辆大货车与2辆小货车一次可以运货5吨,则1辆大货车与1辆小货车一次可以运货________吨.
16.为确保信息安全,信息需要加密传输,发送方由明文对应密文(加密),接收方由密文对应明文(解密).已知加密规则:明文x,y,z对应密文2x+3y,3x+4y,3z.例如:明文1,2,3对应密文8,11,9.当接收方收到密文12,17,27时,解密得到的明文为____________.
三、解答题(第17题16分,第18、19题每题6分,其余每题8分,共44分)
17.解下列方程组:
(1) (2)
(3) (4)
18.对于任意有理数a,b,c,d,我们规定:=ad-bc.根据规定,解答下列问题:若x,y同时满足=13,=4,求的值.
19.某景点的门票价格如下表:
购票人数 1~50 51~100 100以上
每张门票价格/元 12 10 8
某校七年级一、二两班计划去游览该景点,其中一班人数少于50人,二班人数多于50人且少于100人.如果两班都以班为单位单独购票,则一共支付1 118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)求七年级一班、二班的学生人数;
(2)团体购票与单独购票相比较,两个班各节省了多少钱?
20.某厂共有104名生产工人,每名工人每天可生产螺栓20个或螺母25个,一个螺栓与两个螺母配成一套.
(1)每天安排多少名工人生产螺栓,多少名工人生产螺母,才能使每天生产出来的产品配套?
(2)若每套利润20元,求每天的利润.
21.某商场计划用9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为甲型号每台1 500元,乙型号每台2 100元,丙型号每台2 500元.
(1)若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲型号电视机可获利150元,销售一台乙型号电视机可获利200元,销售一台丙型号电视机可获利250元,在同时购进两种不同型号电视机的方案中,选择哪一种进货方案,获得的利润最大?
答案
一、1.D 2.D
3.C 点拨:根据题意,得2+n=3,
解得n=1,所以2x+y=4+1=5.
所以m=5.
4.B
5.D 点拨:
②-①,得x-y=1,
因为方程组的解满足x-y=m-1,所以m-1=1,解得m=2.
6.B 【点拨】
①+②,得3x+3y=15,
所以x+y=5,
①-②,得x-y=-1,
所以(x+y)(x-y)=5× (-1)=-5.
故选B.
7.B 8.A
二、9.6
10.(答案不唯一)
11.1
12.1 【点拨】
①+②,得3x-3y=3,
即3(x-y)=3,
故x-y=1.
13.-3;-3 点拨:根据题意得所以
14. 点拨:因为关于x,y的二元一次方程组的解为所以由关于a,b的二元一次方程组可得解得
15.4 点拨:设1辆大货车一次可以运货x吨,1辆小货车一次可以运货y吨,根据题意得
(①+②)÷3,得x+y=4.
16.3,2,9
三、17.解:(1)
由①得,y=10-x,③
把③代入②,得2x+10-x=16,
解得x=6.
把x=6代入③,得y=4,
则原方程组的解为
(2)
①×2,得4x+2y=4,③
②+③,得7x=14,解得x=2.
把x=2代入①,得4+y=2,
解得y=-2.
则原方程组的解为
(3)把原方程组整理,得
把①代入②,得y-3y=3,
解得y=-9.
把y=-9代入①,得x=-6.
则原方程组的解为
(4)把原方程组整理,得
①-②,得4y=28,
解得y=7.
把y=7代入①,得x=5.
则原方程组的解为
18.解:根据题意得
①×2+②×3,得19x= 38,
解得x=2,
把x=2代入②,得6+4y =4,
解得y=-,
所以==
-2×2-3×=-5.
19.解:(1)设两个班的人数之和为w人.由题意知w>50.当50<w≤100时,10w=816,解得w=81.6.
因为81.6不是整数,所以不合题意.
当w>100时,设七年级一班有x人,七年级二班有y人,由题意,
得解得
答:七年级一班有49人,七年级二班有53人.
(2)七年级一班节省的费用为(12-8)×49=196(元),
七年级二班节省的费用为(10-8)×53=106(元).
20.解:(1)设每天安排x名工人生产螺栓,y名工人生产螺母,才能使每天生产出来的产品配套,
根据题意,得解得
答:每天安排40名工人生产螺栓,64名工人生产螺母,才能使每天生产出来的产品配套.
(2)40×20×20=16 000(元).
答:每天的利润为16 000元.
21.解:(1)①设购进甲型号电视机x台,乙型号电视机y台,则
解得
②设购进甲型号电视机m台,丙型号电视机z台,
则解得
③设购进乙型号电视机n台,丙型号电视机k台,
则解得(不合题意,舍去).
综上,商场的进货方案有两种:①购进25台甲型号电视机和25台乙型号电视机;②购进35台甲型号电视机和15台丙型号电视机.
(2)25×150+25×200=8 750(元),
35×150+15×250=9 000(元).
因为8 750<9 000,
所以购进甲型号电视机35台,丙型号电视机15台,获得的利润最大.
