湘教版七年级下册数学 第4章相交线与平行线达标测试卷(word版含答案)
文档属性
| 名称 | 湘教版七年级下册数学 第4章相交线与平行线达标测试卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 142.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 10:42:43 | ||
图片预览


文档简介
第4章达标测试卷
一、选择题(每题3分,共24分)
1.下列图形中,能将其中一个三角形平移得到另一个三角形的是( )
2.a,b,c是同一平面内任意三条直线,它们的交点可能有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.都不对
3. “玉兔”在月球表面行走的动力主要来自于太阳光能,要使接收太阳光能最多,就要使光线垂直照射在太阳光板上.现在太阳光如图照射,那么使得接收太阳光能最多时,太阳光板绕支点A逆时针最小旋转( )
A.46° B.44° C.36° D.54°
4.下列语句叙述正确的有( )
①如果两个角有公共顶点且没有公共边,那么这两个角是对顶角;
②如果两个角相等,那么这两个角是对顶角;
③连接两点的线段的长度叫做两点间的距离;
④直线外一点到这条直线的垂线段叫做这点到直线的距离.
A.0个 B.1个 C.2个 D.3个
5.如图,对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4
C.∠3=∠4 D.∠1+∠4=180°
6.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为( )
A.30° B.60°
C.80° D.120°
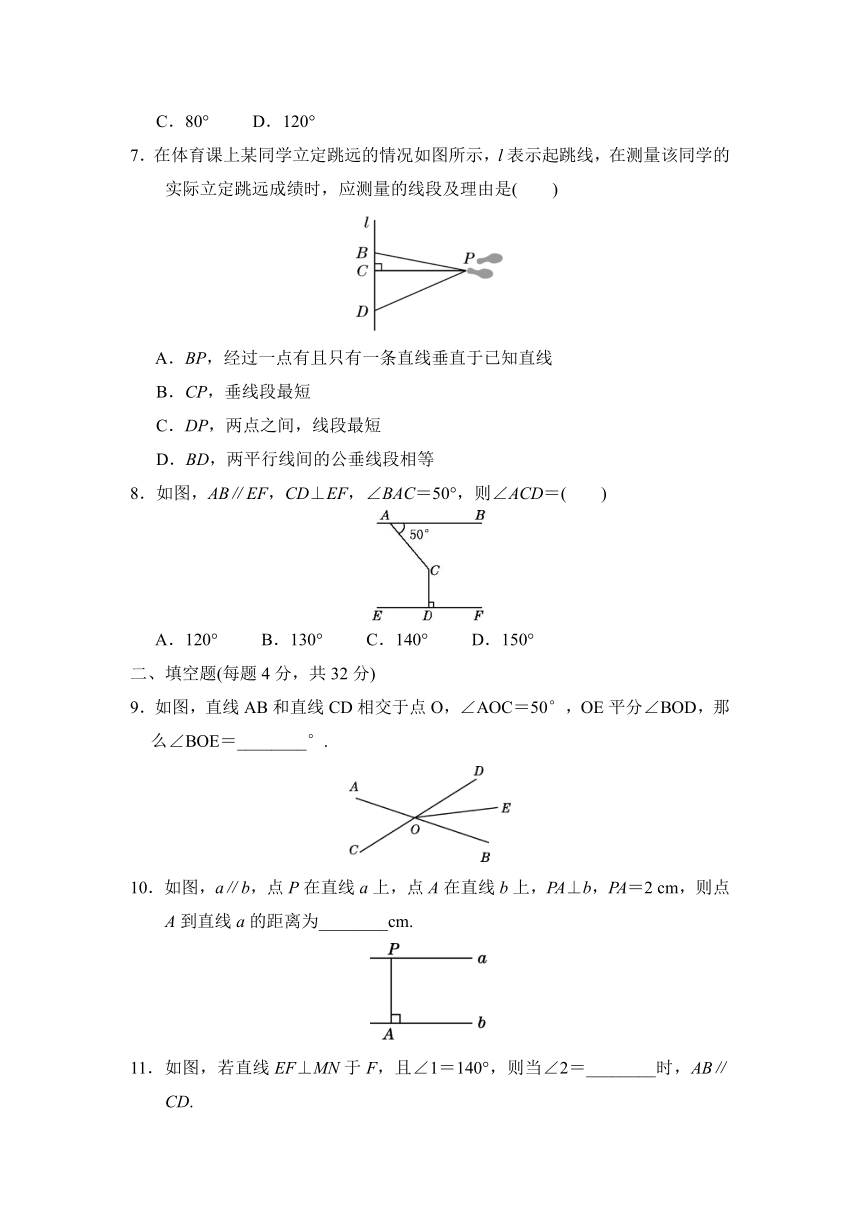
7.在体育课上某同学立定跳远的情况如图所示,l表示起跳线,在测量该同学的实际立定跳远成绩时,应测量的线段及理由是( )
A.BP,经过一点有且只有一条直线垂直于已知直线
B.CP,垂线段最短
C.DP,两点之间,线段最短
D.BD,两平行线间的公垂线段相等
8.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )
A.120° B.130° C.140° D.150°
二、填空题(每题4分,共32分)
9.如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE=________°.
10.如图,a∥b,点P在直线a上,点A在直线b上,PA⊥b,PA=2 cm,则点A到直线a的距离为________cm.
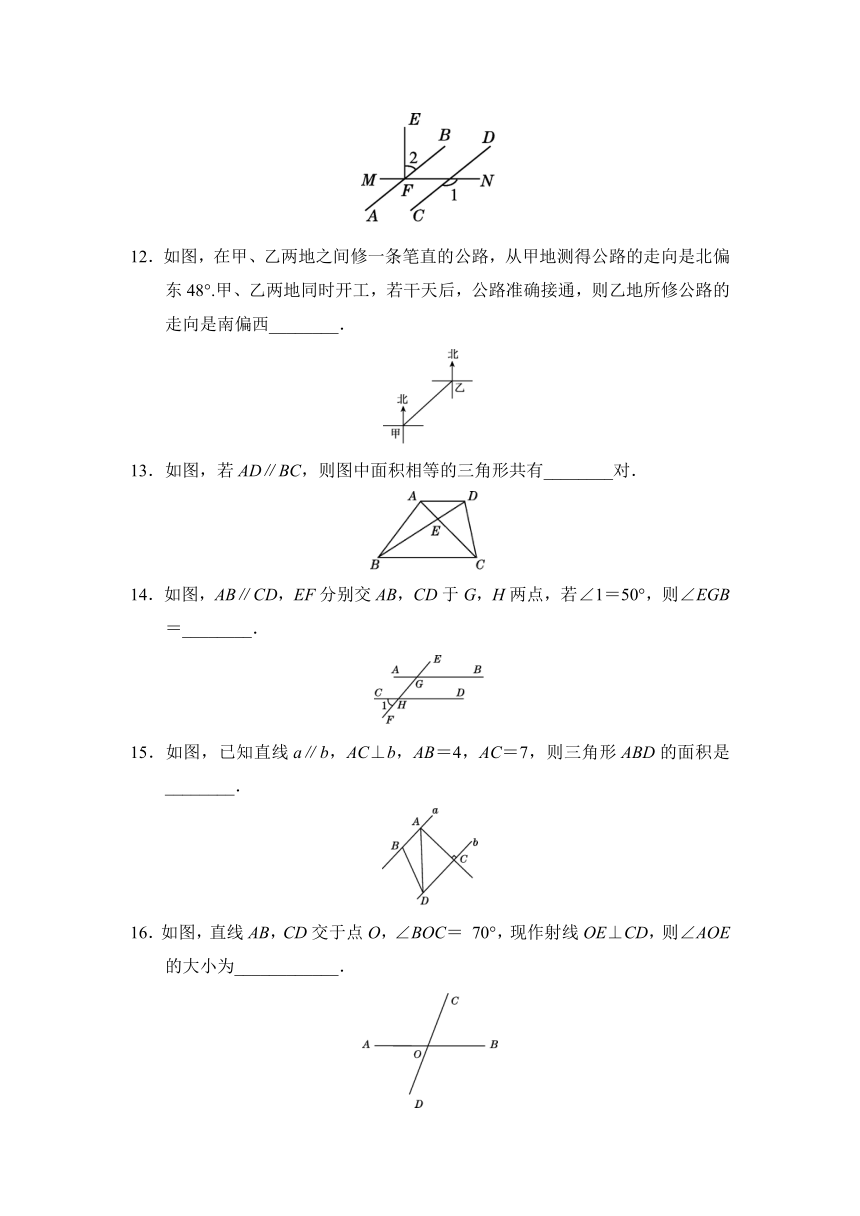
11.如图,若直线EF⊥MN于F,且∠1=140°,则当∠2=________时,AB∥CD.
12.如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西________.
13.如图,若AD∥BC,则图中面积相等的三角形共有________对.
14.如图,AB∥CD,EF分别交AB,CD于G,H两点,若∠1=50°,则∠EGB=________.
15.如图,已知直线a∥b,AC⊥b,AB=4,AC=7,则三角形ABD的面积是________.
16.如图,直线AB,CD交于点O,∠BOC= 70°,现作射线OE⊥CD,则∠AOE的大小为____________.
三、解答题(17题8分,其余每题9分,共44分)
17.如图,O是直线AB上一点,∠AOC=50°,OD是∠BOC的平分线,OE⊥OC于点O.求∠DOE的度数.
18.如图,CD⊥AB,GF⊥AB,垂足分别为D,F,E为AC上一点,∠AED=∠ACB,试说明:∠1=∠2.
19.如图,将周长为18 cm的三角形ABC沿BC方向平移得到三角形DEF.如果四边形ABFD的周长是21 cm,求平移的距离.
20.O为直线DA上一点,OB⊥OF,OE是∠AOB的平分线.
(1)如图①,若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数(用含α的式子表示);
(3)若∠AOB=α,0°<α<90°,请在图②中画出射线OF,使得(2)中的结论仍然成立.
21.问题情境:如图①,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的解题思路:如图②,过P作PE∥AB,通过平行线的性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A,B两点外侧运动(点P与点A,B,O三点不重合),请你直接写出∠CPD,∠α,∠β之间的数量关系.
答案
一、1.A
2.B 点拨:三条直线两两平行,有0个交点;三条直线交于一点,有1个交点;两条直线平行与第三条直线相交,有2个交点;三条直线两两相交,不交于同一点,有3个交点,故选B.本题考查了相交线,分类讨论是解题的关键,注意不要漏掉任何一种情况.
3.B 4.B 5.D 6.A 7.B 8.C
二、9.25
10.2 点拨:因为a∥b,PA⊥b,PA=2 cm,所以AP⊥a,所以点A到直线a的距离=PA=2 cm.
11.50° 点拨:如图,因为AB∥CD,所以∠3=∠4(两直线平行,同位角相等).又因为∠1+∠3=180°,∠1=140°,所以∠3=∠4=40°.
因为EF⊥MN,所以∠2+∠4=90°,所以∠2=50°.
12.48° 点拨:如图,因为AC∥BD,∠1=48°,所以∠2=∠1=48°,根据方向角的概念可知,乙地所修公路的走向是南偏西48°.
13.3 点拨:面积相等的三角形共有3对,分别是三角形ABC和三角形BCD,三角形ABD和三角形ACD,三角形ABE和三角形CDE.
14.50° 点拨:因为AB∥CD,所以∠1=∠AGF.因为∠AGF与∠EGB是对顶角,所以∠EGB=∠AGF=∠1=50°.
15.14
16.20°或160° 【点拨】因为OE⊥DC,
所以∠DOE=90°.
因为∠AOD=∠BOC,∠BOC=70°,
所以∠AOD=70°.
①当OE在DC的左侧时,
∠AOE=∠DOE-∠AOD=90°-70°=20°;
②当OE在DC的右侧时,
∠AOE=∠DOE+∠AOD=90°+70°=160°.
综上,∠AOE=20°或160°.
三、17.解:因为O是直线AB上一点,∠AOC=50°,
所以∠BOC=180°-∠AOC=130°.
因为OD是∠BOC的平分线,
所以∠COD=∠BOC.
所以∠COD=65°.
因为OE⊥OC于点O,
所以∠COE=90°.
所以∠DOE=∠COE-∠COD=25°.
18.解:因为CD⊥AB,GF⊥AB,
所以CD∥GF,
所以∠2=∠DCB.
因为∠AED=∠ACB,
所以DE∥BC,
所以∠1=∠DCB,
所以∠1=∠2.
19.解:因为三角形DEF是由三角形ABC沿BC方向平移得到的,所以AD=CF,AC=DF.
所以四边形ABFD的周长为AD+AB+BF+DF=AD+AB+BC+AC+CF=2AD+18=21,
所以2AD=3,
解得AD=1.5.
答:平移的距离为1.5 cm.
20.解:(1)因为∠AOB=130°,OE是∠AOB的平分线,
所以∠AOE=∠AOB=×130°=65°.
因为OB⊥OF,所以∠BOF=90°,
所以∠AOF=∠AOB-∠BOF=130°-90°=40°.
所以∠EOF=∠AOE-∠AOF=65°-40°=25°.
(2)因为∠AOB=α,90°<α<180°,OE是∠AOB的平分线,
所以∠AOE=α.
因为∠BOF=90°,
所以∠AOF=α-90°,
所以∠EOF=∠AOE-∠AOF=α-(α-90°)=90°-α.
(3)如图,因为∠AOB=α,0°<α<90°,OE是∠AOB的平分线,
所以∠BOE=∠AOE=α.
因为∠BOF=90°,
所以∠EOF=∠BOF-∠BOE=90°-α.
21.解:(1)∠CPD=∠α+∠β,
理由如下:如图①,过P作PE∥AD交CD于E,
因为AD∥BC,所以AD∥PE∥BC.
所以∠α=∠DPE,∠β=∠CPE.
所以∠CPD=∠DPE+∠CPE=∠α+∠β.
(2)当点P在线段BA的延长线上时,如图②.
∠CPD=∠β-∠α.
当点P在线段AB的延长线上时,如图③.
∠CPD=∠α-∠β.
一、选择题(每题3分,共24分)
1.下列图形中,能将其中一个三角形平移得到另一个三角形的是( )
2.a,b,c是同一平面内任意三条直线,它们的交点可能有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.都不对
3. “玉兔”在月球表面行走的动力主要来自于太阳光能,要使接收太阳光能最多,就要使光线垂直照射在太阳光板上.现在太阳光如图照射,那么使得接收太阳光能最多时,太阳光板绕支点A逆时针最小旋转( )
A.46° B.44° C.36° D.54°
4.下列语句叙述正确的有( )
①如果两个角有公共顶点且没有公共边,那么这两个角是对顶角;
②如果两个角相等,那么这两个角是对顶角;
③连接两点的线段的长度叫做两点间的距离;
④直线外一点到这条直线的垂线段叫做这点到直线的距离.
A.0个 B.1个 C.2个 D.3个
5.如图,对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠1=∠2 B.∠2=∠4
C.∠3=∠4 D.∠1+∠4=180°
6.如图,AD是∠EAC的平分线,AD∥BC,∠B=30°,则∠C的度数为( )
A.30° B.60°
C.80° D.120°
7.在体育课上某同学立定跳远的情况如图所示,l表示起跳线,在测量该同学的实际立定跳远成绩时,应测量的线段及理由是( )
A.BP,经过一点有且只有一条直线垂直于已知直线
B.CP,垂线段最短
C.DP,两点之间,线段最短
D.BD,两平行线间的公垂线段相等
8.如图,AB∥EF,CD⊥EF,∠BAC=50°,则∠ACD=( )
A.120° B.130° C.140° D.150°
二、填空题(每题4分,共32分)
9.如图,直线AB和直线CD相交于点O,∠AOC=50°,OE平分∠BOD,那么∠BOE=________°.
10.如图,a∥b,点P在直线a上,点A在直线b上,PA⊥b,PA=2 cm,则点A到直线a的距离为________cm.
11.如图,若直线EF⊥MN于F,且∠1=140°,则当∠2=________时,AB∥CD.
12.如图,在甲、乙两地之间修一条笔直的公路,从甲地测得公路的走向是北偏东48°.甲、乙两地同时开工,若干天后,公路准确接通,则乙地所修公路的走向是南偏西________.
13.如图,若AD∥BC,则图中面积相等的三角形共有________对.
14.如图,AB∥CD,EF分别交AB,CD于G,H两点,若∠1=50°,则∠EGB=________.
15.如图,已知直线a∥b,AC⊥b,AB=4,AC=7,则三角形ABD的面积是________.
16.如图,直线AB,CD交于点O,∠BOC= 70°,现作射线OE⊥CD,则∠AOE的大小为____________.
三、解答题(17题8分,其余每题9分,共44分)
17.如图,O是直线AB上一点,∠AOC=50°,OD是∠BOC的平分线,OE⊥OC于点O.求∠DOE的度数.
18.如图,CD⊥AB,GF⊥AB,垂足分别为D,F,E为AC上一点,∠AED=∠ACB,试说明:∠1=∠2.
19.如图,将周长为18 cm的三角形ABC沿BC方向平移得到三角形DEF.如果四边形ABFD的周长是21 cm,求平移的距离.
20.O为直线DA上一点,OB⊥OF,OE是∠AOB的平分线.
(1)如图①,若∠AOB=130°,求∠EOF的度数;
(2)若∠AOB=α,90°<α<180°,求∠EOF的度数(用含α的式子表示);
(3)若∠AOB=α,0°<α<90°,请在图②中画出射线OF,使得(2)中的结论仍然成立.
21.问题情境:如图①,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的解题思路:如图②,过P作PE∥AB,通过平行线的性质,可得∠APC=50°+60°=110°.
问题迁移:
(1)如图③,AD∥BC,点P在射线OM上运动,当点P在A,B两点之间运动时,∠ADP=∠α,∠BCP=∠β.∠CPD,∠α,∠β之间有何数量关系?请说明理由;
(2)在(1)的条件下,如果点P在A,B两点外侧运动(点P与点A,B,O三点不重合),请你直接写出∠CPD,∠α,∠β之间的数量关系.
答案
一、1.A
2.B 点拨:三条直线两两平行,有0个交点;三条直线交于一点,有1个交点;两条直线平行与第三条直线相交,有2个交点;三条直线两两相交,不交于同一点,有3个交点,故选B.本题考查了相交线,分类讨论是解题的关键,注意不要漏掉任何一种情况.
3.B 4.B 5.D 6.A 7.B 8.C
二、9.25
10.2 点拨:因为a∥b,PA⊥b,PA=2 cm,所以AP⊥a,所以点A到直线a的距离=PA=2 cm.
11.50° 点拨:如图,因为AB∥CD,所以∠3=∠4(两直线平行,同位角相等).又因为∠1+∠3=180°,∠1=140°,所以∠3=∠4=40°.
因为EF⊥MN,所以∠2+∠4=90°,所以∠2=50°.
12.48° 点拨:如图,因为AC∥BD,∠1=48°,所以∠2=∠1=48°,根据方向角的概念可知,乙地所修公路的走向是南偏西48°.
13.3 点拨:面积相等的三角形共有3对,分别是三角形ABC和三角形BCD,三角形ABD和三角形ACD,三角形ABE和三角形CDE.
14.50° 点拨:因为AB∥CD,所以∠1=∠AGF.因为∠AGF与∠EGB是对顶角,所以∠EGB=∠AGF=∠1=50°.
15.14
16.20°或160° 【点拨】因为OE⊥DC,
所以∠DOE=90°.
因为∠AOD=∠BOC,∠BOC=70°,
所以∠AOD=70°.
①当OE在DC的左侧时,
∠AOE=∠DOE-∠AOD=90°-70°=20°;
②当OE在DC的右侧时,
∠AOE=∠DOE+∠AOD=90°+70°=160°.
综上,∠AOE=20°或160°.
三、17.解:因为O是直线AB上一点,∠AOC=50°,
所以∠BOC=180°-∠AOC=130°.
因为OD是∠BOC的平分线,
所以∠COD=∠BOC.
所以∠COD=65°.
因为OE⊥OC于点O,
所以∠COE=90°.
所以∠DOE=∠COE-∠COD=25°.
18.解:因为CD⊥AB,GF⊥AB,
所以CD∥GF,
所以∠2=∠DCB.
因为∠AED=∠ACB,
所以DE∥BC,
所以∠1=∠DCB,
所以∠1=∠2.
19.解:因为三角形DEF是由三角形ABC沿BC方向平移得到的,所以AD=CF,AC=DF.
所以四边形ABFD的周长为AD+AB+BF+DF=AD+AB+BC+AC+CF=2AD+18=21,
所以2AD=3,
解得AD=1.5.
答:平移的距离为1.5 cm.
20.解:(1)因为∠AOB=130°,OE是∠AOB的平分线,
所以∠AOE=∠AOB=×130°=65°.
因为OB⊥OF,所以∠BOF=90°,
所以∠AOF=∠AOB-∠BOF=130°-90°=40°.
所以∠EOF=∠AOE-∠AOF=65°-40°=25°.
(2)因为∠AOB=α,90°<α<180°,OE是∠AOB的平分线,
所以∠AOE=α.
因为∠BOF=90°,
所以∠AOF=α-90°,
所以∠EOF=∠AOE-∠AOF=α-(α-90°)=90°-α.
(3)如图,因为∠AOB=α,0°<α<90°,OE是∠AOB的平分线,
所以∠BOE=∠AOE=α.
因为∠BOF=90°,
所以∠EOF=∠BOF-∠BOE=90°-α.
21.解:(1)∠CPD=∠α+∠β,
理由如下:如图①,过P作PE∥AD交CD于E,
因为AD∥BC,所以AD∥PE∥BC.
所以∠α=∠DPE,∠β=∠CPE.
所以∠CPD=∠DPE+∠CPE=∠α+∠β.
(2)当点P在线段BA的延长线上时,如图②.
∠CPD=∠β-∠α.
当点P在线段AB的延长线上时,如图③.
∠CPD=∠α-∠β.
