教科版高中物理必修1《匀变速直线运动位移与时间的关系》参考课件3(42张PPT)
文档属性
| 名称 | 教科版高中物理必修1《匀变速直线运动位移与时间的关系》参考课件3(42张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 880.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-05 09:55:27 | ||
图片预览









文档简介
(共42张PPT)
第六节
匀变速直线运动位移与时间的关系
课标定位:
应用:
1.运用匀变速直线运动的v-t图像解决有关位移问题.
2.运用公式x=v0t+ at2解决有关问题.
理解:
1.利用极限思想解决物理问题的科学思维方法.
2.公式x=v0t+ at2的意义和导出过程.
认识:
1.匀速直线运动的位移与v-t图像中矩形面积的对应关系.
2.匀变速直线运动的位移与v-t图像中四边形面积的对应关系.
第六节
核心要点突破
课堂互动讲练
课前自主学案
课标定位
课前自主学案
一、匀变速直线运动的位移
位移公式x=____________.
1.公式中x、v0、a均是_______,应用公式解题前应先根据正方向明确它们的正、负值.
2.当v0=0时,x=______,表示初速度为零的匀加速直线运动的_______与时间的关系.
3.当a=0时,x=v0t,表示_________运动的位移与时间的关系.
矢量
位移
匀速直线
二、位移—时间图像(x-t图像)
1.图像的作法
以横轴表示______,纵轴表示______.根据实际数据选取单位,选定标度,描出数据点,用平滑曲线连接各点得x-t图像.
2.图线的意义
表示的是物体做直线运动的______随_______变化的规律,而不是质点的运动轨迹.
时间
位移
位移
时间
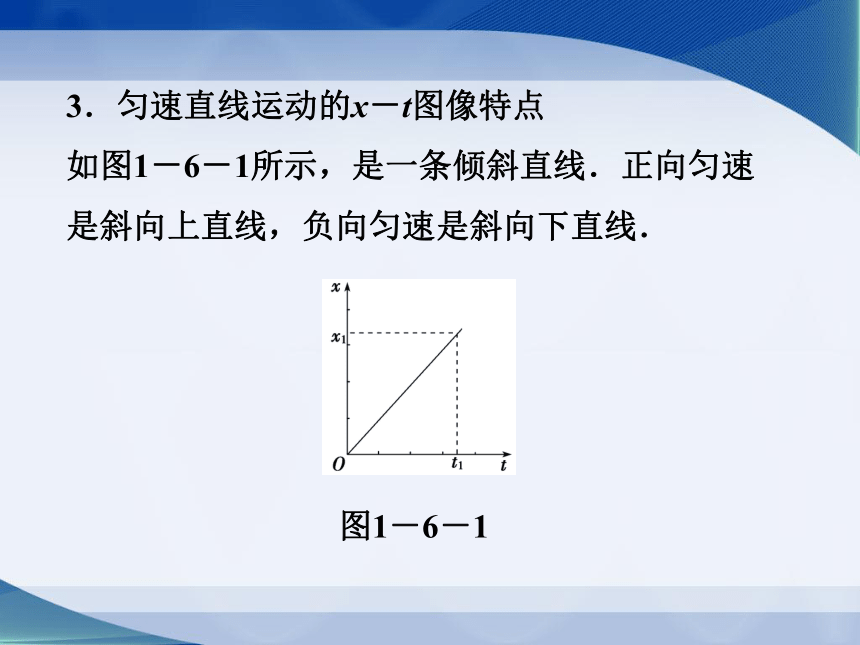
3.匀速直线运动的x-t图像特点
如图1-6-1所示,是一条倾斜直线.正向匀速是斜向上直线,负向匀速是斜向下直线.
图1-6-1
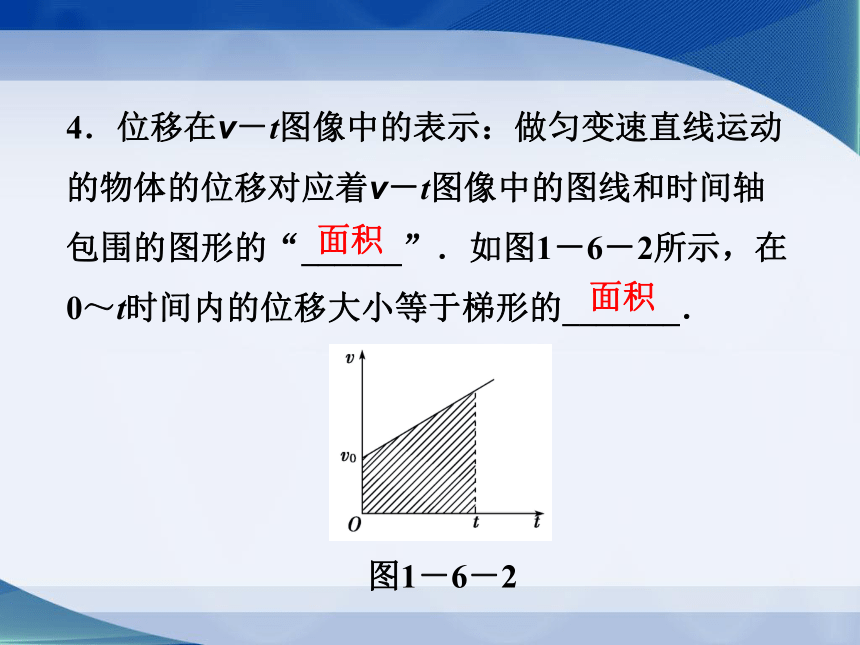
4.位移在v-t图像中的表示:做匀变速直线运动的物体的位移对应着v-t图像中的图线和时间轴包围的图形的“______”.如图1-6-2所示,在0~t时间内的位移大小等于梯形的_______.
面积
图1-6-2
面积
核心要点突破
一、对位移公式的进一步理解
1.反映了位移随时间的变化规律.
2.因为v0、a、x均为矢量,使用公式时应先规定正方向.一般以v0的方向为正方向.
若a与v0同向,则a取正值;
若a与v0反向,则a取负值;
若位移计算结果为正值,说明这段时间内位移的方向为正;
若位移计算结果为负值,说明这段时间内位移的方向为负.
即时应用?(即时突破,小试牛刀)
1.两物体都做匀变速直线运动,在给定的时间间隔内( )
A.加速度大的,其位移一定也大
B.初速度大的,其位移一定也大
C.末速度大的,其位移一定也大
D.平均速度大的,其位移一定也大
此推论常有两方面的应用:一是用以判断物体是否做匀变速直线运动;二是用以求加速度.
特别提醒:
(1)以上推论只适用于匀变速直线运动,其他性质的运动不能套用推论式来处理问题.
(2)推论式xⅡ-xⅠ=aT2常在实验中根据打出的纸带求物体的加速度.
即时应用?(即时突破,小试牛刀)
2.汽车由静止开始做匀加速直线运动,速度达到v时立即做匀减速直线运动,最后停止,运动的全部时间为t,则汽车通过的全部位移为( )
三、对位移—时间图像的理解
1.位移—时间图像(x-t图像)
在平面直角坐标系中,用横轴表示时间t,用纵轴表示位移x,如图1-6-3所示,根据给出(或测定)的数据,作出几个点的坐标,用直线将几个点连起来,则这条直线就表示了物体的运动特点.
图1-6-3
(2)若物体做匀速直线运动,则x-t图像是一条倾斜的直线,直线的斜率表示物体的速度.斜率的大小表示速度的大小,斜率的正、负表示物体的运动方向,如图1-6-3中的a、b所示.
(3)若x-t图像为平行于时间轴的直线,表明物体处于静止状态.如图1-6-3中的c所示.
图1-6-3
(4)纵截距表示运动物体的初始位置,图1-6-3中所示a、b物体分别是从原点、原点正方向x2处开始运动的.
(5)图线的交点表示相遇,如图1-6-3所示中的交点表示a、b、c三个物体在t1时刻在距原点正方向x1处相遇.
图1-6-3
特别提醒:
(1)x-t图像只能用来描述直线运动,图像弯曲,是质点速度变化的原因.
(2)x-t图像表示的是位移x随时间t变化的情况,绝不是物体运动的轨迹.
即时应用?(即时突破,小试牛刀)
3.某物体的位移与时间图像如图1-6-4所示,则下列叙述正确的是( )
A.物体运行的轨迹是抛物线
B.物体运行的时间为8 s
C.物体运动所能达到的最大位
移为80 m
D.在t=4 s时刻,物体的瞬时速度为零
图1-6-4
解析:选BCD.因为位移随时间的变化关系曲线并非为物体运动的轨迹.由图像可知,在0~4 s内物体沿正方向前进80 m,非匀速;4 s~8 s内物体沿与原来相反的方向运动至原点.在t=4 s时,图线上该点处切线的斜率为零,故此时速度为零.由以上分析知A错,B、C、D均正确.
课堂互动讲练
位移公式的理解及应用
一赛车进入直道后开始做匀加速运动,教练员测得在前2 s内经过的位移为52 m,随后3 s内经过的位移为123 m,之后还能加速2 s,求:
(1)赛车刚进入直道时的速度和加速度;
(2)赛车这一次在直道上加速的位移.
例1
【思路点拨】 题目中已知了时间、位移,利用位移与时间的关系列方程,可求得初速度和加速度.
【答案】 (1)20 m/s 6 m/s2 (2)287 m
变式训练1 汽车以2 m/s2的加速度由静止开始运动,求5 s内汽车的位移和第5 s内汽车的位移.
答案:25 m 9 m
位移图像的理解及应用
一辆汽车做直线运动的x-t图像如图1-6-5所示,请分析:
(1)以每5 s为时间间隔,求出各时间段内的平均速度;
(2)根据所得平均速度分析
这辆汽车做什么运动.
例2
图1-6-5
【思路点拨】 要求某一段内物体运动的平均速度,需先找出相应的位移和所用时间.根据x-t图像判断物体的运动情况,应根据图像斜率的变化分析,在x-t图像中,斜率表示了物体运动的速度.若斜率不变,则物体做匀速直线运动,若斜率发生变化,物体就做变速运动.
【答案】
(1)各时间段内的平均速度均为4 m/s
(2)匀速直线运动
【方法总结】 x-t图像反映了不同时刻质点的位移,图线的斜率表示速度的大小.斜率的正、负表示运动方向.
变式训练2 图1-6-6所示是A、B两质点做直线运动的位移—时间图像,由图可知( )
A.A物体做匀速直线运动
B.B物体做曲线运动
C.t0内A、B两物体的位移相等
D.t0内A、B两物体的路程相等
图1-6-6
解析:选ACD.由图像知,A质点的位移随时间均匀增加,故A做匀速直线运动.B质点的位移不随时间均匀变化,所以B做变速直线运动.A、B两质点的位移都随着时间的增加而增大,A、B均做单方向直线运动,所以t0时间内,A、B的位移相等,路程相等.
v-t图像的理解及应用
某一做直线运动的物体的v-t图像如图1-6-7所示,根据图像求:
(1)物体距出发点的最远距离.
(2)前4 s物体的位移.
(3)前4 s内通过的路程.
例3
图1-6-7
【思路点拨】 解答本题应注意以下三点:
(1)v-t图像与t轴所围的“面积”表示物体位移大小.
(2)“面积”在t轴之上表示位移是正值,在下表示位移是负值.
(3)物体通过的路程为t轴上、下“面积”绝对值的和.
【答案】 (1)6 m (2)5 m (3)7 m
变式训练3 有一质点从t=0开始,由原点沿着x轴正方向出发,其速度—时间图像如图1-6-8所示,下列说法正确的是( )
A.t=1 s,质点离原点的距离最大
B.t=2 s,质点离原点的距离最大
C.t=2 s,质点回到原点
D.t=4 s,质点回到原点
图1-6-8
解析:选BD.前2 s内,物体一直向正方向运动,后2 s向反方向运动,故2 s末物体离原点最远,A错、B对;由图像的面积等于位移可知,前2 s物体向前运动了5 m,后2 s又返回了5 m,故4 s末物体又回到出发的原点,C错,D对.
第六节
匀变速直线运动位移与时间的关系
课标定位:
应用:
1.运用匀变速直线运动的v-t图像解决有关位移问题.
2.运用公式x=v0t+ at2解决有关问题.
理解:
1.利用极限思想解决物理问题的科学思维方法.
2.公式x=v0t+ at2的意义和导出过程.
认识:
1.匀速直线运动的位移与v-t图像中矩形面积的对应关系.
2.匀变速直线运动的位移与v-t图像中四边形面积的对应关系.
第六节
核心要点突破
课堂互动讲练
课前自主学案
课标定位
课前自主学案
一、匀变速直线运动的位移
位移公式x=____________.
1.公式中x、v0、a均是_______,应用公式解题前应先根据正方向明确它们的正、负值.
2.当v0=0时,x=______,表示初速度为零的匀加速直线运动的_______与时间的关系.
3.当a=0时,x=v0t,表示_________运动的位移与时间的关系.
矢量
位移
匀速直线
二、位移—时间图像(x-t图像)
1.图像的作法
以横轴表示______,纵轴表示______.根据实际数据选取单位,选定标度,描出数据点,用平滑曲线连接各点得x-t图像.
2.图线的意义
表示的是物体做直线运动的______随_______变化的规律,而不是质点的运动轨迹.
时间
位移
位移
时间
3.匀速直线运动的x-t图像特点
如图1-6-1所示,是一条倾斜直线.正向匀速是斜向上直线,负向匀速是斜向下直线.
图1-6-1
4.位移在v-t图像中的表示:做匀变速直线运动的物体的位移对应着v-t图像中的图线和时间轴包围的图形的“______”.如图1-6-2所示,在0~t时间内的位移大小等于梯形的_______.
面积
图1-6-2
面积
核心要点突破
一、对位移公式的进一步理解
1.反映了位移随时间的变化规律.
2.因为v0、a、x均为矢量,使用公式时应先规定正方向.一般以v0的方向为正方向.
若a与v0同向,则a取正值;
若a与v0反向,则a取负值;
若位移计算结果为正值,说明这段时间内位移的方向为正;
若位移计算结果为负值,说明这段时间内位移的方向为负.
即时应用?(即时突破,小试牛刀)
1.两物体都做匀变速直线运动,在给定的时间间隔内( )
A.加速度大的,其位移一定也大
B.初速度大的,其位移一定也大
C.末速度大的,其位移一定也大
D.平均速度大的,其位移一定也大
此推论常有两方面的应用:一是用以判断物体是否做匀变速直线运动;二是用以求加速度.
特别提醒:
(1)以上推论只适用于匀变速直线运动,其他性质的运动不能套用推论式来处理问题.
(2)推论式xⅡ-xⅠ=aT2常在实验中根据打出的纸带求物体的加速度.
即时应用?(即时突破,小试牛刀)
2.汽车由静止开始做匀加速直线运动,速度达到v时立即做匀减速直线运动,最后停止,运动的全部时间为t,则汽车通过的全部位移为( )
三、对位移—时间图像的理解
1.位移—时间图像(x-t图像)
在平面直角坐标系中,用横轴表示时间t,用纵轴表示位移x,如图1-6-3所示,根据给出(或测定)的数据,作出几个点的坐标,用直线将几个点连起来,则这条直线就表示了物体的运动特点.
图1-6-3
(2)若物体做匀速直线运动,则x-t图像是一条倾斜的直线,直线的斜率表示物体的速度.斜率的大小表示速度的大小,斜率的正、负表示物体的运动方向,如图1-6-3中的a、b所示.
(3)若x-t图像为平行于时间轴的直线,表明物体处于静止状态.如图1-6-3中的c所示.
图1-6-3
(4)纵截距表示运动物体的初始位置,图1-6-3中所示a、b物体分别是从原点、原点正方向x2处开始运动的.
(5)图线的交点表示相遇,如图1-6-3所示中的交点表示a、b、c三个物体在t1时刻在距原点正方向x1处相遇.
图1-6-3
特别提醒:
(1)x-t图像只能用来描述直线运动,图像弯曲,是质点速度变化的原因.
(2)x-t图像表示的是位移x随时间t变化的情况,绝不是物体运动的轨迹.
即时应用?(即时突破,小试牛刀)
3.某物体的位移与时间图像如图1-6-4所示,则下列叙述正确的是( )
A.物体运行的轨迹是抛物线
B.物体运行的时间为8 s
C.物体运动所能达到的最大位
移为80 m
D.在t=4 s时刻,物体的瞬时速度为零
图1-6-4
解析:选BCD.因为位移随时间的变化关系曲线并非为物体运动的轨迹.由图像可知,在0~4 s内物体沿正方向前进80 m,非匀速;4 s~8 s内物体沿与原来相反的方向运动至原点.在t=4 s时,图线上该点处切线的斜率为零,故此时速度为零.由以上分析知A错,B、C、D均正确.
课堂互动讲练
位移公式的理解及应用
一赛车进入直道后开始做匀加速运动,教练员测得在前2 s内经过的位移为52 m,随后3 s内经过的位移为123 m,之后还能加速2 s,求:
(1)赛车刚进入直道时的速度和加速度;
(2)赛车这一次在直道上加速的位移.
例1
【思路点拨】 题目中已知了时间、位移,利用位移与时间的关系列方程,可求得初速度和加速度.
【答案】 (1)20 m/s 6 m/s2 (2)287 m
变式训练1 汽车以2 m/s2的加速度由静止开始运动,求5 s内汽车的位移和第5 s内汽车的位移.
答案:25 m 9 m
位移图像的理解及应用
一辆汽车做直线运动的x-t图像如图1-6-5所示,请分析:
(1)以每5 s为时间间隔,求出各时间段内的平均速度;
(2)根据所得平均速度分析
这辆汽车做什么运动.
例2
图1-6-5
【思路点拨】 要求某一段内物体运动的平均速度,需先找出相应的位移和所用时间.根据x-t图像判断物体的运动情况,应根据图像斜率的变化分析,在x-t图像中,斜率表示了物体运动的速度.若斜率不变,则物体做匀速直线运动,若斜率发生变化,物体就做变速运动.
【答案】
(1)各时间段内的平均速度均为4 m/s
(2)匀速直线运动
【方法总结】 x-t图像反映了不同时刻质点的位移,图线的斜率表示速度的大小.斜率的正、负表示运动方向.
变式训练2 图1-6-6所示是A、B两质点做直线运动的位移—时间图像,由图可知( )
A.A物体做匀速直线运动
B.B物体做曲线运动
C.t0内A、B两物体的位移相等
D.t0内A、B两物体的路程相等
图1-6-6
解析:选ACD.由图像知,A质点的位移随时间均匀增加,故A做匀速直线运动.B质点的位移不随时间均匀变化,所以B做变速直线运动.A、B两质点的位移都随着时间的增加而增大,A、B均做单方向直线运动,所以t0时间内,A、B的位移相等,路程相等.
v-t图像的理解及应用
某一做直线运动的物体的v-t图像如图1-6-7所示,根据图像求:
(1)物体距出发点的最远距离.
(2)前4 s物体的位移.
(3)前4 s内通过的路程.
例3
图1-6-7
【思路点拨】 解答本题应注意以下三点:
(1)v-t图像与t轴所围的“面积”表示物体位移大小.
(2)“面积”在t轴之上表示位移是正值,在下表示位移是负值.
(3)物体通过的路程为t轴上、下“面积”绝对值的和.
【答案】 (1)6 m (2)5 m (3)7 m
变式训练3 有一质点从t=0开始,由原点沿着x轴正方向出发,其速度—时间图像如图1-6-8所示,下列说法正确的是( )
A.t=1 s,质点离原点的距离最大
B.t=2 s,质点离原点的距离最大
C.t=2 s,质点回到原点
D.t=4 s,质点回到原点
图1-6-8
解析:选BD.前2 s内,物体一直向正方向运动,后2 s向反方向运动,故2 s末物体离原点最远,A错、B对;由图像的面积等于位移可知,前2 s物体向前运动了5 m,后2 s又返回了5 m,故4 s末物体又回到出发的原点,C错,D对.
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
