教科版高中物理必修1《运动快慢与方向的描述--速度》参考课件3(54张PPT)
文档属性
| 名称 | 教科版高中物理必修1《运动快慢与方向的描述--速度》参考课件3(54张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1011.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-05 00:00:00 | ||
图片预览











文档简介
(共54张PPT)
第三节
运动快慢与方向的描述——速度
课标定位:
应用:
1.利用公式计算物体运动的平均速度.
2.会用x-t图像和v-t图像描述匀速直线运动.
3.会用打点计时器测量物体运动的速度以及用v-t图像描述速度随时间的变化规律.
理解:
1.物体运动速度的意义以及速率与速度的区别.
2.平均速度的意义以及平均速度与瞬时速度的区别.
3.理解匀速运动的概念.
认识:
1.速度的定义式和矢量性,速率的概念.
2.测量物体运动速度大小的基本原理.
3.瞬时速度的意义.
第三节
核心要点突破
课堂互动讲练
课前自主学案
课标定位
课前自主学案
一、运动快慢的描述——速度
1.定义:位移与发生这段位移所用_____的比值.
2.定义式:v=_____= ,若物体沿直线运动,x1、x2分别为物体在t1、t2两时刻的位置,若x2>x1,说明物体的速度方向与x轴方向________,若x2<x1,则速度方向与x轴方向_______.
时间
相同
相反
3.物理意义:描述物体运动的______及运动方向.
4.单位:在国际单位制中是_______,符号是___________,另外在实用中还有_____、______等.
5.方向:速度是矢量,其方向就是物体_____的方向.
快慢
米每秒
m/s(m·s-1)
km/h
cm/s
运动
二、平均速度
1.定义:做变速直线运动的物体的位移Δx跟发生这段位移所用时间Δt的_______.
2.公式: _______.
比值
3.方向:物体在这一过程中发生的位移方向.
4.物理意义:表示做变速直线运动的物体在某一时间间隔内的平均快慢程度,只能粗略地描述物体的运动.
三、学生实验:用打点计时器测量平均速度
1.电火花打点计时器
(1)电火花打点计时器使用交流电源,工作电压是_______ V.
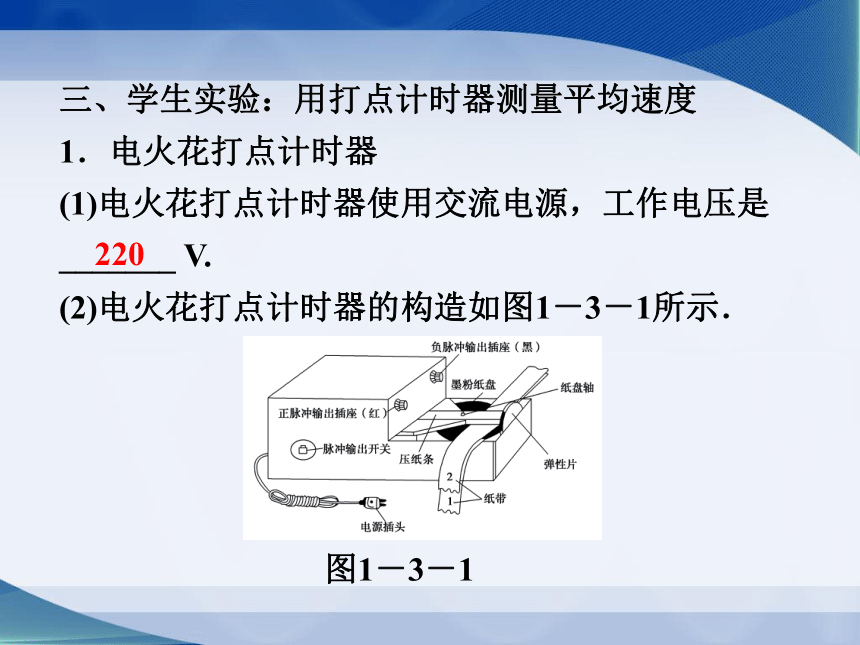
(2)电火花打点计时器的构造如图1-3-1所示.
220
图1-3-1
(3)工作原理:它是利用_________在纸带上打出孔而显示点迹的计时器.当接通220 V交流电源,按下脉冲输出开关时,计时器发出的脉冲电流经接正极的_______、墨粉纸盘到接负极的______,产生火花放电,于是在运动纸带上就打出一系列点迹.
当电源频率为50 Hz时,它每隔____ s打一次点,即打出的纸带上相邻两点间的时间间隔是____s.
火花放电
放电针
纸盘轴
0.02
0.02
2.实验步骤
(1)将木板固定在铁架台上,把打点计时器装在倾斜的木板上,将裁成圆片的墨粉纸套在纸盘轴上,将两条纸带(可用普通有光纸裁成)从弹性卡和纸盘之间的限位槽中穿过,并且将墨粉纸盘夹于两纸带之间.
(2)接通电源,然后将小车由_______释放,纸带上就打出一系列的点.
静止
(3)关闭电源,取下纸带,标注计数点(一般以0.1 s为时间间隔),如图1-3-2所示.
图1-3-2
3.分析与处理实验数据
(1)由纸带上的点迹判断小车运动的快慢(即速度是如何变化的).
(2)用刻度尺测量OA、OB、OC、OD、OE、OF间距离,求出对应的时间,用平均速度的公式得出对应的平均速度.
四、瞬时速度
1.定义:运动物体在某一______或某一位置的速度.
2.方向:运动物体在该时刻(或该位置)的运动方向.
3.物理意义:精确描述物体运动快慢.
4.速率:_______速度的大小.
时刻
瞬时
思考感悟
甲、乙两人从某地同时出发去超市购物,甲开车去,而乙骑电动车去,结果乙抄近路提前到达,试比较二人平均速度和瞬时速度的大小.
提示:若比较二人的平均速度大小,两人的位移相同,但乙用时间短些,故乙的平均速度大;若比较二人的瞬时速度,当然甲开车去的速度比乙大些.
五、速度—时间图像
1.速度—时间图像
以速度为纵轴,时间为横轴,建立一个平面直角坐标系,在该坐标系中画出物体的速度随时间的变化关系,这种描述速度v与时间t关系的图像叫做速度—时间图像(v-t图像),简称速度图像.
2.物理意义
v-t图像反映了运动物体的______随_______变化的规律,利用图像可判定物体的运动性质(是匀速运动还是变速运动).
速度
时间
3.对图像的认识
(1)匀速直线运动的图像是一条_______于时间轴的直线,它与时间轴围成的面积表示物体在这段时间内的,如图1-3-3所示.
平行
图1-3-3
(2)变速直线运动的图像可以是直线,也可以是曲线,如图1-3-4所示.
图1-3-4
核心要点突破
一、对平均速度和瞬时速度的理解
1.平均速度
(1)反映一段时间内物体运动的平均快慢程度,它与一段位移或一段时间相对应.
(2)在变速直线运动中,平均速度的大小跟选定的时间或位移有关,不同时间段内或不同位移上的平均速度一般不同,必须指明求出的平均速度是对应哪段时间内或哪段位移的平均速度,不指明对应过程的平均速度是没有意义的.
2.瞬时速度
(1)瞬时速度精确地描述了物体运动的快慢及方向,是矢量,一般情况下所提到的速度都是指瞬时速度.
(2)瞬时速度与某一时刻或某一位置相对应,即对应于某一状态.
(3)瞬时速度的方向就是该状态物体运动的方向.
3.两者的关系
(1)当位移足够小或时间足够短时,可以认为瞬时速度就等于平均速度.
(2)在匀速直线运动中,平均速度和瞬时速度相等.
特别提醒:(1)平均速度的大小与瞬时速度的大小没有必然的关系,即瞬时速度大的物体,其平均速度不一定大.
(2)平均速度与速度的平均值是不同的,速度的平均值并不一定等于平均速度.
即时应用?(即时突破,小试牛刀)
1.下列几个速度中表示平均速度的是( )
A.子弹出枪口的速度是800 m/s
B.汽车从甲站行驶到乙站的速度是40 km/h
C.汽车通过站牌时的速度是72 km/h
D.小球第3 s末的速度是6 m/s
解析:选B.平均速度对应的是一段时间或一段位移,而A、C、D三项对应的枪口、站牌、第3 s末都是位置或时刻,故A、C、D错,B对.
二、对瞬时速率和平均速率的理解
1.瞬时速率
瞬时速度的大小称为瞬时速率,一般称为速率.它是标量,只有大小,没有方向,它的大小反映了物体运动的快慢.
2.平均速率
(1)定义:运动物体通过的路程与通过这段路程所用时间的比值,是标量.
(2)说明:平均速率与平均速度的大小是两个完全不同的概念.由于在一般情况下质点的路程要大于位移的大小,所以平均速率一般也要大于平均速度的大小,只有在单向直线运动中,两者的大小才相等.
图1-3-5
3.二者联系:物体做速率不变的运动时(匀速率运动),瞬时速率等于平均速率,如匀速直线运动和匀速圆周运动.
特别提醒:
(1)瞬时速率为瞬时速度大小,但平均速率不是平均速度大小.
(2)某一运动过程中,瞬时速率可能大于平均速率,也可能小于或等于平均速率.
即时应用?(即时突破,小试牛刀)
2.关于瞬时速度、平均速度、平均速率,下列说法中正确的是( )
A.瞬时速度是物体在某一位置或某一时刻的速度
B.平均速度等于某段时间内物体运动的位移与所用时间的比值
C.做变速运动的物体,平均速率就是平均速度的大小
D.做变速运动的物体,平均速度是物体通过的路程与所用时间的比值
答案:AB
三、对v-t图像的理解
1.v-t图像的意义
v-t图像非常直观地反映了速度随时间变化的情况,但它并不是物体运动的轨迹.
2.匀速直线运动的v-t图像
从匀速直线运动的速度图像上可以得知物体速度的大小和方向. 直线在t轴 的上方速度为正,即与规定的正方向相同;在t轴下方速度为负,即与规定的正方向相反.如图1-3-6中的①、②所示.
图1-3-6
3.变速直线运动的v-t图像
(1)图像中的一个点代表物体在某一时刻的速度,图线远离时间轴代表速度增大,图线靠近时间轴代表速度减小.如图1-3-7中的a、b所示.
图1-3-7
(2)在v-t图像中,正、负号只表示方向不表示大小.不论速度是正还是负,只要速率增大,则表示物体做加速运动.如图1-3-8所示,图中0~2 s和3 s~4 s内物体都做加速运动,2 s~3 s和4 s~6 s 时间内,物体都做减速运动.
图1-3-8
(3)对于交点的理解
①两条图线相交,表明在该时刻两物体具有相同的速度,但不表示二者的位移相等.
②图线与t轴相交,表明此时刻物体的速度为零,图线跨过t轴表示运动方向改变.
③图线与v轴相交,表示物体的初速度.
特别提醒:不论v-t图像是直线还是曲线,都表示物体做直线运动,图像不是物体的运动轨迹.
即时应用?(即时突破,小试牛刀)
3.某物体运动的v-t图像如图1-3-9所示,则该物体( )
A.做往复运动
B.做匀速直线运动
C.朝某一方向做直线运动
D.以上说法均不正确
图1-3-9
解析:选C.由于v的大小随时间变化是先增大后减小,再增大再减小,所以不是匀速直线运动.加速度的方向在变化,也不是匀变速运动,但由于v的方向始终没变,所以物体朝一个方向运动.
课堂互动讲练
对平均速度和瞬时速度的理解
下面关于瞬时速度和平均速度的说法正确的是( )
A.若物体在某段时间内每时刻的瞬时速度都等于零,则它在这段时间内的平均速度一定等于零
B.若物体在某段时间内的平均速度等于零,则它在这段时间内任一时刻的瞬时速度一定等于零
例1
C.匀速直线运动中任意一段时间内的平均速度都等于它任一时刻的瞬时速度
D.变速直线运动中任意一段时间内的平均速度一定不等于它某一时刻的瞬时速度
【思路点拨】 要明确平均速度和瞬时速度的概念,平均速度描述一个过程中的运动,但不能精确地描述物体在某个时刻或位置的运动,瞬时速度是用来精确描述物体在某个时刻或位置的运动,平均速度与瞬时速度在数量上没有确定的关系.
【精讲精析】 每个时刻瞬时速度都等于零,平均速度一定等于零.但是某段时间内平均速度等于零,任一时刻的瞬时速度不一定等于零,例如质点的往复运动,A项对,B项错.
匀速直线运动中,由于相等时间内位移相等,而且位移的大小和路程相等,所以C项对.
变速运动一段时间内的平均速度有可能等于某时刻瞬时速度,所以D项错.
【答案】 AC
变式训练1 下列说法中正确的是( )
A.做匀速直线运动的物体,任一时刻的瞬时速度都相等
B.做匀速直线运动的物体,任一段时间内的平均速度都相等
C.在任意相等的时间内平均速度都相等的运动是匀速直线运动
D.如果物体运动的路程跟所需时间的比值是一个恒量,则这种运动是匀速直线运动
解析:选ABC.物体做匀速直线运动,物体在任意时刻通过任意一个位置,任意一段时间内,通过任意一段位移,它们的速度都相等,故A、B选项正确;在任意相等的时间内平均速度都相等,也就意味着相等时间内通过的位移相等,物体做匀速直线运动,故C对;物体运动的路程跟所用时间的比值为一个恒量,只能说明是匀速率运动,但不能说为匀速直线运动,显然D不对.
平均速度的计算
某质点由A出发做直线运动,前5 s向东行了30 m经过B点,又行了5 s前进了60 m到达C点,在C点停了4 s后又向西行,经历了6 s运动120 m到达A点西侧的D点.如图1-3-10所示,求:
(1)全过程的平均速度;
(2)全过程的平均速率.
例2
图1-3-10
【思路点拨】
解答本题时应注意以下三个方面:
(1)平均速度与平均速率的区别.
(2)全过程的位移与路程的计算.
(3)时间的确定.
【答案】
(1)1.5 m/s ,方向向西 (2)10.5 m/s
【方法总结】
(1)一般的变速直线运动,求平均速度时,要紧扣定义找位移及该位移对应的时间,不要仅凭想当然来编造公式.
(2)平均速度与时间有关,不同时间内的平均速度不一定相同,所以,对平均速度要明确是哪段时间内的平均速度.
变式训练2 一辆汽车沿笔直的公路行驶,第1 s内通过5 m的距离,第2 s内和第3 s内各通过20 m的距离,第4 s内又通过15 m的距离,求汽车在最初2 s内的平均速度和这4 s内的平均速度各是多少?
解析:前2 s时间为2 s,位移为(5+20) m,前4 s时间为4 s,位移为(5+20+20+15) m.根据平均速度的定义式得
答案:12.5 m/s 15 m/s
利用纸带计算平均速度和瞬时速度
打点计时器所用电源的频率为50 Hz,某次实验中得到一条纸带,用毫米刻度尺测量的情况如图1-3-11所示,纸带上A、C两点对应的时间为_____ s,纸带在A、C间的平均速度为_____m/s.在A、D间的平均速度为_______ m/s.二者之间B点的瞬时速度更接近于_______ m/s.
例3
B点的瞬时速度更接近于A、C间的平均速度,
即vB≈0.35 m/s.
【答案】 0.04 0.35 0.43 0.35
【方法总结】
(1)利用mm刻度尺测间距时要估读到0.1 mm位.
(2)分清打点时间间隔与计数点间时间间隔.
(3)以计数点为中心的两点间的平均速度最接近该点的瞬时速度.
变式训练3 如图1-3-12所示为某次实验时打出的纸带,打点计时器每隔0.02 s打一个点,图中O点为第一个点,A、B、C、D为每隔一点选定的计数点.根据图中标出的数据,打A、D点时间内纸带的平均速度是________,打B点时刻纸带的瞬时速度是________.
图1-3-12
答案:231.25 cm/s 212.50 cm/s
对v-t图像的理解及应用
图1-3-13是甲、乙两物体运动的速度图像,下列说法正确的是( )
A.物体甲处于静止状态
B.物体乙刚开始时以5 m/s的速度与
甲物体同向运动
C.物体乙在最初3 s内的位移是10 m
D.物体乙在最初3 s内的路程是10 m
例4
图1-3-13
【自主解答】 甲速度图像是平行于t轴的直线,因此甲做匀速直线运动,A错误.乙物体在第1 s内向正方向做速度为5 m/s的匀速直线运动,第2 s内静止,第3 s内沿负方向做速率为5 m/s的匀速直线运动.故B正确;乙在第1 s内的位移为x1=v1t1=5 m,在第2 s内的位移为x2=0,在第3 s内的位移为x3=v3t3=-5 m,所以物体乙在最初3 s内的位移为x=x1+x2+x3=0,故C错;物体乙在最初3 s内的路程为:s=|x1|+|x2|+|x3|=10 m,故D对.
【答案】 BD
变式训练4 某物体沿一直线运动,其v-t图像如图1-3-14所示,则下列说法中正确的是( )
A.第2 s内和第3 s内速度方向相反
B.第2 s内和第3 s内速度方向相同
C.第2 s末速度方向发生变化
D.第5 s内与第1 s内速度方向相同
图1-3-14
解析:选B.v-t图像中在时间轴上面的部分方向为正,在时间轴下面的方向为负,故A、D错B对;在第2 s末速度最大,方向没变,故C错.
第三节
运动快慢与方向的描述——速度
课标定位:
应用:
1.利用公式计算物体运动的平均速度.
2.会用x-t图像和v-t图像描述匀速直线运动.
3.会用打点计时器测量物体运动的速度以及用v-t图像描述速度随时间的变化规律.
理解:
1.物体运动速度的意义以及速率与速度的区别.
2.平均速度的意义以及平均速度与瞬时速度的区别.
3.理解匀速运动的概念.
认识:
1.速度的定义式和矢量性,速率的概念.
2.测量物体运动速度大小的基本原理.
3.瞬时速度的意义.
第三节
核心要点突破
课堂互动讲练
课前自主学案
课标定位
课前自主学案
一、运动快慢的描述——速度
1.定义:位移与发生这段位移所用_____的比值.
2.定义式:v=_____= ,若物体沿直线运动,x1、x2分别为物体在t1、t2两时刻的位置,若x2>x1,说明物体的速度方向与x轴方向________,若x2<x1,则速度方向与x轴方向_______.
时间
相同
相反
3.物理意义:描述物体运动的______及运动方向.
4.单位:在国际单位制中是_______,符号是___________,另外在实用中还有_____、______等.
5.方向:速度是矢量,其方向就是物体_____的方向.
快慢
米每秒
m/s(m·s-1)
km/h
cm/s
运动
二、平均速度
1.定义:做变速直线运动的物体的位移Δx跟发生这段位移所用时间Δt的_______.
2.公式: _______.
比值
3.方向:物体在这一过程中发生的位移方向.
4.物理意义:表示做变速直线运动的物体在某一时间间隔内的平均快慢程度,只能粗略地描述物体的运动.
三、学生实验:用打点计时器测量平均速度
1.电火花打点计时器
(1)电火花打点计时器使用交流电源,工作电压是_______ V.
(2)电火花打点计时器的构造如图1-3-1所示.
220
图1-3-1
(3)工作原理:它是利用_________在纸带上打出孔而显示点迹的计时器.当接通220 V交流电源,按下脉冲输出开关时,计时器发出的脉冲电流经接正极的_______、墨粉纸盘到接负极的______,产生火花放电,于是在运动纸带上就打出一系列点迹.
当电源频率为50 Hz时,它每隔____ s打一次点,即打出的纸带上相邻两点间的时间间隔是____s.
火花放电
放电针
纸盘轴
0.02
0.02
2.实验步骤
(1)将木板固定在铁架台上,把打点计时器装在倾斜的木板上,将裁成圆片的墨粉纸套在纸盘轴上,将两条纸带(可用普通有光纸裁成)从弹性卡和纸盘之间的限位槽中穿过,并且将墨粉纸盘夹于两纸带之间.
(2)接通电源,然后将小车由_______释放,纸带上就打出一系列的点.
静止
(3)关闭电源,取下纸带,标注计数点(一般以0.1 s为时间间隔),如图1-3-2所示.
图1-3-2
3.分析与处理实验数据
(1)由纸带上的点迹判断小车运动的快慢(即速度是如何变化的).
(2)用刻度尺测量OA、OB、OC、OD、OE、OF间距离,求出对应的时间,用平均速度的公式得出对应的平均速度.
四、瞬时速度
1.定义:运动物体在某一______或某一位置的速度.
2.方向:运动物体在该时刻(或该位置)的运动方向.
3.物理意义:精确描述物体运动快慢.
4.速率:_______速度的大小.
时刻
瞬时
思考感悟
甲、乙两人从某地同时出发去超市购物,甲开车去,而乙骑电动车去,结果乙抄近路提前到达,试比较二人平均速度和瞬时速度的大小.
提示:若比较二人的平均速度大小,两人的位移相同,但乙用时间短些,故乙的平均速度大;若比较二人的瞬时速度,当然甲开车去的速度比乙大些.
五、速度—时间图像
1.速度—时间图像
以速度为纵轴,时间为横轴,建立一个平面直角坐标系,在该坐标系中画出物体的速度随时间的变化关系,这种描述速度v与时间t关系的图像叫做速度—时间图像(v-t图像),简称速度图像.
2.物理意义
v-t图像反映了运动物体的______随_______变化的规律,利用图像可判定物体的运动性质(是匀速运动还是变速运动).
速度
时间
3.对图像的认识
(1)匀速直线运动的图像是一条_______于时间轴的直线,它与时间轴围成的面积表示物体在这段时间内的,如图1-3-3所示.
平行
图1-3-3
(2)变速直线运动的图像可以是直线,也可以是曲线,如图1-3-4所示.
图1-3-4
核心要点突破
一、对平均速度和瞬时速度的理解
1.平均速度
(1)反映一段时间内物体运动的平均快慢程度,它与一段位移或一段时间相对应.
(2)在变速直线运动中,平均速度的大小跟选定的时间或位移有关,不同时间段内或不同位移上的平均速度一般不同,必须指明求出的平均速度是对应哪段时间内或哪段位移的平均速度,不指明对应过程的平均速度是没有意义的.
2.瞬时速度
(1)瞬时速度精确地描述了物体运动的快慢及方向,是矢量,一般情况下所提到的速度都是指瞬时速度.
(2)瞬时速度与某一时刻或某一位置相对应,即对应于某一状态.
(3)瞬时速度的方向就是该状态物体运动的方向.
3.两者的关系
(1)当位移足够小或时间足够短时,可以认为瞬时速度就等于平均速度.
(2)在匀速直线运动中,平均速度和瞬时速度相等.
特别提醒:(1)平均速度的大小与瞬时速度的大小没有必然的关系,即瞬时速度大的物体,其平均速度不一定大.
(2)平均速度与速度的平均值是不同的,速度的平均值并不一定等于平均速度.
即时应用?(即时突破,小试牛刀)
1.下列几个速度中表示平均速度的是( )
A.子弹出枪口的速度是800 m/s
B.汽车从甲站行驶到乙站的速度是40 km/h
C.汽车通过站牌时的速度是72 km/h
D.小球第3 s末的速度是6 m/s
解析:选B.平均速度对应的是一段时间或一段位移,而A、C、D三项对应的枪口、站牌、第3 s末都是位置或时刻,故A、C、D错,B对.
二、对瞬时速率和平均速率的理解
1.瞬时速率
瞬时速度的大小称为瞬时速率,一般称为速率.它是标量,只有大小,没有方向,它的大小反映了物体运动的快慢.
2.平均速率
(1)定义:运动物体通过的路程与通过这段路程所用时间的比值,是标量.
(2)说明:平均速率与平均速度的大小是两个完全不同的概念.由于在一般情况下质点的路程要大于位移的大小,所以平均速率一般也要大于平均速度的大小,只有在单向直线运动中,两者的大小才相等.
图1-3-5
3.二者联系:物体做速率不变的运动时(匀速率运动),瞬时速率等于平均速率,如匀速直线运动和匀速圆周运动.
特别提醒:
(1)瞬时速率为瞬时速度大小,但平均速率不是平均速度大小.
(2)某一运动过程中,瞬时速率可能大于平均速率,也可能小于或等于平均速率.
即时应用?(即时突破,小试牛刀)
2.关于瞬时速度、平均速度、平均速率,下列说法中正确的是( )
A.瞬时速度是物体在某一位置或某一时刻的速度
B.平均速度等于某段时间内物体运动的位移与所用时间的比值
C.做变速运动的物体,平均速率就是平均速度的大小
D.做变速运动的物体,平均速度是物体通过的路程与所用时间的比值
答案:AB
三、对v-t图像的理解
1.v-t图像的意义
v-t图像非常直观地反映了速度随时间变化的情况,但它并不是物体运动的轨迹.
2.匀速直线运动的v-t图像
从匀速直线运动的速度图像上可以得知物体速度的大小和方向. 直线在t轴 的上方速度为正,即与规定的正方向相同;在t轴下方速度为负,即与规定的正方向相反.如图1-3-6中的①、②所示.
图1-3-6
3.变速直线运动的v-t图像
(1)图像中的一个点代表物体在某一时刻的速度,图线远离时间轴代表速度增大,图线靠近时间轴代表速度减小.如图1-3-7中的a、b所示.
图1-3-7
(2)在v-t图像中,正、负号只表示方向不表示大小.不论速度是正还是负,只要速率增大,则表示物体做加速运动.如图1-3-8所示,图中0~2 s和3 s~4 s内物体都做加速运动,2 s~3 s和4 s~6 s 时间内,物体都做减速运动.
图1-3-8
(3)对于交点的理解
①两条图线相交,表明在该时刻两物体具有相同的速度,但不表示二者的位移相等.
②图线与t轴相交,表明此时刻物体的速度为零,图线跨过t轴表示运动方向改变.
③图线与v轴相交,表示物体的初速度.
特别提醒:不论v-t图像是直线还是曲线,都表示物体做直线运动,图像不是物体的运动轨迹.
即时应用?(即时突破,小试牛刀)
3.某物体运动的v-t图像如图1-3-9所示,则该物体( )
A.做往复运动
B.做匀速直线运动
C.朝某一方向做直线运动
D.以上说法均不正确
图1-3-9
解析:选C.由于v的大小随时间变化是先增大后减小,再增大再减小,所以不是匀速直线运动.加速度的方向在变化,也不是匀变速运动,但由于v的方向始终没变,所以物体朝一个方向运动.
课堂互动讲练
对平均速度和瞬时速度的理解
下面关于瞬时速度和平均速度的说法正确的是( )
A.若物体在某段时间内每时刻的瞬时速度都等于零,则它在这段时间内的平均速度一定等于零
B.若物体在某段时间内的平均速度等于零,则它在这段时间内任一时刻的瞬时速度一定等于零
例1
C.匀速直线运动中任意一段时间内的平均速度都等于它任一时刻的瞬时速度
D.变速直线运动中任意一段时间内的平均速度一定不等于它某一时刻的瞬时速度
【思路点拨】 要明确平均速度和瞬时速度的概念,平均速度描述一个过程中的运动,但不能精确地描述物体在某个时刻或位置的运动,瞬时速度是用来精确描述物体在某个时刻或位置的运动,平均速度与瞬时速度在数量上没有确定的关系.
【精讲精析】 每个时刻瞬时速度都等于零,平均速度一定等于零.但是某段时间内平均速度等于零,任一时刻的瞬时速度不一定等于零,例如质点的往复运动,A项对,B项错.
匀速直线运动中,由于相等时间内位移相等,而且位移的大小和路程相等,所以C项对.
变速运动一段时间内的平均速度有可能等于某时刻瞬时速度,所以D项错.
【答案】 AC
变式训练1 下列说法中正确的是( )
A.做匀速直线运动的物体,任一时刻的瞬时速度都相等
B.做匀速直线运动的物体,任一段时间内的平均速度都相等
C.在任意相等的时间内平均速度都相等的运动是匀速直线运动
D.如果物体运动的路程跟所需时间的比值是一个恒量,则这种运动是匀速直线运动
解析:选ABC.物体做匀速直线运动,物体在任意时刻通过任意一个位置,任意一段时间内,通过任意一段位移,它们的速度都相等,故A、B选项正确;在任意相等的时间内平均速度都相等,也就意味着相等时间内通过的位移相等,物体做匀速直线运动,故C对;物体运动的路程跟所用时间的比值为一个恒量,只能说明是匀速率运动,但不能说为匀速直线运动,显然D不对.
平均速度的计算
某质点由A出发做直线运动,前5 s向东行了30 m经过B点,又行了5 s前进了60 m到达C点,在C点停了4 s后又向西行,经历了6 s运动120 m到达A点西侧的D点.如图1-3-10所示,求:
(1)全过程的平均速度;
(2)全过程的平均速率.
例2
图1-3-10
【思路点拨】
解答本题时应注意以下三个方面:
(1)平均速度与平均速率的区别.
(2)全过程的位移与路程的计算.
(3)时间的确定.
【答案】
(1)1.5 m/s ,方向向西 (2)10.5 m/s
【方法总结】
(1)一般的变速直线运动,求平均速度时,要紧扣定义找位移及该位移对应的时间,不要仅凭想当然来编造公式.
(2)平均速度与时间有关,不同时间内的平均速度不一定相同,所以,对平均速度要明确是哪段时间内的平均速度.
变式训练2 一辆汽车沿笔直的公路行驶,第1 s内通过5 m的距离,第2 s内和第3 s内各通过20 m的距离,第4 s内又通过15 m的距离,求汽车在最初2 s内的平均速度和这4 s内的平均速度各是多少?
解析:前2 s时间为2 s,位移为(5+20) m,前4 s时间为4 s,位移为(5+20+20+15) m.根据平均速度的定义式得
答案:12.5 m/s 15 m/s
利用纸带计算平均速度和瞬时速度
打点计时器所用电源的频率为50 Hz,某次实验中得到一条纸带,用毫米刻度尺测量的情况如图1-3-11所示,纸带上A、C两点对应的时间为_____ s,纸带在A、C间的平均速度为_____m/s.在A、D间的平均速度为_______ m/s.二者之间B点的瞬时速度更接近于_______ m/s.
例3
B点的瞬时速度更接近于A、C间的平均速度,
即vB≈0.35 m/s.
【答案】 0.04 0.35 0.43 0.35
【方法总结】
(1)利用mm刻度尺测间距时要估读到0.1 mm位.
(2)分清打点时间间隔与计数点间时间间隔.
(3)以计数点为中心的两点间的平均速度最接近该点的瞬时速度.
变式训练3 如图1-3-12所示为某次实验时打出的纸带,打点计时器每隔0.02 s打一个点,图中O点为第一个点,A、B、C、D为每隔一点选定的计数点.根据图中标出的数据,打A、D点时间内纸带的平均速度是________,打B点时刻纸带的瞬时速度是________.
图1-3-12
答案:231.25 cm/s 212.50 cm/s
对v-t图像的理解及应用
图1-3-13是甲、乙两物体运动的速度图像,下列说法正确的是( )
A.物体甲处于静止状态
B.物体乙刚开始时以5 m/s的速度与
甲物体同向运动
C.物体乙在最初3 s内的位移是10 m
D.物体乙在最初3 s内的路程是10 m
例4
图1-3-13
【自主解答】 甲速度图像是平行于t轴的直线,因此甲做匀速直线运动,A错误.乙物体在第1 s内向正方向做速度为5 m/s的匀速直线运动,第2 s内静止,第3 s内沿负方向做速率为5 m/s的匀速直线运动.故B正确;乙在第1 s内的位移为x1=v1t1=5 m,在第2 s内的位移为x2=0,在第3 s内的位移为x3=v3t3=-5 m,所以物体乙在最初3 s内的位移为x=x1+x2+x3=0,故C错;物体乙在最初3 s内的路程为:s=|x1|+|x2|+|x3|=10 m,故D对.
【答案】 BD
变式训练4 某物体沿一直线运动,其v-t图像如图1-3-14所示,则下列说法中正确的是( )
A.第2 s内和第3 s内速度方向相反
B.第2 s内和第3 s内速度方向相同
C.第2 s末速度方向发生变化
D.第5 s内与第1 s内速度方向相同
图1-3-14
解析:选B.v-t图像中在时间轴上面的部分方向为正,在时间轴下面的方向为负,故A、D错B对;在第2 s末速度最大,方向没变,故C错.
同课章节目录
- 第一章 运动的描述
- 1 质点 参考系 空间 时间
- 2 位置变化的描述——位移
- 3 运动快慢与方向的描述——速度
- 4 速度变化快慢的描述——加速度
- 5 匀变速直线运动速度与时间的关系
- 6 匀变速直线运动位移与时间的关系
- 7 对自由落体运动的研究
- 8 匀变速直线运动规律的应用
- 9 测定匀变速直线运动的加速度
- 第二章 力
- 1 力
- 2 重力
- 3 弹力
- 4 摩擦力
- 5 力的合成
- 6 力的分解
- 第三章 牛顿运动定律
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿第三定律
- 5 牛顿运动定律的应用
- 6 超重与失重
- 第四章 物体的平衡
- 1 共点力作用下物体的平衡
- 2 共点力平衡条件的应用
- 3 平衡的稳定性(选学)
