教科版高中物理选修3-5《动量守恒研究》复习课件2(27张PPT)
文档属性
| 名称 | 教科版高中物理选修3-5《动量守恒研究》复习课件2(27张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1013.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-05 15:46:53 | ||
图片预览







文档简介
(共27张PPT)
动量守恒定律
复 习
一、动量守恒定律的内容
相互作用的几个物体组成的系统,如果不受外力作用,或它们受到的外力之和为0,则系统的总动量保持不变.
二、动量守恒定律的适用条件
内力不改变系统的总动量,外力才能改变系统的总动量,在下列三种情况下,可以使用动量守恒定律:
(1)系统不受外力或所受外力的矢量和为0.
(2)系统所受外力远小于内力,如碰撞或爆炸瞬间,外力可以忽略不计.
(3)系统某一方向不受外力或所受外力的矢量和为0,或外力远小于内力,则该方向动量守恒(分动量守恒).
三、动量守恒定律的不同表达形式及含义
1.p=p′(系统相互作用前总动量p等于相互作用后总动量p′)
对于两个物体组成的系统
2.ΔΡ=0(系统总动量的增量等于0);
3. ΔΡ1=- ΔΡ2(两个物体组成的系统中,各自动量增量大小相等、方向相反),
其中①的形式最常用,常见的三种情形
注意:
1.m1v1+m2v2=m1v′1+m2v′2
(适用于作用前后都运动的两个物体组成的系统).
2. m1v1+ m2v2 =0
(适用于原来静止的两个物体组成的系统,比如爆炸、反冲等,两者速率及位移大小与各自质量成反比).
3. m1v1+ m2v2 =(m1+m2)v
(适用于两物体作用后结合在一起或具有共同速度的情况).
四、理解要点
1.动量守恒定律的研究对象是相互作用物体组成的系统.
2.系统“总动量不变”不仅是系统初、末两个时刻总动量相等,而且是指系统在整个过程中任意两个时刻的总动量都相等.
3.式子是矢量式,根据教学大纲,动量守恒定律应用只限于一维情况.应用时,先选定正方向,而后将矢量式化为代数式.
五、应用动量守恒定律解题的基本步骤
(1)分析题意,明确研究对象,在分析相互作用的物体的总动量是否守恒时,通常把这些被研究的物体总称为系统.要明确所研究的系统是由哪几个物体组成的.
(2)要对系统内的物体进行受力分析,弄清哪些是系统内部物体之间相互作用的力,即内力;哪些是系统外的物体对系统内物体的作用力,即外力.
在受力分析的基础上,根据动量守恒的条件,判断能否应用动量守恒定律.
(3)明确所研究的相互作用过程,确定过程的始、末状态,即系统内各个物体的初动量和末动量的量值或表达式.
注意在选取某个已知量的方向为正方向以后,凡是和选定的正方向同向的已知量取正值,反向的取负值.
(4)建立动量守恒方程,代入已知量,解出待求量,计算结果如果是正的,说明该量的方向和正方向相同,如果是负的,则和选定的正方向相反.
六、典型模型(问题):
5、多物体、多过程问题
4、碰撞问题
1、人船模型
3、小球弹簧问题
2、子弹打木块模型
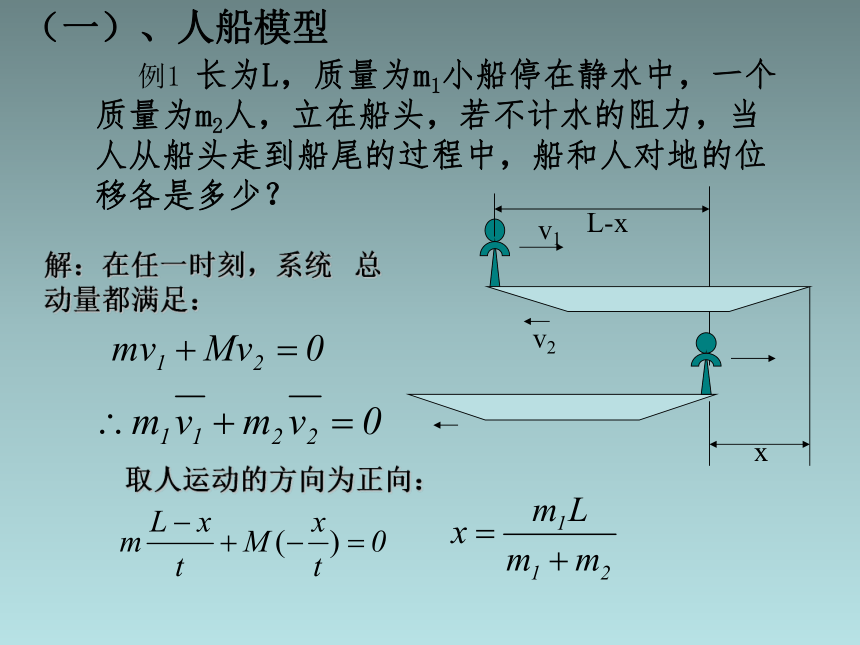
x
v1
L-x
v2
例1 长为L,质量为m1小船停在静水中,一个质量为m2人,立在船头,若不计水的阻力,当人从船头走到船尾的过程中,船和人对地的位移各是多少?
解:在任一时刻,系统 总 动量都满足:
取人运动的方向为正向:
(一)、人船模型
`
`
`
`
`
`
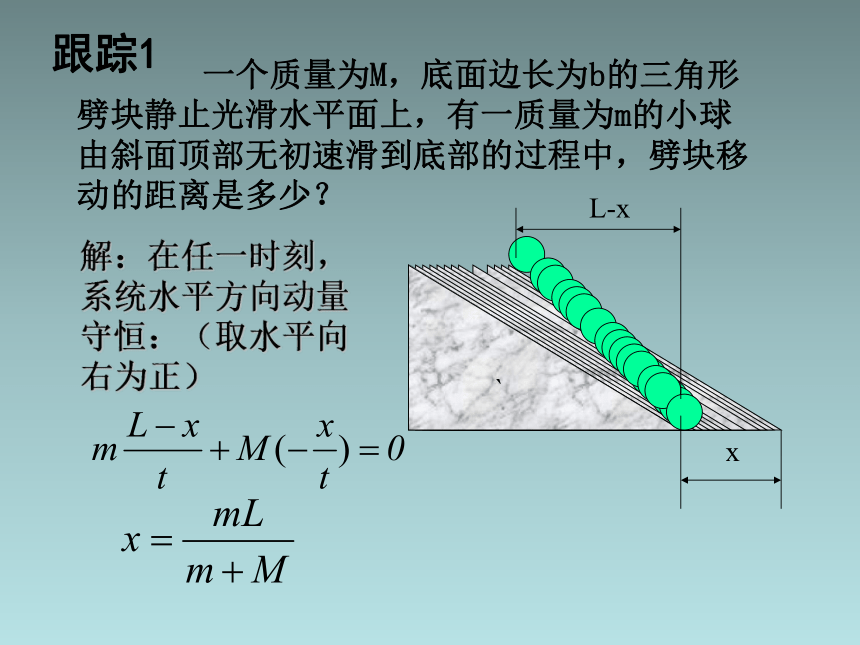
x
L-x
一个质量为M,底面边长为b的三角形劈块静止光滑水平面上,有一质量为m的小球由斜面顶部无初速滑到底部的过程中,劈块移动的距离是多少?
解:在任一时刻,系统水平方向动量守恒:(取水平向右为正)
跟踪1
变式训练:如图所示,总质量为M的气球下端悬着质量为m的人而静止于高度为h的空中,欲使人能沿着绳安全着地,人下方的绳至少应为多长?
例2:设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,设木块对子弹的阻力恒为f,求:
1.木块至少多长子弹才不会穿出
2.子弹在木块中运动了多长时间
(二)、子弹打木块问题
(1)解:从动量的角度看,以m和M组成的系统为研究对象,根据动量守恒
对子弹用动能定理:
对木块用动能定理:
①、②相减得:
由上式可得:
……①
……②
……③
(2)以子弹为研究对象,由牛顿运动定律和运动学公式可得:
从能量的角度看,该过程系统损失的动能全部转化为系统的内能。设平均阻力大小为f,设子弹、木块的位移大小分别为s1、s2,如图所示,显然有s1-s2=L
总结:
子弹打木块的模型具有下列力学规律:
1、动力学的规律:构成系统的两物体在相互作用时,受到大小相等,方向相反的一对恒力的作用,他们的加速度大小与质量成反比,方向相反。
2、运动学的规律:在子弹进入木块的过程中,可以看成是匀减速运动,木块做匀加速运动,子弹的进入深度就是他们的相对位移。
3、动量和能量规律:系统的动量守恒,系统内各物体的动能发生变化,作用力对子弹做的功等于子弹动能的变化,作用力对木块做的功等于木块动能的变化,系统动能转化为内能,其大小等于该恒力的大小与相对位移的乘积。
A.动量守恒,机械能守恒
B.动量不守恒,机械能不守恒
C.弹性势能由最大变到最小
D.机械能由最大值变为稳定值
跟踪2 如图所示的装置中,木块B与水平桌面间的接触是光滑的,子弹A沿水平方向射入木块后留在木块内,弹簧被压缩,现将子弹、木块和弹簧合在一起作为研究系统,则此系统在从子弹开始射入到弹簧被压缩到最短的整个过程中 [ ]
(三)、小球弹簧问题
例3:如图甲所示,一轻质弹簧的两端与质量分别为m1和m2的两物块A、B相连接,并静止在光滑的水平面上.现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得( )
A.在t1、t3时刻两物块达到共同速度1m/s,且弹簧都是处于压缩状态
B.从t3到t4时刻弹簧由压缩状态恢复到原长
C.两物体的质量之比为m1:m2=1:2
D.在t2时刻A和B的动能之比为Ek1: Ek2=1:8
跟踪3:质量为m的物块甲以3m/s的速度在光滑水平面上运动,有一轻弹簧固定其上,另一质量也为m的物体乙以4m/s的速度与甲相向运动,如图所示。则( )
A.甲、乙两物块在弹簧压缩过程中,由于弹力作用,动量不守恒
B.当两物块相距最近时,甲物块的速率为零
C.当甲物块的速率为1m/s时,乙物块的速率可能为2m/s,也可能为0
D.甲物块的速率可能达到5m/s
3、碰撞三原则:
1、碰撞过程的特点:
直接作用、时间短、内力远大于外力
C、完全非弹性碰撞
2、碰撞的规律:
a、弹性碰撞
b、非弹性碰撞
a、动量守恒 b、动能不增加
C、碰撞前后要符合实际,即不可能发生第二次碰撞
(四)、碰撞问题
例4
一辆质量为M的小车以速率v1在光滑的水平面上运动时,恰遇一质量为m,速率为v2物体以俯角60。的速度方向落在车上并陷于车里的砂中,求此后车的速度。
60。
v2
v1
v’
解:系统水平方向不受外力,水平方向动量守恒:(取v2方向为正向)
例5
一个中子以2.0×107m/s的速度撞到一个静止的原子核上,已知中子以1.7 × 107m/s的速度被反弹回来,那个原子核以3.1 × 107m/s的速度向前运动,求原子核的质量数。
v
m
M
v‘
V
系统动量守恒,取v的方向为正方向:
原子核的质量数为12。
例6、质量相等的A、B两球在光滑水平面上沿一直线向同一方向运动,A球的动量为PA=7kg·m/s,B球的动量为PB =5kg·m/s,当A球追上B球发生碰撞,则碰撞后A、B两球的动量可能为( )
A.
B.
C.
D.
变式训练: 如图所示,光滑水平面上质量为m1=2kg的物块以v0=2m/s的初速冲向质量为m2=6kg静止的光滑1/4圆弧面斜劈体。求:
m1
m2
v0
5、分析与比较:下面的模型与该题的异同?
v0
1、物块m1滑到最高点位置时,二者的速度
2、 m1上升的最大高度
3、物块m1从圆弧面滑下后,二者速度
4、若m1= m2物块m1从圆弧面滑下后,二者速度
总结:解碰撞类的动量守恒注意
1、规律的应用:
动量守恒和能量守恒的综合应用。
2、注意三个制约因素:
动量守恒,能量不增加,运动要合理。
3、会情境迁移:
能把题目中的新的情境转化为自己熟悉的类型。
如图所示,A、B两木块的质量之比为3:2,原来静止在平板小车C上,A、B间有一根被压缩了的轻弹簧,A、B与平板车的上表面间的动摩擦因素相同,地面光滑。当弹簧突然释放后,A、B在小车上滑动时有:
1)A、B系统动量守恒
2)A、B、C系统动量守恒
3) 小车向左运动
4) 小车向右运动
例7
A
B
C
5、多物体、多过程问题
人和小车的总质量为M,人坐在静止于光滑水平面的小车上,以相对地的速率v 将一质量为m 的木箱沿水平面推向正前方的竖直固定挡板。设箱与挡板碰撞时无机械能损失,碰撞后箱以速率v反弹回来。人接住箱后,再以同样的相对于地的速率v 将木箱沿水平面推向正前方的挡板。已知M:m=4:1,求:
(1)人第二次推出箱后,小车和人的速度大小。
(2)人推箱多少次后不能再接到箱?
练习
解:每次推箱时,对小车、人和木箱组成的系统,动量守恒,设人和小车速度方向为正方向,每次推箱后人和小车的速度分别为v1、v2…,
则第一次推箱后:Mv1-mv=0 ⑴
第一次推箱前
第一次推箱后
解:每次推箱时,对小车、人和木箱组成的系统,动量守恒,设人和小车速度方向为正方向,每次推箱后人和小车的速度分别为v1、v2…,
第二次推箱前
第二次推箱后
第二次推箱后: Mv2-mv = (M +m )V1′ ⑶
解:每次推箱时,对小车、人和木箱组成的系统,动量守恒,设人和小车速度方向为正方向,每次推箱后人和小车的速度分别为v1、v2…,
则第一次推箱后:Mv1-mv=0 ⑴
第一次接箱后:(M +m )V1′= Mv1 + mv ⑵
第二次推箱后: Mv2-mv = (M +m )V1′ ⑶
∴v2=3mv/M
以此类推,第N次推箱后,人和小车的速度
vN=(2N-1)mv/M
当vN>v时,不再能接到箱,即
2N-1>M/m=4 N>2.5.25
∴人推箱3次后不能再接到箱
∴v1=mv/M
动量守恒定律
复 习
一、动量守恒定律的内容
相互作用的几个物体组成的系统,如果不受外力作用,或它们受到的外力之和为0,则系统的总动量保持不变.
二、动量守恒定律的适用条件
内力不改变系统的总动量,外力才能改变系统的总动量,在下列三种情况下,可以使用动量守恒定律:
(1)系统不受外力或所受外力的矢量和为0.
(2)系统所受外力远小于内力,如碰撞或爆炸瞬间,外力可以忽略不计.
(3)系统某一方向不受外力或所受外力的矢量和为0,或外力远小于内力,则该方向动量守恒(分动量守恒).
三、动量守恒定律的不同表达形式及含义
1.p=p′(系统相互作用前总动量p等于相互作用后总动量p′)
对于两个物体组成的系统
2.ΔΡ=0(系统总动量的增量等于0);
3. ΔΡ1=- ΔΡ2(两个物体组成的系统中,各自动量增量大小相等、方向相反),
其中①的形式最常用,常见的三种情形
注意:
1.m1v1+m2v2=m1v′1+m2v′2
(适用于作用前后都运动的两个物体组成的系统).
2. m1v1+ m2v2 =0
(适用于原来静止的两个物体组成的系统,比如爆炸、反冲等,两者速率及位移大小与各自质量成反比).
3. m1v1+ m2v2 =(m1+m2)v
(适用于两物体作用后结合在一起或具有共同速度的情况).
四、理解要点
1.动量守恒定律的研究对象是相互作用物体组成的系统.
2.系统“总动量不变”不仅是系统初、末两个时刻总动量相等,而且是指系统在整个过程中任意两个时刻的总动量都相等.
3.式子是矢量式,根据教学大纲,动量守恒定律应用只限于一维情况.应用时,先选定正方向,而后将矢量式化为代数式.
五、应用动量守恒定律解题的基本步骤
(1)分析题意,明确研究对象,在分析相互作用的物体的总动量是否守恒时,通常把这些被研究的物体总称为系统.要明确所研究的系统是由哪几个物体组成的.
(2)要对系统内的物体进行受力分析,弄清哪些是系统内部物体之间相互作用的力,即内力;哪些是系统外的物体对系统内物体的作用力,即外力.
在受力分析的基础上,根据动量守恒的条件,判断能否应用动量守恒定律.
(3)明确所研究的相互作用过程,确定过程的始、末状态,即系统内各个物体的初动量和末动量的量值或表达式.
注意在选取某个已知量的方向为正方向以后,凡是和选定的正方向同向的已知量取正值,反向的取负值.
(4)建立动量守恒方程,代入已知量,解出待求量,计算结果如果是正的,说明该量的方向和正方向相同,如果是负的,则和选定的正方向相反.
六、典型模型(问题):
5、多物体、多过程问题
4、碰撞问题
1、人船模型
3、小球弹簧问题
2、子弹打木块模型
x
v1
L-x
v2
例1 长为L,质量为m1小船停在静水中,一个质量为m2人,立在船头,若不计水的阻力,当人从船头走到船尾的过程中,船和人对地的位移各是多少?
解:在任一时刻,系统 总 动量都满足:
取人运动的方向为正向:
(一)、人船模型
`
`
`
`
`
`
x
L-x
一个质量为M,底面边长为b的三角形劈块静止光滑水平面上,有一质量为m的小球由斜面顶部无初速滑到底部的过程中,劈块移动的距离是多少?
解:在任一时刻,系统水平方向动量守恒:(取水平向右为正)
跟踪1
变式训练:如图所示,总质量为M的气球下端悬着质量为m的人而静止于高度为h的空中,欲使人能沿着绳安全着地,人下方的绳至少应为多长?
例2:设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,设木块对子弹的阻力恒为f,求:
1.木块至少多长子弹才不会穿出
2.子弹在木块中运动了多长时间
(二)、子弹打木块问题
(1)解:从动量的角度看,以m和M组成的系统为研究对象,根据动量守恒
对子弹用动能定理:
对木块用动能定理:
①、②相减得:
由上式可得:
……①
……②
……③
(2)以子弹为研究对象,由牛顿运动定律和运动学公式可得:
从能量的角度看,该过程系统损失的动能全部转化为系统的内能。设平均阻力大小为f,设子弹、木块的位移大小分别为s1、s2,如图所示,显然有s1-s2=L
总结:
子弹打木块的模型具有下列力学规律:
1、动力学的规律:构成系统的两物体在相互作用时,受到大小相等,方向相反的一对恒力的作用,他们的加速度大小与质量成反比,方向相反。
2、运动学的规律:在子弹进入木块的过程中,可以看成是匀减速运动,木块做匀加速运动,子弹的进入深度就是他们的相对位移。
3、动量和能量规律:系统的动量守恒,系统内各物体的动能发生变化,作用力对子弹做的功等于子弹动能的变化,作用力对木块做的功等于木块动能的变化,系统动能转化为内能,其大小等于该恒力的大小与相对位移的乘积。
A.动量守恒,机械能守恒
B.动量不守恒,机械能不守恒
C.弹性势能由最大变到最小
D.机械能由最大值变为稳定值
跟踪2 如图所示的装置中,木块B与水平桌面间的接触是光滑的,子弹A沿水平方向射入木块后留在木块内,弹簧被压缩,现将子弹、木块和弹簧合在一起作为研究系统,则此系统在从子弹开始射入到弹簧被压缩到最短的整个过程中 [ ]
(三)、小球弹簧问题
例3:如图甲所示,一轻质弹簧的两端与质量分别为m1和m2的两物块A、B相连接,并静止在光滑的水平面上.现使A瞬时获得水平向右的速度3m/s,以此刻为计时起点,两物块的速度随时间变化的规律如图乙所示,从图象信息可得( )
A.在t1、t3时刻两物块达到共同速度1m/s,且弹簧都是处于压缩状态
B.从t3到t4时刻弹簧由压缩状态恢复到原长
C.两物体的质量之比为m1:m2=1:2
D.在t2时刻A和B的动能之比为Ek1: Ek2=1:8
跟踪3:质量为m的物块甲以3m/s的速度在光滑水平面上运动,有一轻弹簧固定其上,另一质量也为m的物体乙以4m/s的速度与甲相向运动,如图所示。则( )
A.甲、乙两物块在弹簧压缩过程中,由于弹力作用,动量不守恒
B.当两物块相距最近时,甲物块的速率为零
C.当甲物块的速率为1m/s时,乙物块的速率可能为2m/s,也可能为0
D.甲物块的速率可能达到5m/s
3、碰撞三原则:
1、碰撞过程的特点:
直接作用、时间短、内力远大于外力
C、完全非弹性碰撞
2、碰撞的规律:
a、弹性碰撞
b、非弹性碰撞
a、动量守恒 b、动能不增加
C、碰撞前后要符合实际,即不可能发生第二次碰撞
(四)、碰撞问题
例4
一辆质量为M的小车以速率v1在光滑的水平面上运动时,恰遇一质量为m,速率为v2物体以俯角60。的速度方向落在车上并陷于车里的砂中,求此后车的速度。
60。
v2
v1
v’
解:系统水平方向不受外力,水平方向动量守恒:(取v2方向为正向)
例5
一个中子以2.0×107m/s的速度撞到一个静止的原子核上,已知中子以1.7 × 107m/s的速度被反弹回来,那个原子核以3.1 × 107m/s的速度向前运动,求原子核的质量数。
v
m
M
v‘
V
系统动量守恒,取v的方向为正方向:
原子核的质量数为12。
例6、质量相等的A、B两球在光滑水平面上沿一直线向同一方向运动,A球的动量为PA=7kg·m/s,B球的动量为PB =5kg·m/s,当A球追上B球发生碰撞,则碰撞后A、B两球的动量可能为( )
A.
B.
C.
D.
变式训练: 如图所示,光滑水平面上质量为m1=2kg的物块以v0=2m/s的初速冲向质量为m2=6kg静止的光滑1/4圆弧面斜劈体。求:
m1
m2
v0
5、分析与比较:下面的模型与该题的异同?
v0
1、物块m1滑到最高点位置时,二者的速度
2、 m1上升的最大高度
3、物块m1从圆弧面滑下后,二者速度
4、若m1= m2物块m1从圆弧面滑下后,二者速度
总结:解碰撞类的动量守恒注意
1、规律的应用:
动量守恒和能量守恒的综合应用。
2、注意三个制约因素:
动量守恒,能量不增加,运动要合理。
3、会情境迁移:
能把题目中的新的情境转化为自己熟悉的类型。
如图所示,A、B两木块的质量之比为3:2,原来静止在平板小车C上,A、B间有一根被压缩了的轻弹簧,A、B与平板车的上表面间的动摩擦因素相同,地面光滑。当弹簧突然释放后,A、B在小车上滑动时有:
1)A、B系统动量守恒
2)A、B、C系统动量守恒
3) 小车向左运动
4) 小车向右运动
例7
A
B
C
5、多物体、多过程问题
人和小车的总质量为M,人坐在静止于光滑水平面的小车上,以相对地的速率v 将一质量为m 的木箱沿水平面推向正前方的竖直固定挡板。设箱与挡板碰撞时无机械能损失,碰撞后箱以速率v反弹回来。人接住箱后,再以同样的相对于地的速率v 将木箱沿水平面推向正前方的挡板。已知M:m=4:1,求:
(1)人第二次推出箱后,小车和人的速度大小。
(2)人推箱多少次后不能再接到箱?
练习
解:每次推箱时,对小车、人和木箱组成的系统,动量守恒,设人和小车速度方向为正方向,每次推箱后人和小车的速度分别为v1、v2…,
则第一次推箱后:Mv1-mv=0 ⑴
第一次推箱前
第一次推箱后
解:每次推箱时,对小车、人和木箱组成的系统,动量守恒,设人和小车速度方向为正方向,每次推箱后人和小车的速度分别为v1、v2…,
第二次推箱前
第二次推箱后
第二次推箱后: Mv2-mv = (M +m )V1′ ⑶
解:每次推箱时,对小车、人和木箱组成的系统,动量守恒,设人和小车速度方向为正方向,每次推箱后人和小车的速度分别为v1、v2…,
则第一次推箱后:Mv1-mv=0 ⑴
第一次接箱后:(M +m )V1′= Mv1 + mv ⑵
第二次推箱后: Mv2-mv = (M +m )V1′ ⑶
∴v2=3mv/M
以此类推,第N次推箱后,人和小车的速度
vN=(2N-1)mv/M
当vN>v时,不再能接到箱,即
2N-1>M/m=4 N>2.5.25
∴人推箱3次后不能再接到箱
∴v1=mv/M
