2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和课件(共25张PPT)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列的前n项和课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 22:13:59 | ||
图片预览








文档简介
(共25张PPT)
等差数列的前n项和
高中数学 高二年级 选择性必修二 人教A版
南安市第三中学 杨昌座
情景引入
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
你准备怎么算呢?
情景引入
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献.
探究新知
如果数列{an} 是等差数列,p,q,s,t∈N*,且 p+q=s+t,则 ap+aq=as+at
探究新知
探究新知
思考:涉及对 n 分奇数、偶数进行讨论,较麻烦,能否设法避免分类讨论?
探究新知
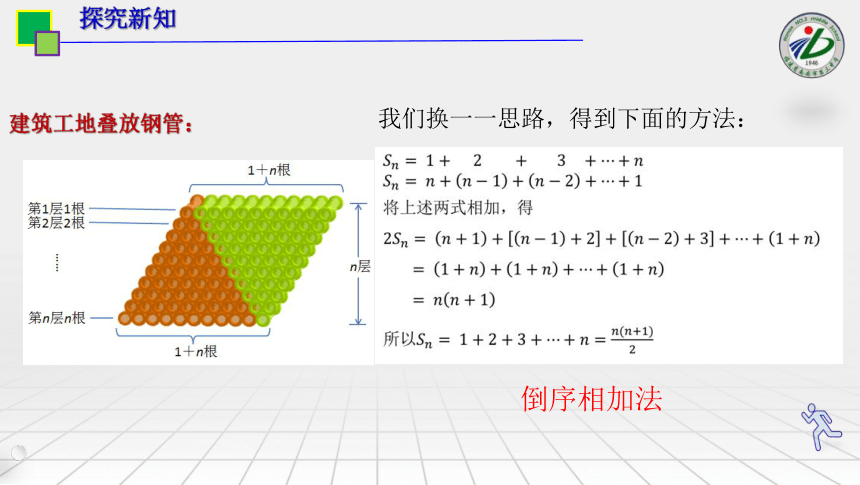
建筑工地叠放钢管:
我们换一一思路,得到下面的方法:
倒序相加法
探究新知
典型例题
归纳总结
等差数列中的基本计算
(1)利用基本量求值:
等差数列的通项公式和前n项和公式中有五个量a1,d,n,an和Sn这五个量可以“知三求二”.一般是利用公式列出基本量a1和d的方程组,解出a1和d,
便可解决问题.解题时注意整体代换的思想.
(2)结合等差数列的性质解题:等差数列的常用性质:
若m+n=p+q(m,n,p,q∈N*),则am+an=ap+aq,常与求和公式Sn 结合使用.
典型例题
一般地:
对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定。
典型例题
例8.
解:
典型例题
例9.
解:
典型例题
例9.
另解:
等差数列前n项和性质
1).将等差数列前n项和公式 看作是
一个关于n的函数,这个函数有什么特点?
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
令
(过原点)
典型例题
例10.已知等差数列{an}中,a1=13且S3=S1,求n取何值时,Sn取最大值.
典型例题
例10.已知等差数列{an}中,a1=13且S3=S1,求n取何值时,Sn取最大值.
典型例题
例10.已知等差数列{an}中,a1=13且S3=S1,求n取何值时,Sn取最大值.
典型例题
例10.已知等差数列{an}中,a1=13且S3=S1,求n取何值时,Sn取最大值.
典型例题
典型例题
典型例题
典型例题
探究新知
课后作业
等差数列的前n项和
高中数学 高二年级 选择性必修二 人教A版
南安市第三中学 杨昌座
情景引入
据说,200多年前,高斯的算术老师提出了下面的问题:
1+2+3+…+100=?
你准备怎么算呢?
情景引入
高斯(Gauss,1777-1855),德国数学家,近代数学的奠基者之一. 他在天文学、大地测量学、磁学、光学等领域都做出过杰出贡献.
探究新知
如果数列{an} 是等差数列,p,q,s,t∈N*,且 p+q=s+t,则 ap+aq=as+at
探究新知
探究新知
思考:涉及对 n 分奇数、偶数进行讨论,较麻烦,能否设法避免分类讨论?
探究新知
建筑工地叠放钢管:
我们换一一思路,得到下面的方法:
倒序相加法
探究新知
典型例题
归纳总结
等差数列中的基本计算
(1)利用基本量求值:
等差数列的通项公式和前n项和公式中有五个量a1,d,n,an和Sn这五个量可以“知三求二”.一般是利用公式列出基本量a1和d的方程组,解出a1和d,
便可解决问题.解题时注意整体代换的思想.
(2)结合等差数列的性质解题:等差数列的常用性质:
若m+n=p+q(m,n,p,q∈N*),则am+an=ap+aq,常与求和公式Sn 结合使用.
典型例题
一般地:
对于等差数列,只要给定两个相互独立的条件,这个数列就完全确定。
典型例题
例8.
解:
典型例题
例9.
解:
典型例题
例9.
另解:
等差数列前n项和性质
1).将等差数列前n项和公式 看作是
一个关于n的函数,这个函数有什么特点?
当d≠0时,Sn是常数项为零的二次函数
则 Sn=An2+Bn
令
(过原点)
典型例题
例10.已知等差数列{an}中,a1=13且S3=S1,求n取何值时,Sn取最大值.
典型例题
例10.已知等差数列{an}中,a1=13且S3=S1,求n取何值时,Sn取最大值.
典型例题
例10.已知等差数列{an}中,a1=13且S3=S1,求n取何值时,Sn取最大值.
典型例题
例10.已知等差数列{an}中,a1=13且S3=S1,求n取何值时,Sn取最大值.
典型例题
典型例题
典型例题
典型例题
探究新知
课后作业
