2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列的前项和公式第3课时(共24张PPT) 性质(2) 课件
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第二册4.2.2等差数列的前项和公式第3课时(共24张PPT) 性质(2) 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
4.2.2 等差数列的前n项和公式性质(2)
选择性必修第二册 第四章 数列
我们发现,等差数列{an}的前n项和公式 可化简为
这个函数式与函数 有什么关系?
当d=0 时,Sn的图象是一条直线上的均匀分布的点.
当d≠0 时, 是二次函数
当x = n时的函数值.
它的几何意义是一条过坐标原点的抛物线上孤立的点.
常数列
你能画出它们的图像吗?
递增或递减数列
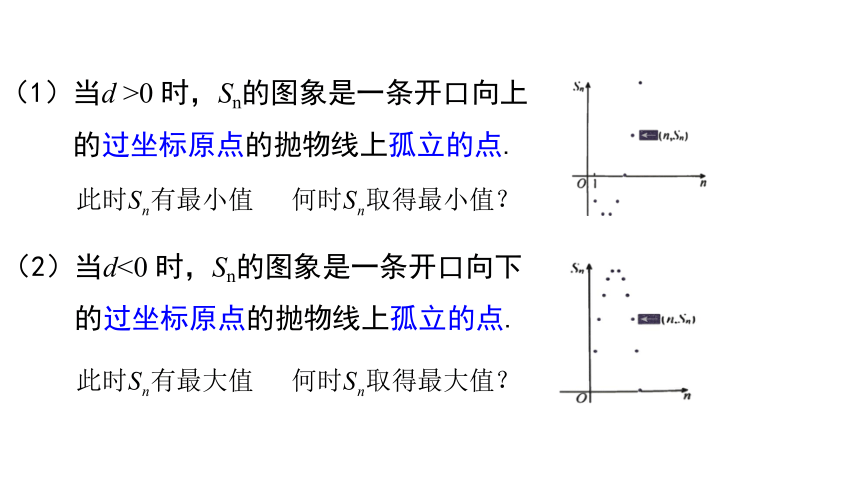
(1)当d >0 时,Sn的图象是一条开口向上
的过坐标原点的抛物线上孤立的点.
(2)当d<0 时,Sn的图象是一条开口向下
的过坐标原点的抛物线上孤立的点.
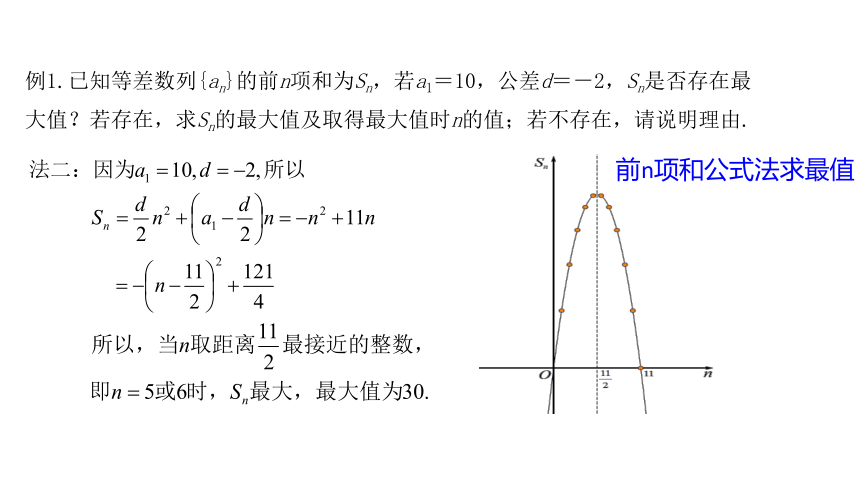
例1.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
题型一 求等差数列前n项和最值
例1.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
通项公法求最值
例1.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
前n项和公式法求最值
在等差数列中,求Sn的最小(大)值的方法:
(1)利用通项公式寻求正、负项的分界点,则从第一项起到分界点该项的各项和为最大(小).
(2)借助二次函数的图象及性质求最值.
总结归纳
练习1 在等差数列{an}中,a1=25,S17=S9,求Sn的最大值.
题型二 由前n项和公式判断数列是否是等差数列
借助等差数列定义判断是否等差
例3.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
题型三 等差数列前n项和的实际问题
题型四 含有绝对值求和
课堂小结
题型一 求等差数列前n项和最值
题型二 由前n项和公式判断数列是否是等差数列
题型三 等差数列前n项和的实际问题
题型四 含有绝对值求和
训练提升
4.2.2 等差数列的前n项和公式性质(2)
选择性必修第二册 第四章 数列
我们发现,等差数列{an}的前n项和公式 可化简为
这个函数式与函数 有什么关系?
当d=0 时,Sn的图象是一条直线上的均匀分布的点.
当d≠0 时, 是二次函数
当x = n时的函数值.
它的几何意义是一条过坐标原点的抛物线上孤立的点.
常数列
你能画出它们的图像吗?
递增或递减数列
(1)当d >0 时,Sn的图象是一条开口向上
的过坐标原点的抛物线上孤立的点.
(2)当d<0 时,Sn的图象是一条开口向下
的过坐标原点的抛物线上孤立的点.
例1.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
题型一 求等差数列前n项和最值
例1.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
通项公法求最值
例1.已知等差数列{an}的前n项和为Sn,若a1=10,公差d=-2,Sn是否存在最大值?若存在,求Sn的最大值及取得最大值时n的值;若不存在,请说明理由.
前n项和公式法求最值
在等差数列中,求Sn的最小(大)值的方法:
(1)利用通项公式寻求正、负项的分界点,则从第一项起到分界点该项的各项和为最大(小).
(2)借助二次函数的图象及性质求最值.
总结归纳
练习1 在等差数列{an}中,a1=25,S17=S9,求Sn的最大值.
题型二 由前n项和公式判断数列是否是等差数列
借助等差数列定义判断是否等差
例3.某校新建一个报告厅,要求容纳800个座位,报告厅共有20排座位,从第2排起后一排都比前一排多两个座位. 问第1排应安排多少个座位?
题型三 等差数列前n项和的实际问题
题型四 含有绝对值求和
课堂小结
题型一 求等差数列前n项和最值
题型二 由前n项和公式判断数列是否是等差数列
题型三 等差数列前n项和的实际问题
题型四 含有绝对值求和
训练提升
