2021-2022学年北师大版九年级数学下册3.1圆 辅导训练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.1圆 辅导训练 (Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 262.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 09:33:22 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学下册《3.1圆》优生辅导训练(附答案)
1.如图,⊙O的直径AB与弦CD的延长线交于点E,若OB=DE,∠E=26°,则∠AOC是( )
A.52° B.62° C.72° D.78°
2.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
3.点M,N是⊙O上两点,已知OM=3cm,那么一定有( )
A.MN>6cm B.MN=6cm C.MN≤6cm D.MN<6cm
4.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
5.已知,如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
6.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
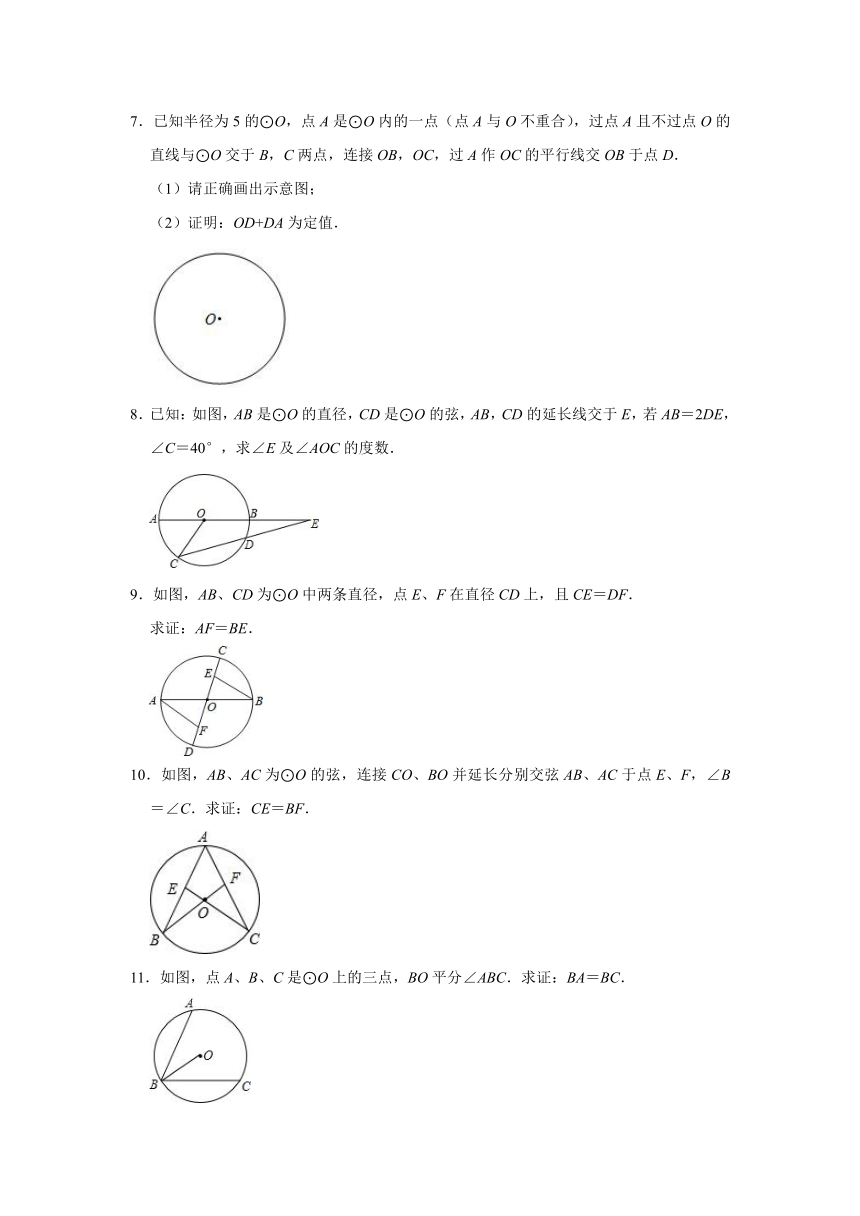
7.已知半径为5的⊙O,点A是⊙O内的一点(点A与O不重合),过点A且不过点O的直线与⊙O交于B,C两点,连接OB,OC,过A作OC的平行线交OB于点D.
(1)请正确画出示意图;
(2)证明:OD+DA为定值.
8.已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠C=40°,求∠E及∠AOC的度数.
9.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
10.如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.
11.如图,点A、B、C是⊙O上的三点,BO平分∠ABC.求证:BA=BC.
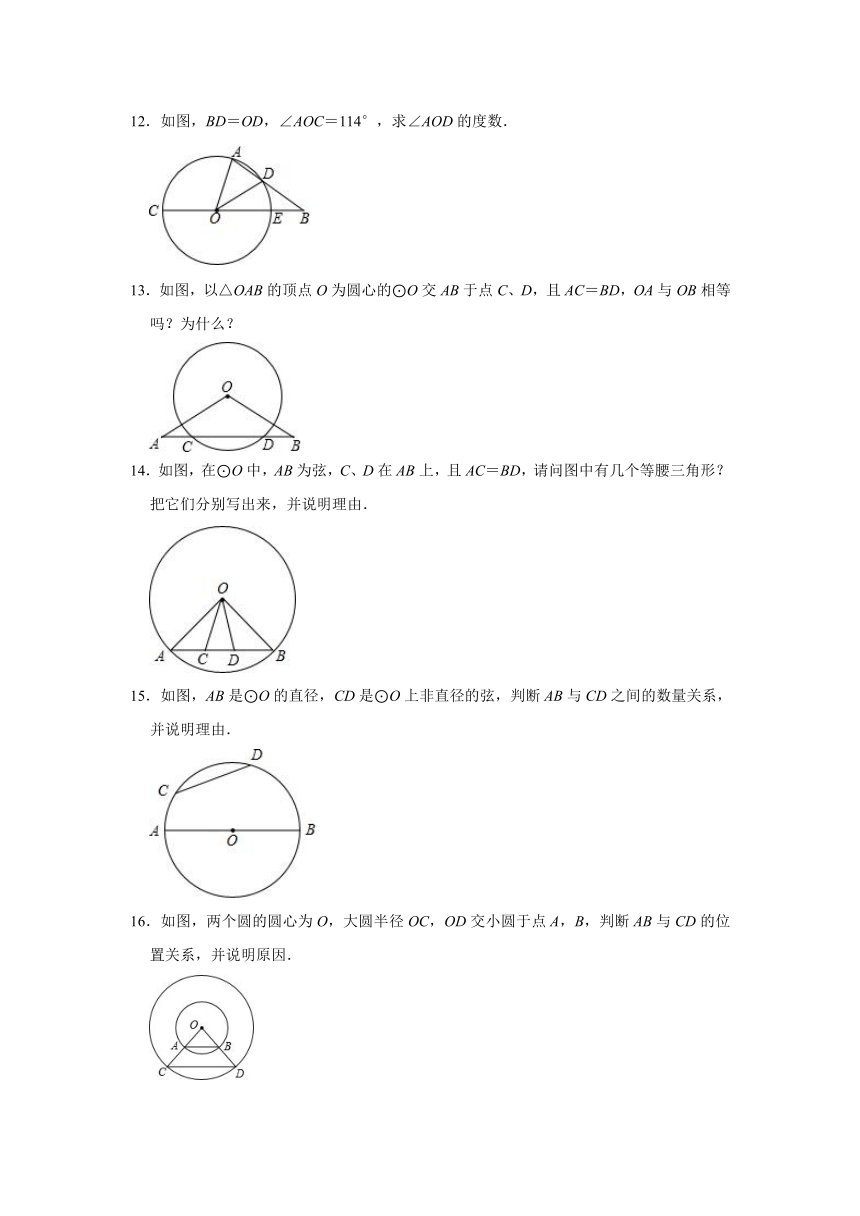
12.如图,BD=OD,∠AOC=114°,求∠AOD的度数.
13.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD,OA与OB相等吗?为什么?
14.如图,在⊙O中,AB为弦,C、D在AB上,且AC=BD,请问图中有几个等腰三角形?把它们分别写出来,并说明理由.
15.如图,AB是⊙O的直径,CD是⊙O上非直径的弦,判断AB与CD之间的数量关系,并说明理由.
16.如图,两个圆的圆心为O,大圆半径OC,OD交小圆于点A,B,判断AB与CD的位置关系,并说明原因.
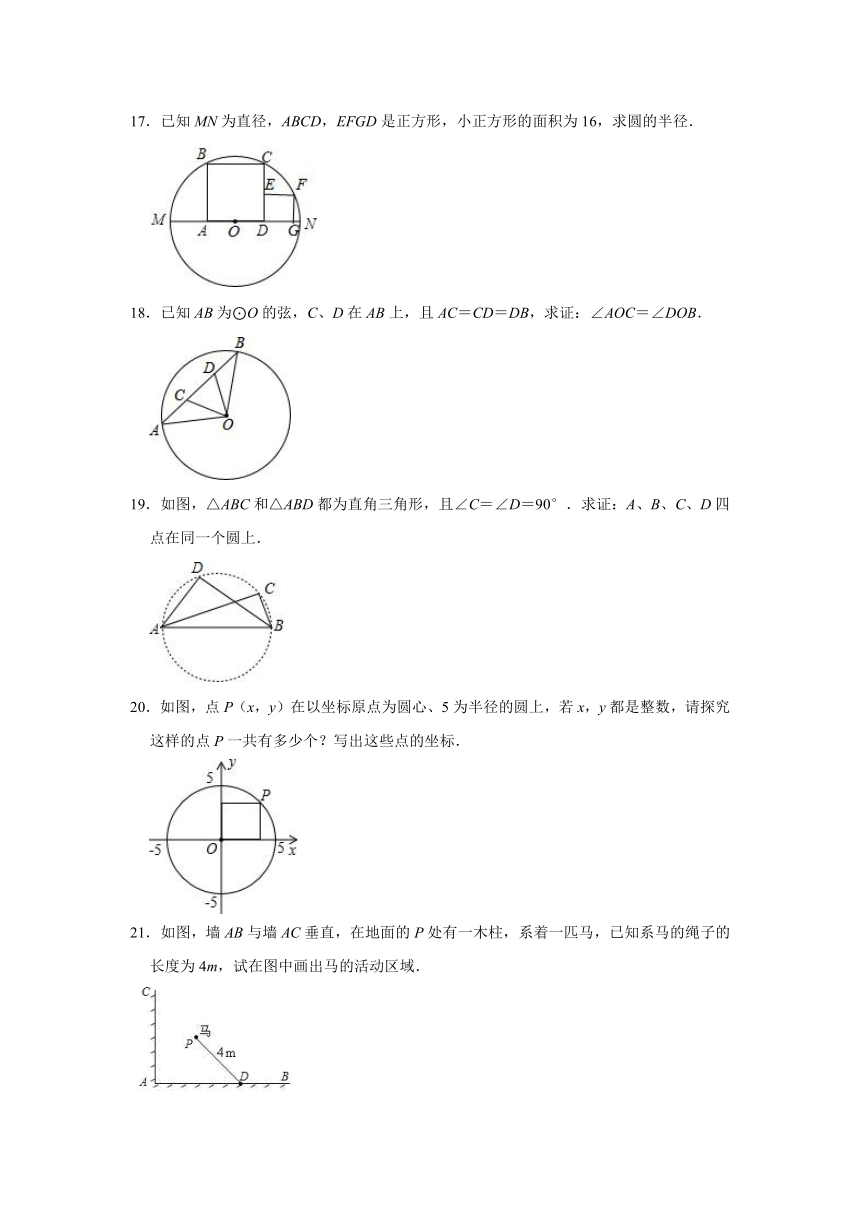
17.已知MN为直径,ABCD,EFGD是正方形,小正方形的面积为16,求圆的半径.
18.已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
19.如图,△ABC和△ABD都为直角三角形,且∠C=∠D=90°.求证:A、B、C、D四点在同一个圆上.
20.如图,点P(x,y)在以坐标原点为圆心、5为半径的圆上,若x,y都是整数,请探究这样的点P一共有多少个?写出这些点的坐标.
如图,墙AB与墙AC垂直,在地面的P处有一木柱,系着一匹马,已知系马的绳子的长度为4m,试在图中画出马的活动区域.
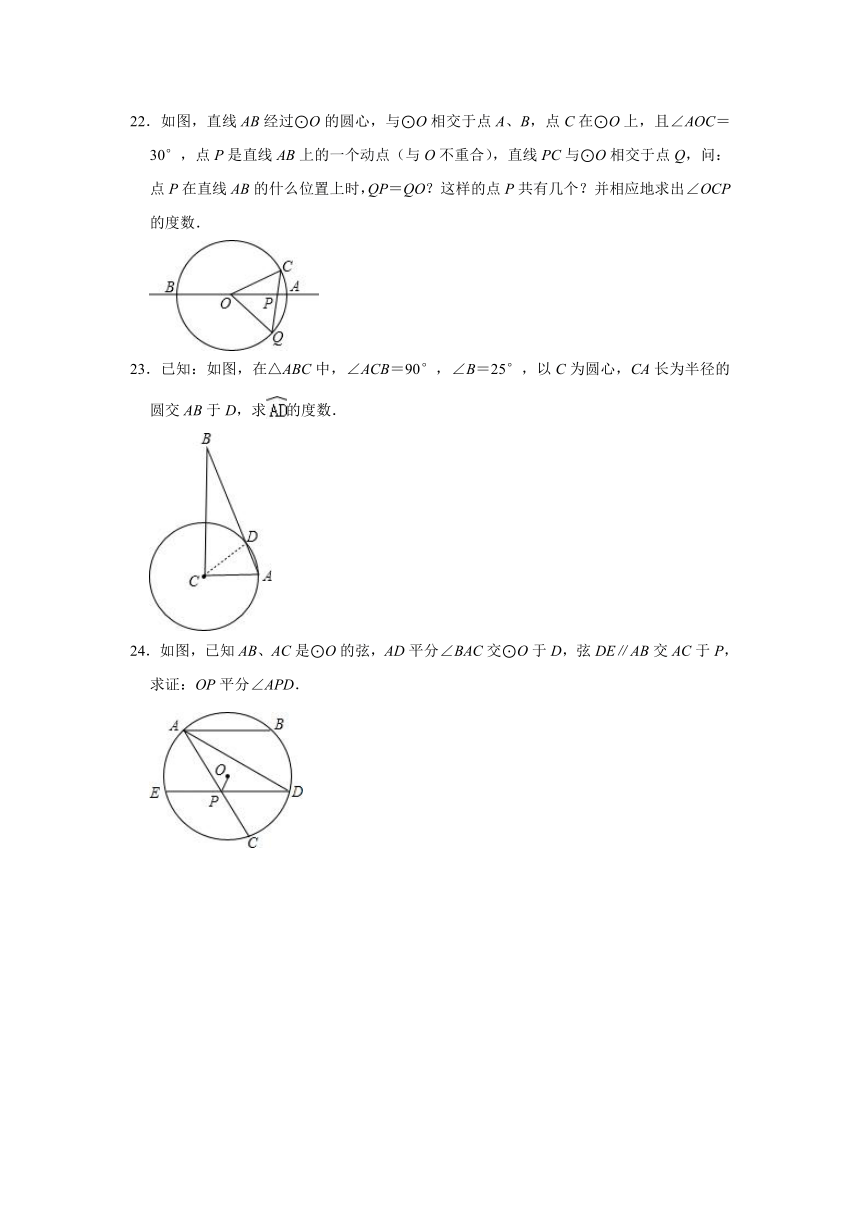
22.如图,直线AB经过⊙O的圆心,与⊙O相交于点A、B,点C在⊙O上,且∠AOC=30°,点P是直线AB上的一个动点(与O不重合),直线PC与⊙O相交于点Q,问:点P在直线AB的什么位置上时,QP=QO?这样的点P共有几个?并相应地求出∠OCP的度数.
23.已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA长为半径的圆交AB于D,求的度数.
24.如图,已知AB、AC是⊙O的弦,AD平分∠BAC交⊙O于D,弦DE∥AB交AC于P,求证:OP平分∠APD.
参考答案
1.解:连接OD,如图,
∵OD=OB=DE,
∴∠DOE=∠E=26°,
∴∠ODC=∠DOE+∠E=26°+26°=52°,
∵OC=OD,
∴∠C=∠ODC=52°,
∴∠AOC=∠C+∠E=52°+26°=78°.
故选:D.
2.解:如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,BD=OC=OA=10,
∴OB===6,
∴AB=OA﹣OB=4,
故选:C.
3.解:∵M、N是⊙O上两点,OM=3cm,
∴圆的半径为3cm,圆的直径为6cm,
∴MN≤6cm.
故选:C.
4.证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
5.解:∵OA、OB是⊙O的两条半径,
∴AO=BO,
∵C、D分别是半径OA、BO的中点,
∴OC=OD,
在△OCB和△ODA中,
,
∴△OCB≌△ODA(SAS),
∴AD=BC.
6.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
7.解:(1)如图所示:
(2)∵AD∥OC,
∴△ABD∽△CBO,
∴,
∵OB=OC=5,
∴,
可得:OD+DA=5,
即OD+DA为定值.
8.解:连接OD,
∵OC=OD,∠C=40°,
∴∠ODC=∠C=40°,
∵AB=2DE,OD=AB,
∴OD=DE,
∵∠ODC是△DOE的外角,
∴∠E=∠EOD=∠ODC=20°,
∵∠AOC是△COE的外角,
∴∠AOC=∠C+∠E=40°+20°=60°.
9.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
10.证明:∵在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),
∴OE=OF,
又∵OB=OC
∴CE=BF.
11.证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
12.解:设∠B=x,
∵BD=OD,
∴∠DOB=∠B=x,
∴∠ADO=∠DOB+∠B=2x,
∵OA=OD,
∴∠A=∠ADO=2x,
∵∠AOC=∠A+∠B,
∴2x+x=114°,解得x=38°,
∴∠AOD=180°﹣∠OAD﹣∠ADO=180°﹣4x=180°﹣4×38°=28°.
13.答:OA=OB.
理由如下:
如图,过O作OE⊥AB于E,
∵CD是⊙O的弦,OE⊥CD,
∴CE=DE,
∵AC=BD,
∴AE=BE,
∵OE⊥CD,
∴OA=OB.
14.解:等腰三角形有:△OAB、△OCD.
证明:∵OA=OB(同圆半径相等),
∴△OAB是等腰三角形,
∴∠A=∠B,
又∵AC=BD,OA=OB,
∴△OAC≌△OBD,
∴OC=OD,
∴△OCD是等腰三角形.
15.解:AB>CD,
因为AB是圆的直径,长度大于所有的非直径的弦.
16.解:AB∥CD.
∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∴∠OAB=(180°﹣∠O),∠OCD=(180°﹣∠O),
∴∠OAB=∠OCD,
∴AB∥CD.
17.解:连接OC、OF,
设AD=2x,
∵CO2=DO2+CD2,
∴x2+(2x)2=r2,
∵OF2=OG2+FG2,
∴r2=(x+4)2+42=x2+8x+32,
∴x2+(2x)2=x2+8x+32,
解得:x1=4,x2=﹣2(舍去),
∴r2=5×42,
r=4.
18.证明:∵OA=OB,
∴∠A=∠B,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴∠AOC=∠DOB.
19.证明:取AB的中点O,连接OC,OD,
∵△ABC和△ABD都为直角三角形,且∠C=∠D=90°
∴DO,CO分别为Rt△ABD和Rt△ABC斜边上的中线,
∴OA=OB=OC=OD.
∴A、B、C、D四点在同一个圆上.
20.解:分为两种情况:
①若这个点在坐标轴上,那么有四个,它们是(0,5),(5,0),(﹣5,0),(0,﹣5);
②若这个点在象限内,
∵52=42+32,而P都是整数点,
∴这样的点有8个,分别是(3,4),(﹣3,4),(3,﹣4),(﹣3,﹣4),(4,3)(﹣4,3),(4,﹣3 ),(﹣4,﹣3),
∴这些点的坐标共有12个.
21.解:作法:以p为圆心,以4米长为半径画一条与两墙均相交的弧.
22.解:①根据题意,画出图①,
在△QOC中,OC=OQ,
∴∠OQC=∠OCQ,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠QPO=∠OCQ+∠AOC,∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图②)
∵OC=OQ,∴∠OQP=①,
∵OQ=PQ,
∴∠OPQ=②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图③),
∵OC=OQ,
∴∠OCP=∠OQC=①,
∵OQ=PQ,
∴∠P=②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
综上所述,∠OCP=180°﹣150°﹣10°=20°.
23.解:∵在△ABC中,∠ACB=90°,∠B=25°
∴∠A=90°﹣∠B=65度.
∵CA=CD
∴∠CDA=∠CAD=65°
∴∠ACD=50°
即弧AD的度数是50度.
24.证明:作OM⊥AC于M,ON⊥DE于N,如图,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵CD弧=BD弧,
∵DE∥AB,
∴∠ADE=∠BAD,
∴AE弧=BD弧,
∴AE弧=CD弧,
∴AE弧+EC弧=EC弧+CD弧,即AC弧=ED弧,
∴AC=DE,
∴OM=ON,
∴OP平分∠APD.
1.如图,⊙O的直径AB与弦CD的延长线交于点E,若OB=DE,∠E=26°,则∠AOC是( )
A.52° B.62° C.72° D.78°
2.如图,OA是⊙O的半径,B为OA上一点(且不与点O、A重合),过点B作OA的垂线交⊙O于点C.以OB、BC为边作矩形OBCD,连接BD.若BD=10,BC=8,则AB的长为( )
A.8 B.6 C.4 D.2
3.点M,N是⊙O上两点,已知OM=3cm,那么一定有( )
A.MN>6cm B.MN=6cm C.MN≤6cm D.MN<6cm
4.已知:如图,BD、CE是△ABC的高,M为BC的中点.试说明点B、C、D、E在以点M为圆心的同一个圆上.
5.已知,如图,在⊙O中,C、D分别是半径OA、BO的中点,求证:AD=BC.
6.已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?
7.已知半径为5的⊙O,点A是⊙O内的一点(点A与O不重合),过点A且不过点O的直线与⊙O交于B,C两点,连接OB,OC,过A作OC的平行线交OB于点D.
(1)请正确画出示意图;
(2)证明:OD+DA为定值.
8.已知:如图,AB是⊙O的直径,CD是⊙O的弦,AB,CD的延长线交于E,若AB=2DE,∠C=40°,求∠E及∠AOC的度数.
9.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
10.如图,AB、AC为⊙O的弦,连接CO、BO并延长分别交弦AB、AC于点E、F,∠B=∠C.求证:CE=BF.
11.如图,点A、B、C是⊙O上的三点,BO平分∠ABC.求证:BA=BC.
12.如图,BD=OD,∠AOC=114°,求∠AOD的度数.
13.如图,以△OAB的顶点O为圆心的⊙O交AB于点C、D,且AC=BD,OA与OB相等吗?为什么?
14.如图,在⊙O中,AB为弦,C、D在AB上,且AC=BD,请问图中有几个等腰三角形?把它们分别写出来,并说明理由.
15.如图,AB是⊙O的直径,CD是⊙O上非直径的弦,判断AB与CD之间的数量关系,并说明理由.
16.如图,两个圆的圆心为O,大圆半径OC,OD交小圆于点A,B,判断AB与CD的位置关系,并说明原因.
17.已知MN为直径,ABCD,EFGD是正方形,小正方形的面积为16,求圆的半径.
18.已知AB为⊙O的弦,C、D在AB上,且AC=CD=DB,求证:∠AOC=∠DOB.
19.如图,△ABC和△ABD都为直角三角形,且∠C=∠D=90°.求证:A、B、C、D四点在同一个圆上.
20.如图,点P(x,y)在以坐标原点为圆心、5为半径的圆上,若x,y都是整数,请探究这样的点P一共有多少个?写出这些点的坐标.
如图,墙AB与墙AC垂直,在地面的P处有一木柱,系着一匹马,已知系马的绳子的长度为4m,试在图中画出马的活动区域.
22.如图,直线AB经过⊙O的圆心,与⊙O相交于点A、B,点C在⊙O上,且∠AOC=30°,点P是直线AB上的一个动点(与O不重合),直线PC与⊙O相交于点Q,问:点P在直线AB的什么位置上时,QP=QO?这样的点P共有几个?并相应地求出∠OCP的度数.
23.已知:如图,在△ABC中,∠ACB=90°,∠B=25°,以C为圆心,CA长为半径的圆交AB于D,求的度数.
24.如图,已知AB、AC是⊙O的弦,AD平分∠BAC交⊙O于D,弦DE∥AB交AC于P,求证:OP平分∠APD.
参考答案
1.解:连接OD,如图,
∵OD=OB=DE,
∴∠DOE=∠E=26°,
∴∠ODC=∠DOE+∠E=26°+26°=52°,
∵OC=OD,
∴∠C=∠ODC=52°,
∴∠AOC=∠C+∠E=52°+26°=78°.
故选:D.
2.解:如图,连接OC.
∵四边形OBCD是矩形,
∴∠OBC=90°,BD=OC=OA=10,
∴OB===6,
∴AB=OA﹣OB=4,
故选:C.
3.解:∵M、N是⊙O上两点,OM=3cm,
∴圆的半径为3cm,圆的直径为6cm,
∴MN≤6cm.
故选:C.
4.证明:连接ME、MD,
∵BD、CE分别是△ABC的高,M为BC的中点,
∴ME=MD=MC=MB=BC,
∴点B、C、D、E在以点M为圆心的同一圆上.
5.解:∵OA、OB是⊙O的两条半径,
∴AO=BO,
∵C、D分别是半径OA、BO的中点,
∴OC=OD,
在△OCB和△ODA中,
,
∴△OCB≌△ODA(SAS),
∴AD=BC.
6.解:AC与BD相等.理由如下:
连接OC、OD,如图,
∵OA=OB,AE=BF,
∴OE=OF,
∵CE⊥AB,DF⊥AB,
∴∠OEC=∠OFD=90°,
在Rt△OEC和Rt△OFD中,
,
∴Rt△OEC≌Rt△OFD(HL),
∴∠COE=∠DOF,
∴=,
∴AC=BD.
7.解:(1)如图所示:
(2)∵AD∥OC,
∴△ABD∽△CBO,
∴,
∵OB=OC=5,
∴,
可得:OD+DA=5,
即OD+DA为定值.
8.解:连接OD,
∵OC=OD,∠C=40°,
∴∠ODC=∠C=40°,
∵AB=2DE,OD=AB,
∴OD=DE,
∵∠ODC是△DOE的外角,
∴∠E=∠EOD=∠ODC=20°,
∵∠AOC是△COE的外角,
∴∠AOC=∠C+∠E=40°+20°=60°.
9.解:∵AB、CD为⊙O中两条直径,
∴OA=OB,OC=OD,
∵CE=DF,
∴OE=OF,
在△AOF和△BOE中,
,
∴△AOF≌△BOE(SAS),
∴AF=BE.
10.证明:∵在△BOE和△COF中,
,
∴△BOE≌△COF(ASA),
∴OE=OF,
又∵OB=OC
∴CE=BF.
11.证明:连OA、OC,如图,
∵OA=OB,OB=OC,
∴∠ABO=∠BAO,∠CBO=∠BCO,
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∴∠BAO=∠BCO,
∴△OAB≌△OCB,
∴AB=BC.
12.解:设∠B=x,
∵BD=OD,
∴∠DOB=∠B=x,
∴∠ADO=∠DOB+∠B=2x,
∵OA=OD,
∴∠A=∠ADO=2x,
∵∠AOC=∠A+∠B,
∴2x+x=114°,解得x=38°,
∴∠AOD=180°﹣∠OAD﹣∠ADO=180°﹣4x=180°﹣4×38°=28°.
13.答:OA=OB.
理由如下:
如图,过O作OE⊥AB于E,
∵CD是⊙O的弦,OE⊥CD,
∴CE=DE,
∵AC=BD,
∴AE=BE,
∵OE⊥CD,
∴OA=OB.
14.解:等腰三角形有:△OAB、△OCD.
证明:∵OA=OB(同圆半径相等),
∴△OAB是等腰三角形,
∴∠A=∠B,
又∵AC=BD,OA=OB,
∴△OAC≌△OBD,
∴OC=OD,
∴△OCD是等腰三角形.
15.解:AB>CD,
因为AB是圆的直径,长度大于所有的非直径的弦.
16.解:AB∥CD.
∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∴∠OAB=(180°﹣∠O),∠OCD=(180°﹣∠O),
∴∠OAB=∠OCD,
∴AB∥CD.
17.解:连接OC、OF,
设AD=2x,
∵CO2=DO2+CD2,
∴x2+(2x)2=r2,
∵OF2=OG2+FG2,
∴r2=(x+4)2+42=x2+8x+32,
∴x2+(2x)2=x2+8x+32,
解得:x1=4,x2=﹣2(舍去),
∴r2=5×42,
r=4.
18.证明:∵OA=OB,
∴∠A=∠B,
在△OAC和△OBD中,
,
∴△OAC≌△OBD(SAS),
∴∠AOC=∠DOB.
19.证明:取AB的中点O,连接OC,OD,
∵△ABC和△ABD都为直角三角形,且∠C=∠D=90°
∴DO,CO分别为Rt△ABD和Rt△ABC斜边上的中线,
∴OA=OB=OC=OD.
∴A、B、C、D四点在同一个圆上.
20.解:分为两种情况:
①若这个点在坐标轴上,那么有四个,它们是(0,5),(5,0),(﹣5,0),(0,﹣5);
②若这个点在象限内,
∵52=42+32,而P都是整数点,
∴这样的点有8个,分别是(3,4),(﹣3,4),(3,﹣4),(﹣3,﹣4),(4,3)(﹣4,3),(4,﹣3 ),(﹣4,﹣3),
∴这些点的坐标共有12个.
21.解:作法:以p为圆心,以4米长为半径画一条与两墙均相交的弧.
22.解:①根据题意,画出图①,
在△QOC中,OC=OQ,
∴∠OQC=∠OCQ,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠QPO=∠OCQ+∠AOC,∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图②)
∵OC=OQ,∴∠OQP=①,
∵OQ=PQ,
∴∠OPQ=②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图③),
∵OC=OQ,
∴∠OCP=∠OQC=①,
∵OQ=PQ,
∴∠P=②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
综上所述,∠OCP=180°﹣150°﹣10°=20°.
23.解:∵在△ABC中,∠ACB=90°,∠B=25°
∴∠A=90°﹣∠B=65度.
∵CA=CD
∴∠CDA=∠CAD=65°
∴∠ACD=50°
即弧AD的度数是50度.
24.证明:作OM⊥AC于M,ON⊥DE于N,如图,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵CD弧=BD弧,
∵DE∥AB,
∴∠ADE=∠BAD,
∴AE弧=BD弧,
∴AE弧=CD弧,
∴AE弧+EC弧=EC弧+CD弧,即AC弧=ED弧,
∴AC=DE,
∴OM=ON,
∴OP平分∠APD.
