2021-2022学年北师大版九年级数学上册3.2 用频率估计概率 复习练习题 (Word版含简答)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册3.2 用频率估计概率 复习练习题 (Word版含简答) |  | |
| 格式 | doc | ||
| 文件大小 | 96.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 09:33:27 | ||
图片预览


文档简介
3.2 用频率估计概率
一、选择题
1.关于频率与概率的关系,下列说法中正确的是( )
A.频率等于概率
B.当试验次数很大时,频率稳定在概率的附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
2.在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次,50次,100次,200次,其中试验相对科学的是( )
A.甲组 B.乙组 C.丙组 D.丁组
3. 做重复试验:抛掷同一枚啤酒瓶盖1000次,经过统计得“凸面向上”的频率约为0.44,则可以由此估计抛掷啤酒瓶盖出现“凹面向上”的概率约为( )
A.0.22 B.0.44 C.0.50 D.0.56
4. 一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.20 B.24 C.28 D.30
5.在一个不透明的盒子中装有8个白球,若干个黄球,它们除颜色不同外,其余均相同,若从中随机摸一个球,它是白球的概率为,则黄球的个数是( )
A.2 B.4 C.12 D.16
6.抛一枚均匀的硬币,出现正面和反面朝上的概率相等,则下列说法正确的是( )
A.若抛20000次一定会有10000次出现正面
B.若抛20000次一定小于10000次出现正面
C.若抛20000次出现正面和反面的次数都非常接近10000次
D.若抛20000次出现正面和反面的次数无法预料
7.某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
二、填空题
8. 事件发生的频率随着试验次数的增加,逐渐稳定在某个数值附近,我们可以用平衡时的 来估计这一事件的 .
9. 通过试验的方法用频率去估计概率的大小,必须要求试验在 条件下进行,试验的次数越 就越有可能得到较准的估计值.
10. 某市一出租车公司共有300辆出租车,某人统计他一天中遇到的1000辆出租车共有60辆是该公司的车,则估计该市共约有 辆出租车.
11. 色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
抽取的体检表数n 50 100 200 400 500 800 1000 1200 1500 2000
色盲患者的频数m 3 7 13 29 37 55 69 85 105 138
色盲患者的频率m/n 0.060 0.070 0.065 0.073 0.074 0.069 0.069 0.071 0.070 0.069
根据表中数据,估计在男性中,男性患色盲的概率为 (结果精确到0.01).
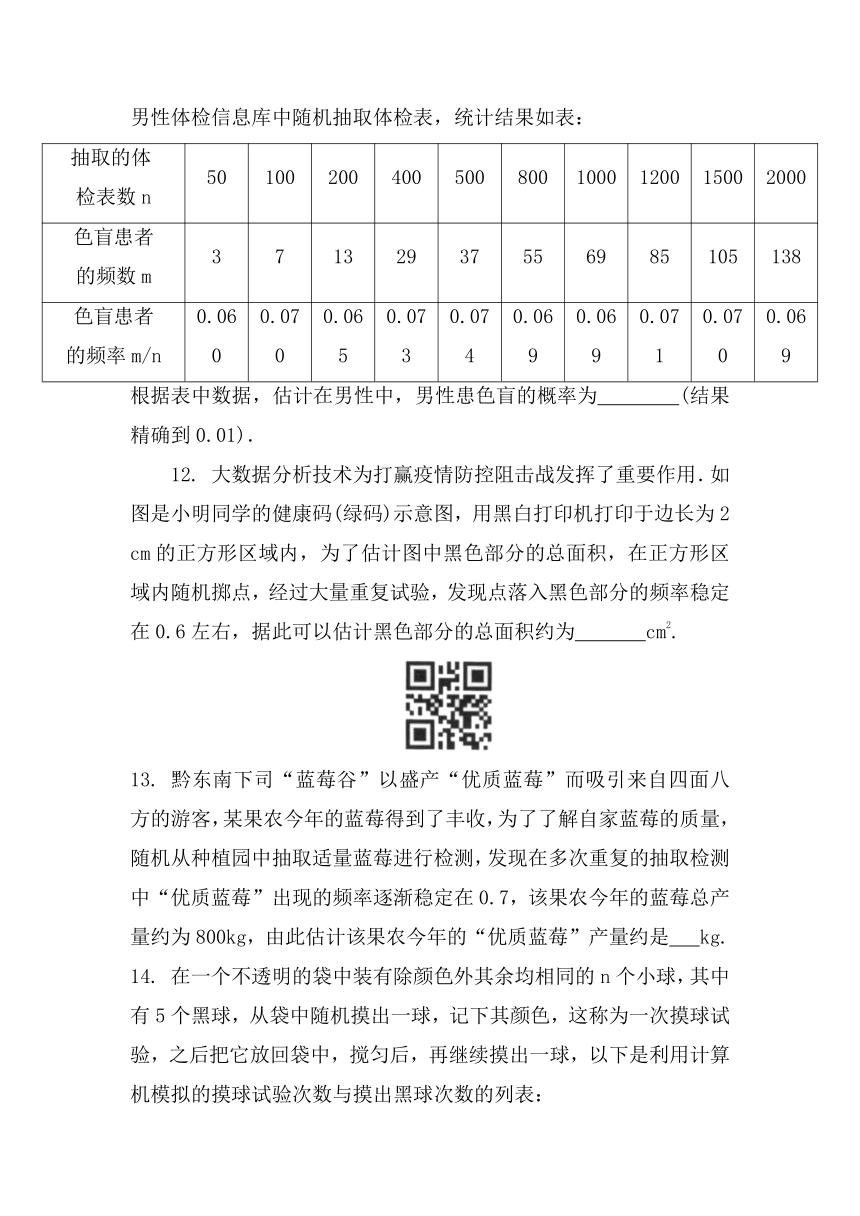
12. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为2 cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 cm2.
13. 黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客,某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800kg,由此估计该果农今年的“优质蓝莓”产量约是 kg.
14. 在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数 100 1000 5000 10000 50000 100000
摸出黑球次数 46 487 2506 5008 24996 50007
根据列表,可以估计出n的值是 .
三、解答题
15. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 65 124 178 302 481 599 1803
摸到白球的频率m/n 0.65 0.62 0.593 0.604 0.601 0.599 0.601
(1) 请估计:当n很大时,摸到白球的频率将会接近 (精确到0.1);
(2) 假如你摸一次,你摸到白球的概率P(白球)= ;
(3) 试估算盒子里黑、白两种颜色的球各有多少个?
16. 小强与小刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数 1 2 3 4 5 6
出现次数 6 9 5 8 16 10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)小强说:“根据试验,一次试验中出现向上点数为5的概率最大.”小刚说:“如果抛了540次,那么出现向上点数为6的次数正好是100次.”请判断小强与小刚说法的对错.
17. 新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度人数方式 0.2~0.4 0.4~0.6 0.6~0.8 0.8~1
录播 4 16 12 8
直播 2 10 16 12
(1) 你认为哪种教学方式学生的参与度更高?简要说明理由;
(2) 从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3) 该校共有800名学生,选择“录播”和“直播”的人数之比为1∶3,估计参与度在0.4以下的共有多少人?
答案:
一、
1-7 BDDDB CD
二、
8. 频率 概率
9. 相同 越多
10. 5000
11. 0.07
12. 2.4
13. 560
14. 10
三、
15. (1) 0.6
(2) 0.6
(3) 解:黑球个数为40×0.4=16(个),白球40×0.6=24(个).
16. 解:(1) 向上点数为3的频率为;向上点数为5的频率为=;
(2) 小强的说法错误,因为频率最大并不能说明概率最大,只有试验的次数很大时,该事件发生的频率稳定在相应的概率附近;小刚的说法错误,因为事件发生具有随机性,次数不一定是100次.
17. 解:(1)“直播”教学方式学生的参与度更高.理由如下:∵直播参与度为“0.6~0.8”“0.8~1”的人数均大于录播参与度的人数,故“直播”教学方式学生的参与度更高;
(2)P(参与度在0.8及以上)=×100%=30%;
(3)该校共有800名学生,选择“录播”的人数为800×=200(人),选择“直播”的人数为800×=600(人),故参与度在0.4以下的共有200×+600×=20+30=50(人).
一、选择题
1.关于频率与概率的关系,下列说法中正确的是( )
A.频率等于概率
B.当试验次数很大时,频率稳定在概率的附近
C.当试验次数很大时,概率稳定在频率附近
D.试验得到的频率与概率不可能相等
2.在课外实践活动中,甲、乙、丙、丁四个小组用投掷一元硬币的方法估算正面朝上的概率,其实验次数分别为10次,50次,100次,200次,其中试验相对科学的是( )
A.甲组 B.乙组 C.丙组 D.丁组
3. 做重复试验:抛掷同一枚啤酒瓶盖1000次,经过统计得“凸面向上”的频率约为0.44,则可以由此估计抛掷啤酒瓶盖出现“凹面向上”的概率约为( )
A.0.22 B.0.44 C.0.50 D.0.56
4. 一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有9个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么估计盒子中小球的个数n为( )
A.20 B.24 C.28 D.30
5.在一个不透明的盒子中装有8个白球,若干个黄球,它们除颜色不同外,其余均相同,若从中随机摸一个球,它是白球的概率为,则黄球的个数是( )
A.2 B.4 C.12 D.16
6.抛一枚均匀的硬币,出现正面和反面朝上的概率相等,则下列说法正确的是( )
A.若抛20000次一定会有10000次出现正面
B.若抛20000次一定小于10000次出现正面
C.若抛20000次出现正面和反面的次数都非常接近10000次
D.若抛20000次出现正面和反面的次数无法预料
7.某小组做“用频率估计概率”的试验时,绘出的某一结果出现的频率折线图,则符合这一结果的试验可能是( )
A.抛一枚硬币,出现正面朝上
B.掷一个正六面体的骰子,出现3点朝上
C.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D.从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
二、填空题
8. 事件发生的频率随着试验次数的增加,逐渐稳定在某个数值附近,我们可以用平衡时的 来估计这一事件的 .
9. 通过试验的方法用频率去估计概率的大小,必须要求试验在 条件下进行,试验的次数越 就越有可能得到较准的估计值.
10. 某市一出租车公司共有300辆出租车,某人统计他一天中遇到的1000辆出租车共有60辆是该公司的车,则估计该市共约有 辆出租车.
11. 色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
抽取的体检表数n 50 100 200 400 500 800 1000 1200 1500 2000
色盲患者的频数m 3 7 13 29 37 55 69 85 105 138
色盲患者的频率m/n 0.060 0.070 0.065 0.073 0.074 0.069 0.069 0.071 0.070 0.069
根据表中数据,估计在男性中,男性患色盲的概率为 (结果精确到0.01).
12. 大数据分析技术为打赢疫情防控阻击战发挥了重要作用.如图是小明同学的健康码(绿码)示意图,用黑白打印机打印于边长为2 cm的正方形区域内,为了估计图中黑色部分的总面积,在正方形区域内随机掷点,经过大量重复试验,发现点落入黑色部分的频率稳定在0.6左右,据此可以估计黑色部分的总面积约为 cm2.
13. 黔东南下司“蓝莓谷”以盛产“优质蓝莓”而吸引来自四面八方的游客,某果农今年的蓝莓得到了丰收,为了了解自家蓝莓的质量,随机从种植园中抽取适量蓝莓进行检测,发现在多次重复的抽取检测中“优质蓝莓”出现的频率逐渐稳定在0.7,该果农今年的蓝莓总产量约为800kg,由此估计该果农今年的“优质蓝莓”产量约是 kg.
14. 在一个不透明的袋中装有除颜色外其余均相同的n个小球,其中有5个黑球,从袋中随机摸出一球,记下其颜色,这称为一次摸球试验,之后把它放回袋中,搅匀后,再继续摸出一球,以下是利用计算机模拟的摸球试验次数与摸出黑球次数的列表:
摸球试验次数 100 1000 5000 10000 50000 100000
摸出黑球次数 46 487 2506 5008 24996 50007
根据列表,可以估计出n的值是 .
三、解答题
15. 在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n 100 200 300 500 800 1000 3000
摸到白球的次数m 65 124 178 302 481 599 1803
摸到白球的频率m/n 0.65 0.62 0.593 0.604 0.601 0.599 0.601
(1) 请估计:当n很大时,摸到白球的频率将会接近 (精确到0.1);
(2) 假如你摸一次,你摸到白球的概率P(白球)= ;
(3) 试估算盒子里黑、白两种颜色的球各有多少个?
16. 小强与小刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数 1 2 3 4 5 6
出现次数 6 9 5 8 16 10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率;
(2)小强说:“根据试验,一次试验中出现向上点数为5的概率最大.”小刚说:“如果抛了540次,那么出现向上点数为6的次数正好是100次.”请判断小强与小刚说法的对错.
17. 新冠疫情期间,某校开展线上教学,有“录播”和“直播”两种教学方式供学生选择其中一种.为分析该校学生线上学习情况,在接受这两种教学方式的学生中各随机抽取40人调查学习参与度,数据整理结果如表(数据分组包含左端值不包含右端值).
参与度人数方式 0.2~0.4 0.4~0.6 0.6~0.8 0.8~1
录播 4 16 12 8
直播 2 10 16 12
(1) 你认为哪种教学方式学生的参与度更高?简要说明理由;
(2) 从教学方式为“直播”的学生中任意抽取一位学生,估计该学生的参与度在0.8及以上的概率是多少?
(3) 该校共有800名学生,选择“录播”和“直播”的人数之比为1∶3,估计参与度在0.4以下的共有多少人?
答案:
一、
1-7 BDDDB CD
二、
8. 频率 概率
9. 相同 越多
10. 5000
11. 0.07
12. 2.4
13. 560
14. 10
三、
15. (1) 0.6
(2) 0.6
(3) 解:黑球个数为40×0.4=16(个),白球40×0.6=24(个).
16. 解:(1) 向上点数为3的频率为;向上点数为5的频率为=;
(2) 小强的说法错误,因为频率最大并不能说明概率最大,只有试验的次数很大时,该事件发生的频率稳定在相应的概率附近;小刚的说法错误,因为事件发生具有随机性,次数不一定是100次.
17. 解:(1)“直播”教学方式学生的参与度更高.理由如下:∵直播参与度为“0.6~0.8”“0.8~1”的人数均大于录播参与度的人数,故“直播”教学方式学生的参与度更高;
(2)P(参与度在0.8及以上)=×100%=30%;
(3)该校共有800名学生,选择“录播”的人数为800×=200(人),选择“直播”的人数为800×=600(人),故参与度在0.4以下的共有200×+600×=20+30=50(人).
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
