2021-2022学年北师大版九年级数学下册3.3垂径定理辅导训练(word解析版)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.3垂径定理辅导训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 435.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 10:58:48 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3.3垂径定理》优生辅导训练(附答案)
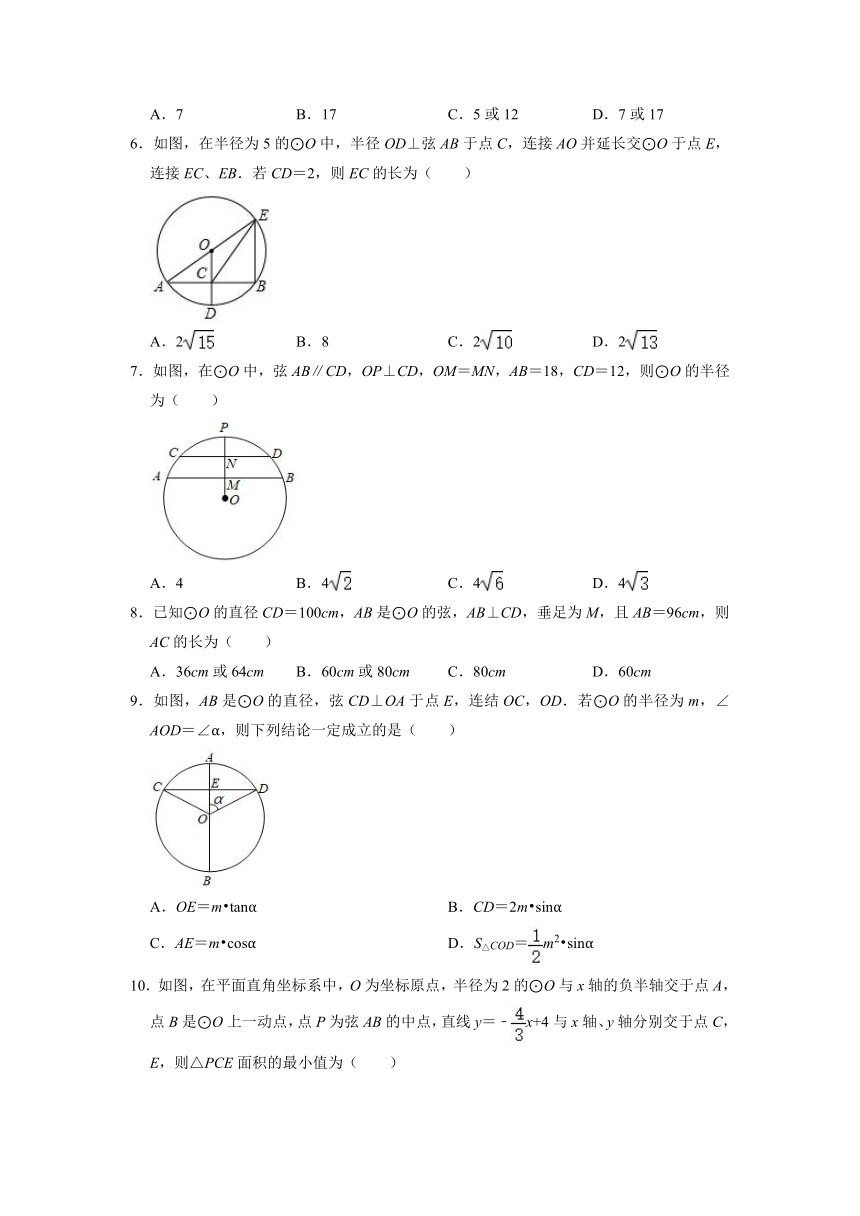
1.已知⊙O的半径为2,点P为⊙O内一定点,且PO=1.过点P作⊙O的弦,其中最短的弦的长度是( )
A.4 B. C.2 D.2
2.如图⊙O的直径CD垂直于弦AB,垂足为P,且AB=6cm,PD=3cm,则⊙O的半径为( )
A.6cm B.5cm C.3cm D.4cm
3.如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )
A.9.6 B.4 C.5 D.10
4.如图,BC为⊙O的直径,弦AD⊥BC于点E,直线l切⊙O于点C,延长OD交l于点F,若AE=2,∠ABC=22.5°,则CF的长度为( )
A.2 B.2 C.2 D.4
5.若弦AB,CD是⊙O的两条平行弦,⊙O的半径为13,AB=10,CD=24,则AB,CD之间的距离为( )
A.7 B.17 C.5或12 D.7或17
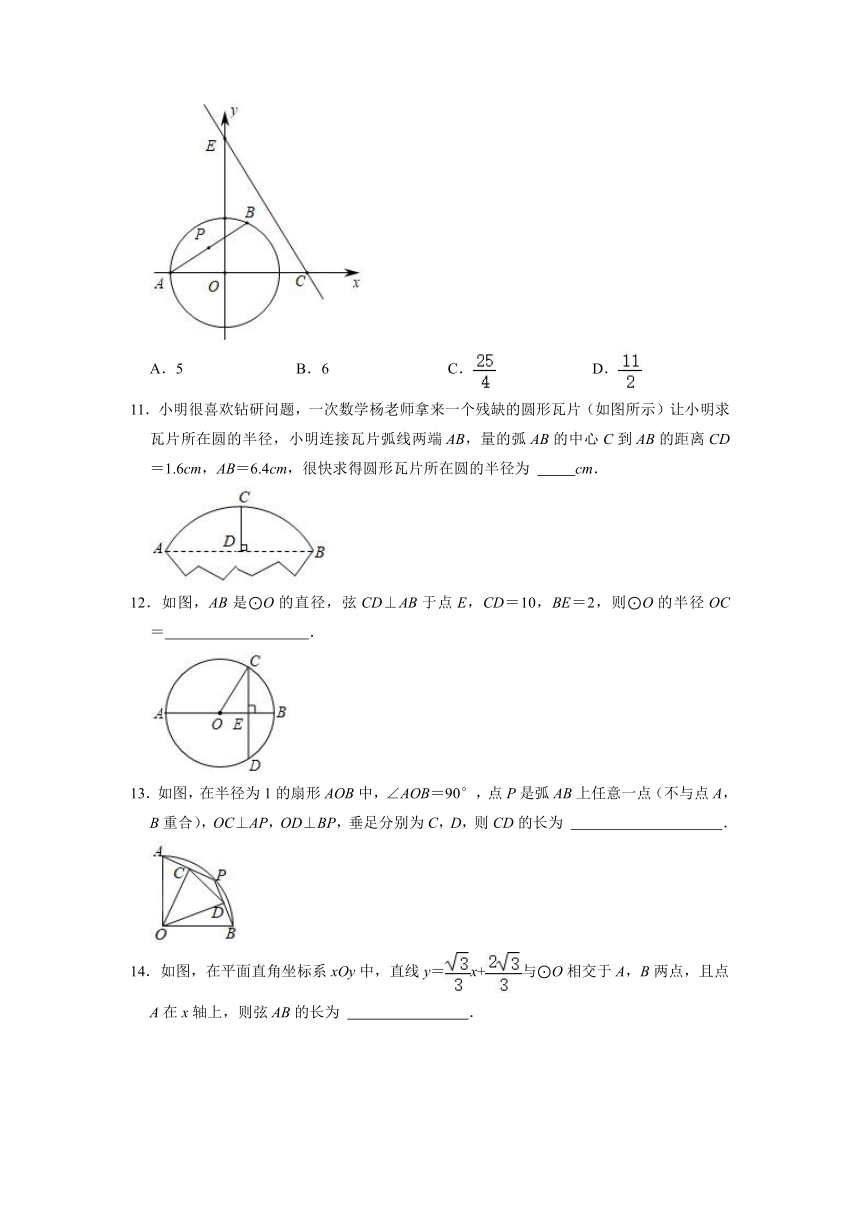
6.如图,在半径为5的⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC、EB.若CD=2,则EC的长为( )
A.2 B.8 C.2 D.2
7.如图,在⊙O中,弦AB∥CD,OP⊥CD,OM=MN,AB=18,CD=12,则⊙O的半径为( )
A.4 B.4 C.4 D.4
8.已知⊙O的直径CD=100cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=96cm,则AC的长为( )
A.36cm或64cm B.60cm或80cm C.80cm D.60cm
9.如图,AB是⊙O的直径,弦CD⊥OA于点E,连结OC,OD.若⊙O的半径为m,∠AOD=∠α,则下列结论一定成立的是( )
A.OE=m tanα B.CD=2m sinα
C.AE=m cosα D.S△COD=m2 sinα
10.如图,在平面直角坐标系中,O为坐标原点,半径为2的⊙O与x轴的负半轴交于点A,点B是⊙O上一动点,点P为弦AB的中点,直线y=﹣x+4与x轴、y轴分别交于点C,E,则△PCE面积的最小值为( )
A.5 B.6 C. D.
11.小明很喜欢钻研问题,一次数学杨老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径,小明连接瓦片弧线两端AB,量的弧AB的中心C到AB的距离CD=1.6cm,AB=6.4cm,很快求得圆形瓦片所在圆的半径为 cm.
12.如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=10,BE=2,则⊙O的半径OC= .
13.如图,在半径为1的扇形AOB中,∠AOB=90°,点P是弧AB上任意一点(不与点A,B重合),OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为 .
14.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
15.一条排水管的截面如图所示,已知排水管的半径OA=2m,水面宽AB=2.4m,某天下雨后,水管水面上升了0.4m,则此时排水管水面宽CD等于 m.
16.在平面直角坐标系xOy中,⊙O的半径为13,直线y=kx﹣3k+4与⊙O交于B,C两点,则弦BC长的最小值等于 .
17.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
18.如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=5,AC=3,CD平行于AB,与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若tan∠C=,求弦MN的长.
19.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
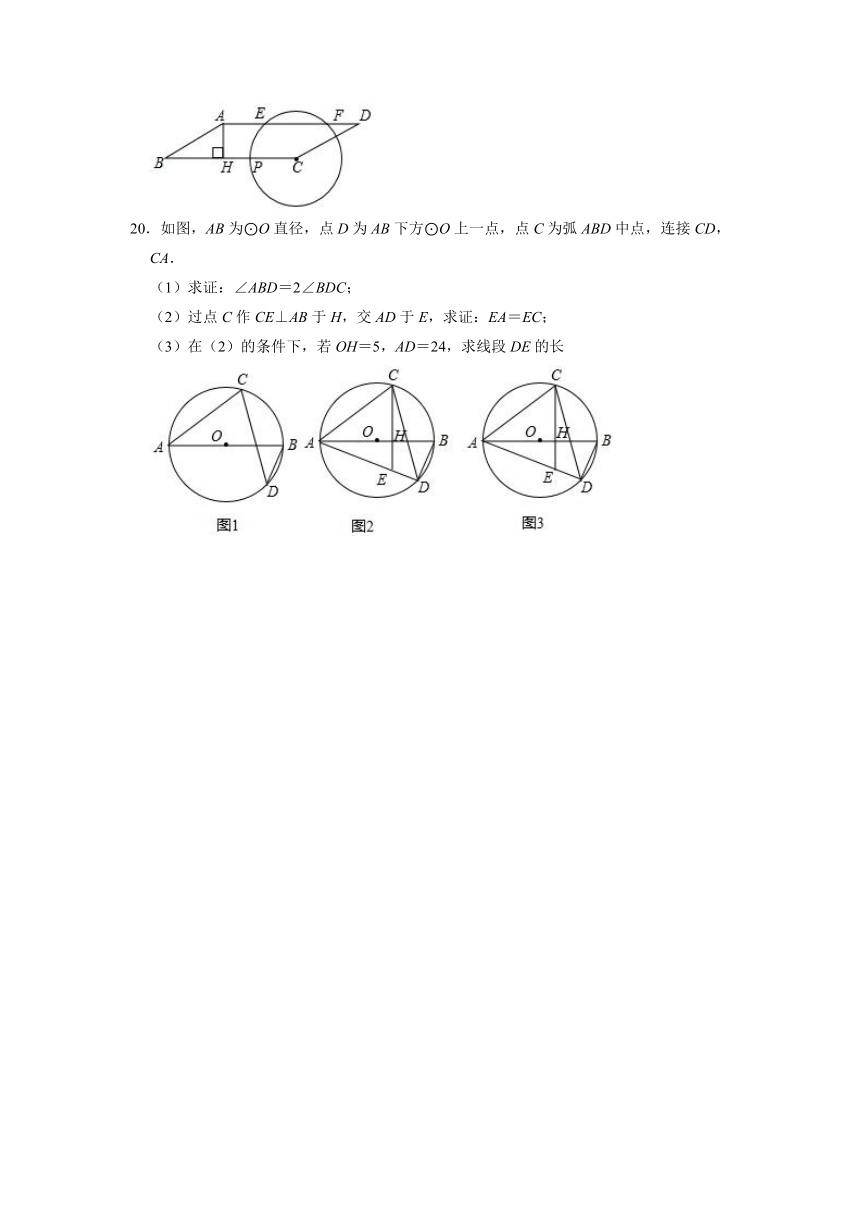
20.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
参考答案
1.解:当过P的弦与OP垂直时,此时的弦长最短,连接OA,
利用垂径定理得到P为AB的中点,即AP=AB,
在Rt△AOP中,OA=2,OP=1,
根据勾股定理得:AP===,
则过点P最短的弦长AB=2.
故选:C.
2.解:连接OA,如图,设⊙O的半径为r cm,则OP=(r﹣3)cm,OA=rcm,
∵CD⊥AB,
∴AP=BP=AB=3cm,
在Rt△OAP中,(r﹣3)2+(3)2=r2,
解得r=6,
即⊙O的半径为6cm.
故选:A.
3.解:∵OE⊥AC于点E.
∴AE=EC.
∵OE=3,OB=5.
∴AE=.
∴AC=8.
∵∠A=∠A,∠AEO=∠AFC.
∴△AEO∽△AFC.
∴,即:.
∴.
∵CD⊥AB.
∴CD=2CF==9.6.
故选:A.
4.解:∵BC为⊙O的直径,弦AD⊥BC于点E,
∴=,AE=DE=2,
∴∠COD=2∠ABC=45°,
∴△OED是等腰直角三角形,
∴OE=ED=2,
∴OD==2,
∵直线l切⊙O于点C,
∴BC⊥CF,
∴△OCF是等腰直角三角形,
∴CF=OC,
∵OC=OD=2,
∴CF=2,
故选:B.
5.解:过O点作OE⊥AB于E,交CD于F,连接OA、OC,如图,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=AB=5,CF=DF=CD=12,
在Rt△OAE中,OE===12,
在Rt△OCF中,OF===5,
当圆心O在AB、CD之间,如图1,EF=OE+OF=12+5=17,
当圆心O不在AB、CD之间,如图2,EF=OE﹣OF=12﹣5=7,
综上所述,AB,CD之间的距离为7或17.
故选:D.
6.解:∵⊙O的半径为5,
∴OA=OD=5,
∵CD=2,
∴OC=OD﹣CD=3,
∵OD⊥AB,
∴AC=BC===4,
∵OA=OE,
∴OC是△ABE的中位线,
∴BE=2OC=6,
∴EC===2,
故选:D.
7.解:如图,连接OA,OC.
∵OP⊥CD,CD∥AB,
∴OP⊥AB,
∴CN=DN=6,AM=MB=9,
设OA=OC=r,OM=MN=a,
则有,
解得,r=4,
故选:C.
8.解:连接AC,AO,
∵⊙O的直径CD=100cm,AB⊥CD,AB=96cm,
∴AM=AB=×96=48(cm),OD=OC=50(cm),
如图1,∵OA=50cm,AM=48cm,CD⊥AB,
∴OM===14(cm),
∴CM=OC+OM=50+14=64(cm),
∴AC===80(cm);
如图2,同理可得,OM=14cm,
∵OC=50cm,
∴MC=50﹣14=36(cm),
在Rt△AMC中,AC==60(cm);
综上所述,AC的长为80cm或60cm,
故选:B.
9.解:∵AB是⊙O的直径,弦CD⊥OA于点E,∴DE=CD,
在Rt△EDO中,OD=m,∠AOD=∠α,
∴tanα=,
∴OE==,
故选项A不符合题意;
∵AB是⊙O的直径,CD⊥OA,
∴CD=2DE,
∵⊙O的半径为m,∠AOD=∠α,
∴DE=OD sinα=m sinα,
∴CD=2DE=2m sinα,
故选项B正确,符合题意;
∵cosα=,
∴OE=OD cosα=m cosα,
∵AO=DO=m,
∴AE=AO﹣OE=m﹣m cosα,
故选项C不符合题意;
∵CD=2m sinα,OE=m cosα,
∴S△COD=CD×OE=×2m sinα×m cosα=m2sinα cosα,
故选项D不符合题意;
故选:B.
10.解:连接OP,如图,
∵点P为弦AB的中点,
∴OP⊥AB,
∴∠APO=90°,
∴P点在以OA为直径的⊙D上(A点除外),
过D点作DH⊥CE于H,DH交⊙D于P′,如图,
∴点P点在P′点的位置时,P点到CE的距离最小,此时△PCE面积有最小值,
当x=0时,y=﹣x+4=4,则E(0,4),
当y=0时,﹣x+4=0,解得x=3,则C(3,0),
∴CE==5,
∵∠DCH=∠ECO,∠CHD=∠COE,
∴△CDH∽△CEO,
∴=,即=,解得DH=,
∴P′H=DH﹣DP′=﹣1=,
∴S△EP′C=×5×=,
∴△PCE面积的最小值为.
故选:D.
11.解:∵C点是的中点,CD⊥AB,
∴CD过圆心,AD=BD=AB=×6.4=3.2(cm),
设圆心为O,连接OA,如图,
设⊙O的半径为Rcm,则OD=(R﹣1.6)cm,
在Rt△OAD中,(R﹣1.6)2+3.22=R2,解得R=4(cm),
所以圆形瓦片所在圆的半径为4cm.
故答案为4.
12.解:∵弦CD⊥AB于点E,CD=10,
∴CE=CD=5,∠OEC=90°,
设OB=OC=x,则OE=x﹣2,
在Rt△OCE中,由勾股定理得:CE2+OE2=OC2,
即52+(x﹣2)2=x2,
解得:x=,
即OC=,
故答案为:.
13.解:连接AB,如图,
∵OA=OB=1,∠AOB=90°,
∴AB=OA=,
∵OC⊥AP,OD⊥BP,
∴AC=PC,BD=PD,
∴CD为△PAB的中位线,
∴CD=AB=.
故答案为.
14.解:设直线AB交y轴于C,过O作OD⊥AB于D,如图:
在y=x+中,令x=0得y=,
∴C(0,),OC=,
在y=x+中令y=0得x+=0,
解得x=﹣2,
∴A(﹣2,0),OA=2,
Rt△AOC中,tan∠CAO===,
∴∠CAO=30°,
Rt△AOD中,AD=OA cos30°=2×=,
∵OD⊥AB,
∴AD=BD=,
∴AB=2,
故答案为:2.
15.解:过O作OE⊥AB于E,交CD于F,连接OC,如图所示:
则AE=BE=AB=1.2(m),OF⊥CD,
∴CF=DF=CD,
∴OE===1.6(m),
∵水管水面上升了0.4m,
∴OF=OE﹣EF=1.6﹣0.4=1.2(m),
∴CF===1.6(m),
∴CD=2CF=3.2(m)
故答案为:3.2.
16.解:∵y=kx﹣3k+4,
∴(x﹣3)k=y﹣4,
∵k为无数个值,
∴x﹣3=0,y﹣4=0,解得x=3,y=4,
∴直线y=kx﹣3k+4过定点(3,4),
如图,P(3,4),连接OB,如图,
当BC⊥OP时,弦BC最短,此时BP=PC,
∵OP==5,
∴BP==12,
∴BC=2BP=24,
即弦BC长的最小值等于24.
故答案为24.
17.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
18.解:(1)∵OA=OB,
∴∠OAB=∠OBA,
∵AB∥CD,
∴∠C=∠OAB,∠D=∠OBA,
∴∠C=∠D,
∴OD=OC=OA+AC=5+3=8;
(2)过O点作OE⊥MN于E,连接OM,如图,则ME=NE,
在Rt△OCE中,tanC==,
设OE=3x,则CE=4x,
∴OC=5x,
即5x=8,解得x=,
∴OE=,
在Rt△OME中,ME===,
∴MN=2ME=.
19.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
20.解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴=,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴△OCH∽△ABD,
∴,
∵OH=5,
∴BD=10,
∴AB==26,
∴AO=13,
∴AH=18,
∵△AHE∽△ADB,
∴,即=,
∴AE=,
∴DE=.
1.已知⊙O的半径为2,点P为⊙O内一定点,且PO=1.过点P作⊙O的弦,其中最短的弦的长度是( )
A.4 B. C.2 D.2
2.如图⊙O的直径CD垂直于弦AB,垂足为P,且AB=6cm,PD=3cm,则⊙O的半径为( )
A.6cm B.5cm C.3cm D.4cm
3.如图,AB为⊙O的直径,弦CD⊥AB于点F,OE⊥AC于点E,若OE=3,OB=5,则CD的长度是( )
A.9.6 B.4 C.5 D.10
4.如图,BC为⊙O的直径,弦AD⊥BC于点E,直线l切⊙O于点C,延长OD交l于点F,若AE=2,∠ABC=22.5°,则CF的长度为( )
A.2 B.2 C.2 D.4
5.若弦AB,CD是⊙O的两条平行弦,⊙O的半径为13,AB=10,CD=24,则AB,CD之间的距离为( )
A.7 B.17 C.5或12 D.7或17
6.如图,在半径为5的⊙O中,半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,连接EC、EB.若CD=2,则EC的长为( )
A.2 B.8 C.2 D.2
7.如图,在⊙O中,弦AB∥CD,OP⊥CD,OM=MN,AB=18,CD=12,则⊙O的半径为( )
A.4 B.4 C.4 D.4
8.已知⊙O的直径CD=100cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=96cm,则AC的长为( )
A.36cm或64cm B.60cm或80cm C.80cm D.60cm
9.如图,AB是⊙O的直径,弦CD⊥OA于点E,连结OC,OD.若⊙O的半径为m,∠AOD=∠α,则下列结论一定成立的是( )
A.OE=m tanα B.CD=2m sinα
C.AE=m cosα D.S△COD=m2 sinα
10.如图,在平面直角坐标系中,O为坐标原点,半径为2的⊙O与x轴的负半轴交于点A,点B是⊙O上一动点,点P为弦AB的中点,直线y=﹣x+4与x轴、y轴分别交于点C,E,则△PCE面积的最小值为( )
A.5 B.6 C. D.
11.小明很喜欢钻研问题,一次数学杨老师拿来一个残缺的圆形瓦片(如图所示)让小明求瓦片所在圆的半径,小明连接瓦片弧线两端AB,量的弧AB的中心C到AB的距离CD=1.6cm,AB=6.4cm,很快求得圆形瓦片所在圆的半径为 cm.
12.如图,AB是⊙O的直径,弦CD⊥AB于点E,CD=10,BE=2,则⊙O的半径OC= .
13.如图,在半径为1的扇形AOB中,∠AOB=90°,点P是弧AB上任意一点(不与点A,B重合),OC⊥AP,OD⊥BP,垂足分别为C,D,则CD的长为 .
14.如图,在平面直角坐标系xOy中,直线y=x+与⊙O相交于A,B两点,且点A在x轴上,则弦AB的长为 .
15.一条排水管的截面如图所示,已知排水管的半径OA=2m,水面宽AB=2.4m,某天下雨后,水管水面上升了0.4m,则此时排水管水面宽CD等于 m.
16.在平面直角坐标系xOy中,⊙O的半径为13,直线y=kx﹣3k+4与⊙O交于B,C两点,则弦BC长的最小值等于 .
17.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
18.如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=5,AC=3,CD平行于AB,与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若tan∠C=,求弦MN的长.
19.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
20.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
参考答案
1.解:当过P的弦与OP垂直时,此时的弦长最短,连接OA,
利用垂径定理得到P为AB的中点,即AP=AB,
在Rt△AOP中,OA=2,OP=1,
根据勾股定理得:AP===,
则过点P最短的弦长AB=2.
故选:C.
2.解:连接OA,如图,设⊙O的半径为r cm,则OP=(r﹣3)cm,OA=rcm,
∵CD⊥AB,
∴AP=BP=AB=3cm,
在Rt△OAP中,(r﹣3)2+(3)2=r2,
解得r=6,
即⊙O的半径为6cm.
故选:A.
3.解:∵OE⊥AC于点E.
∴AE=EC.
∵OE=3,OB=5.
∴AE=.
∴AC=8.
∵∠A=∠A,∠AEO=∠AFC.
∴△AEO∽△AFC.
∴,即:.
∴.
∵CD⊥AB.
∴CD=2CF==9.6.
故选:A.
4.解:∵BC为⊙O的直径,弦AD⊥BC于点E,
∴=,AE=DE=2,
∴∠COD=2∠ABC=45°,
∴△OED是等腰直角三角形,
∴OE=ED=2,
∴OD==2,
∵直线l切⊙O于点C,
∴BC⊥CF,
∴△OCF是等腰直角三角形,
∴CF=OC,
∵OC=OD=2,
∴CF=2,
故选:B.
5.解:过O点作OE⊥AB于E,交CD于F,连接OA、OC,如图,
∵AB∥CD,
∴OF⊥CD,
∴AE=BE=AB=5,CF=DF=CD=12,
在Rt△OAE中,OE===12,
在Rt△OCF中,OF===5,
当圆心O在AB、CD之间,如图1,EF=OE+OF=12+5=17,
当圆心O不在AB、CD之间,如图2,EF=OE﹣OF=12﹣5=7,
综上所述,AB,CD之间的距离为7或17.
故选:D.
6.解:∵⊙O的半径为5,
∴OA=OD=5,
∵CD=2,
∴OC=OD﹣CD=3,
∵OD⊥AB,
∴AC=BC===4,
∵OA=OE,
∴OC是△ABE的中位线,
∴BE=2OC=6,
∴EC===2,
故选:D.
7.解:如图,连接OA,OC.
∵OP⊥CD,CD∥AB,
∴OP⊥AB,
∴CN=DN=6,AM=MB=9,
设OA=OC=r,OM=MN=a,
则有,
解得,r=4,
故选:C.
8.解:连接AC,AO,
∵⊙O的直径CD=100cm,AB⊥CD,AB=96cm,
∴AM=AB=×96=48(cm),OD=OC=50(cm),
如图1,∵OA=50cm,AM=48cm,CD⊥AB,
∴OM===14(cm),
∴CM=OC+OM=50+14=64(cm),
∴AC===80(cm);
如图2,同理可得,OM=14cm,
∵OC=50cm,
∴MC=50﹣14=36(cm),
在Rt△AMC中,AC==60(cm);
综上所述,AC的长为80cm或60cm,
故选:B.
9.解:∵AB是⊙O的直径,弦CD⊥OA于点E,∴DE=CD,
在Rt△EDO中,OD=m,∠AOD=∠α,
∴tanα=,
∴OE==,
故选项A不符合题意;
∵AB是⊙O的直径,CD⊥OA,
∴CD=2DE,
∵⊙O的半径为m,∠AOD=∠α,
∴DE=OD sinα=m sinα,
∴CD=2DE=2m sinα,
故选项B正确,符合题意;
∵cosα=,
∴OE=OD cosα=m cosα,
∵AO=DO=m,
∴AE=AO﹣OE=m﹣m cosα,
故选项C不符合题意;
∵CD=2m sinα,OE=m cosα,
∴S△COD=CD×OE=×2m sinα×m cosα=m2sinα cosα,
故选项D不符合题意;
故选:B.
10.解:连接OP,如图,
∵点P为弦AB的中点,
∴OP⊥AB,
∴∠APO=90°,
∴P点在以OA为直径的⊙D上(A点除外),
过D点作DH⊥CE于H,DH交⊙D于P′,如图,
∴点P点在P′点的位置时,P点到CE的距离最小,此时△PCE面积有最小值,
当x=0时,y=﹣x+4=4,则E(0,4),
当y=0时,﹣x+4=0,解得x=3,则C(3,0),
∴CE==5,
∵∠DCH=∠ECO,∠CHD=∠COE,
∴△CDH∽△CEO,
∴=,即=,解得DH=,
∴P′H=DH﹣DP′=﹣1=,
∴S△EP′C=×5×=,
∴△PCE面积的最小值为.
故选:D.
11.解:∵C点是的中点,CD⊥AB,
∴CD过圆心,AD=BD=AB=×6.4=3.2(cm),
设圆心为O,连接OA,如图,
设⊙O的半径为Rcm,则OD=(R﹣1.6)cm,
在Rt△OAD中,(R﹣1.6)2+3.22=R2,解得R=4(cm),
所以圆形瓦片所在圆的半径为4cm.
故答案为4.
12.解:∵弦CD⊥AB于点E,CD=10,
∴CE=CD=5,∠OEC=90°,
设OB=OC=x,则OE=x﹣2,
在Rt△OCE中,由勾股定理得:CE2+OE2=OC2,
即52+(x﹣2)2=x2,
解得:x=,
即OC=,
故答案为:.
13.解:连接AB,如图,
∵OA=OB=1,∠AOB=90°,
∴AB=OA=,
∵OC⊥AP,OD⊥BP,
∴AC=PC,BD=PD,
∴CD为△PAB的中位线,
∴CD=AB=.
故答案为.
14.解:设直线AB交y轴于C,过O作OD⊥AB于D,如图:
在y=x+中,令x=0得y=,
∴C(0,),OC=,
在y=x+中令y=0得x+=0,
解得x=﹣2,
∴A(﹣2,0),OA=2,
Rt△AOC中,tan∠CAO===,
∴∠CAO=30°,
Rt△AOD中,AD=OA cos30°=2×=,
∵OD⊥AB,
∴AD=BD=,
∴AB=2,
故答案为:2.
15.解:过O作OE⊥AB于E,交CD于F,连接OC,如图所示:
则AE=BE=AB=1.2(m),OF⊥CD,
∴CF=DF=CD,
∴OE===1.6(m),
∵水管水面上升了0.4m,
∴OF=OE﹣EF=1.6﹣0.4=1.2(m),
∴CF===1.6(m),
∴CD=2CF=3.2(m)
故答案为:3.2.
16.解:∵y=kx﹣3k+4,
∴(x﹣3)k=y﹣4,
∵k为无数个值,
∴x﹣3=0,y﹣4=0,解得x=3,y=4,
∴直线y=kx﹣3k+4过定点(3,4),
如图,P(3,4),连接OB,如图,
当BC⊥OP时,弦BC最短,此时BP=PC,
∵OP==5,
∴BP==12,
∴BC=2BP=24,
即弦BC长的最小值等于24.
故答案为24.
17.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
18.解:(1)∵OA=OB,
∴∠OAB=∠OBA,
∵AB∥CD,
∴∠C=∠OAB,∠D=∠OBA,
∴∠C=∠D,
∴OD=OC=OA+AC=5+3=8;
(2)过O点作OE⊥MN于E,连接OM,如图,则ME=NE,
在Rt△OCE中,tanC==,
设OE=3x,则CE=4x,
∴OC=5x,
即5x=8,解得x=,
∴OE=,
在Rt△OME中,ME===,
∴MN=2ME=.
19.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
20.解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴=,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴△OCH∽△ABD,
∴,
∵OH=5,
∴BD=10,
∴AB==26,
∴AO=13,
∴AH=18,
∵△AHE∽△ADB,
∴,即=,
∴AE=,
∴DE=.
