2021-2022学年北师大版数学九年级下册3.4圆周角和圆心角的关系 解答培优练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册3.4圆周角和圆心角的关系 解答培优练习题 (word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 456.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 11:02:01 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.4圆周角与圆心角的关系》
解答培优练习题(附答案)
1.如图,在△ABC中,AB=AC,以AB为直径的半圆O分别交AC、BC于点D、E.
(1)求证:点E是BC的中点.
(2)若∠BOD=75°,求∠CED的度数.
2.如图,AB为⊙O的直径,点 C、D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连接BC、CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
3.如图,线段AB是⊙O的直径,弦CD平分∠ACB,交AB于点E,AC+BC=8.
(1)设点E到BC的距离为y,BC长为x,求y与x的函数关系式,并求当CE取最大值时x的值;
(2)连接AD、BD,四边形ACBD的面积是否为唯一确定的值?如果是,请求出它的面积;如果不是,请说明理由.
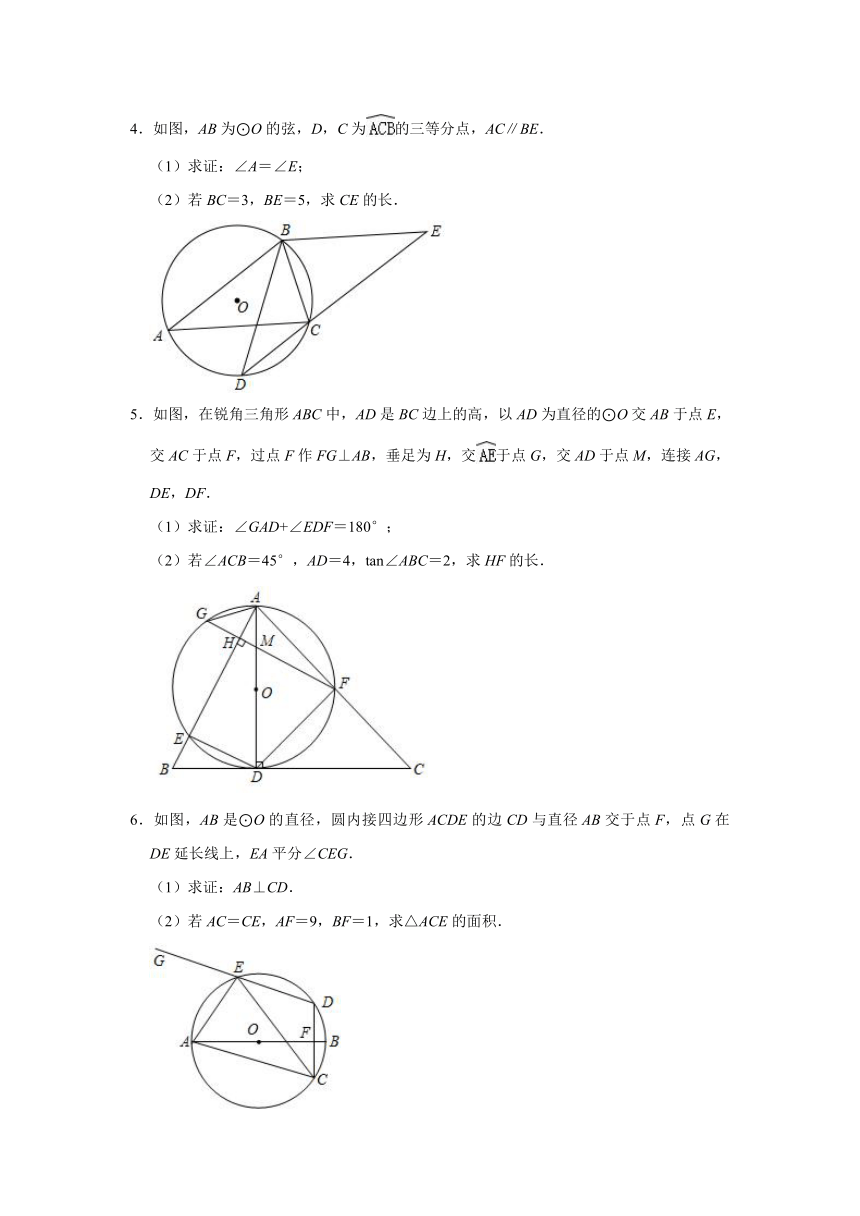
4.如图,AB为⊙O的弦,D,C为的三等分点,AC∥BE.
(1)求证:∠A=∠E;
(2)若BC=3,BE=5,求CE的长.
5.如图,在锐角三角形ABC中,AD是BC边上的高,以AD为直径的⊙O交AB于点E,交AC于点F,过点F作FG⊥AB,垂足为H,交于点G,交AD于点M,连接AG,DE,DF.
(1)求证:∠GAD+∠EDF=180°;
(2)若∠ACB=45°,AD=4,tan∠ABC=2,求HF的长.
6.如图,AB是⊙O的直径,圆内接四边形ACDE的边CD与直径AB交于点F,点G在DE延长线上,EA平分∠CEG.
(1)求证:AB⊥CD.
(2)若AC=CE,AF=9,BF=1,求△ACE的面积.
7.如图,已知AB是⊙O的直径,∠ACD是所对的圆周角,∠ACD=30°.
(1)求∠DAB的度数;
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求DF的长.
8.如图,在锐角三角形ABC中,以AC边为直径的⊙O交BC于点D(BD>CD),作BH⊥AC,依次交⊙O于点E,交AC于点G,交⊙O于H.
(1)求证:△ECD∽△BCE;
(2)若∠ABC=45°,⊙O的直径等于5,BC=7,求CE的长.
9.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC.
(1)求证:AB=AC;
(2)过点D作DE⊥AC,垂足为E.若⊙O的半径为5,∠BAC=60°,求DE的长.
10.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,弦DE∥BC,交AC于点F,弧AD=弧DE,连接AE.
(1)求证:△ADE是等边三角形;
(2)连接OB,若BD=2,求OB的长.
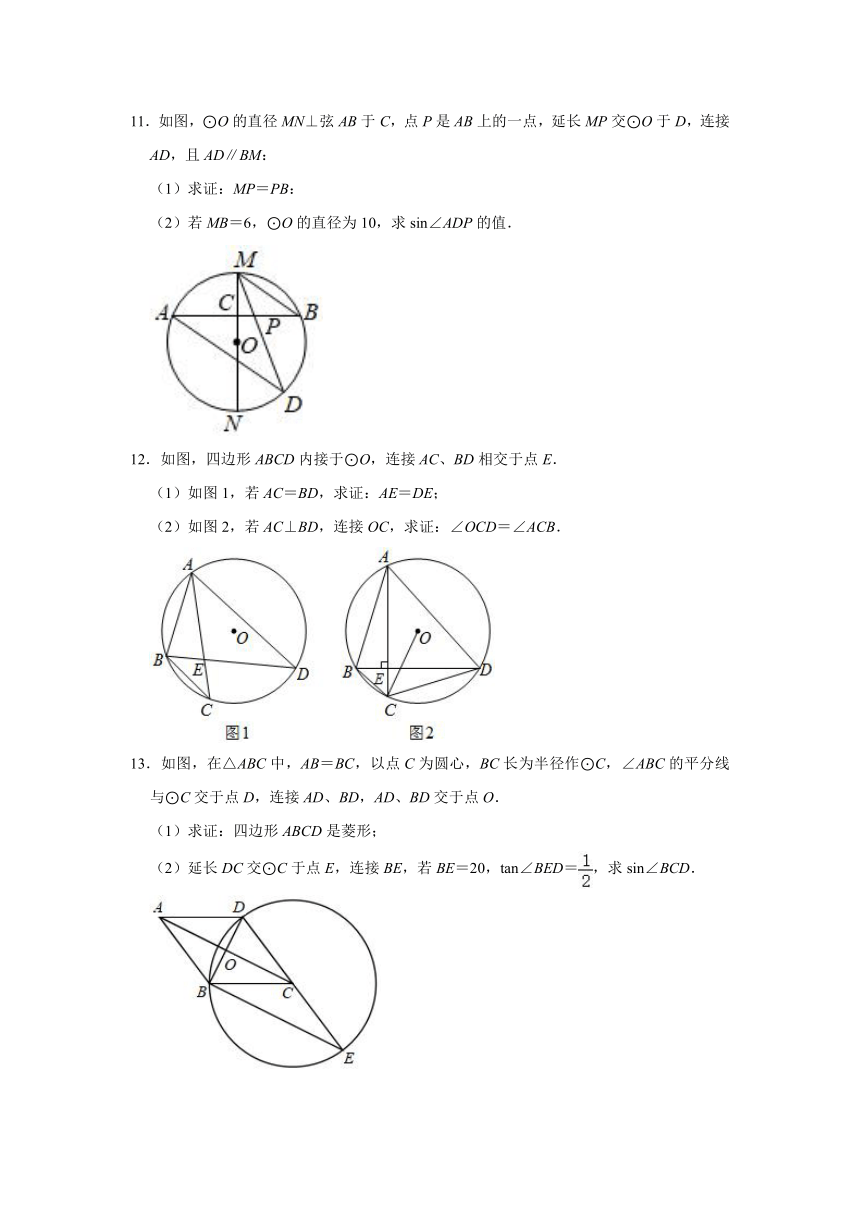
11.如图,⊙O的直径MN⊥弦AB于C,点P是AB上的一点,延长MP交⊙O于D,连接AD,且AD∥BM:
(1)求证:MP=PB:
(2)若MB=6,⊙O的直径为10,求sin∠ADP的值.
12.如图,四边形ABCD内接于⊙O,连接AC、BD相交于点E.
(1)如图1,若AC=BD,求证:AE=DE;
(2)如图2,若AC⊥BD,连接OC,求证:∠OCD=∠ACB.
13.如图,在△ABC中,AB=BC,以点C为圆心,BC长为半径作⊙C,∠ABC的平分线与⊙C交于点D,连接AD、BD,AD、BD交于点O.
(1)求证:四边形ABCD是菱形;
(2)延长DC交⊙C于点E,连接BE,若BE=20,tan∠BED=,求sin∠BCD.
14.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,=.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
15.如图①,在⊙O中,弦CD垂直直径AB于点E.已知AC=4,DB=2.
(1)求直径AB的长.
(2)小慧说“若将题目条件中的‘直径AB′改为‘弦AB’,其余条件均不变(如图②),⊙O的直径仍不变”,你觉得小慧的说法正确吗?请说明理由.
16.已知AB是⊙O的直径,CD是⊙O的弦,连接BD.
(Ⅰ)如图①,连接OC,AD.若∠ADC=56°,求∠CDB及∠COB的大小;
(Ⅱ)如图②,过点C作DB的垂线,交DB的延长线于点E,连接OD.若∠ABD=2∠CDB,∠ODC=20°,求∠DCE的大小.
17.如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,点F为CE的中点,连接DF,DE,AD.
(1)求证:CD=DE.
(2)若OA=5,sin∠CAB=,求DF的长.
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,连接AD,GD,AG.
(1)找出图中和∠ADC相等的角,并给出证明;
(2)已知BE=2,AE=8,求CD的长.
19.如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足H在半径OB上,若劣弧CD沿着直线CD翻折,点B落在OA上的点E处(点E不与点A,O重合),连接CA,CE,CB.
(1)求证:∠ACE=∠DCO.
(2)延长CE交⊙O于点M,连接AM,若AM=10,OE=3,求∠ACE的正弦值.
20.如图,AB是⊙O的直径,点C在⊙O上且不与点A,B重合,∠ABC的平分线交⊙O于点D,过点D作DE⊥AB,垂足为点G,交⊙O于点E,连接CE交BD于点F,连接FG.
(1)求证:FG=DE;
(2)若AB=4,FG=4,求AG的长.
参考答案
1.(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE,
即点E为BC的中点;
(2)解:∵∠BOD=75°,
∴∠DAB=∠BOD=37.5°,
∵∠DAB+∠DEB=180°,∠CED+∠DEB=180°,
∴∠CED=∠DAB=37.5°.
2.证明:(1)在△AOE和△CDE中,
,
∴△AOE≌△CDE(SAS);
(2)∵△AOE≌△CDE,
∴OA=CD,∠AOE=∠D,
∴OB∥CD,
∵OA=OB,
∴OB=CD,
∴四边形OBCD为平行四边形,
∵OB=OD,
∴四边形OBCD是菱形.
3.解:(1)如图1,
过点E作EF⊥BC,垂足为点F,
则点E到BC的距离为EF=y,
∵CD是∠ACB的平分线,且AB为直径,
∴∠ACD=∠BCD=∠ACB=45°,
又EF⊥BC,
∴△CEF是等腰直角三角形,
∴CF=EF=y,
∴BF=BC﹣CF=x﹣y,AC=8﹣BC=8﹣x,
∵∠EBF=∠ABC,∠BFE=∠BCA=90°,
∴△BEF∽△BAC
∴=,即=,
整理,得y=﹣x2+x=﹣(x﹣4)2+2,
∴当x=4时,y有最大值,
在Rt△CEF中,
CE=EF=y,
故当CE取得最大值时,x=4.
(2)如图2,
连接AD、BD,
由(1)可知∠ACD=∠BCD,
∴AD=BD,
又AB为⊙O的直径,
∴∠ADB=90°,
∴△ADB是等腰直角三角形,
∴AD=BD=AB,
∴S△ADB=AD×BD=AB2,
∴AB2=4S△ADB,
∵S△ACB=AC BC,
∴AC BC=2S△ACB,
∵AC+BC=8,
∴(AC+BC)2=64,即AC2+BC2+2AC BC=64,
∵在Rt△ACB中,AC2+BC2=AB2,
∴4S△ADB+4S△ACB=64,
∴S△ADB+S△ACB=16,
∴S四边形ACBD=S△ADB+S△ACB=16.
4.(1)证明:
∵AC∥BE,
∴∠E=∠ACD,
∵D,C为的三等分点,
∴==,
∴∠ACD=∠A,
∴∠E=∠A,
(2)解:由(1)知==,
∴∠D=∠CBD=∠A=∠E,
∴BE=BD=5,BC=CD=3,△CBD∽△BDE,
∴=,即,
解得DE=,
∴CE=DE﹣CD=﹣3=.
5.(1)证明:由题可知∠AGF=∠ADF(同弧所对的圆周角相等),
∵GF⊥AB,AD为圆的直径,
∴∠AGF+∠GAE=90°,∠ADF+∠FAD=90°,
∴∠GAE=∠FAD,
∴∠GAE+∠DAE=∠FAD+∠DAE,即∠GAD=∠EAF,
∵四边形AEDF是圆的内接四边形,
∴∠EAF+∠EDF=180°,
∴∠GAD+∠EDF=180°.
(2)解:如图,
连接OF,
∵AD是圆的直径,且AD是△ABC的高,GF⊥AB,
∴∠AED=∠ADB=∠AHM=∠AFD=90°,
∵∠HAM=∠DAB,
∴△AHM∽△ADB,
∴=,
∵tan∠ABC==2,
∴=2,
∵∠ACB=45°,
∴∠DAC=∠ADF=∠AFO=45°,
∴∠AOF=90°,
∵在Rt△AHM与Rt△FOM中:∠AMH=∠FMO(对顶角),
∴△AHM∽△FOM,
∴==2,
∵AD=4,
∴OF=OA=2,
∴=2,解得OM=1,AM=OA﹣OM=1,
设HM=x,则AH=2x,
在Rt△AHM中有:AH2+HM2=AM2,
即(2x)2+x2=1,解得x1=,x2=﹣(舍去),
∴AH=,
∵OF=OA=2,
∴AF=2,
在Rt△AHF中,有:AH2+HF2=AF2,
即()2+HF2=(2)2,
解得HF=,或HF=﹣(舍去),
故HF的长为.
6.(1)证明:∵AE平分∠CEG,
∴∠AEG=∠AEC,
∵∠AEG+∠AED=180°,∠AED+∠ACD=180°,
∴∠AEG=∠ACD,
∴∠AEC=∠ACD,
∴=,
∴AB⊥CD.
(2)解:如图,连接AD.BD.
∴AB是直径,
∴∠ADB=90°,
∵DF⊥AB,
∴∠AFD=∠DFB=90°,
∵∠ADF+∠DAF=90°,∠ADF+∠FDB=90°,
∴∠DAF=∠FDB,
∴△AFD∽△DFB,
∴DF:FB=AF:DF,
∴DF2=AF BF=9,
∵DF>0,
∴DF=3,
∵AB⊥CD,
∴DF=CF=3,
∴AD=AC,
∴CD=2DF=6,
∵AC=CE,
∴CA=CE=AD,
∴∠CAE=∠CEA=∠ACD=∠ADC,
在△ACE和△DAC中,
,
∴△ACE≌△DAC(AAS),
∴S△ACE=S△ADC= CD AF=×6×9=27.
7.解:(1)如图,连接BD,
∵∠ACD=30°,
∴∠B=∠ACD=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣∠B=60°;
(2)∵∠ADB=90°,∠B=30°,AB=4,
∴AD=AB=2,
∵∠DAB=60°,DE⊥AB,且AB是直径,
∴EF=DE=ADsin60°=,
∴DF=2DE=2.
8.(1)证明:连接AD,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠ADB=90°,
∵BH⊥AC,
∴∠BGC=90°,
∵∠DAC+∠ACD=∠GBC+∠ACD=90°,
∴∠DAC=∠GBC,
又∵∠DAC=∠DEC,
∴∠EBC=∠DEC,
∵∠ECD=∠BCE,
∴△ECD∽△BCE;
(2)解:由(1)得:∠EBC=∠DEC,
∵∠ABG+∠DEC=45°,
∴∠ABC=45°,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴BD=AD,
∴AD+DC=BD+DC=BC=7,
∵∠ADC=90°,AC=5,
∴AD2+DC2=AC2,即(7﹣DC)2+DC2=52,
解得:DC=4或DC=3,
∵∠DAC=∠GBC<45°,
∴AD>DC,
∴DC=3,AD=4,
由(1)得:△ECD∽△BCE,
∴CE:BC=CD:CE,
∴CE2=CD×BC=3×7=21,
∴CE=.
9.解:(1)证明:连接AD,如图,
∵AB是⊙O的直径,
∴∠ADB=90°,又BD=CD
∴AD是BC的垂直平分线,
∴AB=AC,
(2)∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵⊙O的半径为5,
∴AB=BC=10,CD=BC=5,
又∵∠C=60°,
∴DE=CD sin60°=.
10.(1)证明:∵AC是⊙O的直径,DE∥BC,
∴DE⊥AC,
∴EF=DF=DE,
∵弧AD=弧DE,
∴AD=DE,
∴DF=AD,
∵DF=DE,
∴∠DAF=30°,
∴∠ADE=60°,
∵AD=DE,
∴△ADE是等边三角形;
(2)解:连接CD,
∵AC是⊙O的直径,DE∥BC,
∴∠CDB=90°,
由(1)得△ADE是等边三角形,DE⊥AC,∠DAF=30°,
∴∠DCA=60°,CD=AC=OC,
∵∠ACB=90°,
∴∠DCB=30°,
∴BC=2BD=4,
∴CD==2,
∴OC=CD=2,
∴OB==2.
11.(1)证明:∵AD∥BM,
∴∠D=∠BMD,
∵∠D=∠ABM,
∴∠BMD=∠ABM,
∴MP=PB;
(2)解:连接NB,如图,
∵MN为⊙O的直径,
∴∠MBN=90°,
∵MN⊥AB,
∴=,
∴∠BNM=∠ADM,
在Rt△BMN中,sin∠BNM===,
∴sin∠ADP=.
12.证明:(1)∵AC=BD,
∴=,
即+=+,
∴=,
∴∠ADB=∠CAD,
∴AE=DE;
(2)作直径CF,连接DF,如图2,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADE+∠CAD=90°,
∵∠ACB=∠ADE,∠F=∠CAD,
∴∠ACB+∠F=90°,
∵CF为直径,
∴∠CDF=90°,
∴∠F+∠FCD=90°,
∴∠ACB=∠FCD,
即∠OCD=∠ACB.
13.(1)证明:由题意得,BC=CD,
∴AB=BC=CD,
∴∠1=∠CDB,
∵BD是∠ABC的平分线,
∴∠1=∠2,
∴∠2=∠CDB,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形.
(2)解:过点D作DH⊥BC交BC于点H.
由题意得,DE是⊙O的直径,
∴∠DBE=90°,
在Rt△DBE中,BE=20,
∴BD=10,,
∴,
∵四边形ABCD是菱形,
∴,点O是AC的中点,
∵点C是DE的中点,
∴,
∴AC=2OC=20,
∵,
即,
∴,
在Rt△DBE中,∠DHC=90°,
∴.
14.解:(1)∵=,
∴OD⊥AC,
又∵AB是⊙O的直径,
∴∠ACB=90°,即BC⊥AC,
∴:OD∥BC.
(2)∵AD=CD,
∴OD⊥AC于点E且AE=CE,
又∵AC=10,
∴,
∵DE=4,
设⊙O半径为R,则OA=R,OE=R﹣4,
在Rt△AOE中,
OA2=OE2+AE2,即R2=(R﹣4)2+52,
∴,
又∵O,E为AB,AC的中点,
∴OE=,OE∥BC,
∴BC=2OE=.
15.解:(1)连接AD,如图所示:
∵AB为直径,
∴∠ADB=90°,
∵弦CD垂直直径AB于点E,
∴由垂径定理可知:AD=AC=4,
在Rt△ADB中,AB=;
(2)小慧的说法正确;理由如下:连接AO,并延长AO交⊙O于点F,连接CF,如图所示:
∵AF为直径,
∴∠ACF=90°,即∠ACD+∠FCD=90°,
又∵AB⊥CD,
∴∠EBD+∠BDE=90°,
而∠DBE=∠ACD,
∴∠FCD=∠BDE,
∴,
∴,
∴CF=BD=2,
在Rt△ACF中,AF==,
∴⊙O的直径仍不变.
16.解:(Ⅰ)∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ADC=56°,
∴∠CDB=90°﹣∠ADC=90°﹣56°=34°,
在⊙O中,∠COB=2∠CDB=2×34°=68°.
(II )∵OD=OB,
∴∠ODB=∠OBD,
即∠ODC+∠CDB=∠OBD,
∵∠ABD=2∠CDB,∠ODC=20°,
∴20°+∠CDB=2∠CDB,
∴∠CDB=20°,
∵CE⊥DE,
∴∠CED=90°,
在Rt△CDE中,∠DCE=90°﹣∠CDE=90°﹣20°=70°.
17.证明:(1)∵AB=AC,
∴∠C=∠B,
∵圆内接四边形ABDE,
∴∠CED=∠B,
∴∠CED=∠C,
∴CD=DE,
解:(2)连接BE,
∵AB为直径,
∴∠AEB=90°,
∵sin∠CAB=,AB=2OA=10,
∴BE=8,
∵AB=AC,
∴△ABC为等腰三角形,
∵AB为直径,
∴∠ADC=90°
∴AD⊥BC,
由三线合一得:D是BC的中点,
∵点F为CE的中点,
∴FD为△CEB的中位线,
∴DF==4.
18.解:(1)∠AGD=∠ADC,
理由如下:∵弦CD⊥AB,
∴DE=CE,=,
∴∠AGD=∠ADC;
(2)方法一、如图,连接AC,BC,
∵AB是直径,
∴∠ACB=90°,
∴∠ACE+∠BCE=90°=∠ACE+∠CAE,
∴∠BCE=∠CAE,
又∵∠AEC=∠BEC=90°,
∴△ACE∽△CBE,
∴,
∴CE CE=2×8=16,
∴CE=4,
∴CD=8.
方法二、连接OC,
∵BE=2,AE=8,
∴BA=10,
∴OC=OB=5,
∴OE=3,
∴CE===4,
∴CD=8.
19.(1)证明:连接CO,
由翻折可知∠ECH=∠BCH,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠BCH+∠ACH=90°,
∵CD⊥AB,
∴∠CAO+∠ACH=90°,
∴∠BCH=∠CAO=∠ACO,
∴∠ECH=∠ACO,
即∠ACE+∠ECO=∠DCO+∠ECO,
∴∠ACE=∠DCO.
(2)解:连接CO,
由翻折可知∠B=∠CEB,EH=BH,
∵∠B=∠AMC,∠CEB=∠AEM,
∴∠AMC=∠AEM,
∴AE=AM=10,
∴OC=OA=13,
∴3+OH=13﹣OH,
∴OH=5,
∴sin∠ACE=sin∠DCO=.
20.(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠E=∠CBD,
∴∠E=∠ABD,
∵DE⊥AB,
∴DG=EG,∠BGD=90°,
∵∠ABD+∠BDG=90°,
∴∠E+∠FDE=90°,
∴∠EFD=90°,
∴GF=DE;
(2)解:连接OD,如图,则OD=OA=AB=2,
∵FG=DG=4,
∴OG==2,
∴AG=OA﹣OG=2﹣2.
解答培优练习题(附答案)
1.如图,在△ABC中,AB=AC,以AB为直径的半圆O分别交AC、BC于点D、E.
(1)求证:点E是BC的中点.
(2)若∠BOD=75°,求∠CED的度数.
2.如图,AB为⊙O的直径,点 C、D在⊙O上,AC与OD交于点E,AE=EC,OE=ED.连接BC、CD.求证:
(1)△AOE≌△CDE;
(2)四边形OBCD是菱形.
3.如图,线段AB是⊙O的直径,弦CD平分∠ACB,交AB于点E,AC+BC=8.
(1)设点E到BC的距离为y,BC长为x,求y与x的函数关系式,并求当CE取最大值时x的值;
(2)连接AD、BD,四边形ACBD的面积是否为唯一确定的值?如果是,请求出它的面积;如果不是,请说明理由.
4.如图,AB为⊙O的弦,D,C为的三等分点,AC∥BE.
(1)求证:∠A=∠E;
(2)若BC=3,BE=5,求CE的长.
5.如图,在锐角三角形ABC中,AD是BC边上的高,以AD为直径的⊙O交AB于点E,交AC于点F,过点F作FG⊥AB,垂足为H,交于点G,交AD于点M,连接AG,DE,DF.
(1)求证:∠GAD+∠EDF=180°;
(2)若∠ACB=45°,AD=4,tan∠ABC=2,求HF的长.
6.如图,AB是⊙O的直径,圆内接四边形ACDE的边CD与直径AB交于点F,点G在DE延长线上,EA平分∠CEG.
(1)求证:AB⊥CD.
(2)若AC=CE,AF=9,BF=1,求△ACE的面积.
7.如图,已知AB是⊙O的直径,∠ACD是所对的圆周角,∠ACD=30°.
(1)求∠DAB的度数;
(2)过点D作DE⊥AB,垂足为E,DE的延长线交⊙O于点F.若AB=4,求DF的长.
8.如图,在锐角三角形ABC中,以AC边为直径的⊙O交BC于点D(BD>CD),作BH⊥AC,依次交⊙O于点E,交AC于点G,交⊙O于H.
(1)求证:△ECD∽△BCE;
(2)若∠ABC=45°,⊙O的直径等于5,BC=7,求CE的长.
9.如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC.
(1)求证:AB=AC;
(2)过点D作DE⊥AC,垂足为E.若⊙O的半径为5,∠BAC=60°,求DE的长.
10.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,弦DE∥BC,交AC于点F,弧AD=弧DE,连接AE.
(1)求证:△ADE是等边三角形;
(2)连接OB,若BD=2,求OB的长.
11.如图,⊙O的直径MN⊥弦AB于C,点P是AB上的一点,延长MP交⊙O于D,连接AD,且AD∥BM:
(1)求证:MP=PB:
(2)若MB=6,⊙O的直径为10,求sin∠ADP的值.
12.如图,四边形ABCD内接于⊙O,连接AC、BD相交于点E.
(1)如图1,若AC=BD,求证:AE=DE;
(2)如图2,若AC⊥BD,连接OC,求证:∠OCD=∠ACB.
13.如图,在△ABC中,AB=BC,以点C为圆心,BC长为半径作⊙C,∠ABC的平分线与⊙C交于点D,连接AD、BD,AD、BD交于点O.
(1)求证:四边形ABCD是菱形;
(2)延长DC交⊙C于点E,连接BE,若BE=20,tan∠BED=,求sin∠BCD.
14.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,=.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
15.如图①,在⊙O中,弦CD垂直直径AB于点E.已知AC=4,DB=2.
(1)求直径AB的长.
(2)小慧说“若将题目条件中的‘直径AB′改为‘弦AB’,其余条件均不变(如图②),⊙O的直径仍不变”,你觉得小慧的说法正确吗?请说明理由.
16.已知AB是⊙O的直径,CD是⊙O的弦,连接BD.
(Ⅰ)如图①,连接OC,AD.若∠ADC=56°,求∠CDB及∠COB的大小;
(Ⅱ)如图②,过点C作DB的垂线,交DB的延长线于点E,连接OD.若∠ABD=2∠CDB,∠ODC=20°,求∠DCE的大小.
17.如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,点F为CE的中点,连接DF,DE,AD.
(1)求证:CD=DE.
(2)若OA=5,sin∠CAB=,求DF的长.
18.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,连接AD,GD,AG.
(1)找出图中和∠ADC相等的角,并给出证明;
(2)已知BE=2,AE=8,求CD的长.
19.如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,垂足H在半径OB上,若劣弧CD沿着直线CD翻折,点B落在OA上的点E处(点E不与点A,O重合),连接CA,CE,CB.
(1)求证:∠ACE=∠DCO.
(2)延长CE交⊙O于点M,连接AM,若AM=10,OE=3,求∠ACE的正弦值.
20.如图,AB是⊙O的直径,点C在⊙O上且不与点A,B重合,∠ABC的平分线交⊙O于点D,过点D作DE⊥AB,垂足为点G,交⊙O于点E,连接CE交BD于点F,连接FG.
(1)求证:FG=DE;
(2)若AB=4,FG=4,求AG的长.
参考答案
1.(1)证明:连接AE,
∵AB为⊙O的直径,
∴∠AEB=90°,即AE⊥BC,
∵AB=AC,
∴BE=CE,
即点E为BC的中点;
(2)解:∵∠BOD=75°,
∴∠DAB=∠BOD=37.5°,
∵∠DAB+∠DEB=180°,∠CED+∠DEB=180°,
∴∠CED=∠DAB=37.5°.
2.证明:(1)在△AOE和△CDE中,
,
∴△AOE≌△CDE(SAS);
(2)∵△AOE≌△CDE,
∴OA=CD,∠AOE=∠D,
∴OB∥CD,
∵OA=OB,
∴OB=CD,
∴四边形OBCD为平行四边形,
∵OB=OD,
∴四边形OBCD是菱形.
3.解:(1)如图1,
过点E作EF⊥BC,垂足为点F,
则点E到BC的距离为EF=y,
∵CD是∠ACB的平分线,且AB为直径,
∴∠ACD=∠BCD=∠ACB=45°,
又EF⊥BC,
∴△CEF是等腰直角三角形,
∴CF=EF=y,
∴BF=BC﹣CF=x﹣y,AC=8﹣BC=8﹣x,
∵∠EBF=∠ABC,∠BFE=∠BCA=90°,
∴△BEF∽△BAC
∴=,即=,
整理,得y=﹣x2+x=﹣(x﹣4)2+2,
∴当x=4时,y有最大值,
在Rt△CEF中,
CE=EF=y,
故当CE取得最大值时,x=4.
(2)如图2,
连接AD、BD,
由(1)可知∠ACD=∠BCD,
∴AD=BD,
又AB为⊙O的直径,
∴∠ADB=90°,
∴△ADB是等腰直角三角形,
∴AD=BD=AB,
∴S△ADB=AD×BD=AB2,
∴AB2=4S△ADB,
∵S△ACB=AC BC,
∴AC BC=2S△ACB,
∵AC+BC=8,
∴(AC+BC)2=64,即AC2+BC2+2AC BC=64,
∵在Rt△ACB中,AC2+BC2=AB2,
∴4S△ADB+4S△ACB=64,
∴S△ADB+S△ACB=16,
∴S四边形ACBD=S△ADB+S△ACB=16.
4.(1)证明:
∵AC∥BE,
∴∠E=∠ACD,
∵D,C为的三等分点,
∴==,
∴∠ACD=∠A,
∴∠E=∠A,
(2)解:由(1)知==,
∴∠D=∠CBD=∠A=∠E,
∴BE=BD=5,BC=CD=3,△CBD∽△BDE,
∴=,即,
解得DE=,
∴CE=DE﹣CD=﹣3=.
5.(1)证明:由题可知∠AGF=∠ADF(同弧所对的圆周角相等),
∵GF⊥AB,AD为圆的直径,
∴∠AGF+∠GAE=90°,∠ADF+∠FAD=90°,
∴∠GAE=∠FAD,
∴∠GAE+∠DAE=∠FAD+∠DAE,即∠GAD=∠EAF,
∵四边形AEDF是圆的内接四边形,
∴∠EAF+∠EDF=180°,
∴∠GAD+∠EDF=180°.
(2)解:如图,
连接OF,
∵AD是圆的直径,且AD是△ABC的高,GF⊥AB,
∴∠AED=∠ADB=∠AHM=∠AFD=90°,
∵∠HAM=∠DAB,
∴△AHM∽△ADB,
∴=,
∵tan∠ABC==2,
∴=2,
∵∠ACB=45°,
∴∠DAC=∠ADF=∠AFO=45°,
∴∠AOF=90°,
∵在Rt△AHM与Rt△FOM中:∠AMH=∠FMO(对顶角),
∴△AHM∽△FOM,
∴==2,
∵AD=4,
∴OF=OA=2,
∴=2,解得OM=1,AM=OA﹣OM=1,
设HM=x,则AH=2x,
在Rt△AHM中有:AH2+HM2=AM2,
即(2x)2+x2=1,解得x1=,x2=﹣(舍去),
∴AH=,
∵OF=OA=2,
∴AF=2,
在Rt△AHF中,有:AH2+HF2=AF2,
即()2+HF2=(2)2,
解得HF=,或HF=﹣(舍去),
故HF的长为.
6.(1)证明:∵AE平分∠CEG,
∴∠AEG=∠AEC,
∵∠AEG+∠AED=180°,∠AED+∠ACD=180°,
∴∠AEG=∠ACD,
∴∠AEC=∠ACD,
∴=,
∴AB⊥CD.
(2)解:如图,连接AD.BD.
∴AB是直径,
∴∠ADB=90°,
∵DF⊥AB,
∴∠AFD=∠DFB=90°,
∵∠ADF+∠DAF=90°,∠ADF+∠FDB=90°,
∴∠DAF=∠FDB,
∴△AFD∽△DFB,
∴DF:FB=AF:DF,
∴DF2=AF BF=9,
∵DF>0,
∴DF=3,
∵AB⊥CD,
∴DF=CF=3,
∴AD=AC,
∴CD=2DF=6,
∵AC=CE,
∴CA=CE=AD,
∴∠CAE=∠CEA=∠ACD=∠ADC,
在△ACE和△DAC中,
,
∴△ACE≌△DAC(AAS),
∴S△ACE=S△ADC= CD AF=×6×9=27.
7.解:(1)如图,连接BD,
∵∠ACD=30°,
∴∠B=∠ACD=30°,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB=90°﹣∠B=60°;
(2)∵∠ADB=90°,∠B=30°,AB=4,
∴AD=AB=2,
∵∠DAB=60°,DE⊥AB,且AB是直径,
∴EF=DE=ADsin60°=,
∴DF=2DE=2.
8.(1)证明:连接AD,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠ADB=90°,
∵BH⊥AC,
∴∠BGC=90°,
∵∠DAC+∠ACD=∠GBC+∠ACD=90°,
∴∠DAC=∠GBC,
又∵∠DAC=∠DEC,
∴∠EBC=∠DEC,
∵∠ECD=∠BCE,
∴△ECD∽△BCE;
(2)解:由(1)得:∠EBC=∠DEC,
∵∠ABG+∠DEC=45°,
∴∠ABC=45°,∠BAD=45°,
∴△ABD是等腰直角三角形,
∴BD=AD,
∴AD+DC=BD+DC=BC=7,
∵∠ADC=90°,AC=5,
∴AD2+DC2=AC2,即(7﹣DC)2+DC2=52,
解得:DC=4或DC=3,
∵∠DAC=∠GBC<45°,
∴AD>DC,
∴DC=3,AD=4,
由(1)得:△ECD∽△BCE,
∴CE:BC=CD:CE,
∴CE2=CD×BC=3×7=21,
∴CE=.
9.解:(1)证明:连接AD,如图,
∵AB是⊙O的直径,
∴∠ADB=90°,又BD=CD
∴AD是BC的垂直平分线,
∴AB=AC,
(2)∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∵⊙O的半径为5,
∴AB=BC=10,CD=BC=5,
又∵∠C=60°,
∴DE=CD sin60°=.
10.(1)证明:∵AC是⊙O的直径,DE∥BC,
∴DE⊥AC,
∴EF=DF=DE,
∵弧AD=弧DE,
∴AD=DE,
∴DF=AD,
∵DF=DE,
∴∠DAF=30°,
∴∠ADE=60°,
∵AD=DE,
∴△ADE是等边三角形;
(2)解:连接CD,
∵AC是⊙O的直径,DE∥BC,
∴∠CDB=90°,
由(1)得△ADE是等边三角形,DE⊥AC,∠DAF=30°,
∴∠DCA=60°,CD=AC=OC,
∵∠ACB=90°,
∴∠DCB=30°,
∴BC=2BD=4,
∴CD==2,
∴OC=CD=2,
∴OB==2.
11.(1)证明:∵AD∥BM,
∴∠D=∠BMD,
∵∠D=∠ABM,
∴∠BMD=∠ABM,
∴MP=PB;
(2)解:连接NB,如图,
∵MN为⊙O的直径,
∴∠MBN=90°,
∵MN⊥AB,
∴=,
∴∠BNM=∠ADM,
在Rt△BMN中,sin∠BNM===,
∴sin∠ADP=.
12.证明:(1)∵AC=BD,
∴=,
即+=+,
∴=,
∴∠ADB=∠CAD,
∴AE=DE;
(2)作直径CF,连接DF,如图2,
∵AC⊥BD,
∴∠AED=90°,
∴∠ADE+∠CAD=90°,
∵∠ACB=∠ADE,∠F=∠CAD,
∴∠ACB+∠F=90°,
∵CF为直径,
∴∠CDF=90°,
∴∠F+∠FCD=90°,
∴∠ACB=∠FCD,
即∠OCD=∠ACB.
13.(1)证明:由题意得,BC=CD,
∴AB=BC=CD,
∴∠1=∠CDB,
∵BD是∠ABC的平分线,
∴∠1=∠2,
∴∠2=∠CDB,
∴AB∥CD,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形.
(2)解:过点D作DH⊥BC交BC于点H.
由题意得,DE是⊙O的直径,
∴∠DBE=90°,
在Rt△DBE中,BE=20,
∴BD=10,,
∴,
∵四边形ABCD是菱形,
∴,点O是AC的中点,
∵点C是DE的中点,
∴,
∴AC=2OC=20,
∵,
即,
∴,
在Rt△DBE中,∠DHC=90°,
∴.
14.解:(1)∵=,
∴OD⊥AC,
又∵AB是⊙O的直径,
∴∠ACB=90°,即BC⊥AC,
∴:OD∥BC.
(2)∵AD=CD,
∴OD⊥AC于点E且AE=CE,
又∵AC=10,
∴,
∵DE=4,
设⊙O半径为R,则OA=R,OE=R﹣4,
在Rt△AOE中,
OA2=OE2+AE2,即R2=(R﹣4)2+52,
∴,
又∵O,E为AB,AC的中点,
∴OE=,OE∥BC,
∴BC=2OE=.
15.解:(1)连接AD,如图所示:
∵AB为直径,
∴∠ADB=90°,
∵弦CD垂直直径AB于点E,
∴由垂径定理可知:AD=AC=4,
在Rt△ADB中,AB=;
(2)小慧的说法正确;理由如下:连接AO,并延长AO交⊙O于点F,连接CF,如图所示:
∵AF为直径,
∴∠ACF=90°,即∠ACD+∠FCD=90°,
又∵AB⊥CD,
∴∠EBD+∠BDE=90°,
而∠DBE=∠ACD,
∴∠FCD=∠BDE,
∴,
∴,
∴CF=BD=2,
在Rt△ACF中,AF==,
∴⊙O的直径仍不变.
16.解:(Ⅰ)∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ADC=56°,
∴∠CDB=90°﹣∠ADC=90°﹣56°=34°,
在⊙O中,∠COB=2∠CDB=2×34°=68°.
(II )∵OD=OB,
∴∠ODB=∠OBD,
即∠ODC+∠CDB=∠OBD,
∵∠ABD=2∠CDB,∠ODC=20°,
∴20°+∠CDB=2∠CDB,
∴∠CDB=20°,
∵CE⊥DE,
∴∠CED=90°,
在Rt△CDE中,∠DCE=90°﹣∠CDE=90°﹣20°=70°.
17.证明:(1)∵AB=AC,
∴∠C=∠B,
∵圆内接四边形ABDE,
∴∠CED=∠B,
∴∠CED=∠C,
∴CD=DE,
解:(2)连接BE,
∵AB为直径,
∴∠AEB=90°,
∵sin∠CAB=,AB=2OA=10,
∴BE=8,
∵AB=AC,
∴△ABC为等腰三角形,
∵AB为直径,
∴∠ADC=90°
∴AD⊥BC,
由三线合一得:D是BC的中点,
∵点F为CE的中点,
∴FD为△CEB的中位线,
∴DF==4.
18.解:(1)∠AGD=∠ADC,
理由如下:∵弦CD⊥AB,
∴DE=CE,=,
∴∠AGD=∠ADC;
(2)方法一、如图,连接AC,BC,
∵AB是直径,
∴∠ACB=90°,
∴∠ACE+∠BCE=90°=∠ACE+∠CAE,
∴∠BCE=∠CAE,
又∵∠AEC=∠BEC=90°,
∴△ACE∽△CBE,
∴,
∴CE CE=2×8=16,
∴CE=4,
∴CD=8.
方法二、连接OC,
∵BE=2,AE=8,
∴BA=10,
∴OC=OB=5,
∴OE=3,
∴CE===4,
∴CD=8.
19.(1)证明:连接CO,
由翻折可知∠ECH=∠BCH,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴∠BCH+∠ACH=90°,
∵CD⊥AB,
∴∠CAO+∠ACH=90°,
∴∠BCH=∠CAO=∠ACO,
∴∠ECH=∠ACO,
即∠ACE+∠ECO=∠DCO+∠ECO,
∴∠ACE=∠DCO.
(2)解:连接CO,
由翻折可知∠B=∠CEB,EH=BH,
∵∠B=∠AMC,∠CEB=∠AEM,
∴∠AMC=∠AEM,
∴AE=AM=10,
∴OC=OA=13,
∴3+OH=13﹣OH,
∴OH=5,
∴sin∠ACE=sin∠DCO=.
20.(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD,
∵∠E=∠CBD,
∴∠E=∠ABD,
∵DE⊥AB,
∴DG=EG,∠BGD=90°,
∵∠ABD+∠BDG=90°,
∴∠E+∠FDE=90°,
∴∠EFD=90°,
∴GF=DE;
(2)解:连接OD,如图,则OD=OA=AB=2,
∵FG=DG=4,
∴OG==2,
∴AG=OA﹣OG=2﹣2.
