2021-2022学年北师大版九年级数学下册3.4圆周角与圆心角的关系优生辅导训练(word解析版)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.4圆周角与圆心角的关系优生辅导训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 411.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 11:05:50 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学下册《3.4圆周角与圆心角的关系》
优生辅导训练(附答案)
1.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
A.20° B.35° C.40° D.55°
2.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+ B.2+ C.4 D.2+2
3.如图,⊙O中,弦AB与直径CD相交于点P,且PA=4,PB=6,PD=2,则⊙O的半径为( )
A.9 B.8 C.7 D.6
4.如图所示,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是( )
A.6 B.5 C.4 D.3
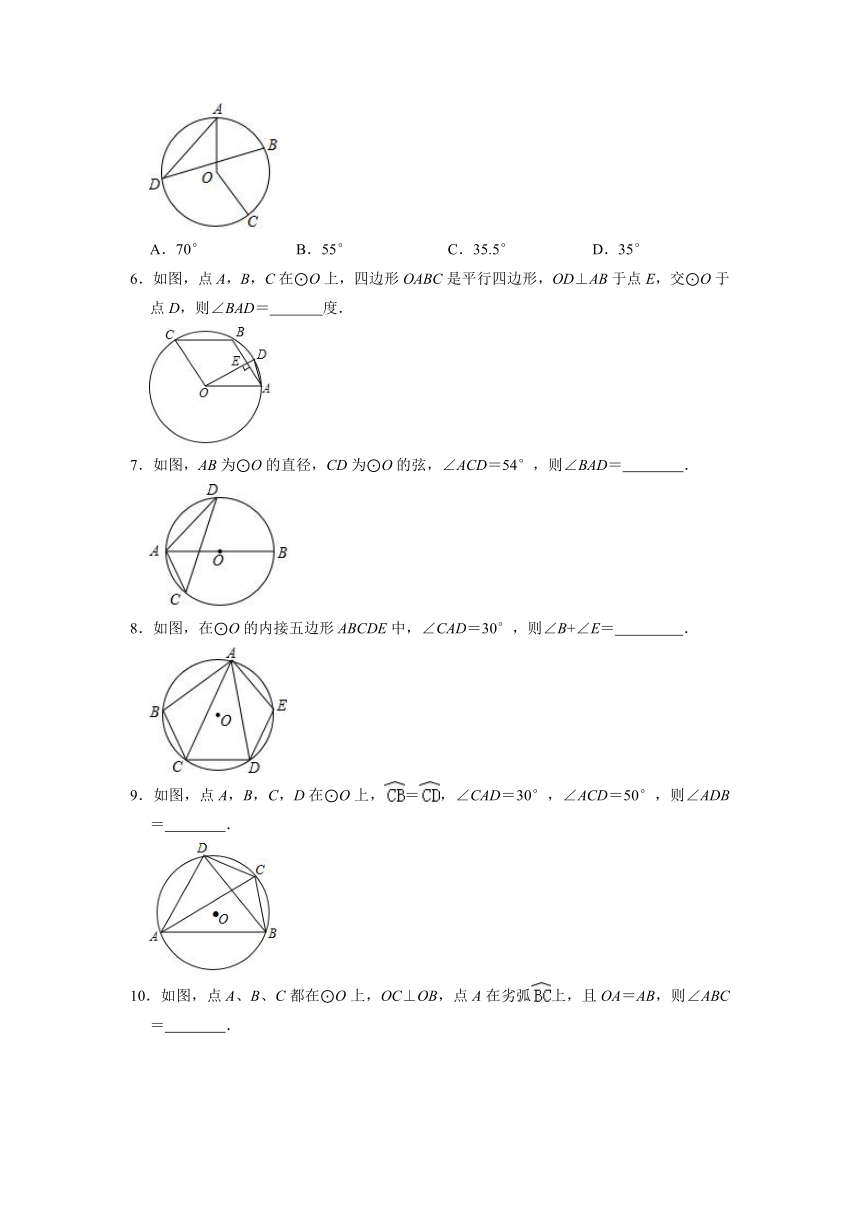
5.如图,点A、B、C、D在⊙O上,∠AOC=140°,点B是的中点,则∠D的度数是( )
A.70° B.55° C.35.5° D.35°
6.如图,点A,B,C在⊙O上,四边形OABC是平行四边形,OD⊥AB于点E,交⊙O于点D,则∠BAD= 度.
7.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD= .
8.如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .
9.如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= .
10.如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧上,且OA=AB,则∠ABC= .
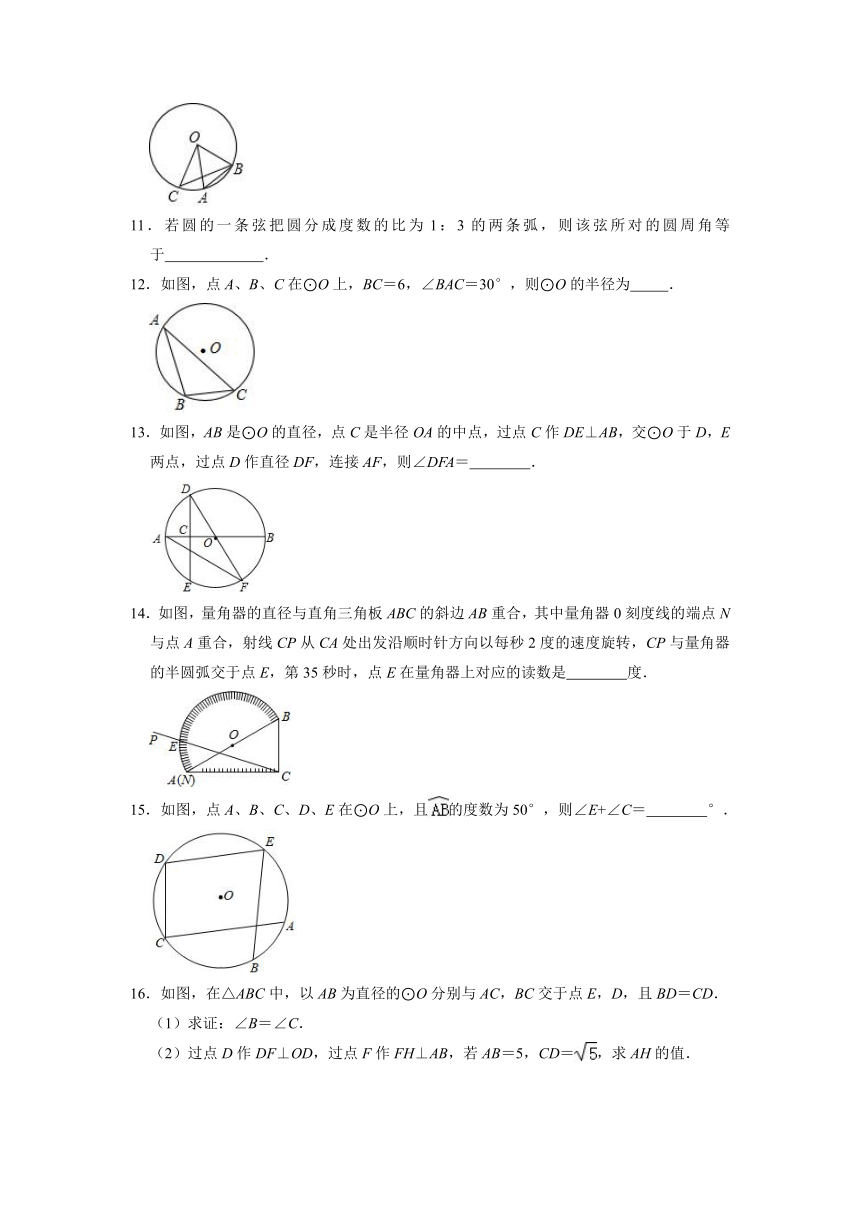
11.若圆的一条弦把圆分成度数的比为1:3的两条弧,则该弦所对的圆周角等于 .
12.如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为 .
13.如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连接AF,则∠DFA= .
14.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35秒时,点E在量角器上对应的读数是 度.
15.如图,点A、B、C、D、E在⊙O上,且的度数为50°,则∠E+∠C= °.
16.如图,在△ABC中,以AB为直径的⊙O分别与AC,BC交于点E,D,且BD=CD.
(1)求证:∠B=∠C.
(2)过点D作DF⊥OD,过点F作FH⊥AB,若AB=5,CD=,求AH的值.
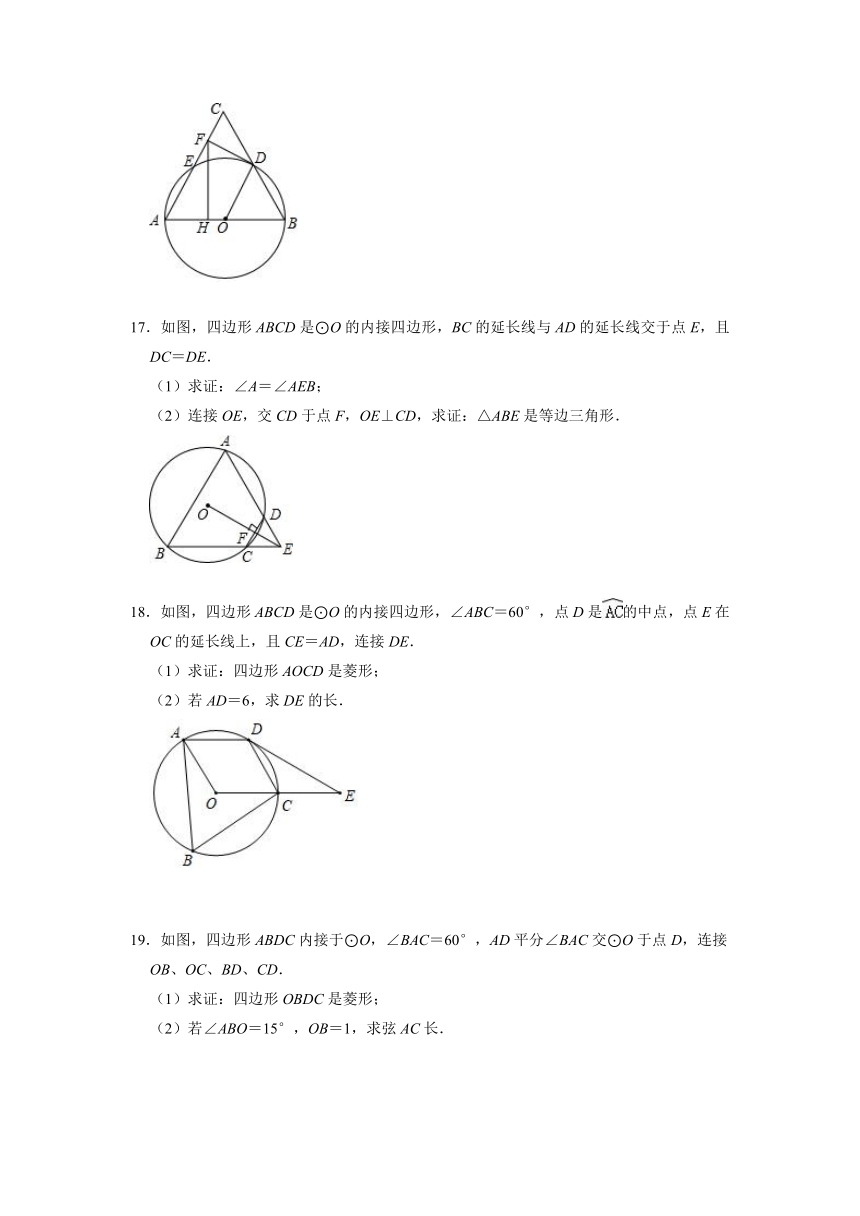
17.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
18.如图,四边形ABCD是⊙O的内接四边形,∠ABC=60°,点D是的中点,点E在OC的延长线上,且CE=AD,连接DE.
(1)求证:四边形AOCD是菱形;
(2)若AD=6,求DE的长.
19.如图,四边形ABDC内接于⊙O,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB、OC、BD、CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=1,求弦AC长.
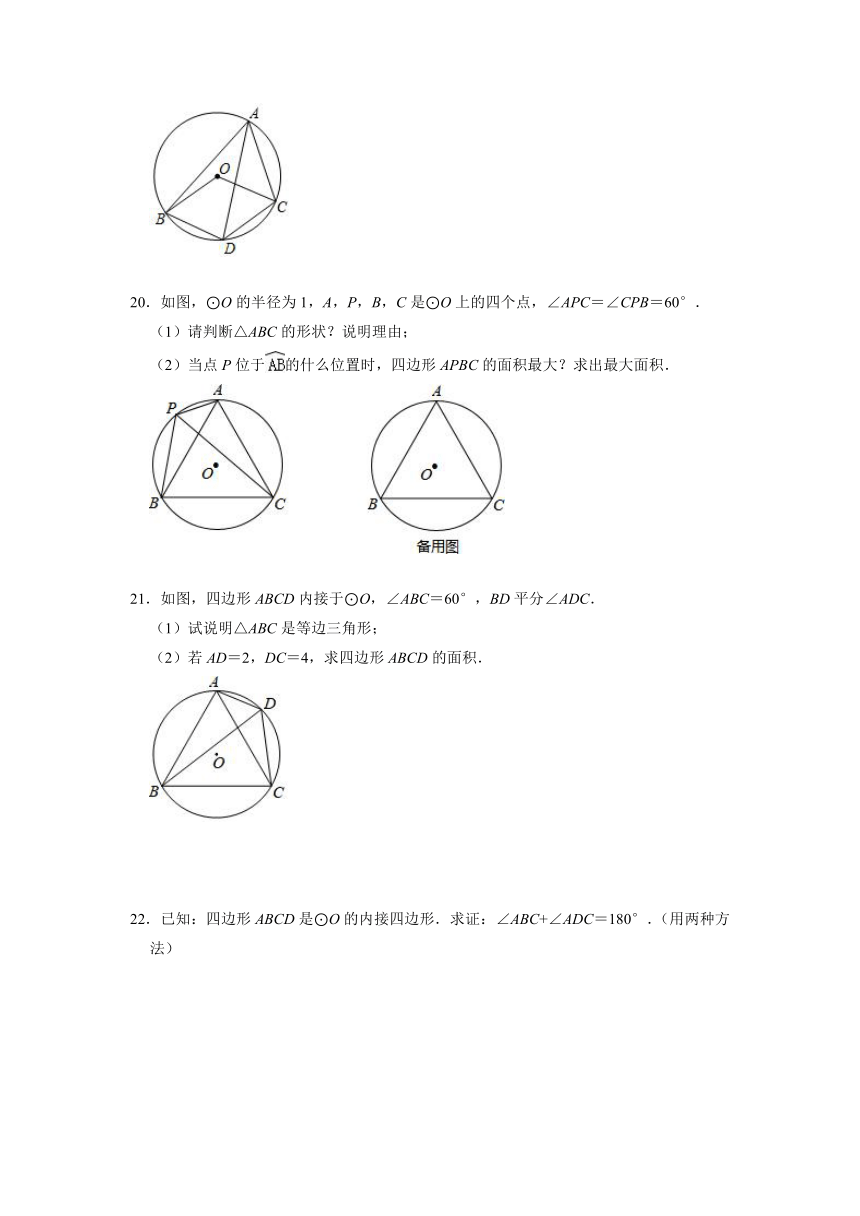
20.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)请判断△ABC的形状?说明理由;
(2)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.
21.如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
22.已知:四边形ABCD是⊙O的内接四边形.求证:∠ABC+∠ADC=180°.(用两种方法)
23.如图,四边形ABCD是⊙O的内接四边形,=,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
参考答案
1.解:连接FB.
∵∠AOF=40°,
∴∠FOB=180°﹣40°=140°,
∴∠FEB=∠FOB=70°
∵EF=EB
∴∠EFB=∠EBF=55°,
∵FO=BO,
∴∠OFB=∠OBF=20°,
∴∠EFO=∠EBO,
∠EFO=∠EFB﹣∠OFB=35°,
故选:B.
2.解:连接PA,PB,PC,过P作PD⊥AB于D,PE⊥OC于E,
∵∠ACB=60°,
∴∠APB=120°,
∵PA=PB,
∴∠PAB=∠PBA=30°,
∵A(﹣5,0),B(1,0),
∴AB=6,
∴AD=BD=3,
∴PD=,PA=PB=PC=2,
∵PD⊥AB,PE⊥OC,∠AOC=90°,
∴四边形PEOD是矩形,
∴OE=PD=,PE=OD=2,
∴CE===2,
∴OC=CE+OE=2+,
∴点C的纵坐标为2+,
故选:B.
3.解:由相交弦定理得:AP×BP=CP×DP,
∵PA=4,PB=6,PD=2,
∴CP=12,
∴DC=12+2=14,
∵CD是⊙O直径,
∴⊙O半径是7.
故选:C.
4.解:由相交弦定理得AP PB=CP PD,
∵AP=6,BP=2,CP=4,
∴PD=AP PB÷CP=6×2÷4=3.
故选:D.
5.解:连接OB,如图所示,
∵点B是的中点,
∴∠AOB=∠AOC=70°,
由圆周角定理得,∠D=∠AOB=35°,
故选:D.
6.解:∵四边形OABC是平行四边形,OC=OA,
∴OA=AB,
∵OD⊥AB,OD过O,
∴AE=BE,=,
即OA=2AE,
∴∠AOD=30°,
∴和的度数是30°
∴∠BAD=15°,
故答案为:15.
7.解:连接BD,如图所示:
∵∠ACD=54°,
∴∠ABD=54°,
∵AB为直径,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABD=36°,
答案为:36°.
8.解:如图,连接CE,
∵五边形ABCDE是圆内接五边形,
∴四边形ABCE是圆内接四边形,
∴∠B+∠AEC=180°,
∵∠CED=∠CAD=30°,
∴∠B+∠E=180°+30°=210°.
故答案为:210°.
9.解:∵=,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ADB=∠ACB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故答案为:70°.
10.解:∵OA=OB,OA=AB,
∴OA=OB=AB,
即△OAB是等边三角形,
∴∠AOB=60°,
∵OC⊥OB,
∴∠COB=90°,
∴∠COA=90°﹣60°=30°,
∴∠ABC=15°,
故答案为:15°
11.解:如图,弦AB将⊙O分成了度数比为1:3两条弧.
连接OA、OB;则∠AOB=90°;
①当所求的圆周角顶点位于D点时,
这条弦所对的圆周角∠ADB=∠AOB=45°;
②当所求的圆周角顶点位于C点时,
这条弦所对的圆周角∠ACB=180°﹣∠ADB=135°.
故答案为:45°,135°.
12.解:∵∠BOC=2∠BAC=60°,又OB=OC,
∴△BOC是等边三角形
∴OB=BC=6,
故答案为6.
13.解:∵点C是半径OA的中点,
∴OC=OD,
∵DE⊥AB,
∴∠CDO=30°,
∴∠DOA=60°,
∴∠DFA=30°,
故答案为:30°.
14.解:连接OE,
∵∠ACB=90°,
∴点C在以AB为直径的圆上,
即点C在⊙O上,
∴∠EOA=2∠ECA,
∵∠ECA=2°×35=70°,
∴∠AOE=2∠ECA=2×70°=140°.
∵量角器0刻度线的端点N与点A重合,
∴点E在量角器上对应的读数是140,
故答案为:140.
15.解:连接EA,
∵为50°,
∴∠BEA=25°,
∵四边形DCAE为⊙O的内接四边形,
∴∠DEA+∠C=180°,
∴∠DEB+∠C=180°﹣25°=155°,
故答案为:155.
16.证明:(1)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵BD=CD,
∴AD是BC的垂直平分线,
∴AB=AC,
∴∠B=∠C;
(2)在Rt△ADB中,AB=5,CD=BD=,
∴AD===2,
∵∠B=∠C,∠DFC=∠ADB=90°,
∴△ADB∽△DFC,
∴,
∴,
∴CF=1,DF=2,
∴AF=AC﹣CF=5﹣1=4,
过O作OG⊥AC于G,
∵∠OGF=∠GFD=∠ODF=90°,
∴四边形OGFD是矩形,
∴OG=DF=2,
∴sin∠FAH=,
∴,FH=,
Rt△AFH中,AH==.
17.证明:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠AEB,
∴∠A=∠AEB;
(2)∵∠A=∠AEB,
∴△ABE是等腰三角形,
∵EO⊥CD,
∴CF=DF,
∴EO是CD的垂直平分线,
∴ED=EC,
∵DC=DE,
∴DC=DE=EC,
∴△DCE是等边三角形,
∴∠AEB=60°,
∴△ABE是等边三角形.
18.证明:(1)∵点D是AC的中点,连接OD,
∴,
∴AD=DC,∠AOD=∠DOC,
∵∠AOC=2∠ABC=120°,
∴∠AOD=∠DOC=60°,
∵OC=OD,
∴OA=OC=CD=AD,
∴四边形AOCD是菱形;
(2)由(1)可知,△COD是等边三角形.
∴∠OCD=∠ODC=60°,
∵CE=AD,CD=AD,
∴CE=CD,
∴∠CDE=∠CED=∠OCD=30°,
∴∠ODE=∠ODC+∠CDE=90°,
在Rt△ODE中,DE=OD tan∠DOE=6×tan60°=6.
19.(1)证明:连接OD,
由圆周角定理得,∠BOC=2∠BAC=120°,
∵AD平分∠BAC,
∴=,
∴∠BOD=∠COD=60°,
∵OB=OD,OC=OD,
∴△BOD和△COD是等边三角形,
∴OB=BD=DC=OC,
∴四边形OBDC是菱形;
(2)解:连接OA,
∵OB=OA,∠ABO=15°,
∴∠AOB=150°,
∴∠AOC=360°﹣150°﹣120°=90°,
∴AC==.
20.解:(1)△ABC是等边三角形.理由如下:
在⊙O中,∵∠BAC与∠CPB是所对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)当点P为的中点时,四边形APBC的面积最大.理由如下:
如图,过点P作PE⊥AB,垂足为E.过点C作CF⊥AB,垂足为F.
∵S△APB=AB PE,S△ABC=AB CF,
∴S四边形APBC=AB (PE+CF),
当点P为的中点时,PE+CF=PC,PC为⊙O的直径,
∴此时四边形APBC的面积最大.
又∵⊙O的半径为1,
∴其内接正三角形的边长AB=,
∴S四边形APBC=×2×=.
21.(1)证明:∵四边形ABCD内接于⊙O.
∴∠ABC+∠ADC=180°,
∵∠ABC=60°,
∴∠ADC=120°,
∵DB平分∠ADC,
∴∠ADB=∠CDB=60°,
∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,
∴∠ABC=∠BCA=∠BAC,
∴△ABC是等边三角形
(2)解:过点A作AE⊥CD,垂足为点E,过点B作BF⊥AC,垂足为点F.
∴∠AED=90°
∵∠ADC=120°,
∴∠ADE=60°,
∴∠DAE=30°,
∴DE=AD=1,AE===,
∵CD=4,
∴CE=CD+DE=1+4=5,
∴S△ACD=CD AE=4×=2,
Rt△AEC中,∠AED=90°,
∴AC===2,
∵△ABC是等边三角形,
∴AB=BC=AC=2,
∴AF=FC=,
∴BF===,
∴S△ABC=×2×=7,
∴四边形ABCD的面积=7+2=9.
22.证法1:连接OA,OC,
∵∠B=∠1,∠D=∠2,
∴∠B+∠D=(∠1+∠2)=×360°=180°;
证法2:如图2,连接CA,BD,
∵∠1=∠2,∠3=∠4,
∴∠ADC=∠1+∠3=∠2+∠4,
∴∠ADC+∠ABC=∠2+∠4+∠ABC=180°.
23.(1)证明:∵四边形ABCD是⊙O内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
∵=,
∴∠BAD=∠ACD,
∴∠DCE=∠ACD,
∴CD平分∠ACE;
(2)解:∵AC为直径,
∴∠ADC=90°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠DEC=∠ADC,
∵∠DCE=∠ACD,
∴△DCE∽△ACD,
∴=,即=,
∴CD=3.
优生辅导训练(附答案)
1.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
A.20° B.35° C.40° D.55°
2.如图,⊙P与x轴交于点A(﹣5,0),B(1,0),与y轴的正半轴交于点C.若∠ACB=60°,则点C的纵坐标为( )
A.+ B.2+ C.4 D.2+2
3.如图,⊙O中,弦AB与直径CD相交于点P,且PA=4,PB=6,PD=2,则⊙O的半径为( )
A.9 B.8 C.7 D.6
4.如图所示,已知⊙O中,弦AB,CD相交于点P,AP=6,BP=2,CP=4,则PD的长是( )
A.6 B.5 C.4 D.3
5.如图,点A、B、C、D在⊙O上,∠AOC=140°,点B是的中点,则∠D的度数是( )
A.70° B.55° C.35.5° D.35°
6.如图,点A,B,C在⊙O上,四边形OABC是平行四边形,OD⊥AB于点E,交⊙O于点D,则∠BAD= 度.
7.如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD= .
8.如图,在⊙O的内接五边形ABCDE中,∠CAD=30°,则∠B+∠E= .
9.如图,点A,B,C,D在⊙O上,=,∠CAD=30°,∠ACD=50°,则∠ADB= .
10.如图,点A、B、C都在⊙O上,OC⊥OB,点A在劣弧上,且OA=AB,则∠ABC= .
11.若圆的一条弦把圆分成度数的比为1:3的两条弧,则该弦所对的圆周角等于 .
12.如图,点A、B、C在⊙O上,BC=6,∠BAC=30°,则⊙O的半径为 .
13.如图,AB是⊙O的直径,点C是半径OA的中点,过点C作DE⊥AB,交⊙O于D,E两点,过点D作直径DF,连接AF,则∠DFA= .
14.如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器0刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35秒时,点E在量角器上对应的读数是 度.
15.如图,点A、B、C、D、E在⊙O上,且的度数为50°,则∠E+∠C= °.
16.如图,在△ABC中,以AB为直径的⊙O分别与AC,BC交于点E,D,且BD=CD.
(1)求证:∠B=∠C.
(2)过点D作DF⊥OD,过点F作FH⊥AB,若AB=5,CD=,求AH的值.
17.如图,四边形ABCD是⊙O的内接四边形,BC的延长线与AD的延长线交于点E,且DC=DE.
(1)求证:∠A=∠AEB;
(2)连接OE,交CD于点F,OE⊥CD,求证:△ABE是等边三角形.
18.如图,四边形ABCD是⊙O的内接四边形,∠ABC=60°,点D是的中点,点E在OC的延长线上,且CE=AD,连接DE.
(1)求证:四边形AOCD是菱形;
(2)若AD=6,求DE的长.
19.如图,四边形ABDC内接于⊙O,∠BAC=60°,AD平分∠BAC交⊙O于点D,连接OB、OC、BD、CD.
(1)求证:四边形OBDC是菱形;
(2)若∠ABO=15°,OB=1,求弦AC长.
20.如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)请判断△ABC的形状?说明理由;
(2)当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.
21.如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
22.已知:四边形ABCD是⊙O的内接四边形.求证:∠ABC+∠ADC=180°.(用两种方法)
23.如图,四边形ABCD是⊙O的内接四边形,=,AC为直径,DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
参考答案
1.解:连接FB.
∵∠AOF=40°,
∴∠FOB=180°﹣40°=140°,
∴∠FEB=∠FOB=70°
∵EF=EB
∴∠EFB=∠EBF=55°,
∵FO=BO,
∴∠OFB=∠OBF=20°,
∴∠EFO=∠EBO,
∠EFO=∠EFB﹣∠OFB=35°,
故选:B.
2.解:连接PA,PB,PC,过P作PD⊥AB于D,PE⊥OC于E,
∵∠ACB=60°,
∴∠APB=120°,
∵PA=PB,
∴∠PAB=∠PBA=30°,
∵A(﹣5,0),B(1,0),
∴AB=6,
∴AD=BD=3,
∴PD=,PA=PB=PC=2,
∵PD⊥AB,PE⊥OC,∠AOC=90°,
∴四边形PEOD是矩形,
∴OE=PD=,PE=OD=2,
∴CE===2,
∴OC=CE+OE=2+,
∴点C的纵坐标为2+,
故选:B.
3.解:由相交弦定理得:AP×BP=CP×DP,
∵PA=4,PB=6,PD=2,
∴CP=12,
∴DC=12+2=14,
∵CD是⊙O直径,
∴⊙O半径是7.
故选:C.
4.解:由相交弦定理得AP PB=CP PD,
∵AP=6,BP=2,CP=4,
∴PD=AP PB÷CP=6×2÷4=3.
故选:D.
5.解:连接OB,如图所示,
∵点B是的中点,
∴∠AOB=∠AOC=70°,
由圆周角定理得,∠D=∠AOB=35°,
故选:D.
6.解:∵四边形OABC是平行四边形,OC=OA,
∴OA=AB,
∵OD⊥AB,OD过O,
∴AE=BE,=,
即OA=2AE,
∴∠AOD=30°,
∴和的度数是30°
∴∠BAD=15°,
故答案为:15.
7.解:连接BD,如图所示:
∵∠ACD=54°,
∴∠ABD=54°,
∵AB为直径,
∴∠ADB=90°,
∴∠BAD=90°﹣∠ABD=36°,
答案为:36°.
8.解:如图,连接CE,
∵五边形ABCDE是圆内接五边形,
∴四边形ABCE是圆内接四边形,
∴∠B+∠AEC=180°,
∵∠CED=∠CAD=30°,
∴∠B+∠E=180°+30°=210°.
故答案为:210°.
9.解:∵=,∠CAD=30°,
∴∠CAD=∠CAB=30°,
∴∠DBC=∠DAC=30°,
∵∠ACD=50°,
∴∠ABD=50°,
∴∠ADB=∠ACB=180°﹣∠CAB﹣∠ABC=180°﹣50°﹣30°﹣30°=70°.
故答案为:70°.
10.解:∵OA=OB,OA=AB,
∴OA=OB=AB,
即△OAB是等边三角形,
∴∠AOB=60°,
∵OC⊥OB,
∴∠COB=90°,
∴∠COA=90°﹣60°=30°,
∴∠ABC=15°,
故答案为:15°
11.解:如图,弦AB将⊙O分成了度数比为1:3两条弧.
连接OA、OB;则∠AOB=90°;
①当所求的圆周角顶点位于D点时,
这条弦所对的圆周角∠ADB=∠AOB=45°;
②当所求的圆周角顶点位于C点时,
这条弦所对的圆周角∠ACB=180°﹣∠ADB=135°.
故答案为:45°,135°.
12.解:∵∠BOC=2∠BAC=60°,又OB=OC,
∴△BOC是等边三角形
∴OB=BC=6,
故答案为6.
13.解:∵点C是半径OA的中点,
∴OC=OD,
∵DE⊥AB,
∴∠CDO=30°,
∴∠DOA=60°,
∴∠DFA=30°,
故答案为:30°.
14.解:连接OE,
∵∠ACB=90°,
∴点C在以AB为直径的圆上,
即点C在⊙O上,
∴∠EOA=2∠ECA,
∵∠ECA=2°×35=70°,
∴∠AOE=2∠ECA=2×70°=140°.
∵量角器0刻度线的端点N与点A重合,
∴点E在量角器上对应的读数是140,
故答案为:140.
15.解:连接EA,
∵为50°,
∴∠BEA=25°,
∵四边形DCAE为⊙O的内接四边形,
∴∠DEA+∠C=180°,
∴∠DEB+∠C=180°﹣25°=155°,
故答案为:155.
16.证明:(1)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴AD⊥BC,
∵BD=CD,
∴AD是BC的垂直平分线,
∴AB=AC,
∴∠B=∠C;
(2)在Rt△ADB中,AB=5,CD=BD=,
∴AD===2,
∵∠B=∠C,∠DFC=∠ADB=90°,
∴△ADB∽△DFC,
∴,
∴,
∴CF=1,DF=2,
∴AF=AC﹣CF=5﹣1=4,
过O作OG⊥AC于G,
∵∠OGF=∠GFD=∠ODF=90°,
∴四边形OGFD是矩形,
∴OG=DF=2,
∴sin∠FAH=,
∴,FH=,
Rt△AFH中,AH==.
17.证明:(1)∵四边形ABCD是⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠A=∠DCE,
∵DC=DE,
∴∠DCE=∠AEB,
∴∠A=∠AEB;
(2)∵∠A=∠AEB,
∴△ABE是等腰三角形,
∵EO⊥CD,
∴CF=DF,
∴EO是CD的垂直平分线,
∴ED=EC,
∵DC=DE,
∴DC=DE=EC,
∴△DCE是等边三角形,
∴∠AEB=60°,
∴△ABE是等边三角形.
18.证明:(1)∵点D是AC的中点,连接OD,
∴,
∴AD=DC,∠AOD=∠DOC,
∵∠AOC=2∠ABC=120°,
∴∠AOD=∠DOC=60°,
∵OC=OD,
∴OA=OC=CD=AD,
∴四边形AOCD是菱形;
(2)由(1)可知,△COD是等边三角形.
∴∠OCD=∠ODC=60°,
∵CE=AD,CD=AD,
∴CE=CD,
∴∠CDE=∠CED=∠OCD=30°,
∴∠ODE=∠ODC+∠CDE=90°,
在Rt△ODE中,DE=OD tan∠DOE=6×tan60°=6.
19.(1)证明:连接OD,
由圆周角定理得,∠BOC=2∠BAC=120°,
∵AD平分∠BAC,
∴=,
∴∠BOD=∠COD=60°,
∵OB=OD,OC=OD,
∴△BOD和△COD是等边三角形,
∴OB=BD=DC=OC,
∴四边形OBDC是菱形;
(2)解:连接OA,
∵OB=OA,∠ABO=15°,
∴∠AOB=150°,
∴∠AOC=360°﹣150°﹣120°=90°,
∴AC==.
20.解:(1)△ABC是等边三角形.理由如下:
在⊙O中,∵∠BAC与∠CPB是所对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
(2)当点P为的中点时,四边形APBC的面积最大.理由如下:
如图,过点P作PE⊥AB,垂足为E.过点C作CF⊥AB,垂足为F.
∵S△APB=AB PE,S△ABC=AB CF,
∴S四边形APBC=AB (PE+CF),
当点P为的中点时,PE+CF=PC,PC为⊙O的直径,
∴此时四边形APBC的面积最大.
又∵⊙O的半径为1,
∴其内接正三角形的边长AB=,
∴S四边形APBC=×2×=.
21.(1)证明:∵四边形ABCD内接于⊙O.
∴∠ABC+∠ADC=180°,
∵∠ABC=60°,
∴∠ADC=120°,
∵DB平分∠ADC,
∴∠ADB=∠CDB=60°,
∴∠ACB=∠ADB=60°,∠BAC=∠CDB=60°,
∴∠ABC=∠BCA=∠BAC,
∴△ABC是等边三角形
(2)解:过点A作AE⊥CD,垂足为点E,过点B作BF⊥AC,垂足为点F.
∴∠AED=90°
∵∠ADC=120°,
∴∠ADE=60°,
∴∠DAE=30°,
∴DE=AD=1,AE===,
∵CD=4,
∴CE=CD+DE=1+4=5,
∴S△ACD=CD AE=4×=2,
Rt△AEC中,∠AED=90°,
∴AC===2,
∵△ABC是等边三角形,
∴AB=BC=AC=2,
∴AF=FC=,
∴BF===,
∴S△ABC=×2×=7,
∴四边形ABCD的面积=7+2=9.
22.证法1:连接OA,OC,
∵∠B=∠1,∠D=∠2,
∴∠B+∠D=(∠1+∠2)=×360°=180°;
证法2:如图2,连接CA,BD,
∵∠1=∠2,∠3=∠4,
∴∠ADC=∠1+∠3=∠2+∠4,
∴∠ADC+∠ABC=∠2+∠4+∠ABC=180°.
23.(1)证明:∵四边形ABCD是⊙O内接四边形,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠DCE=180°,
∴∠DCE=∠BAD,
∵=,
∴∠BAD=∠ACD,
∴∠DCE=∠ACD,
∴CD平分∠ACE;
(2)解:∵AC为直径,
∴∠ADC=90°,
∵DE⊥BC,
∴∠DEC=90°,
∴∠DEC=∠ADC,
∵∠DCE=∠ACD,
∴△DCE∽△ACD,
∴=,即=,
∴CD=3.
