2021-2022学年北师大版九年级数学下册3.5确定圆的条件 解答题专题训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.5确定圆的条件 解答题专题训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 481.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 11:05:01 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.5确定圆的条件》解答题专题训练(附答案)
1.已知:如图,在△ABC中,点D是∠BAC的角平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.求证:点E是过A,B,D三点的圆的圆心.
2.已知:如图,△ABC内接于⊙O,AD为⊙O的弦,∠1=∠2,DE⊥AB于E,DF⊥AC于F.求证:BE=CF.
3.如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且DA的延长线与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.
(1)判断△FBC的形状,并说明理由;
(2)请给出一个能反映AB、AC和FA之间数量关系的一个等式,并说明你给出的等式成立.
4.将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.
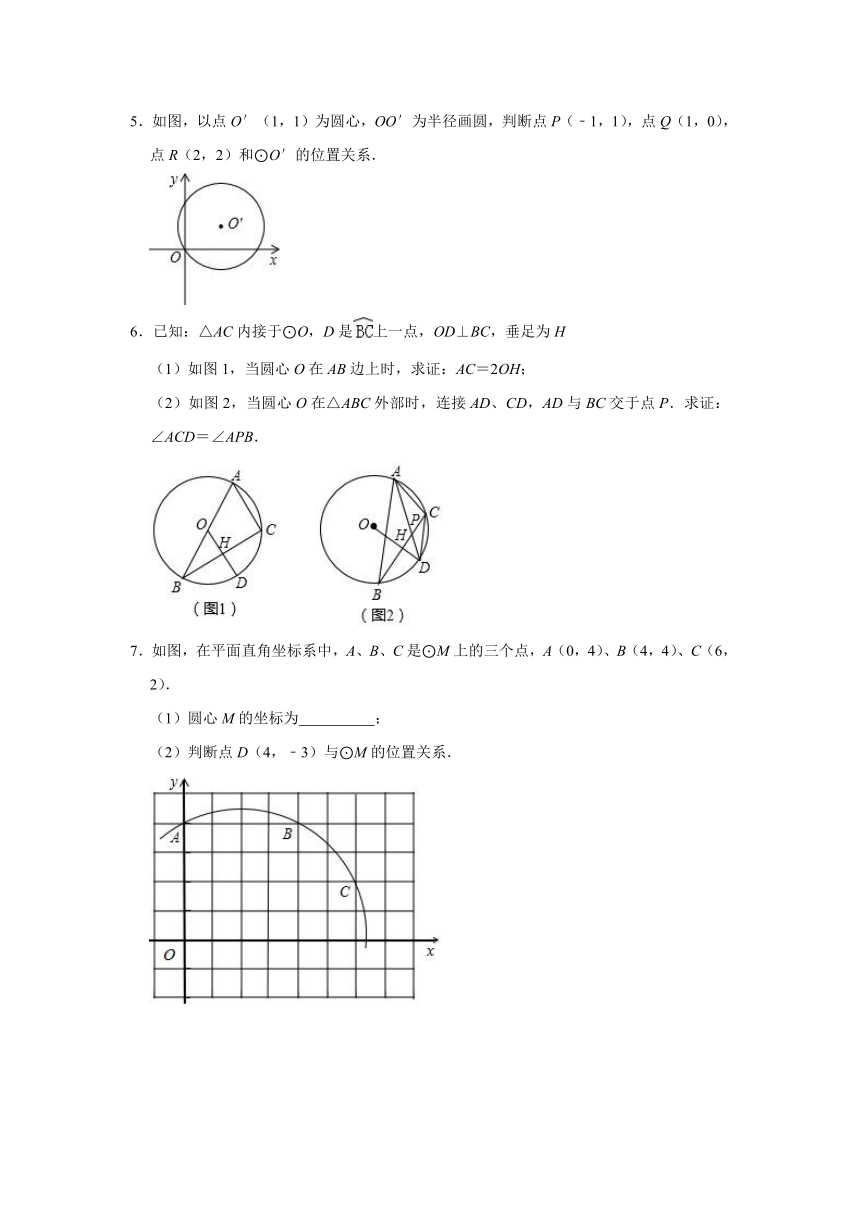
5.如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(﹣1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系.
6.已知:△AC内接于⊙O,D是上一点,OD⊥BC,垂足为H
(1)如图1,当圆心O在AB边上时,求证:AC=2OH;
(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P.求证:∠ACD=∠APB.
7.如图,在平面直角坐标系中,A、B、C是⊙M上的三个点,A(0,4)、B(4,4)、C(6,2).
(1)圆心M的坐标为 ;
(2)判断点D(4,﹣3)与⊙M的位置关系.
8.如图1,⊙O是△ABC的外接圆,连接AO,若∠BAC+∠OAB=90°.
(1)求证:=
(2)如图2,作CD⊥AB交于D,AO的延长线交CD于E,若AO=3,AE=4,求线段AC的长.
9.如图,在矩形ABCD中,AB=5,AD=a(a>5).点P在以A为圆心、AB长为半径的⊙A上,且在矩形ABCD的内部,P到AD、CD的距离PE、PF相等.
(1)若a=7,求AE长;
(2)若⊙A上满足条件的点P只有一个,求a的值;
(3)若⊙A上满足条件的点P有两个,求a的取值范围.
10.小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=;他还证明了线段P1P2的中点P(x,y)的坐标公式是:x=,y=;
启发应用
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A、B.
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由.
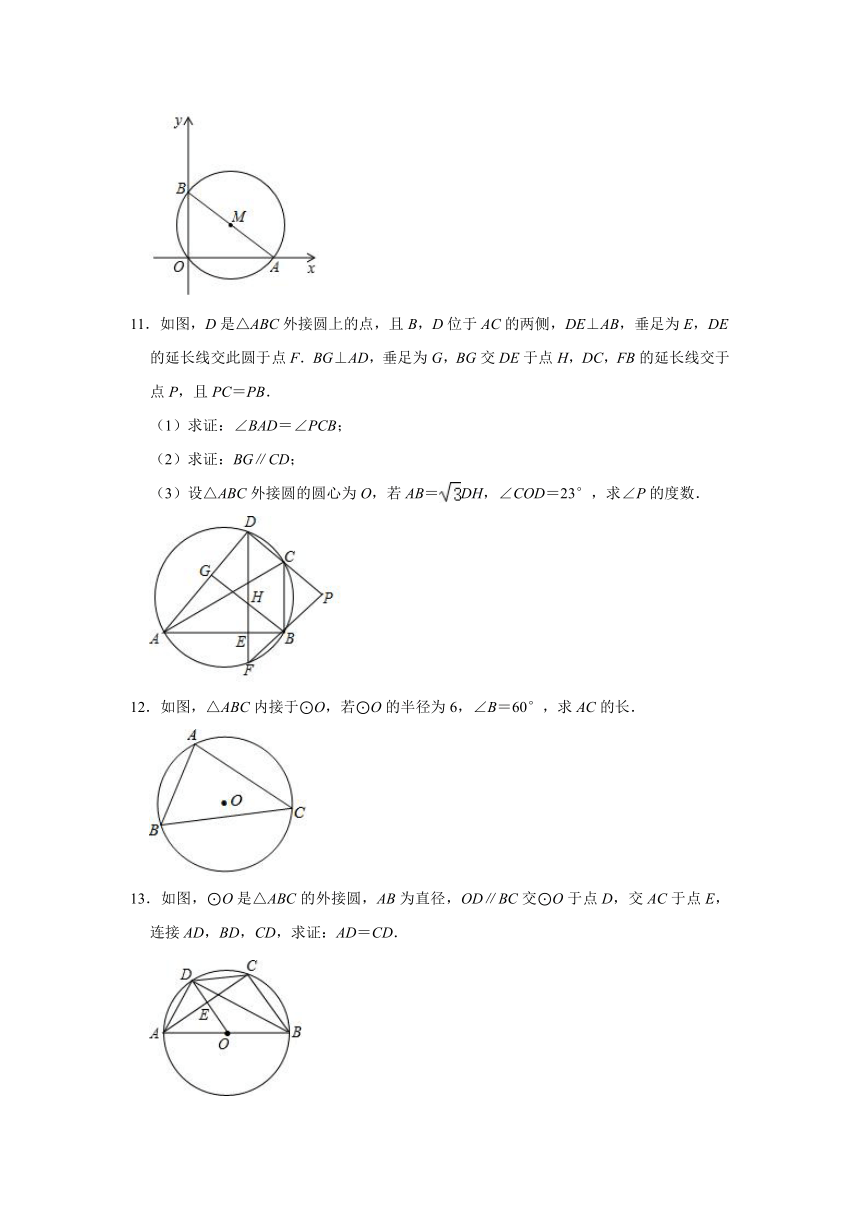
11.如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=DH,∠COD=23°,求∠P的度数.
12.如图,△ABC内接于⊙O,若⊙O的半径为6,∠B=60°,求AC的长.
13.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD,求证:AD=CD.
14.如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=∠DAC,求AC的长.
15.如图,⊙O是Rt△ABC的外接圆,AC=BC,∠CAB的平分线AD交BC于点E、交⊙O于点D,延长BD交AC的延长线于点F,连接CD、OG平分CD.
(1)求证:AF=AB;
(2)求证:2OG=AD;
(3)若CD=4﹣2,求⊙O的面积.
16.如图所示,⊙O是△ABC的外接圆,AB是直径,∠ABC=30°,点E是OC的中点,连接AE并延长交⊙〇于点D,连接OD,CD,BD.
(1)求证:△AEO≌△DEC;
(2)若AB=12,则四边形AODC的面积是 .
17.如图,△ABC是⊙O的内接三角形,∠BAD是△ABC的一个外角,∠BAC、∠BAD的平分线分别交⊙O于点E、F.请你在图上连接EF.
(1)证明:EF是⊙O的直径;
(2)请你判断EF与BC有怎样的位置关系?并请证明你的结论.
18.如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.
(1)求⊙P的半径及圆心P的坐标;
(2)M为劣弧的中点,求证:AM是∠OAB的平分线.
19.如图,在钝角△ABC中,∠C=45°,AE⊥BC,垂足为E点,且AB与AC的长度为方程x2﹣9x+18=0的两个根,⊙O是△ABC的外接圆.
求:(1)⊙O的半径;
(2)BE的长.
20.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°,BC=时,求⊙O的半径.
21.(1)如图(1),AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
(2)如图(2),⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
22.如图,在平面直角坐标系内,已知点A(2,2),B(﹣6,﹣4),C(2,﹣4).
(1)求△ABC的外接圆的圆心点M的坐标;
(2)求△ABC的外接圆在x轴上所截弦DE的长.
参考答案
1.证明:∵点D在∠BAC的平分线上,
∴∠1=∠2.(1分)
又∵DE∥AC,
∴∠2=∠3,
∴∠1=∠3.(2分)
∴AE=DE.(3分)
又∵BD⊥AD于点D,
∴∠ADB=90°.(4分)
∴∠EBD+∠1=∠EDB+∠3=90°.(5分)
∴∠EBD=∠EDB.(6分)
∴BE=DE.(7分)
∴AE=BE=DE.(8分)
∴点E是A,B,D所在的圆的圆心.(10分)
2.证明:连接DB、DF,
∵∠A的平分线AD交圆于D,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,∠DFB=∠DFC=90°,∠BAD=∠CAD,
∴DB=DC,
∴在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
3.解:(1)△FBC是等边三角形,
∵∠CAM=120°,AD是∠CAM的平分线,
∴∠MAD=∠CAD=60°,
∵四边形AFBC是圆内接四边形,
∴∠FBC=∠CAD=60°,又∠BCF=∠FAB=∠MAD=60°,
∴△FBC是等边三角形;
(2)AB=AC+FA.
理由如下:在AB上截取AH=AC,
∵∠HAC=∠BFC=60°,
∴△AHC是等边三角形,
∴∠ACH=60°,CA=CH,
∵∠FCB=60°,
∴∠BCH=∠FCA,
在△BCH和△FCA中,
,
∴△BCH≌△FCA,
∴BH=FA,
∴AB=BH+AH=FA+AC.
4.解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,BC,BC交OA于D.
∵BC=16cm,
∴BD=8cm,
∵AB=10cm,
∴AD=6cm,
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:R=cm,
∴圆片的半径R为cm.
5.解:∵OO′=r==,O′P==2
同理可得:O′Q=1,O′R=,
∴O′P>r,点P在⊙O′外;
O′Q<r,点Q在⊙O′内;
O′R=r,点R在⊙O′上.
6.(1)证明:∵OD⊥BC,
∴BH=HC,
∵OA=OB,
∴AC=2OH.
(2)证明:∵OD⊥BC,
∴=,
∴∠BAD=∠DAC,
∵∠B=∠ADC,∠APB+∠BAD+∠B=180°,∠DAC+∠ACD+∠ADC=180°,
∴∠APB=∠ACD.
7.解:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,0)
故答案为:2,0.
(2)圆的半径AM==2,
线段MD==<2,
所以点D在⊙M内.
8.(1)证明:连BO并延长BO交AC于T.
∵AO=BO,
∴∠OAB=∠OBA,
又∵∠BAC+∠OAB=90°,
∴∠BAC+∠OBA=90°,
∴∠BTA=90°,
∴BT⊥AC,
∴=.
(2)延长AO并交⊙O于F,连接CF.
∵CD⊥AB于D,
∴∠CDA=90°,
∴∠OAB+∠AED=90°,
∵∠OAB+∠BAC=90°,
∴∠AED=∠BAC=∠FEC,
∵AF为⊙O直径,
∴∠ACF=90°,
同理:∠FCE=∠BAC,
∴∠FEC=∠FCE,
∴FE=FC,
∵AO=3,AE=4,
∴OE=1,FE=FC=2,
在Rt△FCA中
∴AC==4
9.解:(1)连接AP,
设AE=x,则(7﹣x)2+x2=25,
解得x=3或4
所以AE的长为3或4;
(2)当△APD是等腰直角三角形时,⊙A上满足条件的点P只有一个,
此时AD=AP=5
(3)观察图象可知:当5<a<5时,存在两个点P满足条件;
10.解:(1)∵∠AOB=90°,
∴AB是⊙M的直径,
∵A(8,0),B(0,6),
∴AB==10,
∴⊙M的半径为5,
由线段中点坐标公式x=,y=,得x=4,y=3,
∴M(4,3),
(2)点C在⊙M上,
理由:∵C(1,7),M(4,3),
∴CM==5,
∴点C在⊙M上.
11.(1)证明:如图1,
∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB;
(2)证明:由(1)得∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∵∠ABC=90°,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(3)解:由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
在Rt△ABC中,
∵AB=DH,
∴tan∠ACB==,
∴∠ACB=60°,
连接OD,
∵∠COD=23°,OD=OC,
∴∠OCD=(180°﹣23°)=()°,
∴∠PCB=180°﹣∠ACB﹣∠OCD=()°,
∵PC=PB,
∴∠P=180°﹣2×()°=97°.
12.解:如图,作直径AD,连接CD.
∴∠ACD=90°.
∵∠B=60°,
∴∠D=∠B=60°.
∵⊙O的半径为6,
∴AD=12.
在Rt△ACD中,∠CAD=30°,
∴CD=6.
∴AC=6.
13.证明:∵OD=OB,
∴∠ODB=∠OBD,
∵OD∥BC,
∴∠ODB=∠DBC,
∴∠DBC=∠OBD,
∴∠DAC=∠DCA,
∴AD=CD.
14.解:连接CD,
∵∠ABC=∠DAC,
∴=,
∴AC=CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴AC=AD=6.
15.(1)证明:∵AB是⊙O的直径,
∴∠ADB=∠ADF=90°,
∵AD平分∠CAB,
∴∠FAD=∠BAD,
在△ADF和△ADB中,
,
∴△FAD≌△BAD,
∴AF=AB.
(2)连接OD,作OM⊥BD,则DM=BM,
∵OA=OB,
∴OM∥AD,AD=2OM,
∵AD平分∠CAB,
∴∠DAC=∠DAB,
∴=,
∴CD=BD,
∵OG平分CD,
∴OG⊥CD,DG=CG,
∴DG=DM,
在Rt△ODG和Rt△ODM中,
,
∴△ODG≌△ODM(HL),
∴OG=OM,
∴2OG=AD.
(3)∵CD为Rt△CBF斜边上的中线,
∴BF=2CD=2(4﹣2)=8﹣4,
设OA=r,则AF=AB=2r,AC=BC=r,
∴CF=(2﹣)r,
在Rt△BCF中,∵BC2+CF2=BF2,
∴(r)2+[(2﹣)r]2=(8﹣4)2,
∴r2=8﹣4,
∴⊙O的面积为(8﹣4)π.
16.(1)证明:∵AB是直径,∠ABC=30°,
∴∠ACB=90°,∠CAO=60°,
∵OA=OC,
∴△ACO是等边三角形,
∵CE=EO,
∴AE⊥CO,∠CAE=∠EAO=30°,
∵∠CDE=∠ABC=30°,
∴∠CDE=∠EAO,
在△CED和△OEA中,
,
∴△AEO≌△DEC.
(2)连接DO.
∵△AEO≌△DEC.∠CDE=∠EAO
∴CD=AO,CD∥AO,
∴四边形AODC是平行四边形,
∴S平行四边形AODC=2 S△ACO=2××62=18.
故答案为18.
17.解:(1)∵AF平分∠BAD,AE平分∠BAC,
∴∠BAF=∠BAD,∠BAE=∠BAC,
∴∠BAF+∠BAE=(∠BAD+∠BAC)=×180°=90°,即∠EAF=90°,
∴EF为⊙O的直径;
(2)∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴=,
∴EF垂直平分BC.
18.解:(1)∵∠AOB=90°,
∴线段AB是⊙P的直径,
∵A(0,﹣6),B(8,0),PA=PB,
∴P(4,﹣3).
(2)∵=,
∴∠OAM=∠MAB,
∴AM是∠OAB的平分线.
19.解:(1)连接OB,
解方程x2﹣9x+18=0,
得,x1=3,x2=6,
由图形可知,AC=3,AB=6,
由圆周角定理得,∠AOB=2∠C=90°,
∴△AOB为等腰直角三角形,
∴OB=AB=3;
(2)∵∠C=45°,AE⊥BC,
∴△AEC为等腰直角三角形,
∴AE=AC=,
∴BE==.
20.(1)证明:∵OD⊥AC,
∴=,
∴∠CBD=∠DBA,
∴BD平分∠ABC;
(2)∵OD=OB,
∴∠OBD=∠ODB=30°,
∴∠ABC=60°,
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,∠A=30°,BC=,
∴AB=2BC=2,
∴⊙O的半径为.
21.证明:(1)∵∠1=∠2,
∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF,
∵AB=CB,BE=BF,
∴△ABE≌△CBF(SAS);
(2)在圆O中,∵∠A=45°,=,
∴∠D=45°,
∵BD为圆的直径,
∴∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BC=BD sin45°,
∵BD=2,
∴BC=.
22.解:(1)∵B(﹣6,﹣4),C(2,﹣4),
∴线段BC的垂直平分线是x=﹣2,
∵A(2,2),C(2,﹣4),
∴线段AC的垂直平分线是y=﹣1,
∴△ABC的外接圆的圆心M的坐标为:(﹣2,﹣1);
(2)连接OM,作MN⊥DE于N,
由题意得,AC=6,BC=8,
由勾股定理得,AB=10,
则DN==2,
由垂径定理得,DE=2DN=4.
1.已知:如图,在△ABC中,点D是∠BAC的角平分线上一点,BD⊥AD于点D,过点D作DE∥AC交AB于点E.求证:点E是过A,B,D三点的圆的圆心.
2.已知:如图,△ABC内接于⊙O,AD为⊙O的弦,∠1=∠2,DE⊥AB于E,DF⊥AC于F.求证:BE=CF.
3.如图,已知△ABC的一个外角∠CAM=120°,AD是∠CAM的平分线,且DA的延长线与△ABC的外接圆交于F,连接FB、FC,且FC与AB交于E.
(1)判断△FBC的形状,并说明理由;
(2)请给出一个能反映AB、AC和FA之间数量关系的一个等式,并说明你给出的等式成立.
4.将图中的破轮子复原,已知弧上三点A,B,C.
(1)画出该轮的圆心;
(2)若△ABC是等腰三角形,底边BC=16cm,腰AB=10cm,求圆片的半径R.
5.如图,以点O′(1,1)为圆心,OO′为半径画圆,判断点P(﹣1,1),点Q(1,0),点R(2,2)和⊙O′的位置关系.
6.已知:△AC内接于⊙O,D是上一点,OD⊥BC,垂足为H
(1)如图1,当圆心O在AB边上时,求证:AC=2OH;
(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P.求证:∠ACD=∠APB.
7.如图,在平面直角坐标系中,A、B、C是⊙M上的三个点,A(0,4)、B(4,4)、C(6,2).
(1)圆心M的坐标为 ;
(2)判断点D(4,﹣3)与⊙M的位置关系.
8.如图1,⊙O是△ABC的外接圆,连接AO,若∠BAC+∠OAB=90°.
(1)求证:=
(2)如图2,作CD⊥AB交于D,AO的延长线交CD于E,若AO=3,AE=4,求线段AC的长.
9.如图,在矩形ABCD中,AB=5,AD=a(a>5).点P在以A为圆心、AB长为半径的⊙A上,且在矩形ABCD的内部,P到AD、CD的距离PE、PF相等.
(1)若a=7,求AE长;
(2)若⊙A上满足条件的点P只有一个,求a的值;
(3)若⊙A上满足条件的点P有两个,求a的取值范围.
10.小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用勾股定理得到结论:P1P2=;他还证明了线段P1P2的中点P(x,y)的坐标公式是:x=,y=;
启发应用
请利用上面的信息,解答下面的问题:
如图,在平面直角坐标系中,已知A(8,0),B(0,6),C(1,7),⊙M经过原点O及点A、B.
(1)求⊙M的半径及圆心M的坐标;
(2)判断点C与⊙M的位置关系,并说明理由.
11.如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AB=DH,∠COD=23°,求∠P的度数.
12.如图,△ABC内接于⊙O,若⊙O的半径为6,∠B=60°,求AC的长.
13.如图,⊙O是△ABC的外接圆,AB为直径,OD∥BC交⊙O于点D,交AC于点E,连接AD,BD,CD,求证:AD=CD.
14.如图,⊙O是△ABC的外接圆,直径AD=12,∠ABC=∠DAC,求AC的长.
15.如图,⊙O是Rt△ABC的外接圆,AC=BC,∠CAB的平分线AD交BC于点E、交⊙O于点D,延长BD交AC的延长线于点F,连接CD、OG平分CD.
(1)求证:AF=AB;
(2)求证:2OG=AD;
(3)若CD=4﹣2,求⊙O的面积.
16.如图所示,⊙O是△ABC的外接圆,AB是直径,∠ABC=30°,点E是OC的中点,连接AE并延长交⊙〇于点D,连接OD,CD,BD.
(1)求证:△AEO≌△DEC;
(2)若AB=12,则四边形AODC的面积是 .
17.如图,△ABC是⊙O的内接三角形,∠BAD是△ABC的一个外角,∠BAC、∠BAD的平分线分别交⊙O于点E、F.请你在图上连接EF.
(1)证明:EF是⊙O的直径;
(2)请你判断EF与BC有怎样的位置关系?并请证明你的结论.
18.如图,在平面直角坐标系中,O(0,0),A(0,﹣6),B(8,0)三点在⊙P上.
(1)求⊙P的半径及圆心P的坐标;
(2)M为劣弧的中点,求证:AM是∠OAB的平分线.
19.如图,在钝角△ABC中,∠C=45°,AE⊥BC,垂足为E点,且AB与AC的长度为方程x2﹣9x+18=0的两个根,⊙O是△ABC的外接圆.
求:(1)⊙O的半径;
(2)BE的长.
20.如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°,BC=时,求⊙O的半径.
21.(1)如图(1),AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
(2)如图(2),⊙O是△ABC的外接圆,∠A=45°,BD是直径,且BD=2,连接CD,求BC的长.
22.如图,在平面直角坐标系内,已知点A(2,2),B(﹣6,﹣4),C(2,﹣4).
(1)求△ABC的外接圆的圆心点M的坐标;
(2)求△ABC的外接圆在x轴上所截弦DE的长.
参考答案
1.证明:∵点D在∠BAC的平分线上,
∴∠1=∠2.(1分)
又∵DE∥AC,
∴∠2=∠3,
∴∠1=∠3.(2分)
∴AE=DE.(3分)
又∵BD⊥AD于点D,
∴∠ADB=90°.(4分)
∴∠EBD+∠1=∠EDB+∠3=90°.(5分)
∴∠EBD=∠EDB.(6分)
∴BE=DE.(7分)
∴AE=BE=DE.(8分)
∴点E是A,B,D所在的圆的圆心.(10分)
2.证明:连接DB、DF,
∵∠A的平分线AD交圆于D,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,∠DFB=∠DFC=90°,∠BAD=∠CAD,
∴DB=DC,
∴在Rt△BED和Rt△CFD中,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF.
3.解:(1)△FBC是等边三角形,
∵∠CAM=120°,AD是∠CAM的平分线,
∴∠MAD=∠CAD=60°,
∵四边形AFBC是圆内接四边形,
∴∠FBC=∠CAD=60°,又∠BCF=∠FAB=∠MAD=60°,
∴△FBC是等边三角形;
(2)AB=AC+FA.
理由如下:在AB上截取AH=AC,
∵∠HAC=∠BFC=60°,
∴△AHC是等边三角形,
∴∠ACH=60°,CA=CH,
∵∠FCB=60°,
∴∠BCH=∠FCA,
在△BCH和△FCA中,
,
∴△BCH≌△FCA,
∴BH=FA,
∴AB=BH+AH=FA+AC.
4.解:(1)如图所示:分别作弦AB和AC的垂直平分线交点O即为所求的圆心;
(2)连接AO,OB,BC,BC交OA于D.
∵BC=16cm,
∴BD=8cm,
∵AB=10cm,
∴AD=6cm,
设圆片的半径为R,在Rt△BOD中,OD=(R﹣6)cm,
∴R2=82+(R﹣6)2,
解得:R=cm,
∴圆片的半径R为cm.
5.解:∵OO′=r==,O′P==2
同理可得:O′Q=1,O′R=,
∴O′P>r,点P在⊙O′外;
O′Q<r,点Q在⊙O′内;
O′R=r,点R在⊙O′上.
6.(1)证明:∵OD⊥BC,
∴BH=HC,
∵OA=OB,
∴AC=2OH.
(2)证明:∵OD⊥BC,
∴=,
∴∠BAD=∠DAC,
∵∠B=∠ADC,∠APB+∠BAD+∠B=180°,∠DAC+∠ACD+∠ADC=180°,
∴∠APB=∠ACD.
7.解:(1)根据垂径定理的推论:弦的垂直平分线必过圆心,
可以作弦AB和BC的垂直平分线,交点即为圆心.
如图所示,则圆心是(2,0)
故答案为:2,0.
(2)圆的半径AM==2,
线段MD==<2,
所以点D在⊙M内.
8.(1)证明:连BO并延长BO交AC于T.
∵AO=BO,
∴∠OAB=∠OBA,
又∵∠BAC+∠OAB=90°,
∴∠BAC+∠OBA=90°,
∴∠BTA=90°,
∴BT⊥AC,
∴=.
(2)延长AO并交⊙O于F,连接CF.
∵CD⊥AB于D,
∴∠CDA=90°,
∴∠OAB+∠AED=90°,
∵∠OAB+∠BAC=90°,
∴∠AED=∠BAC=∠FEC,
∵AF为⊙O直径,
∴∠ACF=90°,
同理:∠FCE=∠BAC,
∴∠FEC=∠FCE,
∴FE=FC,
∵AO=3,AE=4,
∴OE=1,FE=FC=2,
在Rt△FCA中
∴AC==4
9.解:(1)连接AP,
设AE=x,则(7﹣x)2+x2=25,
解得x=3或4
所以AE的长为3或4;
(2)当△APD是等腰直角三角形时,⊙A上满足条件的点P只有一个,
此时AD=AP=5
(3)观察图象可知:当5<a<5时,存在两个点P满足条件;
10.解:(1)∵∠AOB=90°,
∴AB是⊙M的直径,
∵A(8,0),B(0,6),
∴AB==10,
∴⊙M的半径为5,
由线段中点坐标公式x=,y=,得x=4,y=3,
∴M(4,3),
(2)点C在⊙M上,
理由:∵C(1,7),M(4,3),
∴CM==5,
∴点C在⊙M上.
11.(1)证明:如图1,
∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB;
(2)证明:由(1)得∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∵∠ABC=90°,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(3)解:由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
在Rt△ABC中,
∵AB=DH,
∴tan∠ACB==,
∴∠ACB=60°,
连接OD,
∵∠COD=23°,OD=OC,
∴∠OCD=(180°﹣23°)=()°,
∴∠PCB=180°﹣∠ACB﹣∠OCD=()°,
∵PC=PB,
∴∠P=180°﹣2×()°=97°.
12.解:如图,作直径AD,连接CD.
∴∠ACD=90°.
∵∠B=60°,
∴∠D=∠B=60°.
∵⊙O的半径为6,
∴AD=12.
在Rt△ACD中,∠CAD=30°,
∴CD=6.
∴AC=6.
13.证明:∵OD=OB,
∴∠ODB=∠OBD,
∵OD∥BC,
∴∠ODB=∠DBC,
∴∠DBC=∠OBD,
∴∠DAC=∠DCA,
∴AD=CD.
14.解:连接CD,
∵∠ABC=∠DAC,
∴=,
∴AC=CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∴AC=AD=6.
15.(1)证明:∵AB是⊙O的直径,
∴∠ADB=∠ADF=90°,
∵AD平分∠CAB,
∴∠FAD=∠BAD,
在△ADF和△ADB中,
,
∴△FAD≌△BAD,
∴AF=AB.
(2)连接OD,作OM⊥BD,则DM=BM,
∵OA=OB,
∴OM∥AD,AD=2OM,
∵AD平分∠CAB,
∴∠DAC=∠DAB,
∴=,
∴CD=BD,
∵OG平分CD,
∴OG⊥CD,DG=CG,
∴DG=DM,
在Rt△ODG和Rt△ODM中,
,
∴△ODG≌△ODM(HL),
∴OG=OM,
∴2OG=AD.
(3)∵CD为Rt△CBF斜边上的中线,
∴BF=2CD=2(4﹣2)=8﹣4,
设OA=r,则AF=AB=2r,AC=BC=r,
∴CF=(2﹣)r,
在Rt△BCF中,∵BC2+CF2=BF2,
∴(r)2+[(2﹣)r]2=(8﹣4)2,
∴r2=8﹣4,
∴⊙O的面积为(8﹣4)π.
16.(1)证明:∵AB是直径,∠ABC=30°,
∴∠ACB=90°,∠CAO=60°,
∵OA=OC,
∴△ACO是等边三角形,
∵CE=EO,
∴AE⊥CO,∠CAE=∠EAO=30°,
∵∠CDE=∠ABC=30°,
∴∠CDE=∠EAO,
在△CED和△OEA中,
,
∴△AEO≌△DEC.
(2)连接DO.
∵△AEO≌△DEC.∠CDE=∠EAO
∴CD=AO,CD∥AO,
∴四边形AODC是平行四边形,
∴S平行四边形AODC=2 S△ACO=2××62=18.
故答案为18.
17.解:(1)∵AF平分∠BAD,AE平分∠BAC,
∴∠BAF=∠BAD,∠BAE=∠BAC,
∴∠BAF+∠BAE=(∠BAD+∠BAC)=×180°=90°,即∠EAF=90°,
∴EF为⊙O的直径;
(2)∵AE平分∠BAC,
∴∠BAE=∠CAE,
∴=,
∴EF垂直平分BC.
18.解:(1)∵∠AOB=90°,
∴线段AB是⊙P的直径,
∵A(0,﹣6),B(8,0),PA=PB,
∴P(4,﹣3).
(2)∵=,
∴∠OAM=∠MAB,
∴AM是∠OAB的平分线.
19.解:(1)连接OB,
解方程x2﹣9x+18=0,
得,x1=3,x2=6,
由图形可知,AC=3,AB=6,
由圆周角定理得,∠AOB=2∠C=90°,
∴△AOB为等腰直角三角形,
∴OB=AB=3;
(2)∵∠C=45°,AE⊥BC,
∴△AEC为等腰直角三角形,
∴AE=AC=,
∴BE==.
20.(1)证明:∵OD⊥AC,
∴=,
∴∠CBD=∠DBA,
∴BD平分∠ABC;
(2)∵OD=OB,
∴∠OBD=∠ODB=30°,
∴∠ABC=60°,
∵AB是⊙O的直径,
∴∠ACB=90°,
在Rt△ABC中,∠A=30°,BC=,
∴AB=2BC=2,
∴⊙O的半径为.
21.证明:(1)∵∠1=∠2,
∴∠1+∠FBE=∠2+∠FBE,即∠ABE=∠CBF,
∵AB=CB,BE=BF,
∴△ABE≌△CBF(SAS);
(2)在圆O中,∵∠A=45°,=,
∴∠D=45°,
∵BD为圆的直径,
∴∠BCD=90°,
∴△BCD是等腰直角三角形,
∴BC=BD sin45°,
∵BD=2,
∴BC=.
22.解:(1)∵B(﹣6,﹣4),C(2,﹣4),
∴线段BC的垂直平分线是x=﹣2,
∵A(2,2),C(2,﹣4),
∴线段AC的垂直平分线是y=﹣1,
∴△ABC的外接圆的圆心M的坐标为:(﹣2,﹣1);
(2)连接OM,作MN⊥DE于N,
由题意得,AC=6,BC=8,
由勾股定理得,AB=10,
则DN==2,
由垂径定理得,DE=2DN=4.
