2021-2022学年北师大版九年级数学下册3.6直线与圆的位置关系 优生辅导训练(word版含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.6直线与圆的位置关系 优生辅导训练(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 523.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 09:42:01 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3.6直线与圆的位置关系》
优生辅导训练(附答案)
1.点P是半径为10的圆O所在平面上的一点,且点P到点O的距离为8.则过点P的直线l与圆O的位置关系为( )
A.相交 B.相切 C.相离 D.相交、相切、相离都有可能
2.在直角坐标平面内,已知点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为( )
A.0<r<5 B.3<r<5 C.4<r<5 D.3<r<4
3.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心作圆,如果圆A与线段BC没有公共点,那么圆A的半径r的取值范围是( )
A.5≥r≥3 B.3<r<5 C.r=3或r=5 D.0<r<3或r>5
4.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是( )
A.4<OC≤ B.4≤OC≤ C.4<OC D.4≤OC≤
5.如图,直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,横坐标为整数的点P的个数是( )
A.2 B.3 C.4 D.5
6.如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B.2 C. D.
7.如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
A.﹣1≤x≤1 B.﹣≤x≤ C.0<x≤ D.x>
8.在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点.对于一条直线,当它与一个圆的公共点都是整点时,我们把这条直线称为这个圆的“整点直线”.已知⊙O是以原点为圆心,半径为2的圆,则⊙O的“整点直线”共有( )条.
A.7 B.8 C.9 D.10
9.如图,已知直线y=,与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连接PA、PB,则△PAB面积的最小值是( )
A.6 B.5.5 C.5 D.4.5
10.如图,已知A、B两点的坐标分别为(0,﹣4)、(3,0),⊙C的圆心坐标为(0,1),半径为1,D是⊙C上的一动点,则△ABD面积的最大值为( )
A.9 B.12
C.20 D.10
11.已知在△ABC中,∠C=90°,AC=BC=2,如果以点C为圆心的圆与斜边AB有且只有一个交点,那么⊙C的半径是 .
12.动点A(m+2,3m+4)在直线l上,点B(b,0)在x轴上,如果以B为圆心,半径为1的圆与直线l有交点,则b的取值范围是 .
13.已知在直角坐标平面内,以点P(﹣2,3)为圆心,2为半径的圆P与x轴的位置关系是 .
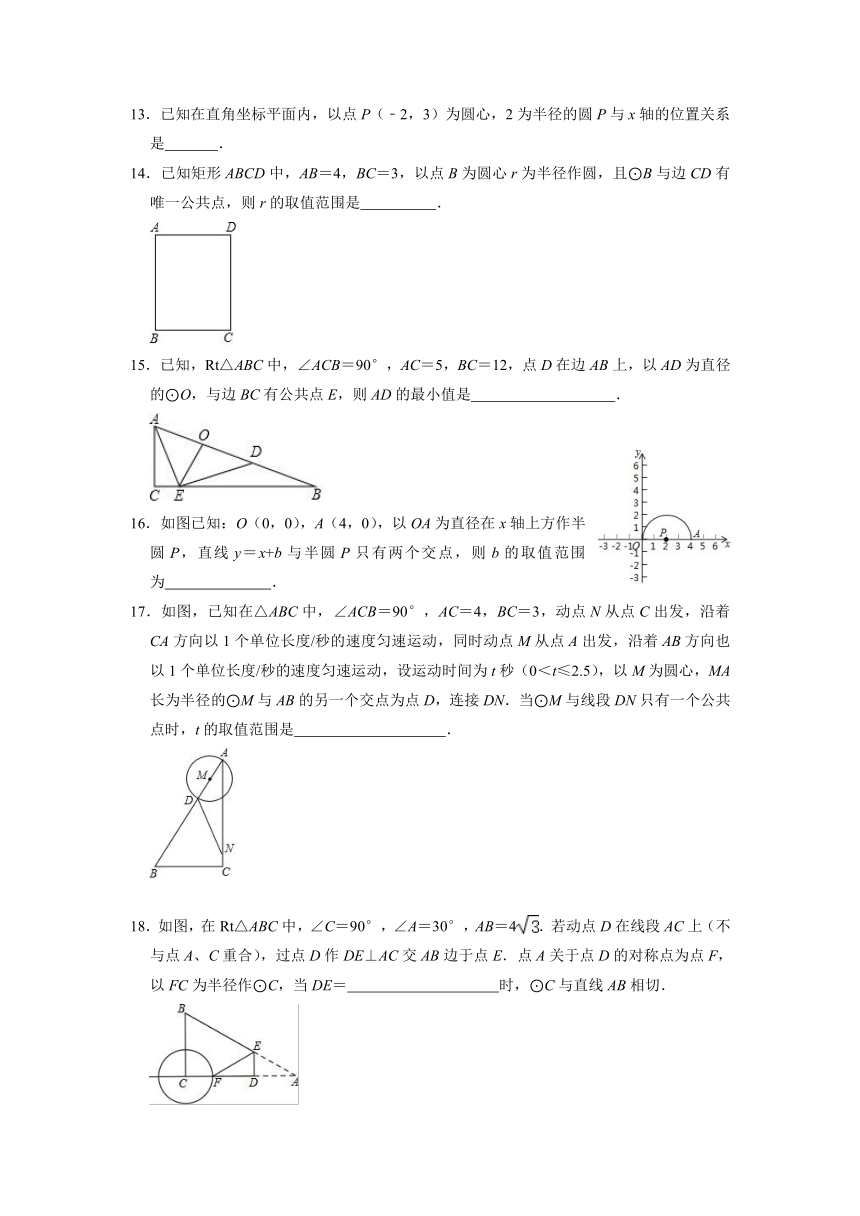
14.已知矩形ABCD中,AB=4,BC=3,以点B为圆心r为半径作圆,且⊙B与边CD有唯一公共点,则r的取值范围是 .
15.已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在边AB上,以AD为直径的⊙O,与边BC有公共点E,则AD的最小值是 .
16.如图已知:O(0,0),A(4,0),以OA为直径在x轴上方作半圆P,直线y=x+b与半圆P只有两个交点,则b的取值范围为 .
17.如图,已知在△ABC中,∠ACB=90°,AC=4,BC=3,动点N从点C出发,沿着CA方向以1个单位长度/秒的速度匀速运动,同时动点M从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤2.5),以M为圆心,MA长为半径的⊙M与AB的另一个交点为点D,连接DN.当⊙M与线段DN只有一个公共点时,t的取值范围是 .
18.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.
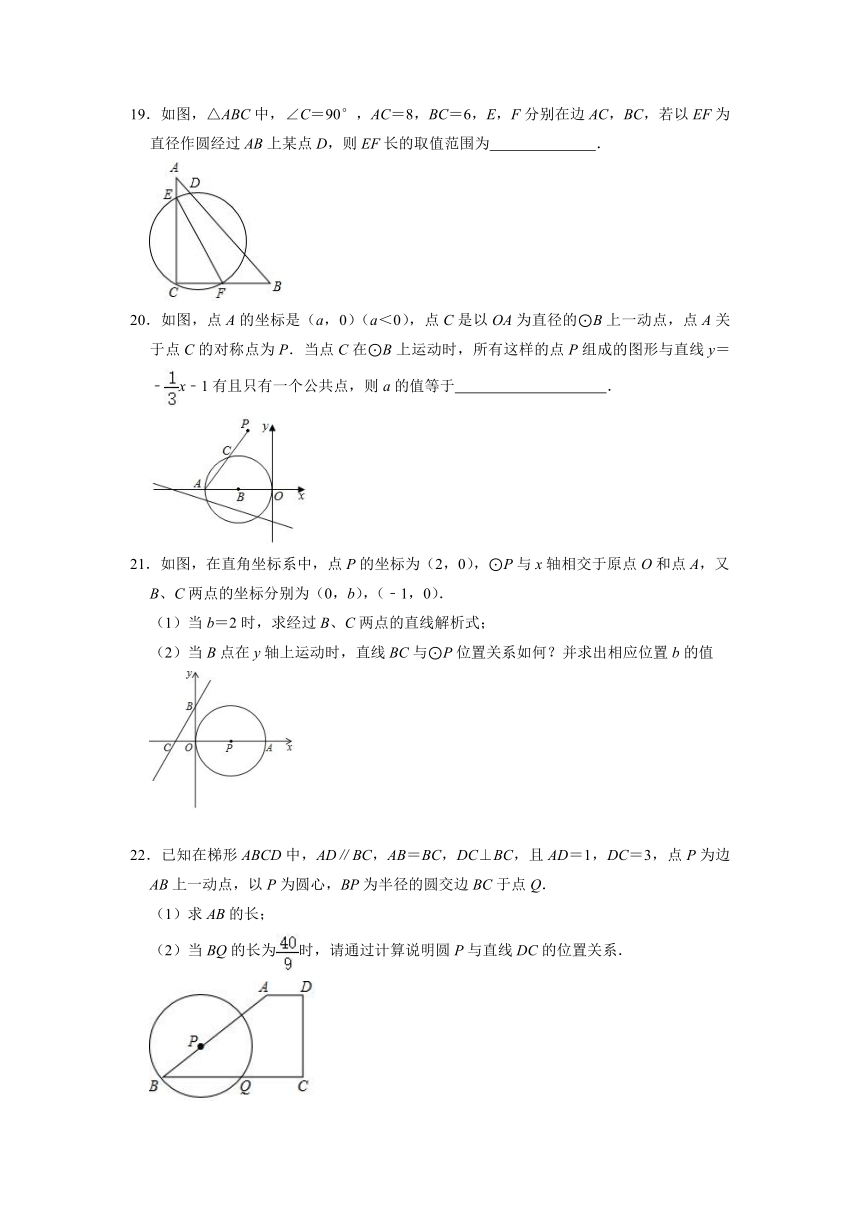
19.如图,△ABC中,∠C=90°,AC=8,BC=6,E,F分别在边AC,BC,若以EF为直径作圆经过AB上某点D,则EF长的取值范围为 .
20.如图,点A的坐标是(a,0)(a<0),点C是以OA为直径的⊙B上一动点,点A关于点C的对称点为P.当点C在⊙B上运动时,所有这样的点P组成的图形与直线y=﹣x﹣1有且只有一个公共点,则a的值等于 .
21.如图,在直角坐标系中,点P的坐标为(2,0),⊙P与x轴相交于原点O和点A,又B、C两点的坐标分别为(0,b),(﹣1,0).
(1)当b=2时,求经过B、C两点的直线解析式;
(2)当B点在y轴上运动时,直线BC与⊙P位置关系如何?并求出相应位置b的值
22.已知在梯形ABCD中,AD∥BC,AB=BC,DC⊥BC,且AD=1,DC=3,点P为边AB上一动点,以P为圆心,BP为半径的圆交边BC于点Q.
(1)求AB的长;
(2)当BQ的长为时,请通过计算说明圆P与直线DC的位置关系.
23.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径.动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q两点同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t,求:
(1)t分别为何值时,P、Q两点之间的距离是10cm?(四边形PQCD为平行四边形、等腰梯形?)
(2)t分别为何值时,直线PQ与⊙O相切、相离、相交?
24.如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以cm/s的速度,沿AC向C做匀速运动,与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB做匀速运动,当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts
(1)当P异于A,C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,⊙P与边BC公共点的个数有几种可能的情况?并求出相应的t所取的值.
参考答案
1.解:∵点P到点O的距离为8,圆O的半径为10,
∴8<10,
∴点P在圆内,
∴过点P的直线l与圆O的位置关系为相交,
故选:A.
2.解:∵点M的坐标是(4,3),
∴点M到x轴的距离是3,到y轴的距离是4,
∵点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,
∴r的取值范围是3<r<4,
故选:D.
3.解:∵在Rt△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心作圆,
当圆A的半径0<r<3或r>5时,圆A与线段BC没有公共点;
故选:D.
4.解:作DE⊥BC于E,如图所示:
则DE=AB=4,BE=AD=2,
∴CE=4=DE,
当⊙O与边AD相切时,切点为D,圆心O与E重合,即OC=4;
当OA=OC时,⊙O与AD交于点A,
设OA=OC=x,则OB=6﹣x,
在Rt△ABO中,由勾股定理得:42+(6﹣x)2=x2,
解得:x=;
∴以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是4≤x≤;
故选:B.
5.解:∵直线y=x+2与x轴、y轴分别相交于A,B两点,
圆心P的坐标为(1,0),
∴A点的坐标为:(﹣2,0),
B点的坐标为:(0,2),
∴AB=2,
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
根据△AP1C1∽△ABO,
∴==,
∴AP1=,
∴P1的坐标为:(﹣2+,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
根据△AP2C2∽△ABO,
∴==,
∴AP2=,
P2的坐标为:(﹣2﹣,0),
从﹣2﹣到﹣2+,整数点有﹣1,﹣2,﹣3,故横坐标为整数的点P的个数是,3个.
故选:B.
6.解:取DE的中点O,过O作OG⊥AB于G,连接OC,
又∵CO=1.5,
∴只有C、O、G三点一线时G到圆心O的距离最小,
∴此时OG达到最小.
∴MN达到最大.
作CF⊥AB于F,
∴G和F重合时,MN有最大值,
∵∠C=90°,BC=3,AC=4,
∴AB==5,
∵AC BC=AB CF,
∴CF=,
∴OG=﹣=,
∴MG==,
∴MN=2MG=,
故选:C.
7.解:∵半径为1的圆,∠AOB=45°,过点P且与OA平行的直线与⊙O有公共点,
∴当P′C与圆相切时,切点为C,
∴OC⊥P′C,
CO=1,∠P′OC=45°,OP′=,
∴过点P且与OA平行的直线与⊙O有公共点,即0<x≤,
同理点P在点O左侧时,0<x≤,
∴0<x≤.
故选:C.
8.解:∵圆的半径为2,
∴圆上的整数点有四个,(2,2),(2,﹣2),(﹣2,2),(﹣2,﹣2),
若直线与圆有两个交点,则两点确定一直线,可以画6条,
若直线与圆只有一个交点,则分别过这四个点画圆的切线,可以有4条,
∴一共有10条,
故选:D.
9.解:过C作CM⊥AB于M,连接AC,MC的延长线交⊙C于N,
则由三角形面积公式得,×AB×CM=×OA×BC,
∴5×CM=16,
∴CM=,
∴圆C上点到直线y=x﹣3的最小距离是 ﹣1=,
∴△PAB面积的最小值是 ×5×=,
故选:B.
10.解:如图,过点C作CE⊥AB,延长EC交⊙C于D,此时△ABD面积的最大值(AB是定值,只要圆上一点D到直线AB的距离最大),
设直线AB的解析式为y=kx+b(k≠0),
∵A(0,﹣4),B(3,0),
∴,
∴,
∴直线AB的解析式为y=x﹣4①,
∵CE⊥AB,C(0,1),
∴直线CE的解析式为y=﹣x+1②,
联立①②得,E(,﹣),
∵C(0,1),
∴CE==3,
∵⊙C的半径为1,
∴DE=CE+CD=3+1=4,
∵A(0,﹣4),B(3,0),
∴AB=5,
∴S△ABE面积的最大值=×5×4=10.
故选:D.
11.解:
∵在△ABC中,∠C=90°,AC=BC=2,
∵以点C为圆心的圆与斜边AB有且只有一个交点,
∴CD⊥AB,
∴CD=,
即⊙C的半径是
故答案为:.
12.解:∵动点A(m+2,3m+4)在直线l上,
∴直线l解析式为y=3x﹣2
如图,直线l与x轴交于点C(,0),交y轴于点E(0,﹣2)
∴OE=2,OC=
∴EC==
若以B为圆心,半径为1的圆与直线l相切于点D,连接BD
∴BD⊥AC
∴sin∠BCD=sin∠OCE=
∴
∴BC=
∴以B为圆心,半径为1的圆与直线l相切时,B点坐标为(﹣,0)或(+,0)
∴以B为圆心,半径为1的圆与直线l有交点,则b的取值范围是
故答案为:
13.解:∵点P的坐标为(﹣2,3),
∴点P到x轴的距离是3,
∵2<3,
∴以点P(﹣2,3)为圆心,2为半径的圆P与x轴的位置关系是相离,
故答案为:相离.
14.解:∵矩形ABCD中,AB=4,BC=3,
∴BD=AC==5,AD=BC=3,CD=AB=4,
∵以点B为圆心作圆,⊙B与边CD有唯一公共点,
∴⊙B的半径r的取值范围是:3≤r≤5;
故答案为:3≤r≤5
15.解:当E点是切点且EO⊥BC时,则AD有最小值,如图,
∵∠EBO=∠ABC,∠OEB=∠ACB=90°
∴△EBO∽△CBA,
∴,
∵Rt△ABC中,∠ACB=90°,AC=5,BC=12,
∴AB=13,
设OA=OD=OE=m,
∴
解得m=,
∴AD=2m=.
∴AD的最小值为=,
故答案为,
16.解:如图,当直线y=x+b与半圆相切于点E时,直线交x轴于F.
易知△PEF是等腰直角三角形,PE=EF=2,PF=2,
∴F(2﹣2,0),
∴0=2﹣2+b,
∴b=2﹣2,
当直线经过原点时,直线与半圆有两个交点,此时b=0,
观察图象可知满足条件的b的值为:0≤n<2﹣2.
故答案为:0≤b<2﹣2.
17.解:∵△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB===5,
分两种情况:
①当DN与⊙M相切时,则∠NDA=90°,
∵CN=AM=t,
∴AN=4﹣t,AD=2t,
∵∠A=∠A,∠NDA=∠ACB=90°,
∴△ADN∽△ACB,
∴=,即=,
∴t=;
∴当0<t≤时,⊙M与DN只有一个交点;
②当DN⊥AC时,则∠DNA=90°,
∵CN=AM=t,
∴AN=4﹣t,AD=2t,
∵∠A=∠A,∠DNA=∠ACB=90°,
∴△AND∽△ACB,
∴=,即=,
解得:t=,
∵0<t≤2.5,
∴<t≤;
综上所述,t的取值范围为0<t≤或<t≤;
故答案为:0<t≤或<t≤.
18.解:过C作CH⊥AB于H,
∵∠ACB=90°,BC=2,AB=4,AC=6,
∴由三角形面积公式得:BC AC=AB CH,
CH=3,
分为两种情况:①如图1,
∵CF=CH=3,
∴AF=6﹣3=3,
∵A和F关于D对称,
∴DF=AD=,
∵DE∥BC,
∴△ADE∽△ACB,
∴,
∴,
DE=
②如图2,∵CF=CH=3,
∴AF=6+3=9,
∵A和F关于D对称,
∴DF=AD=4.5,
∵DE∥BC,
∴△ADE∽△ACB,
∴,
∴,
DE=;
故答案为:或
19.解:∵∠C=90°,E,F分别在边AC,BC上,
∴△ECF是直角三角形,
∴点C在以EF为直径的圆上,
设以EF为直径的圆的圆心为O,
当⊙O于AB相切时,以EF为直径的圆经过AB上的唯一一点D,
连接CD,则CD⊥AB,且CD过圆心,
∴EF=CD,
∵∠C=90°,AC=8,BC=6,
∴AB=10,
∴EF=CD==4.8,
当⊙O经过A,B时,则EF=AB=10,
故EF长的取值范围为:4.8≤EF≤10.
故答案为:4.8≤EF≤10.
20.解:如图,连接BC,OP,设直线y=﹣x﹣1交x轴于点E(﹣3,0),交y轴于点F(0,﹣1),
∵AC=CP,AB=OB,
∴OP=2BC=﹣a,
∴点P的运动轨迹是以O为圆心﹣a为半径的圆,当⊙O与直线y=﹣x﹣1相切时,点P组成的图形与直线y=﹣x﹣1有且只有一个公共点,设切点为G,连接OG.
在Rt△EOF中,∵OG⊥EF,EF==, OE OF= EF OG,
∴OG=,
∴a=﹣,
故答案为:﹣.
21.解:(1)设BC直线的解析式:y=kx+b
由题意可得:
∴解得:k=2,b=2
∴BC的解析式为:y=2x+2
(2)设直线BC在x轴上方与⊙P相切于点M,交y轴于点D,连接PM,则PM⊥CM.
在Rt△CMP和Rt△COD中,
CP=3,MP=2,OC=1,CM=
∵∠MCP=∠OCD
∴tan∠MCP=tan∠OCD
∴=,b=OD=×1=
由轴对称性可知:b=±
∴当b=±时,直线BC与⊙P相切;
当b>或b<﹣时,直线BC与⊙P相离;
当﹣<b<时,直线BC与⊙P相交.
22.解:(1)过A作AE⊥BC于E,
则四边形AECD是矩形,
∴CE=AD=1,AE=CD=3,
∵AB=BC,
∴BE=AB﹣1,
在Rt△ABE中,∵AB2=AE2+BE2,
∴AB2=32+(AB﹣1)2,
解得:AB=5;
(2)过P作PF⊥BQ于F,
∴BF=BQ=,
∴△PBF∽△ABE,
∴=,
∴,
∴PB=,
∴PA=AB﹣PB=,
过P作PG⊥CD于G交AE于M,
∴GM=AD=1,PG∥BC,
∴△APM∽△ABE,
∴=,
∴=,
∴PM=,
∴PG=PM+MG==PB,
∴圆P与直线DC相切.
23.解:(1)AP=t,BQ=26﹣3t,如图1:作PE⊥BC于E,
QE=26﹣4t.
由勾股定理,得
(26﹣4t)2+64=100,
解得t=5或8;
(2)当PQ与⊙O相切时,如图2,
,
由相切,得PQ=AP+BQ=26﹣2t,
BE=26﹣4t,PE=8,
(26﹣4t)2+64=(26﹣2t)2
直线PQ与⊙O相切,t=8或;
当26÷3=,当t=时运动停止,
相交0≤t<或8<t≤;
相离<t<8.
24.解:(1)∵四边形ABCD是菱形,且菱形ABCD的边长为2cm,
∴AB=BC=2,∠BAC=∠DAB,
又∵∠DAB=60°(已知),
∴∠BAC=∠BCA=30°;
如图1,连接BD交AC于O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC,
∴OB=AB=1(30°角所对的直角边是斜边的一半),
∴OA=(cm),AC=2OA=2(cm),
运动ts后,AP=t,AQ=t,
∴==,
又∵∠PAQ=∠CAB,
∴△PAQ∽△CAB,
∴∠APQ=∠ACB(相似三角形的对应角相等),
∴PQ∥BC(同位角相等,两直线平行)
(2)如图2,⊙P与BC切于点M,连接PM,则PM⊥BC.
在Rt△CPM中,∵∠PCM=30°,
∴PM=PC=﹣t
由PM=PQ=AQ=t,即﹣t=t
解得t=4﹣6,此时⊙P与边BC有一个公共点;
∴当0≤t<4﹣6时,⊙P与边BC有0个公共点;
如图3,⊙P过点B,此时PQ=PB,
∵∠PQB=∠PAQ+∠APQ=60°
∴△PQB为等边三角形,∴QB=PQ=AQ=t,
∴t=1
∴当4﹣6<t≤1时,⊙P与边BC有2个公共点.
如图4,⊙P过点C,此时PC=PQ,即2﹣t=t,∴t=3﹣.
∴当1<t≤3﹣时,⊙P与边BC有一个公共点,当3﹣<t<2时,⊙P与边BC有0个公共点;
当点P运动到点C,即t=2时P与C重合,Q与B重合,也只有一个交点,此时,⊙P与边BC有一个公共点,
综上所述:当0≤t<4﹣6或3﹣<t<2时,⊙P与边BC有0个公共点;
当t=4﹣6或1<t≤3﹣或t=2时,⊙P与菱形ABCD的边BC有1个公共点;
当4﹣6<t≤1时,⊙P与边BC有2个公共点;
优生辅导训练(附答案)
1.点P是半径为10的圆O所在平面上的一点,且点P到点O的距离为8.则过点P的直线l与圆O的位置关系为( )
A.相交 B.相切 C.相离 D.相交、相切、相离都有可能
2.在直角坐标平面内,已知点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,那么r的取值范围为( )
A.0<r<5 B.3<r<5 C.4<r<5 D.3<r<4
3.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心作圆,如果圆A与线段BC没有公共点,那么圆A的半径r的取值范围是( )
A.5≥r≥3 B.3<r<5 C.r=3或r=5 D.0<r<3或r>5
4.如图,在梯形ABCD中,AD∥BC,∠B=90°,AD=2,AB=4,BC=6,点O是边BC上一点,以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是( )
A.4<OC≤ B.4≤OC≤ C.4<OC D.4≤OC≤
5.如图,直线y=x+2与x轴、y轴分别相交于A,B两点,圆心P的坐标为(1,0),圆P与y轴相切于点O.若将圆P沿x轴向左移动,当圆P与该直线相交时,横坐标为整数的点P的个数是( )
A.2 B.3 C.4 D.5
6.如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
A. B.2 C. D.
7.如图,已知⊙O圆心是数轴原点,半径为1,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
A.﹣1≤x≤1 B.﹣≤x≤ C.0<x≤ D.x>
8.在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点.对于一条直线,当它与一个圆的公共点都是整点时,我们把这条直线称为这个圆的“整点直线”.已知⊙O是以原点为圆心,半径为2的圆,则⊙O的“整点直线”共有( )条.
A.7 B.8 C.9 D.10
9.如图,已知直线y=,与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连接PA、PB,则△PAB面积的最小值是( )
A.6 B.5.5 C.5 D.4.5
10.如图,已知A、B两点的坐标分别为(0,﹣4)、(3,0),⊙C的圆心坐标为(0,1),半径为1,D是⊙C上的一动点,则△ABD面积的最大值为( )
A.9 B.12
C.20 D.10
11.已知在△ABC中,∠C=90°,AC=BC=2,如果以点C为圆心的圆与斜边AB有且只有一个交点,那么⊙C的半径是 .
12.动点A(m+2,3m+4)在直线l上,点B(b,0)在x轴上,如果以B为圆心,半径为1的圆与直线l有交点,则b的取值范围是 .
13.已知在直角坐标平面内,以点P(﹣2,3)为圆心,2为半径的圆P与x轴的位置关系是 .
14.已知矩形ABCD中,AB=4,BC=3,以点B为圆心r为半径作圆,且⊙B与边CD有唯一公共点,则r的取值范围是 .
15.已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在边AB上,以AD为直径的⊙O,与边BC有公共点E,则AD的最小值是 .
16.如图已知:O(0,0),A(4,0),以OA为直径在x轴上方作半圆P,直线y=x+b与半圆P只有两个交点,则b的取值范围为 .
17.如图,已知在△ABC中,∠ACB=90°,AC=4,BC=3,动点N从点C出发,沿着CA方向以1个单位长度/秒的速度匀速运动,同时动点M从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动,设运动时间为t秒(0<t≤2.5),以M为圆心,MA长为半径的⊙M与AB的另一个交点为点D,连接DN.当⊙M与线段DN只有一个公共点时,t的取值范围是 .
18.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4.若动点D在线段AC上(不与点A、C重合),过点D作DE⊥AC交AB边于点E.点A关于点D的对称点为点F,以FC为半径作⊙C,当DE= 时,⊙C与直线AB相切.
19.如图,△ABC中,∠C=90°,AC=8,BC=6,E,F分别在边AC,BC,若以EF为直径作圆经过AB上某点D,则EF长的取值范围为 .
20.如图,点A的坐标是(a,0)(a<0),点C是以OA为直径的⊙B上一动点,点A关于点C的对称点为P.当点C在⊙B上运动时,所有这样的点P组成的图形与直线y=﹣x﹣1有且只有一个公共点,则a的值等于 .
21.如图,在直角坐标系中,点P的坐标为(2,0),⊙P与x轴相交于原点O和点A,又B、C两点的坐标分别为(0,b),(﹣1,0).
(1)当b=2时,求经过B、C两点的直线解析式;
(2)当B点在y轴上运动时,直线BC与⊙P位置关系如何?并求出相应位置b的值
22.已知在梯形ABCD中,AD∥BC,AB=BC,DC⊥BC,且AD=1,DC=3,点P为边AB上一动点,以P为圆心,BP为半径的圆交边BC于点Q.
(1)求AB的长;
(2)当BQ的长为时,请通过计算说明圆P与直线DC的位置关系.
23.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB为⊙O的直径.动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q两点同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t,求:
(1)t分别为何值时,P、Q两点之间的距离是10cm?(四边形PQCD为平行四边形、等腰梯形?)
(2)t分别为何值时,直线PQ与⊙O相切、相离、相交?
24.如图,菱形ABCD的边长为2cm,∠DAB=60°.点P从A点出发,以cm/s的速度,沿AC向C做匀速运动,与此同时,点Q也从A点出发,以1cm/s的速度,沿射线AB做匀速运动,当P运动到C点时,P、Q都停止运动.设点P运动的时间为ts
(1)当P异于A,C时,请说明PQ∥BC;
(2)以P为圆心、PQ长为半径作圆,请问:在整个运动过程中,⊙P与边BC公共点的个数有几种可能的情况?并求出相应的t所取的值.
参考答案
1.解:∵点P到点O的距离为8,圆O的半径为10,
∴8<10,
∴点P在圆内,
∴过点P的直线l与圆O的位置关系为相交,
故选:A.
2.解:∵点M的坐标是(4,3),
∴点M到x轴的距离是3,到y轴的距离是4,
∵点M(4,3),以M为圆心,r为半径的圆与x轴相交,与y轴相离,
∴r的取值范围是3<r<4,
故选:D.
3.解:∵在Rt△ABC中,∠C=90°,AC=3,BC=4,以点A为圆心作圆,
当圆A的半径0<r<3或r>5时,圆A与线段BC没有公共点;
故选:D.
4.解:作DE⊥BC于E,如图所示:
则DE=AB=4,BE=AD=2,
∴CE=4=DE,
当⊙O与边AD相切时,切点为D,圆心O与E重合,即OC=4;
当OA=OC时,⊙O与AD交于点A,
设OA=OC=x,则OB=6﹣x,
在Rt△ABO中,由勾股定理得:42+(6﹣x)2=x2,
解得:x=;
∴以O为圆心,OC为半径的⊙O,与边AD只有一个公共点,则OC的取值范围是4≤x≤;
故选:B.
5.解:∵直线y=x+2与x轴、y轴分别相交于A,B两点,
圆心P的坐标为(1,0),
∴A点的坐标为:(﹣2,0),
B点的坐标为:(0,2),
∴AB=2,
将圆P沿x轴向左移动,当圆P与该直线相切于C1时,P1C1=1,
根据△AP1C1∽△ABO,
∴==,
∴AP1=,
∴P1的坐标为:(﹣2+,0),
将圆P沿x轴向左移动,当圆P与该直线相切于C2时,P2C2=1,
根据△AP2C2∽△ABO,
∴==,
∴AP2=,
P2的坐标为:(﹣2﹣,0),
从﹣2﹣到﹣2+,整数点有﹣1,﹣2,﹣3,故横坐标为整数的点P的个数是,3个.
故选:B.
6.解:取DE的中点O,过O作OG⊥AB于G,连接OC,
又∵CO=1.5,
∴只有C、O、G三点一线时G到圆心O的距离最小,
∴此时OG达到最小.
∴MN达到最大.
作CF⊥AB于F,
∴G和F重合时,MN有最大值,
∵∠C=90°,BC=3,AC=4,
∴AB==5,
∵AC BC=AB CF,
∴CF=,
∴OG=﹣=,
∴MG==,
∴MN=2MG=,
故选:C.
7.解:∵半径为1的圆,∠AOB=45°,过点P且与OA平行的直线与⊙O有公共点,
∴当P′C与圆相切时,切点为C,
∴OC⊥P′C,
CO=1,∠P′OC=45°,OP′=,
∴过点P且与OA平行的直线与⊙O有公共点,即0<x≤,
同理点P在点O左侧时,0<x≤,
∴0<x≤.
故选:C.
8.解:∵圆的半径为2,
∴圆上的整数点有四个,(2,2),(2,﹣2),(﹣2,2),(﹣2,﹣2),
若直线与圆有两个交点,则两点确定一直线,可以画6条,
若直线与圆只有一个交点,则分别过这四个点画圆的切线,可以有4条,
∴一共有10条,
故选:D.
9.解:过C作CM⊥AB于M,连接AC,MC的延长线交⊙C于N,
则由三角形面积公式得,×AB×CM=×OA×BC,
∴5×CM=16,
∴CM=,
∴圆C上点到直线y=x﹣3的最小距离是 ﹣1=,
∴△PAB面积的最小值是 ×5×=,
故选:B.
10.解:如图,过点C作CE⊥AB,延长EC交⊙C于D,此时△ABD面积的最大值(AB是定值,只要圆上一点D到直线AB的距离最大),
设直线AB的解析式为y=kx+b(k≠0),
∵A(0,﹣4),B(3,0),
∴,
∴,
∴直线AB的解析式为y=x﹣4①,
∵CE⊥AB,C(0,1),
∴直线CE的解析式为y=﹣x+1②,
联立①②得,E(,﹣),
∵C(0,1),
∴CE==3,
∵⊙C的半径为1,
∴DE=CE+CD=3+1=4,
∵A(0,﹣4),B(3,0),
∴AB=5,
∴S△ABE面积的最大值=×5×4=10.
故选:D.
11.解:
∵在△ABC中,∠C=90°,AC=BC=2,
∵以点C为圆心的圆与斜边AB有且只有一个交点,
∴CD⊥AB,
∴CD=,
即⊙C的半径是
故答案为:.
12.解:∵动点A(m+2,3m+4)在直线l上,
∴直线l解析式为y=3x﹣2
如图,直线l与x轴交于点C(,0),交y轴于点E(0,﹣2)
∴OE=2,OC=
∴EC==
若以B为圆心,半径为1的圆与直线l相切于点D,连接BD
∴BD⊥AC
∴sin∠BCD=sin∠OCE=
∴
∴BC=
∴以B为圆心,半径为1的圆与直线l相切时,B点坐标为(﹣,0)或(+,0)
∴以B为圆心,半径为1的圆与直线l有交点,则b的取值范围是
故答案为:
13.解:∵点P的坐标为(﹣2,3),
∴点P到x轴的距离是3,
∵2<3,
∴以点P(﹣2,3)为圆心,2为半径的圆P与x轴的位置关系是相离,
故答案为:相离.
14.解:∵矩形ABCD中,AB=4,BC=3,
∴BD=AC==5,AD=BC=3,CD=AB=4,
∵以点B为圆心作圆,⊙B与边CD有唯一公共点,
∴⊙B的半径r的取值范围是:3≤r≤5;
故答案为:3≤r≤5
15.解:当E点是切点且EO⊥BC时,则AD有最小值,如图,
∵∠EBO=∠ABC,∠OEB=∠ACB=90°
∴△EBO∽△CBA,
∴,
∵Rt△ABC中,∠ACB=90°,AC=5,BC=12,
∴AB=13,
设OA=OD=OE=m,
∴
解得m=,
∴AD=2m=.
∴AD的最小值为=,
故答案为,
16.解:如图,当直线y=x+b与半圆相切于点E时,直线交x轴于F.
易知△PEF是等腰直角三角形,PE=EF=2,PF=2,
∴F(2﹣2,0),
∴0=2﹣2+b,
∴b=2﹣2,
当直线经过原点时,直线与半圆有两个交点,此时b=0,
观察图象可知满足条件的b的值为:0≤n<2﹣2.
故答案为:0≤b<2﹣2.
17.解:∵△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB===5,
分两种情况:
①当DN与⊙M相切时,则∠NDA=90°,
∵CN=AM=t,
∴AN=4﹣t,AD=2t,
∵∠A=∠A,∠NDA=∠ACB=90°,
∴△ADN∽△ACB,
∴=,即=,
∴t=;
∴当0<t≤时,⊙M与DN只有一个交点;
②当DN⊥AC时,则∠DNA=90°,
∵CN=AM=t,
∴AN=4﹣t,AD=2t,
∵∠A=∠A,∠DNA=∠ACB=90°,
∴△AND∽△ACB,
∴=,即=,
解得:t=,
∵0<t≤2.5,
∴<t≤;
综上所述,t的取值范围为0<t≤或<t≤;
故答案为:0<t≤或<t≤.
18.解:过C作CH⊥AB于H,
∵∠ACB=90°,BC=2,AB=4,AC=6,
∴由三角形面积公式得:BC AC=AB CH,
CH=3,
分为两种情况:①如图1,
∵CF=CH=3,
∴AF=6﹣3=3,
∵A和F关于D对称,
∴DF=AD=,
∵DE∥BC,
∴△ADE∽△ACB,
∴,
∴,
DE=
②如图2,∵CF=CH=3,
∴AF=6+3=9,
∵A和F关于D对称,
∴DF=AD=4.5,
∵DE∥BC,
∴△ADE∽△ACB,
∴,
∴,
DE=;
故答案为:或
19.解:∵∠C=90°,E,F分别在边AC,BC上,
∴△ECF是直角三角形,
∴点C在以EF为直径的圆上,
设以EF为直径的圆的圆心为O,
当⊙O于AB相切时,以EF为直径的圆经过AB上的唯一一点D,
连接CD,则CD⊥AB,且CD过圆心,
∴EF=CD,
∵∠C=90°,AC=8,BC=6,
∴AB=10,
∴EF=CD==4.8,
当⊙O经过A,B时,则EF=AB=10,
故EF长的取值范围为:4.8≤EF≤10.
故答案为:4.8≤EF≤10.
20.解:如图,连接BC,OP,设直线y=﹣x﹣1交x轴于点E(﹣3,0),交y轴于点F(0,﹣1),
∵AC=CP,AB=OB,
∴OP=2BC=﹣a,
∴点P的运动轨迹是以O为圆心﹣a为半径的圆,当⊙O与直线y=﹣x﹣1相切时,点P组成的图形与直线y=﹣x﹣1有且只有一个公共点,设切点为G,连接OG.
在Rt△EOF中,∵OG⊥EF,EF==, OE OF= EF OG,
∴OG=,
∴a=﹣,
故答案为:﹣.
21.解:(1)设BC直线的解析式:y=kx+b
由题意可得:
∴解得:k=2,b=2
∴BC的解析式为:y=2x+2
(2)设直线BC在x轴上方与⊙P相切于点M,交y轴于点D,连接PM,则PM⊥CM.
在Rt△CMP和Rt△COD中,
CP=3,MP=2,OC=1,CM=
∵∠MCP=∠OCD
∴tan∠MCP=tan∠OCD
∴=,b=OD=×1=
由轴对称性可知:b=±
∴当b=±时,直线BC与⊙P相切;
当b>或b<﹣时,直线BC与⊙P相离;
当﹣<b<时,直线BC与⊙P相交.
22.解:(1)过A作AE⊥BC于E,
则四边形AECD是矩形,
∴CE=AD=1,AE=CD=3,
∵AB=BC,
∴BE=AB﹣1,
在Rt△ABE中,∵AB2=AE2+BE2,
∴AB2=32+(AB﹣1)2,
解得:AB=5;
(2)过P作PF⊥BQ于F,
∴BF=BQ=,
∴△PBF∽△ABE,
∴=,
∴,
∴PB=,
∴PA=AB﹣PB=,
过P作PG⊥CD于G交AE于M,
∴GM=AD=1,PG∥BC,
∴△APM∽△ABE,
∴=,
∴=,
∴PM=,
∴PG=PM+MG==PB,
∴圆P与直线DC相切.
23.解:(1)AP=t,BQ=26﹣3t,如图1:作PE⊥BC于E,
QE=26﹣4t.
由勾股定理,得
(26﹣4t)2+64=100,
解得t=5或8;
(2)当PQ与⊙O相切时,如图2,
,
由相切,得PQ=AP+BQ=26﹣2t,
BE=26﹣4t,PE=8,
(26﹣4t)2+64=(26﹣2t)2
直线PQ与⊙O相切,t=8或;
当26÷3=,当t=时运动停止,
相交0≤t<或8<t≤;
相离<t<8.
24.解:(1)∵四边形ABCD是菱形,且菱形ABCD的边长为2cm,
∴AB=BC=2,∠BAC=∠DAB,
又∵∠DAB=60°(已知),
∴∠BAC=∠BCA=30°;
如图1,连接BD交AC于O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=AC,
∴OB=AB=1(30°角所对的直角边是斜边的一半),
∴OA=(cm),AC=2OA=2(cm),
运动ts后,AP=t,AQ=t,
∴==,
又∵∠PAQ=∠CAB,
∴△PAQ∽△CAB,
∴∠APQ=∠ACB(相似三角形的对应角相等),
∴PQ∥BC(同位角相等,两直线平行)
(2)如图2,⊙P与BC切于点M,连接PM,则PM⊥BC.
在Rt△CPM中,∵∠PCM=30°,
∴PM=PC=﹣t
由PM=PQ=AQ=t,即﹣t=t
解得t=4﹣6,此时⊙P与边BC有一个公共点;
∴当0≤t<4﹣6时,⊙P与边BC有0个公共点;
如图3,⊙P过点B,此时PQ=PB,
∵∠PQB=∠PAQ+∠APQ=60°
∴△PQB为等边三角形,∴QB=PQ=AQ=t,
∴t=1
∴当4﹣6<t≤1时,⊙P与边BC有2个公共点.
如图4,⊙P过点C,此时PC=PQ,即2﹣t=t,∴t=3﹣.
∴当1<t≤3﹣时,⊙P与边BC有一个公共点,当3﹣<t<2时,⊙P与边BC有0个公共点;
当点P运动到点C,即t=2时P与C重合,Q与B重合,也只有一个交点,此时,⊙P与边BC有一个公共点,
综上所述:当0≤t<4﹣6或3﹣<t<2时,⊙P与边BC有0个公共点;
当t=4﹣6或1<t≤3﹣或t=2时,⊙P与菱形ABCD的边BC有1个公共点;
当4﹣6<t≤1时,⊙P与边BC有2个公共点;
