2021-2022学年北师大版九年级数学下册3.8圆内接正多边形选择题专题训练(word解析版)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.8圆内接正多边形选择题专题训练(word解析版) | 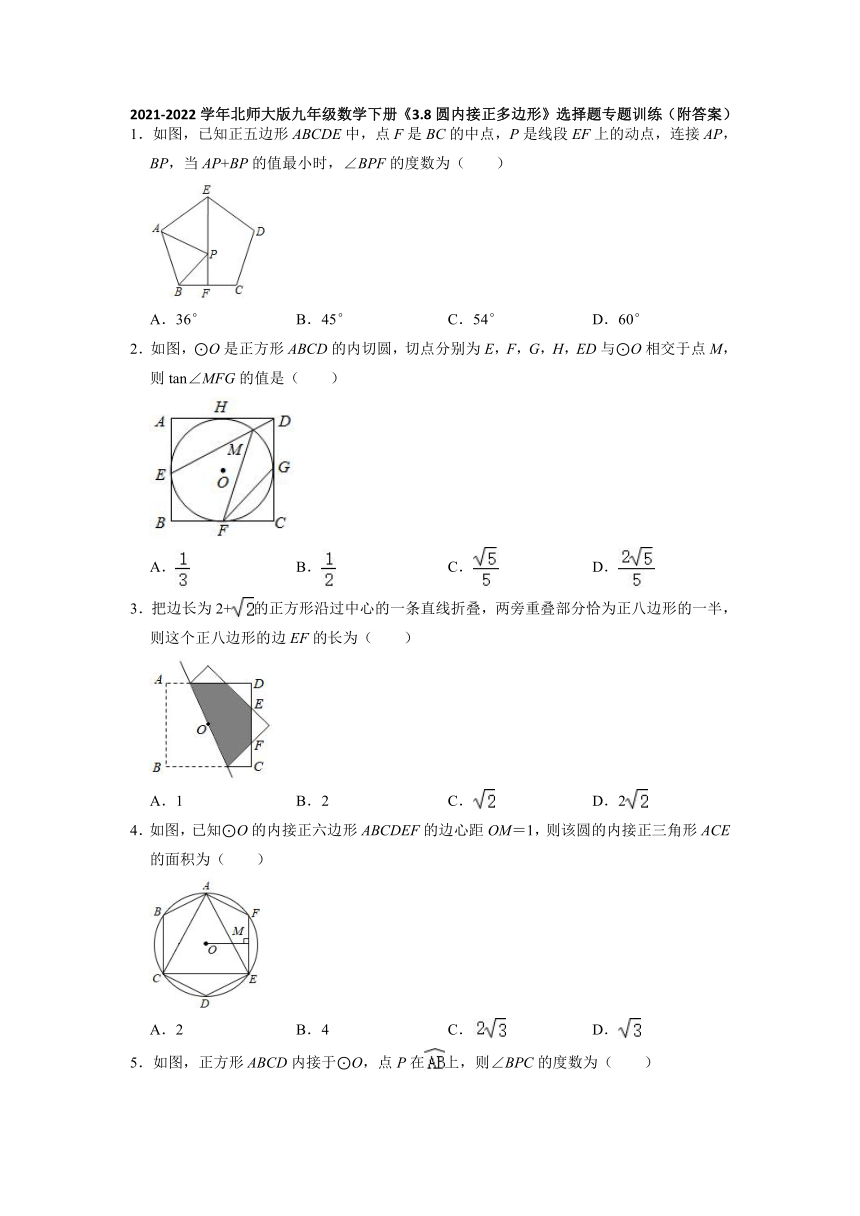 | |
| 格式 | doc | ||
| 文件大小 | 461.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 11:17:12 | ||
图片预览





文档简介
2021-2022学年北师大版九年级数学下册《3.8圆内接正多边形》选择题专题训练(附答案)
1.如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为( )
A.36° B.45° C.54° D.60°
2.如图,⊙O是正方形ABCD的内切圆,切点分别为E,F,G,H,ED与⊙O相交于点M,则tan∠MFG的值是( )
A. B. C. D.
3.把边长为2+的正方形沿过中心的一条直线折叠,两旁重叠部分恰为正八边形的一半,则这个正八边形的边EF的长为( )
A.1 B.2 C. D.2
4.如图,已知⊙O的内接正六边形ABCDEF的边心距OM=1,则该圆的内接正三角形ACE的面积为( )
A.2 B.4 C. D.
5.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
6.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于( )
A.72° B.54° C.36° D.64°
7.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
8.如图,已知正六边形ABCDEF的边长为1,分别以其对角线AD、CE为边作正方形,则两个阴影部分的面积差a﹣b的值为( )
A.0 B.2 C.1 D.
9.如图,在正五边形ABCDE中,连接AC,BE,BD,AC与BE,BD分别交于点F,G,若AB=2,则FG的长为( )
A.3﹣ B.﹣1 C. D.2﹣3
10.如图,若⊙O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2:3 B.:1 C.: D.1:
嘉淇用一些完全相同的△ABC纸片拼接图案,已知用六个△ABC纸片按照图1所示的方法拼接可得外轮廓是正六边形图案,若用n个△ABC纸片按图2所示的方法拼接,那么可以得到外轮廓的图案是( )
A.正十二边形 B.正十边形 C.正九边形 D.正八边形
12.如图,在2×2的网格中,每个小正方形的边长均为1,A,B,C,E为格点.⊙O为大正方形的内切圆,BC交⊙O于点D,则cos∠AED=( )
A. B. C. D.
13.正多边形的内切圆与外接圆的半径之比为,则这个正多边形为( )
A.正十二边形 B.正六边形 C.正四边形 D.正三角形
14.如图,两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上,点P在上,则tan∠API的值是( )
A.2 B.2 C.2 D.1
15.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,点M为劣弧FG的中点.若FM=2,则⊙O的半径为( )
A.2 B. C.2 D.2
16.如图,将边长为6的正六边形ABCDEF沿HG折叠,点B的对应点B′恰好落在边AF的中点上,点C、D的对应点为C′、D′,延长B′C′交EF于点M,则C′M的长为( )
A.1 B. C. D.
17.如图,在正五边形ABCDE中,连接AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是( )
A.18° B.30° C.36° D.40°
18.如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环共需( )个五边形.
A.7 B.8 C.9 D.10
19.如图,是圆的内接n边形.M,N分别从B,C开始以相同的速度在⊙O上逆时针运动,则∠APN的度数和正多边形边数n的关系是( )
A. B. C. D.
20.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为( )
A. B. C. D.2
21.如图,六边形ABCDEF是正六边形,点P是边AF的中点,PC,PD分别与BE交于点M,N,则S△PBM:S四边形MCDN的值为( )
A. B. C. D.
22.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是( )
A.18° B.36° C.54° D.72°
23.如图,正五边形ABCDE与正三角形AMN都是⊙O的内接多边形,若连接BM,则∠MBC的度数是( )
A.12° B.15° C.30° D.48°
24.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A.3 B. C.2 D.
25.如图,设ABCDE是正五边形,五角星ACEBD(阴影部分)的面积为1,设AC与BE的交点为P,BD与CE交点为Q,则四边形APQD的面积等于( )
A. B. C. D.
参考答案
1.解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PB,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣∠P′BC=90°﹣36°=54°.
故选:C.
2.解:连接EG,
∵EG是切点,
∴EG过⊙O,
∵⊙O是正方形ABCD的内切圆,
∴AE=AB,EG=BC,
根据圆周角的性质可得:∠MFG=∠MEG.
∵tan∠MFG=tan∠MEG==.
故选:B.
3.解:如图,
∵重叠部分为正八边形的一半,
∴GF=EF=PE=HP,∠GFE=∠FEP=∠HPE=135°,
∴∠GFC=∠B'FE=∠DEP=∠A'PH=45°,
∴△CGF、△B'EF是全等的等腰直角三角形,
设CG=x,则GF=x,B'F=x,
∴BG=B'G=x+x,
∴BC=x+x+x=2+,
∴x=1,
∴GF=,
故选:C.
4.解:如图所示,连接OE、OF,过O作ON⊥CE于N,
∵多边形ABCDEF是正六边形,
∴∠EOF=60°,
∵OE=OF,
∴△EOF是等边三角形,
∴∠OEM=60°,
∴OM=OE sin∠OEM,
∴OE==,
∵∠OEN=30°,
∴ON=OE=,EN=1.
∴CE=2EN=2.
∴S△ACE=.
故选:D.
5.解:连接OB、OC,如图,
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
故选:B.
6.解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣36°=54°,
故选:B.
7.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
8.解:∵正六边形ABCDEF的边长为1,
∴AD=2,EC=,
∴AD为边的正方形的面积为4,EC为边的正方形的面积为3,
∵a+空白=4,b+空白=3,
∴两个阴影部分的面积差a﹣b=4﹣3=1,
故选:C.
9.解:∵五边形ABCDE是正五边形,
∴∠BAF=∠ABF=∠DBE=36°,
∴FA=FB,
∴∠ABG=∠AGB=∠BFG=72°,
∴AB=AG=2,BG=BF,
设AF=BF=BG=x,
∵∠BGF=∠AGB,∠GBF=∠GAB,
∴△BGF∽△AGB,
∴BG2=GF GA,
∴x2=(2﹣x)×2,
∴x2+2x﹣4=0,
∴x=﹣1+或﹣1﹣(舍弃),
∴FG=AG﹣AF=2﹣(﹣1+)=3﹣,
故选:A.
10.解:连接OA、OB.OE,如图所示:
设此圆的半径为R,
则它的内接正方形的边长为R,它的内接正六边形的边长为R,
∴内接正方形和内接正六边形的边长之比为R:R=:1,
∴正方形ABCD与正六边形AEFCGH的周长之比=内接正方形和内接正六边形的边长之比=4:6=2:3,
故选:A.
11.解:∵正六边形每一个内角为120°,
∴∠ACB=120°﹣80°=40°,
∴∠CAB=180°﹣120°=60°,
∴图2中正多边形的每一个内角为60°+80°=140°,
∵=9,
∴可以得到外轮廓的图案是正九边形.
故选:C.
12.解:在Rt△ABC中,AC=1,AB=2,
∴BC===,
∴cos∠ABC===,
∵∠AED=∠ABC,
∴cos∠AED=cos∠ABC=,
故选:B.
13.解:如图,设AB是正多边形的一边,O为正多边形的内切圆与外接圆的圆心,OC⊥AB于C,
∵正多边形的内切圆与外接圆的半径之比为,
∴=,
在Rt△AOC中,cos∠AOC==,
∴∠AOC=45°,
∴∠AOB=2∠AOC=90°,
则正多边形边数为:=4.
故选:C.
14.解:如图,连接AE,EI,AH,过点J作JM⊥EI于M.
∵ABCDEF是正六边形,
∴∠DEF=∠F=120°,
∵FA=FE,
∴∠FEA=∠FAE=30°,
∴∠AED=90°,
同法可证,∠DEI=∠EIH=90°,
∴∠AED+∠DEI=180°,
∴A,E,I共线,
设IH=IJ=JE=a,
∵JM⊥EI,
∴EM=MI=a,
∴AI=2EI=2a,
∵∠API=∠AHI,
∴tan∠API=tan∠AHI===2,
故选:A.
15.解:如图,连接OM,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,OM=OF,
∴△OFM是等边三角形,
∴OM=OF=FM=2.
则⊙O的半径为2.
故选:C.
16.解:如图,过点H作FA的延长线的垂线HQ,
∵∠BAF=120°,
∴∠HAQ=60°,∠HQA=90°,
∴∠AHQ=30°,
设AH=x,∴AQ=x,QH=x,
∴BH=B′H=AB﹣AH=6﹣x,
∵AB′=AB=3,
∴B′Q=B′A+AQ=3+x,
在Rt△B′HQ中,根据勾股定理,得
B′H2=B′Q2+QH2,
∴(6﹣x)2=(3+x)2+x2,
解得x=,
∴B′H=6﹣x==,
∵∠HAB′=∠F=∠HB′M=120°,
∴∠AHB′+∠AB′H=60°,∠FB′M+∠AB′H=60°,
∴∠AHB′=∠FB′M,
∴△AB′M∽△FMB′,
∴=,
∴=,
解得B′M=7,
∴C′M=B′M﹣B′C′=7﹣6=1.
故选:A.
17.解:∵五边形ABCDE是正五边形,
∴∠AED=∠EAB=∠ABC=108°,
∵BA=BC,
∴∠BAC=∠BCA=36°,
∴∠EAC=72°,
∴∠AED+∠EAC=180°,
∴DE∥AF,
∵AE=AF=DE,
∴四边形AEDF是菱形,
∴∠EDF=∠EAF=72°,
∵∠EDC=108°,
∴∠FDC=36°,
故选:C.
18.解:延长正五边形的相邻两边,交于圆心,
∵正五边形的外角等于360°÷5=72°,
∴延长正五边形的相邻两边围成的角的度数为:180°﹣72°﹣72°=36°,
∴360°÷36°=10,
∴排成圆环需要10个正五边形,
故选:D.
19.解:∵点M、N以相同的速度中⊙O上逆时针运动,
∴=,
∴∠BAM=∠NBC,
∴∠APN=∠ABP+∠NBC,
∵∠APN=∠ABP+∠BAM=∠ABP+∠CBN=∠ABC,
∴∠APN的度数等于多边形的内角的度数,
当正多边形为n边形时,其内角和为(n﹣2)180°,
∵每个内角的度数为,
∴∠APN=,
故选:B.
20.解:如图,连接AC、BD、OF,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=r sin60°=r,
∴EF=r×2=r,
∵AO=2OI,
∴OI=r,CI=r﹣r=r,
∴==,
∴GH=BD=r,
∴==.
故选:C.
21.解:设正六边形的边长为a.则S△PCD=2×a2=a2,S四边形BCDE=3×a2=a2,
由题意MN是△PCD的中位线,
∴S△PMN=S△PCD=a2,
∴S四边形MNDC=a2﹣a2=a2,
∴S△BMC=S△DNE=(a2﹣a2)=a2,
∵PM=CM,
∴S△PBM=S△BMC=a2,
∴S△PBM:S四边形MCDN=a2:a2=1:2,
故选:A.
22.解:∵AF是⊙O的直径,五边形ABCDE是⊙O的内接正五边形,
∴,,∠BAE=108°,
∴,
∴∠BAF=∠BAE=54°,
∴∠BDF=∠BAF=54°,
故选:C.
23.解:连接OA、OC.
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∴∠AOC=72°×2=144°,
∵△AMN是正三角形,
∴∠AOM==120°,
∴∠COM=∠AOC﹣∠AOM=144°﹣120°=24°,
∴∠MBC=∠COM=×24°=12°.
故选:A.
24.解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD=a.
∴BH=DB+DH=(+1)a.
在Rt△ABH中,tan∠HAB==+1.
故选:B.
25.解:设AD与BE交于点R,AC与BD交于点H,AD与CE交于点J,连接RQ,如图所示:
∵由五角星的性质可知:△APR≌△BHP≌△CQH≌△DJQ≌△ERJ,AP=AR,JR=JQ=HQ=HP,AR=CQ,
∴RQ∥AC,
同理:PQ∥AD,
∴四边形APQR为平行四边形,
∵AP=AR,
∴四边形APQR为菱形,
∴△APR与△PQR面积相等,PQ=RQ,
在△HPQ和△JRQ中,,
∴△HPQ≌△JRQ(SSS),
∴△HPQ和△JRQ的面积相等,
设△APR的面积为S1,△HPQ的面积为S2,
则1=6S1+2S2,
∴SAPQD=3S1+S2=,
故选:D.
1.如图,已知正五边形ABCDE中,点F是BC的中点,P是线段EF上的动点,连接AP,BP,当AP+BP的值最小时,∠BPF的度数为( )
A.36° B.45° C.54° D.60°
2.如图,⊙O是正方形ABCD的内切圆,切点分别为E,F,G,H,ED与⊙O相交于点M,则tan∠MFG的值是( )
A. B. C. D.
3.把边长为2+的正方形沿过中心的一条直线折叠,两旁重叠部分恰为正八边形的一半,则这个正八边形的边EF的长为( )
A.1 B.2 C. D.2
4.如图,已知⊙O的内接正六边形ABCDEF的边心距OM=1,则该圆的内接正三角形ACE的面积为( )
A.2 B.4 C. D.
5.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
6.如图,正五边形ABCDE内接于⊙O,点P为上一点(点P与点D,点E不重合),连接PC,PD,DG⊥PC,垂足为G,则∠PDG等于( )
A.72° B.54° C.36° D.64°
7.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A. B. C. D.
8.如图,已知正六边形ABCDEF的边长为1,分别以其对角线AD、CE为边作正方形,则两个阴影部分的面积差a﹣b的值为( )
A.0 B.2 C.1 D.
9.如图,在正五边形ABCDE中,连接AC,BE,BD,AC与BE,BD分别交于点F,G,若AB=2,则FG的长为( )
A.3﹣ B.﹣1 C. D.2﹣3
10.如图,若⊙O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2:3 B.:1 C.: D.1:
嘉淇用一些完全相同的△ABC纸片拼接图案,已知用六个△ABC纸片按照图1所示的方法拼接可得外轮廓是正六边形图案,若用n个△ABC纸片按图2所示的方法拼接,那么可以得到外轮廓的图案是( )
A.正十二边形 B.正十边形 C.正九边形 D.正八边形
12.如图,在2×2的网格中,每个小正方形的边长均为1,A,B,C,E为格点.⊙O为大正方形的内切圆,BC交⊙O于点D,则cos∠AED=( )
A. B. C. D.
13.正多边形的内切圆与外接圆的半径之比为,则这个正多边形为( )
A.正十二边形 B.正六边形 C.正四边形 D.正三角形
14.如图,两个正六边形ABCDEF、EDGHIJ的顶点A、B、H、I在同一个圆上,点P在上,则tan∠API的值是( )
A.2 B.2 C.2 D.1
15.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,点M为劣弧FG的中点.若FM=2,则⊙O的半径为( )
A.2 B. C.2 D.2
16.如图,将边长为6的正六边形ABCDEF沿HG折叠,点B的对应点B′恰好落在边AF的中点上,点C、D的对应点为C′、D′,延长B′C′交EF于点M,则C′M的长为( )
A.1 B. C. D.
17.如图,在正五边形ABCDE中,连接AC,以点A为圆心,AB为半径画圆弧交AC于点F,连接DF.则∠FDC的度数是( )
A.18° B.30° C.36° D.40°
18.如图,若干全等正五边形排成环状.图中所示的是前3个五边形,要完成这一圆环共需( )个五边形.
A.7 B.8 C.9 D.10
19.如图,是圆的内接n边形.M,N分别从B,C开始以相同的速度在⊙O上逆时针运动,则∠APN的度数和正多边形边数n的关系是( )
A. B. C. D.
20.如图,正方形ABCD和正三角形AEF都内接于⊙O,EF与BC,CD分别相交于点G,H,则的值为( )
A. B. C. D.2
21.如图,六边形ABCDEF是正六边形,点P是边AF的中点,PC,PD分别与BE交于点M,N,则S△PBM:S四边形MCDN的值为( )
A. B. C. D.
22.如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是( )
A.18° B.36° C.54° D.72°
23.如图,正五边形ABCDE与正三角形AMN都是⊙O的内接多边形,若连接BM,则∠MBC的度数是( )
A.12° B.15° C.30° D.48°
24.如图,在正六边形ABCDEF外作正方形DEGH,连接AH,则tan∠HAB等于( )
A.3 B. C.2 D.
25.如图,设ABCDE是正五边形,五角星ACEBD(阴影部分)的面积为1,设AC与BE的交点为P,BD与CE交点为Q,则四边形APQD的面积等于( )
A. B. C. D.
参考答案
1.解:如图,连接AC,PC,设AC交EF于点P′,连接BP′.
∵正五边形ABCDE中,点F是BC的中点,
∵EF⊥BC,
∴B,C关于EF对称,
∴PB=PB,
∵PA+PB=PA+PC≥AC,
∴当点P与P′重合时,PA+PB的值最小,
∵ABCDE是正五边形,
∴BA=BC,∠ABC=108°,
∴∠BAC=∠BCA=36°,
∵P′B=CP′,
∴∠P′BC=∠P′CB=36°,
∵∠EFB=90°,
∴∠BP′F=90°﹣∠P′BC=90°﹣36°=54°.
故选:C.
2.解:连接EG,
∵EG是切点,
∴EG过⊙O,
∵⊙O是正方形ABCD的内切圆,
∴AE=AB,EG=BC,
根据圆周角的性质可得:∠MFG=∠MEG.
∵tan∠MFG=tan∠MEG==.
故选:B.
3.解:如图,
∵重叠部分为正八边形的一半,
∴GF=EF=PE=HP,∠GFE=∠FEP=∠HPE=135°,
∴∠GFC=∠B'FE=∠DEP=∠A'PH=45°,
∴△CGF、△B'EF是全等的等腰直角三角形,
设CG=x,则GF=x,B'F=x,
∴BG=B'G=x+x,
∴BC=x+x+x=2+,
∴x=1,
∴GF=,
故选:C.
4.解:如图所示,连接OE、OF,过O作ON⊥CE于N,
∵多边形ABCDEF是正六边形,
∴∠EOF=60°,
∵OE=OF,
∴△EOF是等边三角形,
∴∠OEM=60°,
∴OM=OE sin∠OEM,
∴OE==,
∵∠OEN=30°,
∴ON=OE=,EN=1.
∴CE=2EN=2.
∴S△ACE=.
故选:D.
5.解:连接OB、OC,如图,
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC=∠BOC=45°.
故选:B.
6.解:连接OC,OD.
在正五边形ABCDE中,∠COD==72°,
∴∠CPD=∠COD=36°,
∵DG⊥PC,
∴∠PGD=90°,
∴∠PDG=90°﹣36°=54°,
故选:B.
7.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
8.解:∵正六边形ABCDEF的边长为1,
∴AD=2,EC=,
∴AD为边的正方形的面积为4,EC为边的正方形的面积为3,
∵a+空白=4,b+空白=3,
∴两个阴影部分的面积差a﹣b=4﹣3=1,
故选:C.
9.解:∵五边形ABCDE是正五边形,
∴∠BAF=∠ABF=∠DBE=36°,
∴FA=FB,
∴∠ABG=∠AGB=∠BFG=72°,
∴AB=AG=2,BG=BF,
设AF=BF=BG=x,
∵∠BGF=∠AGB,∠GBF=∠GAB,
∴△BGF∽△AGB,
∴BG2=GF GA,
∴x2=(2﹣x)×2,
∴x2+2x﹣4=0,
∴x=﹣1+或﹣1﹣(舍弃),
∴FG=AG﹣AF=2﹣(﹣1+)=3﹣,
故选:A.
10.解:连接OA、OB.OE,如图所示:
设此圆的半径为R,
则它的内接正方形的边长为R,它的内接正六边形的边长为R,
∴内接正方形和内接正六边形的边长之比为R:R=:1,
∴正方形ABCD与正六边形AEFCGH的周长之比=内接正方形和内接正六边形的边长之比=4:6=2:3,
故选:A.
11.解:∵正六边形每一个内角为120°,
∴∠ACB=120°﹣80°=40°,
∴∠CAB=180°﹣120°=60°,
∴图2中正多边形的每一个内角为60°+80°=140°,
∵=9,
∴可以得到外轮廓的图案是正九边形.
故选:C.
12.解:在Rt△ABC中,AC=1,AB=2,
∴BC===,
∴cos∠ABC===,
∵∠AED=∠ABC,
∴cos∠AED=cos∠ABC=,
故选:B.
13.解:如图,设AB是正多边形的一边,O为正多边形的内切圆与外接圆的圆心,OC⊥AB于C,
∵正多边形的内切圆与外接圆的半径之比为,
∴=,
在Rt△AOC中,cos∠AOC==,
∴∠AOC=45°,
∴∠AOB=2∠AOC=90°,
则正多边形边数为:=4.
故选:C.
14.解:如图,连接AE,EI,AH,过点J作JM⊥EI于M.
∵ABCDEF是正六边形,
∴∠DEF=∠F=120°,
∵FA=FE,
∴∠FEA=∠FAE=30°,
∴∠AED=90°,
同法可证,∠DEI=∠EIH=90°,
∴∠AED+∠DEI=180°,
∴A,E,I共线,
设IH=IJ=JE=a,
∵JM⊥EI,
∴EM=MI=a,
∴AI=2EI=2a,
∵∠API=∠AHI,
∴tan∠API=tan∠AHI===2,
故选:A.
15.解:如图,连接OM,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,OM=OF,
∴△OFM是等边三角形,
∴OM=OF=FM=2.
则⊙O的半径为2.
故选:C.
16.解:如图,过点H作FA的延长线的垂线HQ,
∵∠BAF=120°,
∴∠HAQ=60°,∠HQA=90°,
∴∠AHQ=30°,
设AH=x,∴AQ=x,QH=x,
∴BH=B′H=AB﹣AH=6﹣x,
∵AB′=AB=3,
∴B′Q=B′A+AQ=3+x,
在Rt△B′HQ中,根据勾股定理,得
B′H2=B′Q2+QH2,
∴(6﹣x)2=(3+x)2+x2,
解得x=,
∴B′H=6﹣x==,
∵∠HAB′=∠F=∠HB′M=120°,
∴∠AHB′+∠AB′H=60°,∠FB′M+∠AB′H=60°,
∴∠AHB′=∠FB′M,
∴△AB′M∽△FMB′,
∴=,
∴=,
解得B′M=7,
∴C′M=B′M﹣B′C′=7﹣6=1.
故选:A.
17.解:∵五边形ABCDE是正五边形,
∴∠AED=∠EAB=∠ABC=108°,
∵BA=BC,
∴∠BAC=∠BCA=36°,
∴∠EAC=72°,
∴∠AED+∠EAC=180°,
∴DE∥AF,
∵AE=AF=DE,
∴四边形AEDF是菱形,
∴∠EDF=∠EAF=72°,
∵∠EDC=108°,
∴∠FDC=36°,
故选:C.
18.解:延长正五边形的相邻两边,交于圆心,
∵正五边形的外角等于360°÷5=72°,
∴延长正五边形的相邻两边围成的角的度数为:180°﹣72°﹣72°=36°,
∴360°÷36°=10,
∴排成圆环需要10个正五边形,
故选:D.
19.解:∵点M、N以相同的速度中⊙O上逆时针运动,
∴=,
∴∠BAM=∠NBC,
∴∠APN=∠ABP+∠NBC,
∵∠APN=∠ABP+∠BAM=∠ABP+∠CBN=∠ABC,
∴∠APN的度数等于多边形的内角的度数,
当正多边形为n边形时,其内角和为(n﹣2)180°,
∵每个内角的度数为,
∴∠APN=,
故选:B.
20.解:如图,连接AC、BD、OF,
设⊙O的半径是r,
则OF=r,
∵AO是∠EAF的平分线,
∴∠OAF=60°÷2=30°,
∵OA=OF,
∴∠OFA=∠OAF=30°,
∴∠COF=30°+30°=60°,
∴FI=r sin60°=r,
∴EF=r×2=r,
∵AO=2OI,
∴OI=r,CI=r﹣r=r,
∴==,
∴GH=BD=r,
∴==.
故选:C.
21.解:设正六边形的边长为a.则S△PCD=2×a2=a2,S四边形BCDE=3×a2=a2,
由题意MN是△PCD的中位线,
∴S△PMN=S△PCD=a2,
∴S四边形MNDC=a2﹣a2=a2,
∴S△BMC=S△DNE=(a2﹣a2)=a2,
∵PM=CM,
∴S△PBM=S△BMC=a2,
∴S△PBM:S四边形MCDN=a2:a2=1:2,
故选:A.
22.解:∵AF是⊙O的直径,五边形ABCDE是⊙O的内接正五边形,
∴,,∠BAE=108°,
∴,
∴∠BAF=∠BAE=54°,
∴∠BDF=∠BAF=54°,
故选:C.
23.解:连接OA、OC.
∵五边形ABCDE是正五边形,
∴∠AOB==72°,
∴∠AOC=72°×2=144°,
∵△AMN是正三角形,
∴∠AOM==120°,
∴∠COM=∠AOC﹣∠AOM=144°﹣120°=24°,
∴∠MBC=∠COM=×24°=12°.
故选:A.
24.解:连接BD,如图所示:
由正六边形和正方形的性质得:B、D、H三点共线,
设正六边形的边长为a,则AB=BC=CD=DE=a,
∵在△BCD中,BC=CD=a,∠BCD=120°,
∴BD=a.
∴BH=DB+DH=(+1)a.
在Rt△ABH中,tan∠HAB==+1.
故选:B.
25.解:设AD与BE交于点R,AC与BD交于点H,AD与CE交于点J,连接RQ,如图所示:
∵由五角星的性质可知:△APR≌△BHP≌△CQH≌△DJQ≌△ERJ,AP=AR,JR=JQ=HQ=HP,AR=CQ,
∴RQ∥AC,
同理:PQ∥AD,
∴四边形APQR为平行四边形,
∵AP=AR,
∴四边形APQR为菱形,
∴△APR与△PQR面积相等,PQ=RQ,
在△HPQ和△JRQ中,,
∴△HPQ≌△JRQ(SSS),
∴△HPQ和△JRQ的面积相等,
设△APR的面积为S1,△HPQ的面积为S2,
则1=6S1+2S2,
∴SAPQD=3S1+S2=,
故选:D.
