2021-2022学年苏科版九年级数学下册5.2 二次函数y=ax2+bx+c图象与性质 同步强化训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册5.2 二次函数y=ax2+bx+c图象与性质 同步强化训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 14:22:20 | ||
图片预览




文档简介
2021-2022学年苏科版九年级数学下
《5.2 二次函数y=ax2+bx+c图象与性质》同步强化训练
(时间:90分钟 满分:120分)
一.选择题(每小题2分 共30分)
1.抛物线y=x2-2x+2的顶点坐标为( )
A.(1,1) B.(-1,1) C.(1,3) D.(-1,3)
2.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线相应的函数表达式是 ( )
A.y=(x+2)2+1 B.y=(x+2)2-1 C.y=(x-2)2+1 D.y=(x-2)2-1
3.在二次函数y=x2-2x-3中,当0≤x≤3时,y的最大值和最小值分别是( )
A.0,-4 B.0,-3 C.-3,-4 D.0,0
4.抛物线y=2x2-5x+6的对称轴是( )
A. 直线x= B. 直线x= C. 直线x=- D. 直线x=-
5.将二次函数y=x2-2x+3化为y=(x-m)2+k的形式,结果为( )
A. y=(x+1)2+4 B. y=(x+1)2+2 C. y=(x-1)2+4 D. y=(x-1)2+2
6.二次函数y=-2x2+4x-9的图象的最高点的纵坐标是( )
A. 7 B. -7 C. 9 D. -9
7﹒已知抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,那么抛物线的对称轴( )
A.只能是x=-1 B.可能是y轴
C.在y轴右侧且在直线x=2的左侧 D.在y轴左侧且在直线x=-2的右侧
8.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1,y2,y3的大小关系为 ( )
A.y1>y2>y3 B.y1y2>y1 D.y2>y1>y3
9.关于二次函数y=2x2+4x-1,下列说法正确的是( )
A.函数图像与y轴的交点坐标为(0,1) B.函数图像的对称轴在y轴的右侧
C.当x<0时,y的值随x值的增大而减小 D.y的最小值为-3
10.如图抛物线y=ax2+bx+c过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
A.-3<P<-1 B.-6<P<0 C.-3<P<0 D.-6<P<-3
第10题图 第12题图 第13题图 第14题图 第15题图
11﹒已知二次函数y=x2+(m-1)x+1,当x>1时,y随x的增大而增大,则m的取值范围是( )
A.m=-1 B.m=3 C.m≤-1 D.m≥-1
12﹒已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是-4
C.抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的横坐标分别是-1,3
D.当x<1时,y随x的增大而增大
13.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:①abc<0;②2a+b=0;③a-b+c>0;④4a-2b+c<0.其中正确的是( )
A.①② B.只有① C.③④ D.①④
14.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A. a>0 B. c<0 C. x=3是方程ax2+bx+c=0的一个根 D. abc>0
15.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1和3,则下列结论正确的是( )
A. 2a-b=0 B. a+b+c>0 C. 3a-c=0 D. 当a=时,△ABD是等腰直角三角形
二.填空题(每小题2分 共20分)
16.已知二次函数y=(x-2)2+3,当x_______时,y随x的增大而减小.
17.抛物线y=x2+2x的顶点坐标为________,对称轴是直线____.
18.已知抛物线y=-x2-2x+3,当-2≤x≤2时,对应的函数值y的取值范围为________.
19.若抛物线y=x2-4x+k的顶点的纵坐标为n,则k-n的值为______.
20.请写出一个以直线x=﹣3为对称轴,且在对称轴右侧部分是下降的抛物线的表达式,这条抛物线的表达式可以是_______________________.
21.已知抛物线y=x2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB∥x轴,其中点A的坐标为(0,3),则点B的坐标为________________.
22.已知点A(-3,7)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴对称的点的坐标为______________.
23.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为____________.
第23题图 第24题图 第25题图
24.如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=﹣2,点C在抛物线上,且位于点A、B之间(C不与A、B重合)若△ABC的周长为a,则四边形AOBC的周长为________.(用含a的式子表示)
25.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是___________.
(写序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
三.解答题(70分)
26.(9分)已知二次函数y=﹣x2﹣x+.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出抛物线的顶点坐标以及抛物线与x轴的两个交点坐标;
(3)若将此图象沿x轴向右平移3个单位,请在坐标系中画出平移后的图象,并写出平移后图象所对应的函数关系式.
27.(9分)设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
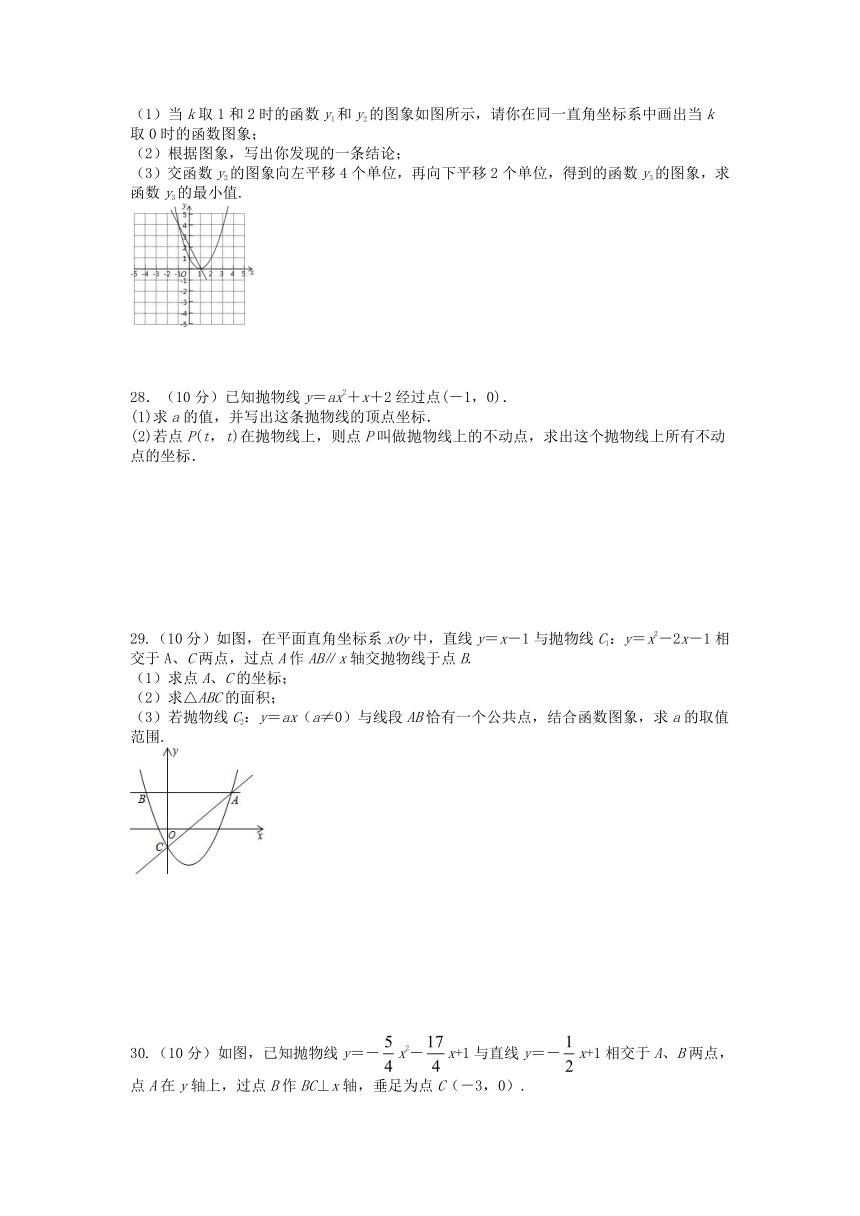
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k
取0时的函数图象;
(2)根据图象,写出你发现的一条结论;
(3)交函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
28.(10分)已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
29.(10分)如图,在平面直角坐标系xOy中,直线y=x-1与抛物线C1:y=x2-2x-1相交于A、C两点,过点A作AB∥x轴交抛物线于点B.
(1)求点A、C的坐标;
(2)求△ABC的面积;
(3)若抛物线C2:y=ax(a≠0)与线段AB恰有一个公共点,结合函数图象,求a的取值范围.
30.(10分)如图,已知抛物线y=-x2-x+1与直线y=-x+1相交于A、B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
(1)若点N是抛物线上一点(点N在AB上方),过点N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(2)在(1)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
31.(10分)如图,二次函数y=ax2+bx的图象经过点A(2,4),B(6,0).
(1)求a,b的值.
(2)若C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),请写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
32.(12分)如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的函数表达式.
(2)在抛物线的对称轴直线x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标.
(3)设P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
教师样卷
一.选择题(每小题2分 共30分)
1.抛物线y=x2-2x+2的顶点坐标为( A )
A.(1,1) B.(-1,1) C.(1,3) D.(-1,3)
[解析] 将所给抛物线的表达式配方成顶点式,得y=(x-1)2+1.由顶点式得抛物线的顶点坐标是(1,1),故选A.
2.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线相应的函数表达式是 ( C )
A.y=(x+2)2+1 B.y=(x+2)2-1 C.y=(x-2)2+1 D.y=(x-2)2-1
3.在二次函数y=x2-2x-3中,当0≤x≤3时,y的最大值和最小值分别是( A )
A.0,-4 B.0,-3 C.-3,-4 D.0,0
[解析] A 抛物线的对称轴是直线x=1,且抛物线开口向上,则在0≤x≤3的范围内,当x=1时,y=1-2-3=-4,是最小值;当x=3时,y=9-6-3=0,是最大值.故选A.
4.抛物线y=2x2-5x+6的对称轴是(A)
A. 直线x= B. 直线x= C. 直线x=- D. 直线x=-
5.将二次函数y=x2-2x+3化为y=(x-m)2+k的形式,结果为(D)
A. y=(x+1)2+4 B. y=(x+1)2+2 C. y=(x-1)2+4 D. y=(x-1)2+2
6.二次函数y=-2x2+4x-9的图象的最高点的纵坐标是(B)
A. 7 B. -7 C. 9 D. -9
7﹒已知抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,那么抛物线的对称轴( D )
A.只能是x=-1 B.可能是y轴
C.在y轴右侧且在直线x=2的左侧 D.在y轴左侧且在直线x=-2的右侧
8.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1,y2,y3的大小关系为 ( A )
A.y1>y2>y3 B.y1y2>y1 D.y2>y1>y3
[解析] 方法一:把A,B,C三点的坐标分别代入y=-(x+1)2+m,得y1=-1+m,y2=-4+m,y3=-9+m,所以y1>y2>y3.方法二:抛物线y=-(x+1)2+m的开口向下,对称轴为直线x=-1,点B,C都在对称轴的右边,由点A(-2,y1)可知点(0,y1)也在抛物线上.根据二次函数图像的性质,可知当x>-1时,y随x的增大而减小,而0<1<2,所以y1>y2>y3.
9.关于二次函数y=2x2+4x-1,下列说法正确的是( D )
A.函数图像与y轴的交点坐标为(0,1) B.函数图像的对称轴在y轴的右侧
C.当x<0时,y的值随x值的增大而减小 D.y的最小值为-3
[解析] y=2x2+4x-1=2(x+1)2-3.当x=0时,y=-1,所以图像与y轴的交点坐标为(0,-1),故选项A错误;图像的对称轴是直线x=-1,在y轴的左侧,故选项B错误;因为抛物线的对称轴是直线x=-1,开口向上,所以当x<-1时,y的值随x的增大而减小,故选项C错误;二次函数y=2x2+4x-1的顶点坐标是(-1,-3),所以当x=-1时,y的最小值为-3,故选项D正确.
10.如图抛物线y=ax2+bx+c过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( B )
A.-3<P<-1 B.-6<P<0 C.-3<P<0 D.-6<P<-3
[解析] ∵抛物线y=ax2+bx+c过点(-1,0)和点(0,-3),∴0=a-b+c,-3=c,∴b=a-3,∴P=a+b+c=a+a-3-3=2a-6.∵抛物线的顶点在第四象限,a>0,∴b=a-3<0,∴a<3,∴0<a<3,∴-6<2a-6<0,即-6<P<0.故选B.
第10题图 第12题图 第13题图 第14题图 第15题图
11﹒已知二次函数y=x2+(m-1)x+1,当x>1时,y随x的增大而增大,则m的取值范围是( D )
A.m=-1 B.m=3 C.m≤-1 D.m≥-1
12﹒已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( D )
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是-4
C.抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的横坐标分别是-1,3
D.当x<1时,y随x的增大而增大
13.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:①abc<0;②2a+b=0;③a-b+c>0;④4a-2b+c<0.其中正确的是( D )
A.①② B.只有① C.③④ D.①④
14.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是(C)
A. a>0 B. c<0 C. x=3是方程ax2+bx+c=0的一个根 D. abc>0
第4题图 第6题图
15.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1和3,则下列结论正确的是(D)
A. 2a-b=0 B. a+b+c>0 C. 3a-c=0 D. 当a=时,△ABD是等腰直角三角形
【解】 ∵抛物线与x轴的交点A,B的横坐标分别为-1,3,∴抛物线的对称轴为直线x=1,即-=1,∴2a+b=0,故A错误.当x=1时,y<0,即a+b+c<0,故B错误.
∵点A的坐标为(-1,0),∴a-b+c=0.又∵b=-2a,∴a+2a+c=0,即3a+c=0,故C错误.∵当a=时,b=-1,c=-,∴抛物线的函数表达式为y=x2-x-.把x=1代入,得y=-1-=-2,∴点D的坐标为(1,-2).设对称轴x=1与x轴的为E,
如解图,则AE=2,BE=2,DE=2,∴△ADE和△BDE都是等腰直角三角形,∴∠DAE=∠DBE=45°,∴△ABD是等腰直角三角形,故D正确.
二.填空题(每小题2分 共20分)
16.已知二次函数y=(x-2)2+3,当x___<2_____时,y随x的增大而减小.
[解析] 在y=(x-2)2+3中,a=1.∵a>0,∴函数的图像开口向上.∵函数图像的对称轴为直线x=2,∴当x<2时,y的值随x的增大而减小;当x>2时,y的值随x的增大而增大.
17.抛物线y=x2+2x的顶点坐标为_(-1,-1)_______,对称轴是直线__x=-1__.
[解析] ∵y=x2+2x=(x+1)2-1,∴抛物线y=x2+2x的顶点坐标是(-1,-1),对称轴是直线x=-1.
18.已知抛物线y=-x2-2x+3,当-2≤x≤2时,对应的函数值y的取值范围为___-5≤y≤4_____.
[解析] ∵y=-x2-2x+3=-(x+1)2+4,∴抛物线y=-x2-2x+3的顶点坐标为(-1,4).∵抛物线开口向下,∴当x=-1时,y取得最大值为4.又∵2与抛物线对称轴直线x=-1的距离远,且当x=2时,y=-4-4+3=-5,∴当-2≤x≤2时,-5≤y≤4.故答案为-5≤y≤4.
19.若抛物线y=x2-4x+k的顶点的纵坐标为n,则k-n的值为___4___.
解答:∵抛物线y=x2-4x+k的顶点的纵坐标为n,∴=n,∴k-n=4,
故答案为:4.
20.请写出一个以直线x=﹣3为对称轴,且在对称轴右侧部分是下降的抛物线的表达式,这条抛物线的表达式可以是___不唯一,如y=-(x+3)2+2____________________.
解答:本题答案不唯一,如y=-(x+3)2+2,故答案为:y=-(x+3)2+2,不唯一.
21.已知抛物线y=x2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB∥x轴,其中点A的坐标为(0,3),则点B的坐标为___(4,3)_____________.
解答:由题意知:A、B两点的纵坐标相等,且到对称轴的距离相等,∴点B的坐标为(4,3),故答案为:(4,3).
22.已知点A(-3,7)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴对称的点的坐标为___(-1,7)___________.
解答:抛物线的对称轴为直线x=-2,设点A关于对称轴对称的点的坐标为(x,7),
则=-2,解得:x=-1,所以对称点的坐标为(-1,7),故答案为:(-1,7).
23.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为_____1_______.
解答:∵y=x2-2x+2=(x-1)2+1,∴抛物线的顶点坐标为(1,1),∵四边形ABCD为矩形,∴BD=AC,∵AC⊥x轴,∴AC的长等于点A的纵坐标,当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为1,∴对角线BD的最小值为1,故答案为:1.
第23题图 第24题图 第25题图
24.如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=﹣2,点C在抛物线上,且位于点A、B之间(C不与A、B重合)若△ABC的周长为a,则四边形AOBC的周长为__a+4_______.(用含a的式子表示)
解答:如图,∵对称轴为直线x=﹣2,抛物线经过原点、x轴负半轴交于点B,∴OB=4,
∵由抛物线的对称性知AB=AO,∴四边形AOBC的周长为AO+AC+BC+OB=△ABC的周长+OB=a+4,故答案为:a+4.
25.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是___③④________.
(写序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
解答:∵抛物线开口向上,∴a>0,又∵对称轴为x=->0,∴b<0,故①不正确;
∵x=-1时,y>0,∴a-b+c>0,故②不正确;∵抛物线向右平移了2个单位,∴平行四边形的底为2,∵函数y=ax2+bx+c的最小值是y=-2,∴平行四边形的高是2,∴阴影部分的面积是:2×2=4,故③正确;由=-2,得c=-1,∴b2=4a,故④正确,综合上述,结论正确的有:③④,故答案为:③④.
三.解答题(70分)
26.(9分)已知二次函数y=﹣x2﹣x+.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出抛物线的顶点坐标以及抛物线与x轴的两个交点坐标;
(3)若将此图象沿x轴向右平移3个单位,请在坐标系中画出平移后的图象,并写出平移后图象所对应的函数关系式.
解答:(1)画函数图象如图所示:
(2)抛物线的顶点坐标为(-1,2);抛物线与x轴的两个交点坐标(-3,0),(1,0);(3)∵y=﹣x2﹣x+=﹣(x+1)2+2,∴平移后的函数关系式为y=﹣(x+1-3)2+2=﹣(x-2)2+2,即y=﹣x2+2x.
27.(9分)设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k
取0时的函数图象;
(2)根据图象,写出你发现的一条结论;
(3)交函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
解答:(1)当k=0时,y=-(x-1)(x+3),所画函数图象如图所示:
(2)①根据图象可知,图象都经过点(1,0)和(-1,4);
②图象与x轴的交点是(1,0);③k取0和2时的函数图象关于点(0,2)中心对称;和(-1,4)等.(3)平移后的函数y3的表达式为y3=(x+3)2-2,所以当x=-3时,函数y3的最小值是-2.
28.(10分)已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
【解】 (1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-+,其顶点坐标是.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=,t2=-.
∴此抛物线上的不动点有两个,即点P1(,),P2(-,-).
29.(10分)如图,在平面直角坐标系xOy中,直线y=x-1与抛物线C1:y=x2-2x-1相交于A、C两点,过点A作AB∥x轴交抛物线于点B.
(1)求点A、C的坐标(2)求△ABC的面积;(3)若抛物线C2:y=ax(a≠0)与线段AB恰有一个公共点,结合函数图象,求a的取值范围.
解答:(1)由,得:,,∴点A、C的坐标分别为(3,2),(0,-1);(2)由题意知:点A与B关于抛物线C1的对称轴对称,∵抛物线C1的对称轴为x=1,且A(3,2),∴B(-1,2),∴AB=4,设直线AB与y轴交于点D,则CD=1+2=3,∴S△ABC=ABCD=×4×3=6;(3)如图,当C2过点A点,B点临界点时,把A(3,2)代入y=ax2得:a=,把B(-1,2)代入y=ax2得:a=2,∴a的取值范围为≤a<2.
30.(10分)如图,已知抛物线y=-x2-x+1与直线y=-x+1相交于A、B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
(1)若点N是抛物线上一点(点N在AB上方),过点N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(2)在(1)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
解答:(1)∵点A在y轴上,且直线y=-x+1经过点A,∴当x=0时,y=1,∴A(0,1),∵BC⊥x轴,且C(-3,0),∴当x=-3时,y=-×(-3)+1=,
∴B(-3,),∵点N是抛物线y=-x2-x+1上,∴可设N(x,-x2-x+1),则M,P点的坐标分别为(x,-x+1),(x,0),∴MN=PN-PM=-x2-x+1-(-x+1)=-x2-x=-(x+)2+,∴当x=-时,MN的最大值为;
(2)如图,连接BN,BM,BM与NC互相垂直平分,则四边形BCMN是菱形,
∴BC∥MN,MN=BC,且BC=MC,∴-x2-x=,且(-x+1)2+(x+3)2=,
解得:x=-1,则y=4,故当N的坐标为(-1,4)时,BM和NC互相垂直平分.
31.(10分)如图,二次函数y=ax2+bx的图象经过点A(2,4),B(6,0).
(1)求a,b的值.
(2)若C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),请写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
【解】 (1)将点A(2,4),B(6,0)的坐标分别代入y=ax2+bx,
得解得
(2)如解图,过点A作x轴的垂线,垂足为D(2,0),过点C作CE⊥AD,CF⊥x轴,垂足分别为E,F,连结AC,BC,CD.则S△OAD=OD·AD=×2×4=4,S△ACD=AD·CE=×4×(x-2)=2x-4,S△BCD=BD·CF=×(6-2)×=-x2+6x,∴S=S△OAD+S△ACD+S△BCD=4+2x-4-x2+6x=-x2+8x,∴S关于x的函数表达式为S=-x2+8x(2<x<6).∵S=-x2+8x=-(x-4)2+16,∴当x=4时,四边形OACB的面积S有最大值,最大值为16.
32.(12分)如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的函数表达式.
(2)在抛物线的对称轴直线x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标.
(3)设P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
【解】 (1)由题意,得解得∴抛物线的函数表达式为y=-x2-2x+3.∵抛物线的对称轴为直线x=-1,且抛物线经过点A(1,0),∴点B(-3,0).
把点B(-3,0),C(0,3)的坐标分别代入y=mx+n,得解得
∴直线BC的函数表达式为y=x+3.
(2)∵点A与点B关于直线x=-1对称,∴直线BC与对称轴x=-1的交点就是使MA+MC的值最小的点M.把x=-1代入y=x+3,得y=2,∴点M(-1,2).
(3)如解图,设点P(-1,t).∵点B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10.①若点B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10,解得t=-2.②若点C为直角顶点,则BC2+PC2=PB2,即18+t2-6t+10=4+t2,解得t=4.③若点P为直角顶点,则PB2+PC2=BC2,即4+t2+t2-6t+10=18,解得t1=,t2=.综上所述,点P的坐标为(-1,-2)或(-1,4)或 或.
《5.2 二次函数y=ax2+bx+c图象与性质》同步强化训练
(时间:90分钟 满分:120分)
一.选择题(每小题2分 共30分)
1.抛物线y=x2-2x+2的顶点坐标为( )
A.(1,1) B.(-1,1) C.(1,3) D.(-1,3)
2.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线相应的函数表达式是 ( )
A.y=(x+2)2+1 B.y=(x+2)2-1 C.y=(x-2)2+1 D.y=(x-2)2-1
3.在二次函数y=x2-2x-3中,当0≤x≤3时,y的最大值和最小值分别是( )
A.0,-4 B.0,-3 C.-3,-4 D.0,0
4.抛物线y=2x2-5x+6的对称轴是( )
A. 直线x= B. 直线x= C. 直线x=- D. 直线x=-
5.将二次函数y=x2-2x+3化为y=(x-m)2+k的形式,结果为( )
A. y=(x+1)2+4 B. y=(x+1)2+2 C. y=(x-1)2+4 D. y=(x-1)2+2
6.二次函数y=-2x2+4x-9的图象的最高点的纵坐标是( )
A. 7 B. -7 C. 9 D. -9
7﹒已知抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,那么抛物线的对称轴( )
A.只能是x=-1 B.可能是y轴
C.在y轴右侧且在直线x=2的左侧 D.在y轴左侧且在直线x=-2的右侧
8.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1,y2,y3的大小关系为 ( )
A.y1>y2>y3 B.y1
9.关于二次函数y=2x2+4x-1,下列说法正确的是( )
A.函数图像与y轴的交点坐标为(0,1) B.函数图像的对称轴在y轴的右侧
C.当x<0时,y的值随x值的增大而减小 D.y的最小值为-3
10.如图抛物线y=ax2+bx+c过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
A.-3<P<-1 B.-6<P<0 C.-3<P<0 D.-6<P<-3
第10题图 第12题图 第13题图 第14题图 第15题图
11﹒已知二次函数y=x2+(m-1)x+1,当x>1时,y随x的增大而增大,则m的取值范围是( )
A.m=-1 B.m=3 C.m≤-1 D.m≥-1
12﹒已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( )
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是-4
C.抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的横坐标分别是-1,3
D.当x<1时,y随x的增大而增大
13.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:①abc<0;②2a+b=0;③a-b+c>0;④4a-2b+c<0.其中正确的是( )
A.①② B.只有① C.③④ D.①④
14.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( )
A. a>0 B. c<0 C. x=3是方程ax2+bx+c=0的一个根 D. abc>0
15.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1和3,则下列结论正确的是( )
A. 2a-b=0 B. a+b+c>0 C. 3a-c=0 D. 当a=时,△ABD是等腰直角三角形
二.填空题(每小题2分 共20分)
16.已知二次函数y=(x-2)2+3,当x_______时,y随x的增大而减小.
17.抛物线y=x2+2x的顶点坐标为________,对称轴是直线____.
18.已知抛物线y=-x2-2x+3,当-2≤x≤2时,对应的函数值y的取值范围为________.
19.若抛物线y=x2-4x+k的顶点的纵坐标为n,则k-n的值为______.
20.请写出一个以直线x=﹣3为对称轴,且在对称轴右侧部分是下降的抛物线的表达式,这条抛物线的表达式可以是_______________________.
21.已知抛物线y=x2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB∥x轴,其中点A的坐标为(0,3),则点B的坐标为________________.
22.已知点A(-3,7)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴对称的点的坐标为______________.
23.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为____________.
第23题图 第24题图 第25题图
24.如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=﹣2,点C在抛物线上,且位于点A、B之间(C不与A、B重合)若△ABC的周长为a,则四边形AOBC的周长为________.(用含a的式子表示)
25.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是___________.
(写序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
三.解答题(70分)
26.(9分)已知二次函数y=﹣x2﹣x+.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出抛物线的顶点坐标以及抛物线与x轴的两个交点坐标;
(3)若将此图象沿x轴向右平移3个单位,请在坐标系中画出平移后的图象,并写出平移后图象所对应的函数关系式.
27.(9分)设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k
取0时的函数图象;
(2)根据图象,写出你发现的一条结论;
(3)交函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
28.(10分)已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
29.(10分)如图,在平面直角坐标系xOy中,直线y=x-1与抛物线C1:y=x2-2x-1相交于A、C两点,过点A作AB∥x轴交抛物线于点B.
(1)求点A、C的坐标;
(2)求△ABC的面积;
(3)若抛物线C2:y=ax(a≠0)与线段AB恰有一个公共点,结合函数图象,求a的取值范围.
30.(10分)如图,已知抛物线y=-x2-x+1与直线y=-x+1相交于A、B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
(1)若点N是抛物线上一点(点N在AB上方),过点N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(2)在(1)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
31.(10分)如图,二次函数y=ax2+bx的图象经过点A(2,4),B(6,0).
(1)求a,b的值.
(2)若C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),请写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
32.(12分)如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的函数表达式.
(2)在抛物线的对称轴直线x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标.
(3)设P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
教师样卷
一.选择题(每小题2分 共30分)
1.抛物线y=x2-2x+2的顶点坐标为( A )
A.(1,1) B.(-1,1) C.(1,3) D.(-1,3)
[解析] 将所给抛物线的表达式配方成顶点式,得y=(x-1)2+1.由顶点式得抛物线的顶点坐标是(1,1),故选A.
2.将抛物线y=x2向右平移2个单位长度,再向上平移1个单位长度,所得抛物线相应的函数表达式是 ( C )
A.y=(x+2)2+1 B.y=(x+2)2-1 C.y=(x-2)2+1 D.y=(x-2)2-1
3.在二次函数y=x2-2x-3中,当0≤x≤3时,y的最大值和最小值分别是( A )
A.0,-4 B.0,-3 C.-3,-4 D.0,0
[解析] A 抛物线的对称轴是直线x=1,且抛物线开口向上,则在0≤x≤3的范围内,当x=1时,y=1-2-3=-4,是最小值;当x=3时,y=9-6-3=0,是最大值.故选A.
4.抛物线y=2x2-5x+6的对称轴是(A)
A. 直线x= B. 直线x= C. 直线x=- D. 直线x=-
5.将二次函数y=x2-2x+3化为y=(x-m)2+k的形式,结果为(D)
A. y=(x+1)2+4 B. y=(x+1)2+2 C. y=(x-1)2+4 D. y=(x-1)2+2
6.二次函数y=-2x2+4x-9的图象的最高点的纵坐标是(B)
A. 7 B. -7 C. 9 D. -9
7﹒已知抛物线y=ax2+bx+c(a>0)过(-2,0),(2,3)两点,那么抛物线的对称轴( D )
A.只能是x=-1 B.可能是y轴
C.在y轴右侧且在直线x=2的左侧 D.在y轴左侧且在直线x=-2的右侧
8.设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=-(x+1)2+m上的三点,则y1,y2,y3的大小关系为 ( A )
A.y1>y2>y3 B.y1
[解析] 方法一:把A,B,C三点的坐标分别代入y=-(x+1)2+m,得y1=-1+m,y2=-4+m,y3=-9+m,所以y1>y2>y3.方法二:抛物线y=-(x+1)2+m的开口向下,对称轴为直线x=-1,点B,C都在对称轴的右边,由点A(-2,y1)可知点(0,y1)也在抛物线上.根据二次函数图像的性质,可知当x>-1时,y随x的增大而减小,而0<1<2,所以y1>y2>y3.
9.关于二次函数y=2x2+4x-1,下列说法正确的是( D )
A.函数图像与y轴的交点坐标为(0,1) B.函数图像的对称轴在y轴的右侧
C.当x<0时,y的值随x值的增大而减小 D.y的最小值为-3
[解析] y=2x2+4x-1=2(x+1)2-3.当x=0时,y=-1,所以图像与y轴的交点坐标为(0,-1),故选项A错误;图像的对称轴是直线x=-1,在y轴的左侧,故选项B错误;因为抛物线的对称轴是直线x=-1,开口向上,所以当x<-1时,y的值随x的增大而减小,故选项C错误;二次函数y=2x2+4x-1的顶点坐标是(-1,-3),所以当x=-1时,y的最小值为-3,故选项D正确.
10.如图抛物线y=ax2+bx+c过点(-1,0)和点(0,-3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( B )
A.-3<P<-1 B.-6<P<0 C.-3<P<0 D.-6<P<-3
[解析] ∵抛物线y=ax2+bx+c过点(-1,0)和点(0,-3),∴0=a-b+c,-3=c,∴b=a-3,∴P=a+b+c=a+a-3-3=2a-6.∵抛物线的顶点在第四象限,a>0,∴b=a-3<0,∴a<3,∴0<a<3,∴-6<2a-6<0,即-6<P<0.故选B.
第10题图 第12题图 第13题图 第14题图 第15题图
11﹒已知二次函数y=x2+(m-1)x+1,当x>1时,y随x的增大而增大,则m的取值范围是( D )
A.m=-1 B.m=3 C.m≤-1 D.m≥-1
12﹒已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法错误的是( D )
A.图象关于直线x=1对称
B.函数y=ax2+bx+c(a≠0)的最小值是-4
C.抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的横坐标分别是-1,3
D.当x<1时,y随x的增大而增大
13.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-1,下列结论:①abc<0;②2a+b=0;③a-b+c>0;④4a-2b+c<0.其中正确的是( D )
A.①② B.只有① C.③④ D.①④
14.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是(C)
A. a>0 B. c<0 C. x=3是方程ax2+bx+c=0的一个根 D. abc>0
第4题图 第6题图
15.如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为D,其图象与x轴的交点A,B的横坐标分别为-1和3,则下列结论正确的是(D)
A. 2a-b=0 B. a+b+c>0 C. 3a-c=0 D. 当a=时,△ABD是等腰直角三角形
【解】 ∵抛物线与x轴的交点A,B的横坐标分别为-1,3,∴抛物线的对称轴为直线x=1,即-=1,∴2a+b=0,故A错误.当x=1时,y<0,即a+b+c<0,故B错误.
∵点A的坐标为(-1,0),∴a-b+c=0.又∵b=-2a,∴a+2a+c=0,即3a+c=0,故C错误.∵当a=时,b=-1,c=-,∴抛物线的函数表达式为y=x2-x-.把x=1代入,得y=-1-=-2,∴点D的坐标为(1,-2).设对称轴x=1与x轴的为E,
如解图,则AE=2,BE=2,DE=2,∴△ADE和△BDE都是等腰直角三角形,∴∠DAE=∠DBE=45°,∴△ABD是等腰直角三角形,故D正确.
二.填空题(每小题2分 共20分)
16.已知二次函数y=(x-2)2+3,当x___<2_____时,y随x的增大而减小.
[解析] 在y=(x-2)2+3中,a=1.∵a>0,∴函数的图像开口向上.∵函数图像的对称轴为直线x=2,∴当x<2时,y的值随x的增大而减小;当x>2时,y的值随x的增大而增大.
17.抛物线y=x2+2x的顶点坐标为_(-1,-1)_______,对称轴是直线__x=-1__.
[解析] ∵y=x2+2x=(x+1)2-1,∴抛物线y=x2+2x的顶点坐标是(-1,-1),对称轴是直线x=-1.
18.已知抛物线y=-x2-2x+3,当-2≤x≤2时,对应的函数值y的取值范围为___-5≤y≤4_____.
[解析] ∵y=-x2-2x+3=-(x+1)2+4,∴抛物线y=-x2-2x+3的顶点坐标为(-1,4).∵抛物线开口向下,∴当x=-1时,y取得最大值为4.又∵2与抛物线对称轴直线x=-1的距离远,且当x=2时,y=-4-4+3=-5,∴当-2≤x≤2时,-5≤y≤4.故答案为-5≤y≤4.
19.若抛物线y=x2-4x+k的顶点的纵坐标为n,则k-n的值为___4___.
解答:∵抛物线y=x2-4x+k的顶点的纵坐标为n,∴=n,∴k-n=4,
故答案为:4.
20.请写出一个以直线x=﹣3为对称轴,且在对称轴右侧部分是下降的抛物线的表达式,这条抛物线的表达式可以是___不唯一,如y=-(x+3)2+2____________________.
解答:本题答案不唯一,如y=-(x+3)2+2,故答案为:y=-(x+3)2+2,不唯一.
21.已知抛物线y=x2+bx+c的对称轴为x=2,点A、B均在抛物线上,且AB∥x轴,其中点A的坐标为(0,3),则点B的坐标为___(4,3)_____________.
解答:由题意知:A、B两点的纵坐标相等,且到对称轴的距离相等,∴点B的坐标为(4,3),故答案为:(4,3).
22.已知点A(-3,7)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴对称的点的坐标为___(-1,7)___________.
解答:抛物线的对称轴为直线x=-2,设点A关于对称轴对称的点的坐标为(x,7),
则=-2,解得:x=-1,所以对称点的坐标为(-1,7),故答案为:(-1,7).
23.如图,在平面直角坐标系中,点A在抛物线y=x2-2x+2上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连接BD,则对角线BD的最小值为_____1_______.
解答:∵y=x2-2x+2=(x-1)2+1,∴抛物线的顶点坐标为(1,1),∵四边形ABCD为矩形,∴BD=AC,∵AC⊥x轴,∴AC的长等于点A的纵坐标,当点A在抛物线的顶点时,点A到x轴的距离最小,最小值为1,∴对角线BD的最小值为1,故答案为:1.
第23题图 第24题图 第25题图
24.如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=﹣2,点C在抛物线上,且位于点A、B之间(C不与A、B重合)若△ABC的周长为a,则四边形AOBC的周长为__a+4_______.(用含a的式子表示)
解答:如图,∵对称轴为直线x=﹣2,抛物线经过原点、x轴负半轴交于点B,∴OB=4,
∵由抛物线的对称性知AB=AO,∴四边形AOBC的周长为AO+AC+BC+OB=△ABC的周长+OB=a+4,故答案为:a+4.
25.如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是___③④________.
(写序号)①b>0;②a-b+c<0;③阴影部分的面积为4;④若c=-1,则b2=4a.
解答:∵抛物线开口向上,∴a>0,又∵对称轴为x=->0,∴b<0,故①不正确;
∵x=-1时,y>0,∴a-b+c>0,故②不正确;∵抛物线向右平移了2个单位,∴平行四边形的底为2,∵函数y=ax2+bx+c的最小值是y=-2,∴平行四边形的高是2,∴阴影部分的面积是:2×2=4,故③正确;由=-2,得c=-1,∴b2=4a,故④正确,综合上述,结论正确的有:③④,故答案为:③④.
三.解答题(70分)
26.(9分)已知二次函数y=﹣x2﹣x+.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出抛物线的顶点坐标以及抛物线与x轴的两个交点坐标;
(3)若将此图象沿x轴向右平移3个单位,请在坐标系中画出平移后的图象,并写出平移后图象所对应的函数关系式.
解答:(1)画函数图象如图所示:
(2)抛物线的顶点坐标为(-1,2);抛物线与x轴的两个交点坐标(-3,0),(1,0);(3)∵y=﹣x2﹣x+=﹣(x+1)2+2,∴平移后的函数关系式为y=﹣(x+1-3)2+2=﹣(x-2)2+2,即y=﹣x2+2x.
27.(9分)设函数y=(x-1)[(k-1)x+(k-3)](k是常数).
(1)当k取1和2时的函数y1和y2的图象如图所示,请你在同一直角坐标系中画出当k
取0时的函数图象;
(2)根据图象,写出你发现的一条结论;
(3)交函数y2的图象向左平移4个单位,再向下平移2个单位,得到的函数y3的图象,求函数y3的最小值.
解答:(1)当k=0时,y=-(x-1)(x+3),所画函数图象如图所示:
(2)①根据图象可知,图象都经过点(1,0)和(-1,4);
②图象与x轴的交点是(1,0);③k取0和2时的函数图象关于点(0,2)中心对称;和(-1,4)等.(3)平移后的函数y3的表达式为y3=(x+3)2-2,所以当x=-3时,函数y3的最小值是-2.
28.(10分)已知抛物线y=ax2+x+2经过点(-1,0).
(1)求a的值,并写出这条抛物线的顶点坐标.
(2)若点P(t,t)在抛物线上,则点P叫做抛物线上的不动点,求出这个抛物线上所有不动点的坐标.
【解】 (1)把点(-1,0)的坐标代入y=ax2+x+2中,得a=-1.
∴此抛物线的函数表达式为y=-x2+x+2=-+,其顶点坐标是.
(2)把点P(t,t)的坐标代入y=-x2+x+2中,
得t=-t2+t+2,解得t1=,t2=-.
∴此抛物线上的不动点有两个,即点P1(,),P2(-,-).
29.(10分)如图,在平面直角坐标系xOy中,直线y=x-1与抛物线C1:y=x2-2x-1相交于A、C两点,过点A作AB∥x轴交抛物线于点B.
(1)求点A、C的坐标(2)求△ABC的面积;(3)若抛物线C2:y=ax(a≠0)与线段AB恰有一个公共点,结合函数图象,求a的取值范围.
解答:(1)由,得:,,∴点A、C的坐标分别为(3,2),(0,-1);(2)由题意知:点A与B关于抛物线C1的对称轴对称,∵抛物线C1的对称轴为x=1,且A(3,2),∴B(-1,2),∴AB=4,设直线AB与y轴交于点D,则CD=1+2=3,∴S△ABC=ABCD=×4×3=6;(3)如图,当C2过点A点,B点临界点时,把A(3,2)代入y=ax2得:a=,把B(-1,2)代入y=ax2得:a=2,∴a的取值范围为≤a<2.
30.(10分)如图,已知抛物线y=-x2-x+1与直线y=-x+1相交于A、B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(-3,0).
(1)若点N是抛物线上一点(点N在AB上方),过点N作NP⊥x轴,垂足为点P,交AB于点M,求MN的最大值;
(2)在(1)的条件下,点N在何位置时,BM与NC相互垂直平分?并求出所有满足条件的N点的坐标.
解答:(1)∵点A在y轴上,且直线y=-x+1经过点A,∴当x=0时,y=1,∴A(0,1),∵BC⊥x轴,且C(-3,0),∴当x=-3时,y=-×(-3)+1=,
∴B(-3,),∵点N是抛物线y=-x2-x+1上,∴可设N(x,-x2-x+1),则M,P点的坐标分别为(x,-x+1),(x,0),∴MN=PN-PM=-x2-x+1-(-x+1)=-x2-x=-(x+)2+,∴当x=-时,MN的最大值为;
(2)如图,连接BN,BM,BM与NC互相垂直平分,则四边形BCMN是菱形,
∴BC∥MN,MN=BC,且BC=MC,∴-x2-x=,且(-x+1)2+(x+3)2=,
解得:x=-1,则y=4,故当N的坐标为(-1,4)时,BM和NC互相垂直平分.
31.(10分)如图,二次函数y=ax2+bx的图象经过点A(2,4),B(6,0).
(1)求a,b的值.
(2)若C是该二次函数图象上A,B两点之间的一动点,横坐标为x(2<x<6),请写出四边形OACB的面积S关于点C的横坐标x的函数表达式,并求S的最大值.
【解】 (1)将点A(2,4),B(6,0)的坐标分别代入y=ax2+bx,
得解得
(2)如解图,过点A作x轴的垂线,垂足为D(2,0),过点C作CE⊥AD,CF⊥x轴,垂足分别为E,F,连结AC,BC,CD.则S△OAD=OD·AD=×2×4=4,S△ACD=AD·CE=×4×(x-2)=2x-4,S△BCD=BD·CF=×(6-2)×=-x2+6x,∴S=S△OAD+S△ACD+S△BCD=4+2x-4-x2+6x=-x2+8x,∴S关于x的函数表达式为S=-x2+8x(2<x<6).∵S=-x2+8x=-(x-4)2+16,∴当x=4时,四边形OACB的面积S有最大值,最大值为16.
32.(12分)如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
(1)若直线y=mx+n经过B,C两点,求直线BC和抛物线的函数表达式.
(2)在抛物线的对称轴直线x=-1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标.
(3)设P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
【解】 (1)由题意,得解得∴抛物线的函数表达式为y=-x2-2x+3.∵抛物线的对称轴为直线x=-1,且抛物线经过点A(1,0),∴点B(-3,0).
把点B(-3,0),C(0,3)的坐标分别代入y=mx+n,得解得
∴直线BC的函数表达式为y=x+3.
(2)∵点A与点B关于直线x=-1对称,∴直线BC与对称轴x=-1的交点就是使MA+MC的值最小的点M.把x=-1代入y=x+3,得y=2,∴点M(-1,2).
(3)如解图,设点P(-1,t).∵点B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10.①若点B为直角顶点,则BC2+PB2=PC2,即18+4+t2=t2-6t+10,解得t=-2.②若点C为直角顶点,则BC2+PC2=PB2,即18+t2-6t+10=4+t2,解得t=4.③若点P为直角顶点,则PB2+PC2=BC2,即4+t2+t2-6t+10=18,解得t1=,t2=.综上所述,点P的坐标为(-1,-2)或(-1,4)或 或.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
