24.1.1 圆 同步练习 2021-2022学年人教版九年级数学上册(word版 含答案)
文档属性
| 名称 | 24.1.1 圆 同步练习 2021-2022学年人教版九年级数学上册(word版 含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 375.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十四章 圆 24.1.1 圆 同步练习
一、选择题
1.已知是直径为10的圆的一条弦,则的长度不可能是( )
A.2 B.5 C.9 D.11
2.若一个圆的半径为,那么该圆的面积等于( )
A. B. C. D.
3.如图,以O为圆心的两个圆中,大圆的半径分别交小圆于点C,D,连结,下列选项中不一定正确的是( )
A. B. C. D.
4.如图,正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点B顺时针旋转α度,使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等,则旋转角度α等于( )
A.36° B.30° C.25° D.22.5°
5.如图,在中,,则的角度是( )
A. B. C. D.
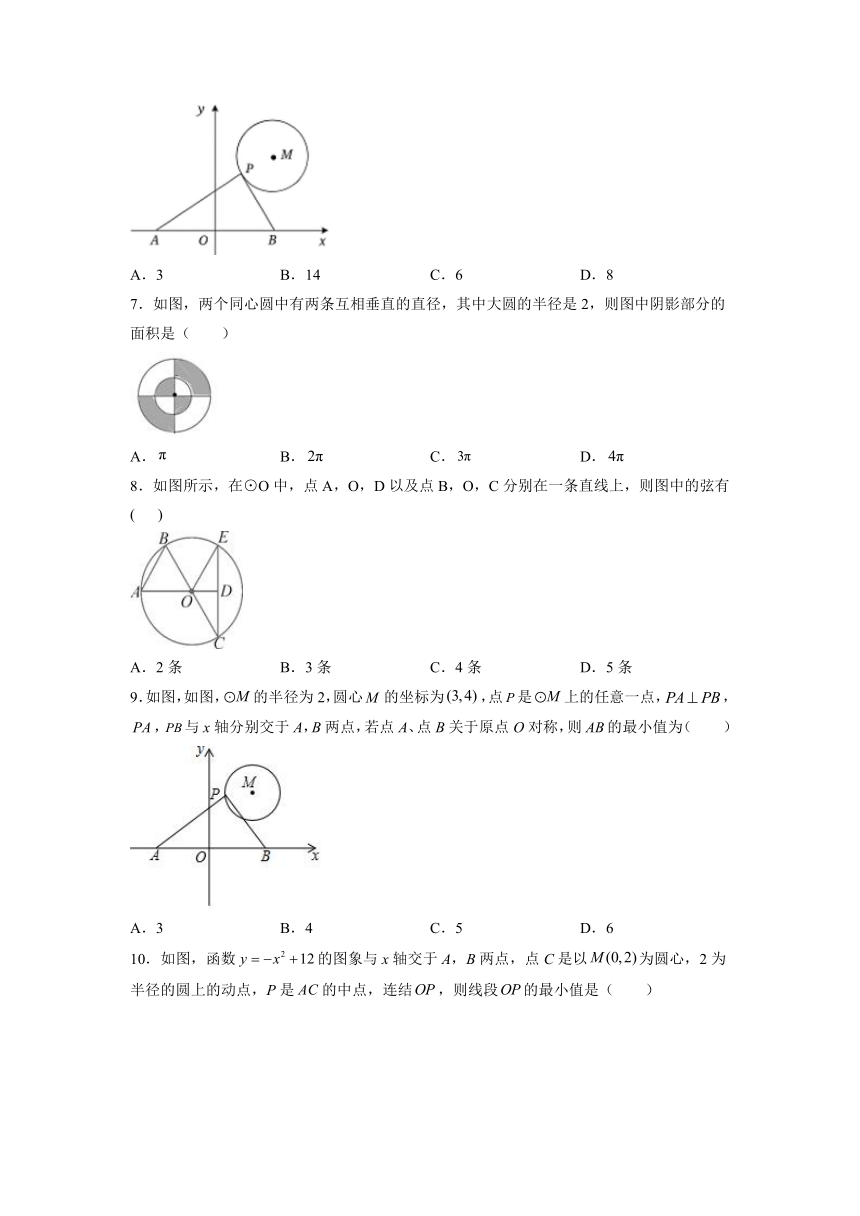
6.如图,⊙M的半径为2,圆心M的坐标为,点P是⊙M上的任意一点,PA⊥PB,且PA、PB与轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最大值为( )
A.3 B.14 C.6 D.8
7.如图,两个同心圆中有两条互相垂直的直径,其中大圆的半径是2,则图中阴影部分的面积是( )
A. B. C. D.
8.如图所示,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条 B.3条 C.4条 D.5条
9.如图,如图,的半径为2,圆心的坐标为,点是上的任意一点,,,与x轴分别交于A,B两点,若点A、点B关于原点O对称,则的最小值为( )
A.3 B.4 C.5 D.6
10.如图,函数的图象与x轴交于A,B两点,点C是以为圆心,2为半径的圆上的动点,P是的中点,连结,则线段的最小值是( )
A.1 B. C.2 D.
二、填空题
11.圆外一点到圆的最大距离为9cm,最小距离为4cm,则圆的半径是_____cm.
12.已知P为⊙O外的一点,P到⊙O上的点的最大距离为6,最小距离为2.若AB为⊙O内一条长为1的弦,则点P到AB的距离的最大值为_____,最小值为_____.
13.如图,平面直角坐标系中,点的坐标是,点是上一点,的半径为2,连接,则线段OB的最小值为__________.
14.图1是传统的手工磨豆腐设备,根据它的原理设计了图2的机械设备,磨盘半径,把手,点O,M,Q成一直线,用长为的连杆将点Q与动力装置P相连(大小可变),点P在轨道上滑动并带动磨盘绕点O转动,.
(1)点P与点O之间距离的取值范围是_______.
(2)若磨盘转动500周,则点P在轨道上滑动的路径长为__________m.
15.如图,在中,.将绕的中点D旋转得,连接,则的最大值为_________.
三、解答题
16.如图,,,求的度数.
17.如图,DE为的直径,A为ED的延长线上点,过点A的一条直线交于B,C两点,已知,,求的度数.
18.如图,已知等边△ABC 的边长为8,点 P 是 AB 边上的一个动点(与点 A、B 不重合).直线 l 是经过点 P 的一条直线,把△ABC 沿直线 l 折叠,点 B 的对应点是点B'.当 PB=6 时,在直线 l 变化过程中,求△ACB'面积的最大值.
19.如图,在矩形中,,,点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动.
(1)几秒钟后的面积等于;
(2)在运动过程中,是否存在这样的时刻,使点恰好落在以点为圆心,为半径的圆上?若存在,求出运动时间;若不存在,请说明理由.
(3)在点、的运动过程中,几秒后是直角三角形?请直接写出答案.
20.对于平面直角坐标系中的图形,,给出如下定义:为图形上任意一点,为图形上任意一点,如果线段的长度有最小值,那么称这个最小值为图形,的“近距”,记作;如果线段的长度有最大值,那么称这个最大值为图形,的“远距”,记作.
已知点,.
(1)(点,线段)______,(点,线段)______;
(2)一次函数的图象与轴交于点,与轴交于点,若(线段,线段),
①求的值;
②直接写出(线段,线段)______;
(3)的圆心为,半径为1.若(线段),请直接写出(,线段)的取值范围.
21.已知:在中,,,将绕点顺时针旋转,点对应点为,点对应点为.设旋转过程中延长线与相交于点.
(1)如图所示,当点在边上时,请直接写出线段和线段之间的数量关系;
(2)当由图的位置旋转到图的位置时,试判断(1)中的结论是否成立,并说明理由;
(3)如图,若,设点为的中点,连接,将绕点旋转一周,直接写出的最大值与最小值.
22.将等边三角形如图放置在平面直角坐标系中,,为线段的中点,将线段绕点逆时针旋转60°得线段,连接.
(Ⅰ)如图1,求点的坐标;
(Ⅱ)在图1中,与交于点,连接,为的中点,连接,求线段的长.请你补全图形,并完成计算;
(Ⅲ)如图2,将绕点逆时针旋转,为线段的中点,为线段的中点,连接,请直接写出在旋转过程中的取值范围.
23.如图,抛物线与x轴交于两点,与y轴交于点C,直线与该抛物线交于两点.
(1)求抛物线的表达式.
(2)P是直线下方抛物线上的一个动点,作于点H,求的最大值.
(3)以点C为圆心,1为半径作圆,上是否存在点D,使得是以为直角边的直角三角形?若存在直接写出点D的坐标;若不存在,则说明理由.
【参考答案】
1.D 2.C 3.C 4.B 5.B 6.B 7.B 8.B 9.D 10.A
11.2.5
12. 0
13.3.
14.100cm≤OP≤170cm 900m
15.
16.28°
17.26°
18.
19.(1)2秒或4秒;(2)存在,时间为秒;(3)0秒或秒或6秒
20.(1)3,5;(2)①; ②;(3)(,线段).
21.(1);(2)依然成立;(3)的最大值为,最小值为.
22.(Ⅰ);(Ⅱ);(Ⅲ)
23.(1);(2) ;(3)存在,点D的坐标为 或 或
(1,-3)或
一、选择题
1.已知是直径为10的圆的一条弦,则的长度不可能是( )
A.2 B.5 C.9 D.11
2.若一个圆的半径为,那么该圆的面积等于( )
A. B. C. D.
3.如图,以O为圆心的两个圆中,大圆的半径分别交小圆于点C,D,连结,下列选项中不一定正确的是( )
A. B. C. D.
4.如图,正方形ABCD的顶点A、B在⊙O上,顶点C、D在⊙O内,将正方形ABCD绕点B顺时针旋转α度,使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等,则旋转角度α等于( )
A.36° B.30° C.25° D.22.5°
5.如图,在中,,则的角度是( )
A. B. C. D.
6.如图,⊙M的半径为2,圆心M的坐标为,点P是⊙M上的任意一点,PA⊥PB,且PA、PB与轴分别交于A、B两点,若点A、点B关于原点O对称,则AB的最大值为( )
A.3 B.14 C.6 D.8
7.如图,两个同心圆中有两条互相垂直的直径,其中大圆的半径是2,则图中阴影部分的面积是( )
A. B. C. D.
8.如图所示,在⊙O中,点A,O,D以及点B,O,C分别在一条直线上,则图中的弦有( )
A.2条 B.3条 C.4条 D.5条
9.如图,如图,的半径为2,圆心的坐标为,点是上的任意一点,,,与x轴分别交于A,B两点,若点A、点B关于原点O对称,则的最小值为( )
A.3 B.4 C.5 D.6
10.如图,函数的图象与x轴交于A,B两点,点C是以为圆心,2为半径的圆上的动点,P是的中点,连结,则线段的最小值是( )
A.1 B. C.2 D.
二、填空题
11.圆外一点到圆的最大距离为9cm,最小距离为4cm,则圆的半径是_____cm.
12.已知P为⊙O外的一点,P到⊙O上的点的最大距离为6,最小距离为2.若AB为⊙O内一条长为1的弦,则点P到AB的距离的最大值为_____,最小值为_____.
13.如图,平面直角坐标系中,点的坐标是,点是上一点,的半径为2,连接,则线段OB的最小值为__________.
14.图1是传统的手工磨豆腐设备,根据它的原理设计了图2的机械设备,磨盘半径,把手,点O,M,Q成一直线,用长为的连杆将点Q与动力装置P相连(大小可变),点P在轨道上滑动并带动磨盘绕点O转动,.
(1)点P与点O之间距离的取值范围是_______.
(2)若磨盘转动500周,则点P在轨道上滑动的路径长为__________m.
15.如图,在中,.将绕的中点D旋转得,连接,则的最大值为_________.
三、解答题
16.如图,,,求的度数.
17.如图,DE为的直径,A为ED的延长线上点,过点A的一条直线交于B,C两点,已知,,求的度数.
18.如图,已知等边△ABC 的边长为8,点 P 是 AB 边上的一个动点(与点 A、B 不重合).直线 l 是经过点 P 的一条直线,把△ABC 沿直线 l 折叠,点 B 的对应点是点B'.当 PB=6 时,在直线 l 变化过程中,求△ACB'面积的最大值.
19.如图,在矩形中,,,点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动.
(1)几秒钟后的面积等于;
(2)在运动过程中,是否存在这样的时刻,使点恰好落在以点为圆心,为半径的圆上?若存在,求出运动时间;若不存在,请说明理由.
(3)在点、的运动过程中,几秒后是直角三角形?请直接写出答案.
20.对于平面直角坐标系中的图形,,给出如下定义:为图形上任意一点,为图形上任意一点,如果线段的长度有最小值,那么称这个最小值为图形,的“近距”,记作;如果线段的长度有最大值,那么称这个最大值为图形,的“远距”,记作.
已知点,.
(1)(点,线段)______,(点,线段)______;
(2)一次函数的图象与轴交于点,与轴交于点,若(线段,线段),
①求的值;
②直接写出(线段,线段)______;
(3)的圆心为,半径为1.若(线段),请直接写出(,线段)的取值范围.
21.已知:在中,,,将绕点顺时针旋转,点对应点为,点对应点为.设旋转过程中延长线与相交于点.
(1)如图所示,当点在边上时,请直接写出线段和线段之间的数量关系;
(2)当由图的位置旋转到图的位置时,试判断(1)中的结论是否成立,并说明理由;
(3)如图,若,设点为的中点,连接,将绕点旋转一周,直接写出的最大值与最小值.
22.将等边三角形如图放置在平面直角坐标系中,,为线段的中点,将线段绕点逆时针旋转60°得线段,连接.
(Ⅰ)如图1,求点的坐标;
(Ⅱ)在图1中,与交于点,连接,为的中点,连接,求线段的长.请你补全图形,并完成计算;
(Ⅲ)如图2,将绕点逆时针旋转,为线段的中点,为线段的中点,连接,请直接写出在旋转过程中的取值范围.
23.如图,抛物线与x轴交于两点,与y轴交于点C,直线与该抛物线交于两点.
(1)求抛物线的表达式.
(2)P是直线下方抛物线上的一个动点,作于点H,求的最大值.
(3)以点C为圆心,1为半径作圆,上是否存在点D,使得是以为直角边的直角三角形?若存在直接写出点D的坐标;若不存在,则说明理由.
【参考答案】
1.D 2.C 3.C 4.B 5.B 6.B 7.B 8.B 9.D 10.A
11.2.5
12. 0
13.3.
14.100cm≤OP≤170cm 900m
15.
16.28°
17.26°
18.
19.(1)2秒或4秒;(2)存在,时间为秒;(3)0秒或秒或6秒
20.(1)3,5;(2)①; ②;(3)(,线段).
21.(1);(2)依然成立;(3)的最大值为,最小值为.
22.(Ⅰ);(Ⅱ);(Ⅲ)
23.(1);(2) ;(3)存在,点D的坐标为 或 或
(1,-3)或
同课章节目录
