2021-2022学年人教版九年级数学下册26.1 反比例函数 同步测试题(Word版含简答)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册26.1 反比例函数 同步测试题(Word版含简答) |  | |
| 格式 | docx | ||
| 文件大小 | 182.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 14:37:28 | ||
图片预览

文档简介
26.1 反比例函数 同步测试题
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
1. 下列函数中,与的反比例函数是( )
A. B. C. D.
2. 已知反比例函数,当时,,那么的值是( )
A. B. C. D.
3. 已知反比例函数的图象经过点,则这个函数的图象位于( )
A.第二、三象限 B.第一、三象限 C.第三、四象限 D.第二、四象限
4. 下列图象中,是函数的图象是( )
A. B.
C. D.
5. 反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象
6. 对于反比例函数,下列说法正确的是( )
A.图象经过点 B.图象位于第一、三象限
C.图象是中心对称图形 D.当时,随的增大而减小
7. 如图,在平面直角坐标系中,矩形对角线的交点与原点重合,顶点、在轴上,且,则过点的反比例函数的值为( )
A. B. C. D.
8. 已知双曲线,的部分图象如图所示,是轴正半轴上一点,过点作轴,分别交两个图象于点、.若,则的值为( )
A. B. C. D.
9. 边长为的正方形的对称中心是坐标原点,轴,轴,反比例函数与的图象均与正方形的边相交,则图中的阴影部分的面积是( )
A. B. C. D.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
10. 若关于、的函数是反比例函数,则________.
11. 已知与成反比例,且当时,,则当时,________.
12. 如果函数是反比例函数,那么________.
13. 如图,点是反比例函数图像上的一点,轴于点,的面积为.若点也在此函数的图像上,则________.
14. 已知反比例函数,点,是函数图象上两点,且满足,则的值为________.
15. 如图,在平面直角坐标系中,点和点分别在轴和轴正半轴上,以、为边作矩形,双曲线交于点,.则矩形的面积是________.
16. 在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度(单位:)与体积(单位:)满足函数关系式为常数,其图象如图所示,则的值为________.
17. 如图,点和点都在反比例函数的图象上,若=,,则的值是________.
18. 如图,在平面直角坐标系中,过点分别作轴、轴的垂线与反比例函数的图象交于两点,则四边形的面积为________.
三、 解答题 (本题共计 7 小题 ,共计66分 , )
19. 已知与成反比例,且当时,,求与之间的函数关系式.
20. 已知反比例函数的图象的一支位于第一象限.
(1)图象的另一支位于哪个象限?常数的取值范围是什么?
(2)在这个函数图象上任取点和,如果,那么与有怎样的大小关系?
21. 如图是双曲线、在第一象限的图象,,过上的任意一点,作轴的平行线交于,交轴于,若,求双曲线的解析式.
22. 如图,在平面直角坐标系中,直线经过原点,且与反比例函数图象交于点,点.分别过、作轴于,轴于,再以、为半径作和.
(1)求反比例函数的解析式及的值;
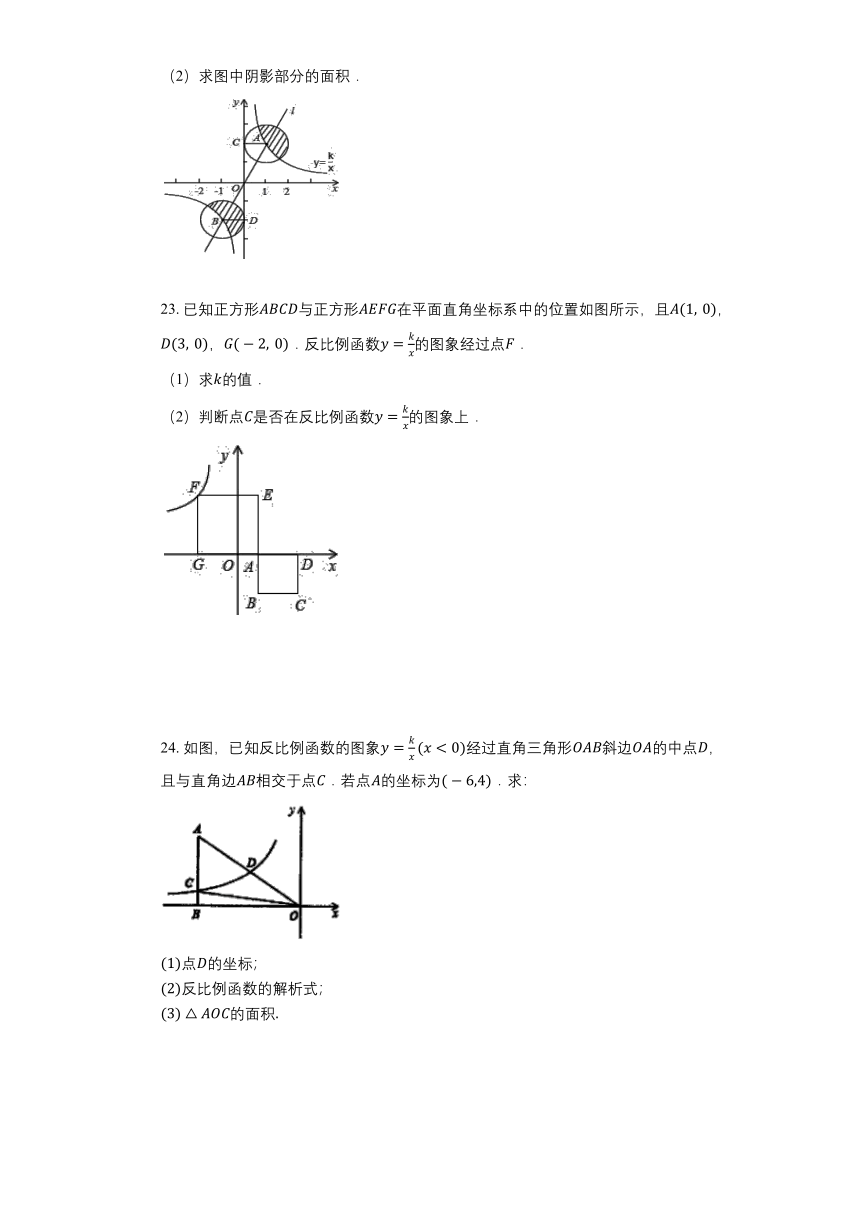
(2)求图中阴影部分的面积.
23. 已知正方形与正方形在平面直角坐标系中的位置如图所示,且,,.反比例函数的图象经过点.
(1)求的值.
(2)判断点是否在反比例函数的图象上.
24. 如图,已知反比例函数的图象经过直角三角形斜边的中点,且与直角边相交于点.若点的坐标为.求:
点的坐标;
反比例函数的解析式;
的面积
25. 如图,已知双曲线经过点,点是双曲线第三象限上的动点,过作轴,过作轴,垂足分别为,,连接,.
求的值;
若的面积为,求直线的解析式;
判断与的位置关系,并说明理由.
参考答案
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
1.D
2.A
3.D
4.B
5.C
6.C
7.B
8.D
9.A
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
10.
11.
12.
13.
14.
15.
16.
17.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:设,
把,代入得,
所以,
所以与之间的函数关系式为.
20.
【答案】
解:(1)∵ 反比例函数的图象的一支位于第一象限,
∴ 图象的另一支位于第三象限,且,解得
∴ 的取值范围为;
(2)由(1)可知该反比例函数在每个象限内,随的增大而减小,
当、两点在同一象限内时,
∵ ,
∴ ,
当、两点不在同一象限内,
∵ ,
∴ 点在第一象限,点在第三象限,
∴ .
21.
【答案】
解:设双曲线的解析式为,
由题意得:,
,
解得;;
则双曲线的解析式为.
22.
【答案】
解:(1)∵ 点在图象上,
∴
∴
∵
∴
(2)∵
∴ 根据中心对称性
23.
【答案】
解:(1)∵ 点,,
∴ ,
∵ 四边形是正方形,
∴ ,
∵ 点在反比例函数的图象上,
∴ ;
(2)∵ ,,
∴ ,
∴ ,
∴ ,
∴ 点在反比例函数的图象上.
24.
【答案】
解:过点作轴.
∵ 是直角三角形,
∴ ,
∴ ,
∴ .
又∵ 为的中点,
∴ .
,,
∴
∴ .
∵ 曲线过,
∴ ,
解得,
∴ 反比例函数解析式为.
∵ 交反比例函数图象于点,
∴ 点的横坐标为.
当时, ,
∴ ,
∴
.
25.
【答案】
解:∵ 双曲线经过点,
∴ ,
解得.
设点到的距离为.
∵ ,且轴,
∴ ,
∴ ,
解得.
∵ 点是双曲线第三象限上的动点,点的纵坐标为,
∴ 点的纵坐标为,
∴ 可得,解得,
∴ 点的坐标为.
设直线的解析式为,
则
解得
故直线的解析式为.
.理由如下:
∵ 轴,轴,
∴ 设点的坐标为,
又点的坐标为,
∴ 点,的坐标分别为,,
设直线的解析式为,
则
解得
故直线的解析式为.
设直线的解析式为,
则
解得
故直线的解析式为.
∵ 直线,的解析式的斜率都为,
∴ 与的位置关系是.试卷第2页,总2页
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
1. 下列函数中,与的反比例函数是( )
A. B. C. D.
2. 已知反比例函数,当时,,那么的值是( )
A. B. C. D.
3. 已知反比例函数的图象经过点,则这个函数的图象位于( )
A.第二、三象限 B.第一、三象限 C.第三、四象限 D.第二、四象限
4. 下列图象中,是函数的图象是( )
A. B.
C. D.
5. 反比例函数的图象在( )
A.第一、二象限 B.第一、三象限 C.第二、四象限 D.第三、四象
6. 对于反比例函数,下列说法正确的是( )
A.图象经过点 B.图象位于第一、三象限
C.图象是中心对称图形 D.当时,随的增大而减小
7. 如图,在平面直角坐标系中,矩形对角线的交点与原点重合,顶点、在轴上,且,则过点的反比例函数的值为( )
A. B. C. D.
8. 已知双曲线,的部分图象如图所示,是轴正半轴上一点,过点作轴,分别交两个图象于点、.若,则的值为( )
A. B. C. D.
9. 边长为的正方形的对称中心是坐标原点,轴,轴,反比例函数与的图象均与正方形的边相交,则图中的阴影部分的面积是( )
A. B. C. D.
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 , )
10. 若关于、的函数是反比例函数,则________.
11. 已知与成反比例,且当时,,则当时,________.
12. 如果函数是反比例函数,那么________.
13. 如图,点是反比例函数图像上的一点,轴于点,的面积为.若点也在此函数的图像上,则________.
14. 已知反比例函数,点,是函数图象上两点,且满足,则的值为________.
15. 如图,在平面直角坐标系中,点和点分别在轴和轴正半轴上,以、为边作矩形,双曲线交于点,.则矩形的面积是________.
16. 在一个可以改变体积的密闭容器内装有一定质量的某种气体,当改变容器的体积时,气体的密度也会随之改变,密度(单位:)与体积(单位:)满足函数关系式为常数,其图象如图所示,则的值为________.
17. 如图,点和点都在反比例函数的图象上,若=,,则的值是________.
18. 如图,在平面直角坐标系中,过点分别作轴、轴的垂线与反比例函数的图象交于两点,则四边形的面积为________.
三、 解答题 (本题共计 7 小题 ,共计66分 , )
19. 已知与成反比例,且当时,,求与之间的函数关系式.
20. 已知反比例函数的图象的一支位于第一象限.
(1)图象的另一支位于哪个象限?常数的取值范围是什么?
(2)在这个函数图象上任取点和,如果,那么与有怎样的大小关系?
21. 如图是双曲线、在第一象限的图象,,过上的任意一点,作轴的平行线交于,交轴于,若,求双曲线的解析式.
22. 如图,在平面直角坐标系中,直线经过原点,且与反比例函数图象交于点,点.分别过、作轴于,轴于,再以、为半径作和.
(1)求反比例函数的解析式及的值;
(2)求图中阴影部分的面积.
23. 已知正方形与正方形在平面直角坐标系中的位置如图所示,且,,.反比例函数的图象经过点.
(1)求的值.
(2)判断点是否在反比例函数的图象上.
24. 如图,已知反比例函数的图象经过直角三角形斜边的中点,且与直角边相交于点.若点的坐标为.求:
点的坐标;
反比例函数的解析式;
的面积
25. 如图,已知双曲线经过点,点是双曲线第三象限上的动点,过作轴,过作轴,垂足分别为,,连接,.
求的值;
若的面积为,求直线的解析式;
判断与的位置关系,并说明理由.
参考答案
一、 选择题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
1.D
2.A
3.D
4.B
5.C
6.C
7.B
8.D
9.A
二、 填空题 (本题共计 9 小题 ,每题 3 分 ,共计27分 )
10.
11.
12.
13.
14.
15.
16.
17.
三、 解答题 (本题共计 7 小题 ,每题 10 分 ,共计70分 )
19.
【答案】
解:设,
把,代入得,
所以,
所以与之间的函数关系式为.
20.
【答案】
解:(1)∵ 反比例函数的图象的一支位于第一象限,
∴ 图象的另一支位于第三象限,且,解得
∴ 的取值范围为;
(2)由(1)可知该反比例函数在每个象限内,随的增大而减小,
当、两点在同一象限内时,
∵ ,
∴ ,
当、两点不在同一象限内,
∵ ,
∴ 点在第一象限,点在第三象限,
∴ .
21.
【答案】
解:设双曲线的解析式为,
由题意得:,
,
解得;;
则双曲线的解析式为.
22.
【答案】
解:(1)∵ 点在图象上,
∴
∴
∵
∴
(2)∵
∴ 根据中心对称性
23.
【答案】
解:(1)∵ 点,,
∴ ,
∵ 四边形是正方形,
∴ ,
∵ 点在反比例函数的图象上,
∴ ;
(2)∵ ,,
∴ ,
∴ ,
∴ ,
∴ 点在反比例函数的图象上.
24.
【答案】
解:过点作轴.
∵ 是直角三角形,
∴ ,
∴ ,
∴ .
又∵ 为的中点,
∴ .
,,
∴
∴ .
∵ 曲线过,
∴ ,
解得,
∴ 反比例函数解析式为.
∵ 交反比例函数图象于点,
∴ 点的横坐标为.
当时, ,
∴ ,
∴
.
25.
【答案】
解:∵ 双曲线经过点,
∴ ,
解得.
设点到的距离为.
∵ ,且轴,
∴ ,
∴ ,
解得.
∵ 点是双曲线第三象限上的动点,点的纵坐标为,
∴ 点的纵坐标为,
∴ 可得,解得,
∴ 点的坐标为.
设直线的解析式为,
则
解得
故直线的解析式为.
.理由如下:
∵ 轴,轴,
∴ 设点的坐标为,
又点的坐标为,
∴ 点,的坐标分别为,,
设直线的解析式为,
则
解得
故直线的解析式为.
设直线的解析式为,
则
解得
故直线的解析式为.
∵ 直线,的解析式的斜率都为,
∴ 与的位置关系是.试卷第2页,总2页
