3.1.1椭圆及其标准方程课件 -2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共27张PPT)
文档属性
| 名称 | 3.1.1椭圆及其标准方程课件 -2021-2022学年高二上学期数学人教A版(2019)选择性必修第一册(共27张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 22:08:06 | ||
图片预览







文档简介
(共27张PPT)
第三章:圆锥曲线与方程
椭圆及其标准方程
一、引入:
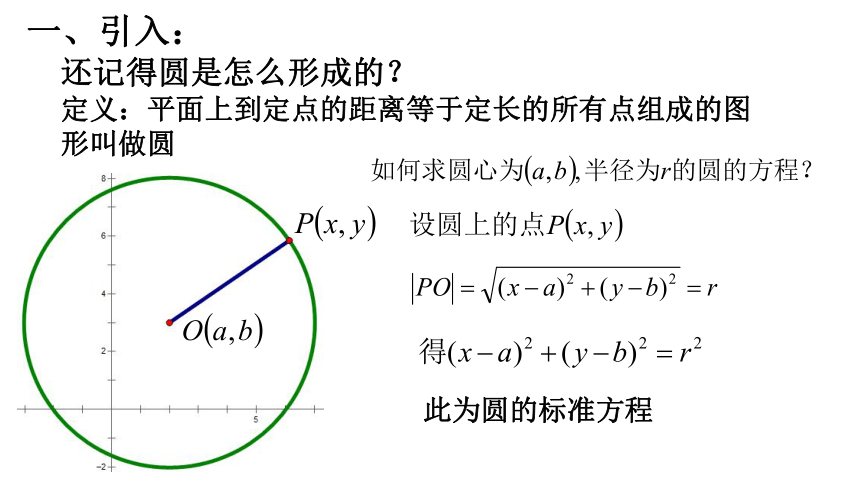
还记得圆是怎么形成的?
定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆
此为圆的标准方程
1.下面请三位同学上讲台进行实验
2.再用几何画板展示
三、椭圆的定义:
思考:
如果把上面括号处改为等于或小于会怎么样呢?
三、椭圆的标准方程的推导:
复习:求轨迹方程的一般步骤:
第一步:建立适当的直角坐标系
(使得图形越对称越好)
第二步:设点
第三步:列式
第四步:化简
三、椭圆的标准方程的推导:
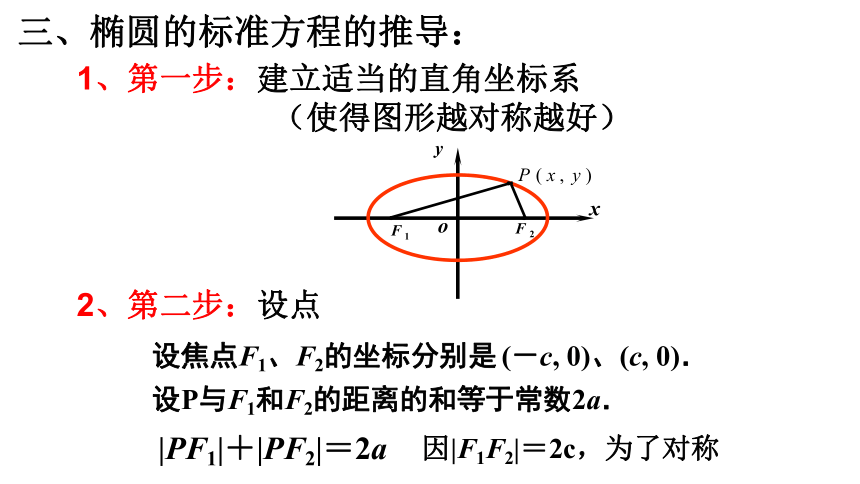
1、第一步:建立适当的直角坐标系
(使得图形越对称越好)
设焦点F1、F2的坐标分别是 (-c, 0)、(c, 0).
设P与F1和F2的距离的和等于常数2a.
|PF1|+|PF2|=2a
因|F1F2|=2c,为了对称
2、第二步:设点
三、椭圆的标准方程的推导:
3、第三步:列式
(-c, 0)
(c, 0)
|PF1|+|PF2|=2a
三、椭圆的标准方程的推导:
4、第四步:化简
移项:
平方:
移项化简:
再平方:
整理得:
两边同除以 得:
只有一个根式,将它放在方程的一边,其他项移到另一边,再平方
有两个根式,将它们分散,放到方程的两边,一边一个根式,再平方
4、第四步:化简
三、椭圆的标准方程的推导:
令
,得
为了方便我们
问:
如何根据标准方程判断焦点在哪个坐标轴上?
椭圆的方程
椭圆的标准方程
分母哪个大,焦点就在哪一坐标轴上
类比
椭圆的标准方程
定义
图形
方程
焦点
a、b、c之间的关系
|PF1|+|PF2|=2a (2a>|F1F2|)
(c,0)、( c,0)
(0,c)、(0, c)
分母哪个大,焦点就在哪一坐标轴上
练习1 下列方程哪些表示椭圆?
在 x 轴上,(-3,0)和(3,0)
在 y 轴上,(0,-5)和(0,5)
在y 轴上,(0,-1)和(0,1)
练习2、判定下列椭圆的焦点在 哪个轴上,写出焦点坐标
在y 轴上, 和
练习3:
若方程 表示椭圆,求n的取值范围
x
y
O
F1
F2
这是定义法,还有其他方法?
四、例题精解
方法二:待定系数法
由 得:
四、例题精解
例2 :如图,在 圆上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
解:设
未知的这样设:
已知的这样设:
用未知表示已知:
四、例题精解
例3:如图,设A,B的坐标分别(-5,0),(5,0) 直线AM,BM相交于点M,且它们的斜率之积为 ,
求点M的轨迹方程.
解:设点M(x,y)
点M的轨迹方程
四、例题精解
五、课堂练习
3、求满足下面条件的椭圆的标准方程
有更快的方法:凡是不知道焦点在哪,经过两个已知点的椭圆都可以这样做
联立
高考链接
2017全国I卷理科20题
解得
...............................4分
求椭圆轨迹方程的热点:
课堂小结
今天是15号,请座位号是15的同学总结今天所学
1.用待定系数法求椭圆的标准方程时,若已知焦点的位置,可直接设出标准方程;若焦点位置不确定,可分两种情况求解;也可设为mx2+ny2=1(m>0,n>0,A≠B)求解.
2.解决与椭圆有关的轨迹问题时,要注意检验所得到的方程的解是否都在曲线上.
3.涉及椭圆的焦点三角形问题,可结合椭圆的定义列出|PF1|+|PF2|=2a求解,因此回归定义是求解椭圆的焦点三角形问题的常用方法.
作业
《椭圆的标准方程》学案
预习《椭圆的简单几何性质》
谢谢大家
第三章:圆锥曲线与方程
椭圆及其标准方程
一、引入:
还记得圆是怎么形成的?
定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆
此为圆的标准方程
1.下面请三位同学上讲台进行实验
2.再用几何画板展示
三、椭圆的定义:
思考:
如果把上面括号处改为等于或小于会怎么样呢?
三、椭圆的标准方程的推导:
复习:求轨迹方程的一般步骤:
第一步:建立适当的直角坐标系
(使得图形越对称越好)
第二步:设点
第三步:列式
第四步:化简
三、椭圆的标准方程的推导:
1、第一步:建立适当的直角坐标系
(使得图形越对称越好)
设焦点F1、F2的坐标分别是 (-c, 0)、(c, 0).
设P与F1和F2的距离的和等于常数2a.
|PF1|+|PF2|=2a
因|F1F2|=2c,为了对称
2、第二步:设点
三、椭圆的标准方程的推导:
3、第三步:列式
(-c, 0)
(c, 0)
|PF1|+|PF2|=2a
三、椭圆的标准方程的推导:
4、第四步:化简
移项:
平方:
移项化简:
再平方:
整理得:
两边同除以 得:
只有一个根式,将它放在方程的一边,其他项移到另一边,再平方
有两个根式,将它们分散,放到方程的两边,一边一个根式,再平方
4、第四步:化简
三、椭圆的标准方程的推导:
令
,得
为了方便我们
问:
如何根据标准方程判断焦点在哪个坐标轴上?
椭圆的方程
椭圆的标准方程
分母哪个大,焦点就在哪一坐标轴上
类比
椭圆的标准方程
定义
图形
方程
焦点
a、b、c之间的关系
|PF1|+|PF2|=2a (2a>|F1F2|)
(c,0)、( c,0)
(0,c)、(0, c)
分母哪个大,焦点就在哪一坐标轴上
练习1 下列方程哪些表示椭圆?
在 x 轴上,(-3,0)和(3,0)
在 y 轴上,(0,-5)和(0,5)
在y 轴上,(0,-1)和(0,1)
练习2、判定下列椭圆的焦点在 哪个轴上,写出焦点坐标
在y 轴上, 和
练习3:
若方程 表示椭圆,求n的取值范围
x
y
O
F1
F2
这是定义法,还有其他方法?
四、例题精解
方法二:待定系数法
由 得:
四、例题精解
例2 :如图,在 圆上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是什么?为什么?
解:设
未知的这样设:
已知的这样设:
用未知表示已知:
四、例题精解
例3:如图,设A,B的坐标分别(-5,0),(5,0) 直线AM,BM相交于点M,且它们的斜率之积为 ,
求点M的轨迹方程.
解:设点M(x,y)
点M的轨迹方程
四、例题精解
五、课堂练习
3、求满足下面条件的椭圆的标准方程
有更快的方法:凡是不知道焦点在哪,经过两个已知点的椭圆都可以这样做
联立
高考链接
2017全国I卷理科20题
解得
...............................4分
求椭圆轨迹方程的热点:
课堂小结
今天是15号,请座位号是15的同学总结今天所学
1.用待定系数法求椭圆的标准方程时,若已知焦点的位置,可直接设出标准方程;若焦点位置不确定,可分两种情况求解;也可设为mx2+ny2=1(m>0,n>0,A≠B)求解.
2.解决与椭圆有关的轨迹问题时,要注意检验所得到的方程的解是否都在曲线上.
3.涉及椭圆的焦点三角形问题,可结合椭圆的定义列出|PF1|+|PF2|=2a求解,因此回归定义是求解椭圆的焦点三角形问题的常用方法.
作业
《椭圆的标准方程》学案
预习《椭圆的简单几何性质》
谢谢大家
