图形的旋转

(共30张PPT)
一、生活情景
图形的旋转
在平面内，将一个图形绕一个定点按某一个方向（逆时针或顺时针方向）转动一定的角度，这样的变换叫做图形的旋转，这个定点叫做旋转中心，这个角叫做旋转角旋转后图形的位置是由旋转中心、旋转方向和旋转角确定的。
“一个图形绕着一个定点旋转一定角度”，意味着图形上每个点都同时按相同的方向旋转了相同的角度。
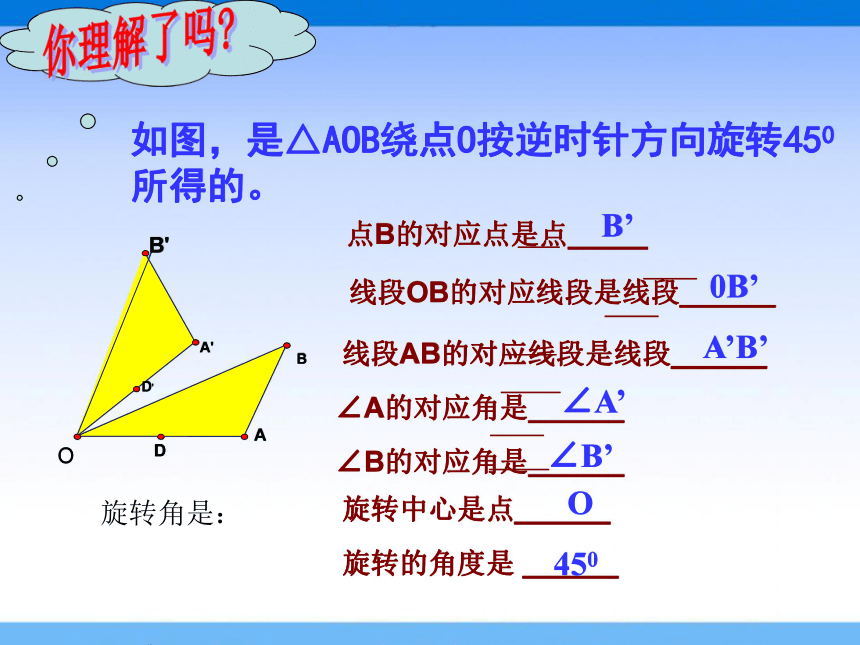
线段OB的对应线段是线段______
∠A的对应角是______
线段AB的对应线段是线段______
∠B的对应角是______
旋转中心是点______
旋转的角度是 ______
点B的对应点是点_____
如图，是△AOB绕点O按逆时针方向旋转450所得的。
B’
0B’
A’B’
∠A’
∠B’
O
450
D'
D
A'
A
B
O
B'
旋转角是：
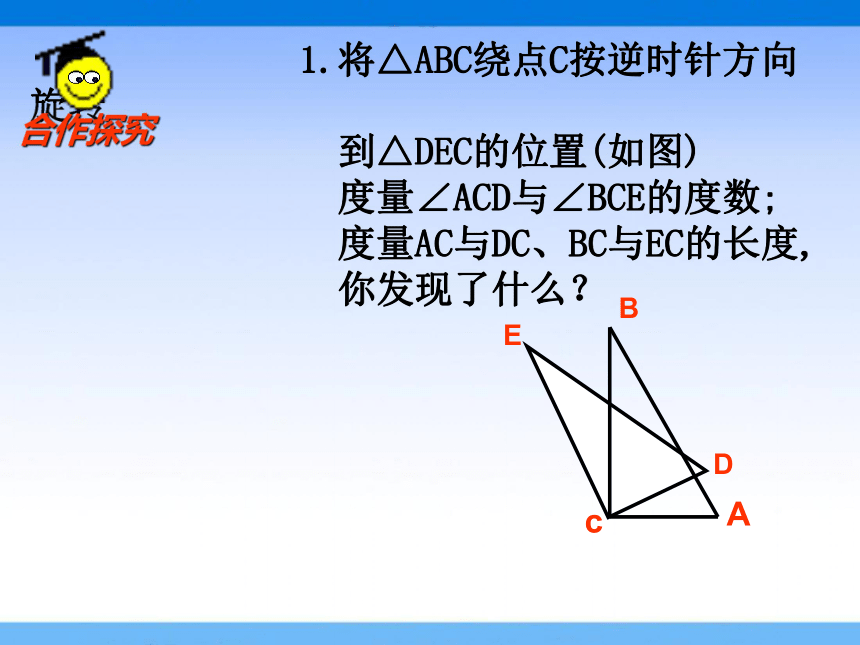
1.将△ABC绕点C按逆时针方向旋转
到△DEC的位置(如图)
度量∠ACD与∠BCE的度数;
度量AC与DC、BC与EC的长度,
你发现了什么？
合作探究
c
E
B
D
A
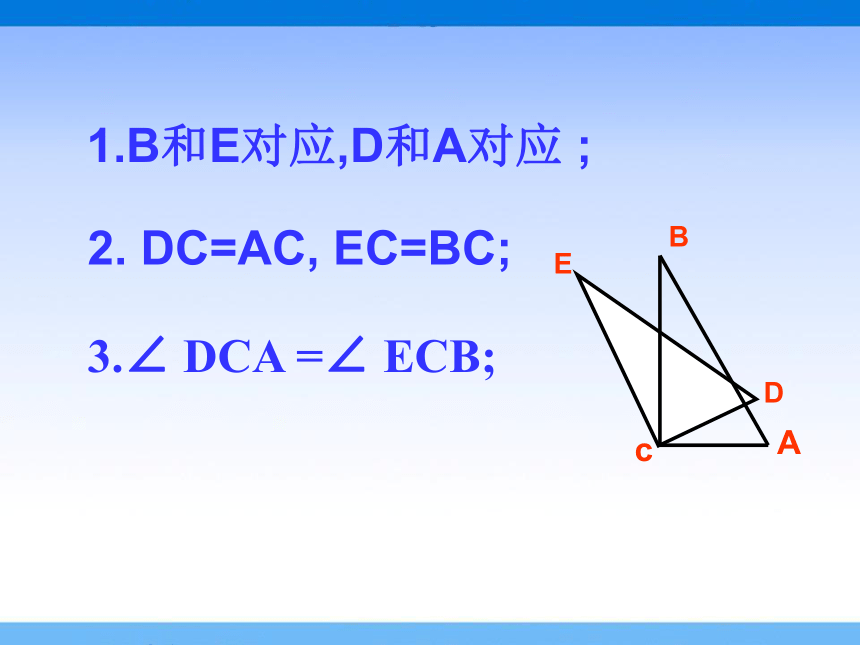
1.B和E对应,D和A对应 ;
2. DC=AC, EC=BC;
c
E
B
D
A
3.∠ DCA =∠ ECB;
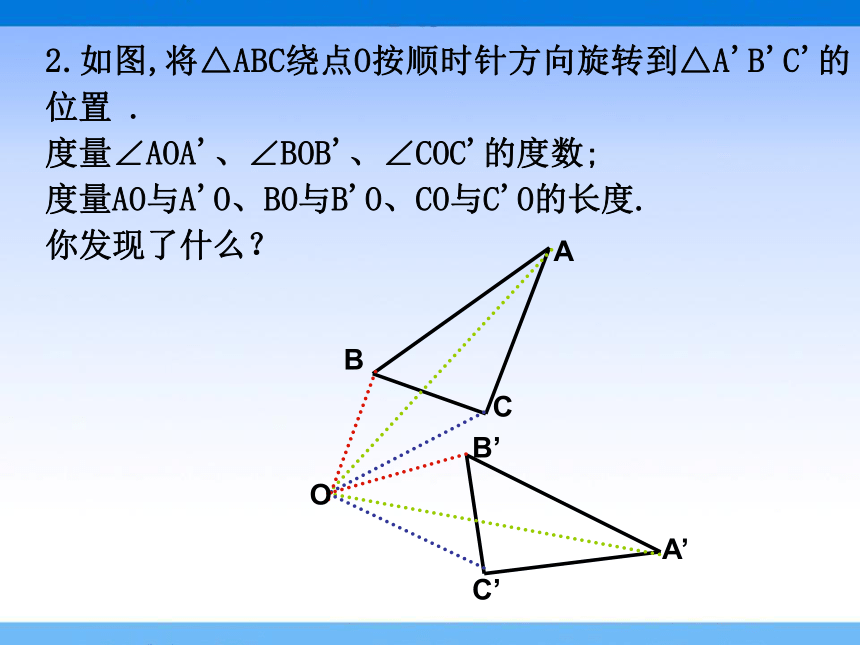
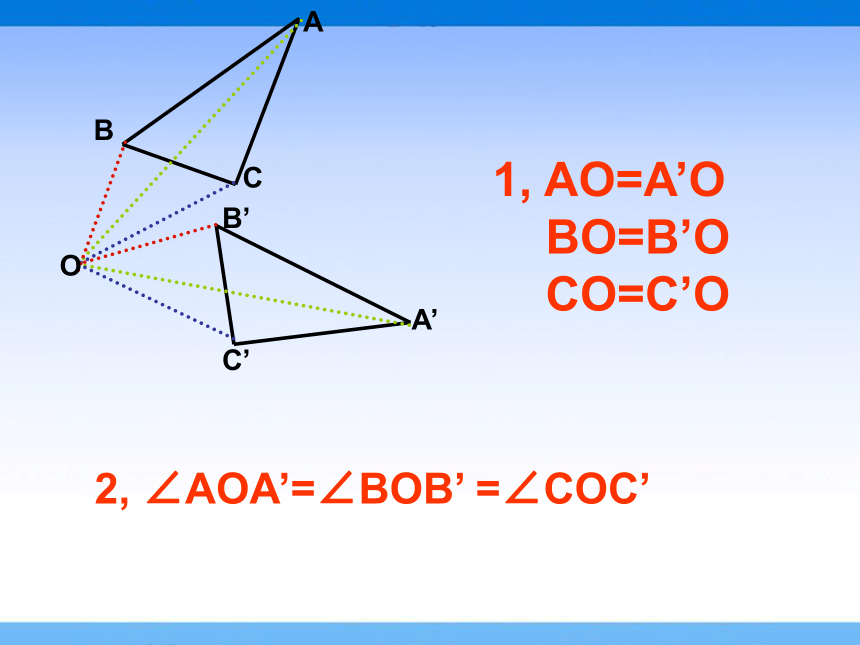
2.如图,将△ABC绕点O按顺时针方向旋转到△A'B'C'的位置 .
度量∠AOA'、∠BOB'、∠COC'的度数;
度量AO与A'O、BO与B'O、CO与C'O的长度.
你发现了什么？
O
B
C
A
B’
C’
A’
2, ∠AOA’=∠BOB’ =∠COC’
1, AO=A’O
BO=B’O
CO=C’O
O
B
C
A
B’
C’
A’
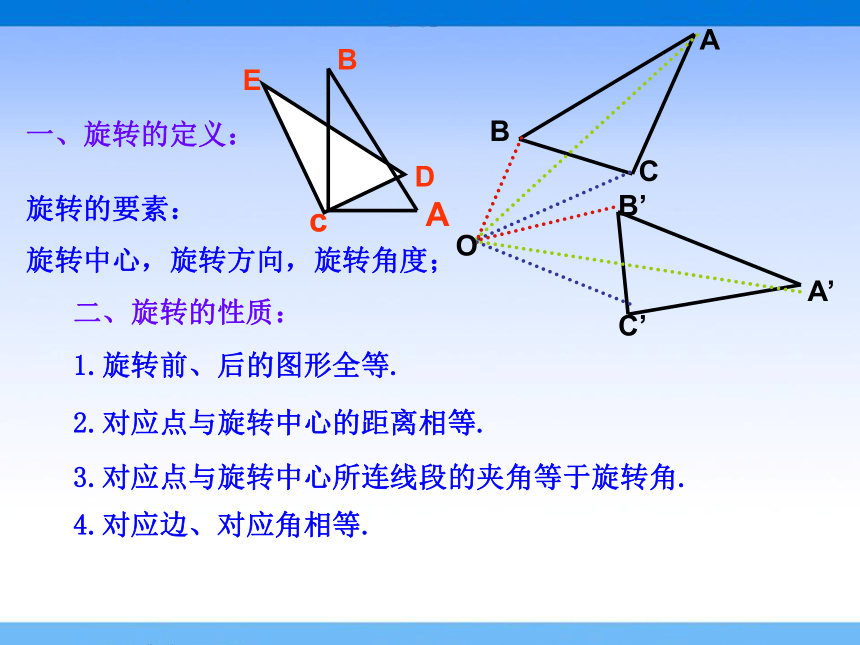
旋转的要素：
旋转中心，旋转方向，旋转角度；
1.旋转前、后的图形全等.
4.对应边、对应角相等.
一、旋转的定义：
二、旋转的性质：
2.对应点与旋转中心的距离相等.
3.对应点与旋转中心所连线段的夹角等于旋转角.
c
E
B
D
A
O
B
C
A
B’
C’
A’
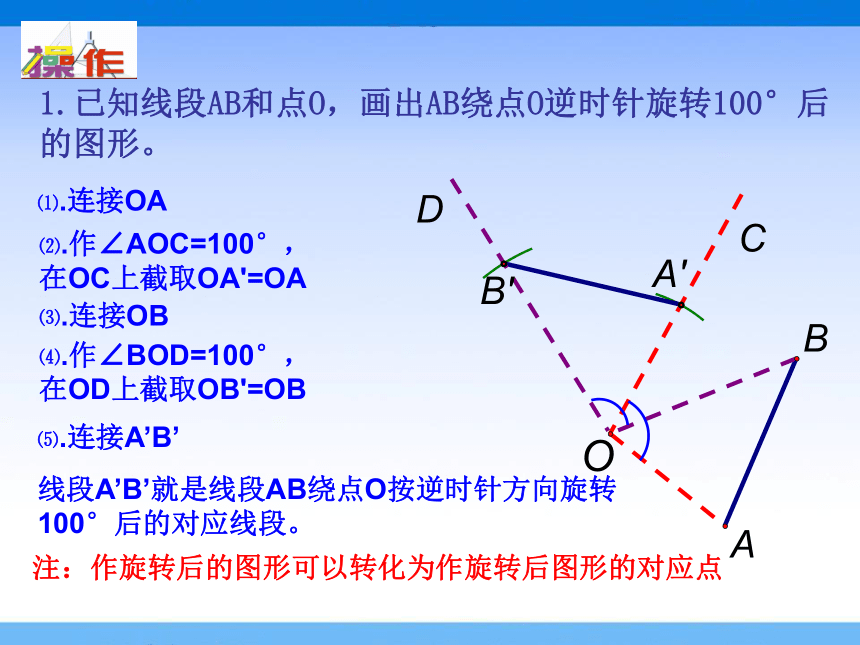
⑸.连接A’B’
线段A’B’就是线段AB绕点O按逆时针方向旋转100°后的对应线段。
A'
B'
B
A
O
D
C
1.已知线段AB和点O，画出AB绕点O逆时针旋转100°后的图形。
⑴.连接OA
⑵.作∠AOC=100°，在OC上截取OA'=OA
⑷.作∠BOD=100°，在OD上截取OB'=OB
⑶.连接OB
注：作旋转后的图形可以转化为作旋转后图形的对应点
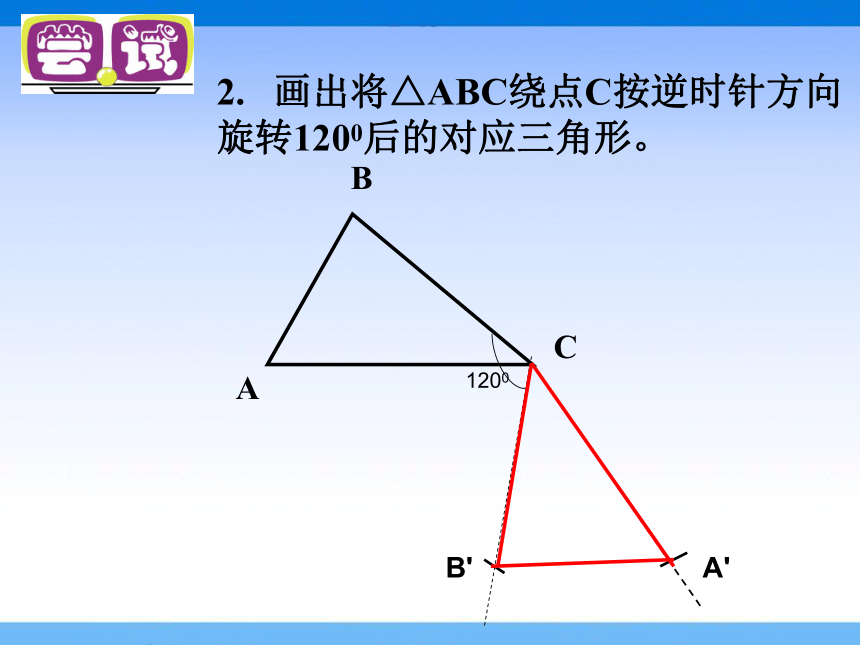
2. 画出将△ABC绕点C按逆时针方向旋转1200后的对应三角形。
A
B
C
B'
A'
1200
如图，△ABC是等边三角形，D是BC上一
点，△ABD经过旋转后到达△ACD’的位置。
（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）如果M是AB的中点，那么经过上述旋转后，点M转到了什么位置？
M'
M
D'
C
A
B
D
拓展应用：
下图是由正方形ABCD旋转而成。
（1）旋转中心是__________
(2) 旋转的角度是_________
点A
450
(3) 若正方形的边长是1，则C’D=_________
C'
D'
B'
B
A
C
D
　　在图中，正方形ABCD与正方形EFGH边长相等，这个图案可以看作是哪个“基本图案”通过旋转得到的．
知 识 讲 解
解析：（法1）整个图形可以看做是图形的八分之一(一组大小不等的三个“角”)绕中心位置，按照同一方向连续旋转45°、90°、135°、180°、225°、270°、315°，由前后的图形共同组成的.
解析：（法2）整个图形也可以看做是图形的四分之一(两组相邻的“角”)绕中心位置连续旋转90°、180°、270° ，由前后的图形共同组成的.
解析：（法3）整个图形还可以看做是图形的二分之一(四组相邻的“角”)绕中心位置旋转180°由前后的图形共同组成的.
【例1】你能作出 “将方格中的小旗子绕 O点按顺时针方向旋转90 ”后的图案吗？
例 题
在方格纸上作出 “小旗子”绕 O点按顺时针方向旋转90 后的图案 ，并简述理由.(让我们一起来）
O
A1
A
C
B
B1
C1
A
B
C
D
在旋转过程中,确定一个三角形旋转后的位置，除需要
原来的位置外，还需要什么条件？
E
(1)旋转方向
(2)旋转中心
(3)旋转角.
解析：
1、在下图中，将大写字母 N 绕它下侧的顶点按顺时针方向旋转 90 ，作出旋转后的图案.
跟踪训练
随 堂 练 习
1．（2010·益阳中考）小军将一个直角三角板（如图）绕它的一条直角边所在的直线旋转一周形成一个几何体，将这个几何体的侧面展开得到的大致图形是（ ）
Ａ． B． C． D．
D
2．（2010·徐州中考）如图，在6×4方格纸中，格点三角形甲经过旋转后得到格点三角形乙，则其旋转中心是
（ ）
A．点M B．格点N
C．格点P D．格点Q
B
3．（2010·淄博中考）如图，△A′B′C′是由△ABC经过变换得到的，则这个变换过程是( )
A.平移　　B.轴对称
C.旋转　 D.平移后再轴对称
C
B
A
B′
A′
C′
D
B（－1，2）
C（－2，－1）
D（1，－2）
（－b,a)
（－b,a)
(3，-2)
(-2，-3)
(-3，2)
(2，3）
将点(a,b)顺时针旋转90°，得到的点的坐标是（b,-a)
B2　
B1　
B1由点A绕原点顺时针旋转得到，故B1(1,3)
B2由点A绕原点逆时针旋转得到，故B2(-1,-3)