青岛版九年级下册数学第五章对函数的再探索5.5二次函数y=ax2的图象和性质
文档属性
| 名称 | 青岛版九年级下册数学第五章对函数的再探索5.5二次函数y=ax2的图象和性质 |  | |
| 格式 | zip | ||
| 文件大小 | 879.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-16 07:14:34 | ||
图片预览





文档简介
(共25张PPT)
y=kx+b (k≠0)
y= (k≠0)
问:1.如何画出函数图象呢
2.如何得到相应的性质呢
直线
双曲线
列表
——
描点
——
连线
(描点法)
→
观察图象
总结性质
y=ax2 (a≠0)
图象:
性质:
k
x
二次函数
请同学们用描点法按下列要求画图:
请A组同学同桌合作画函数y=x2的图象;
请B组同学同桌合作画函数y= x2的图象。
0
y
3
4
1
2
x
1
2
-1
-2
0
y
3
4
1
2
x
1
2
-1
-2
…
2
0
2
…
…
4
1
0
1
4
…
y=x2
…
2
1
0
-1
-2
…
x
y= x2
1
2
9
8
1
8
3
2
9
4
9
8
9
4
1
8
1
4
1
4
1
2
1
2
1
2
3
2
1
2
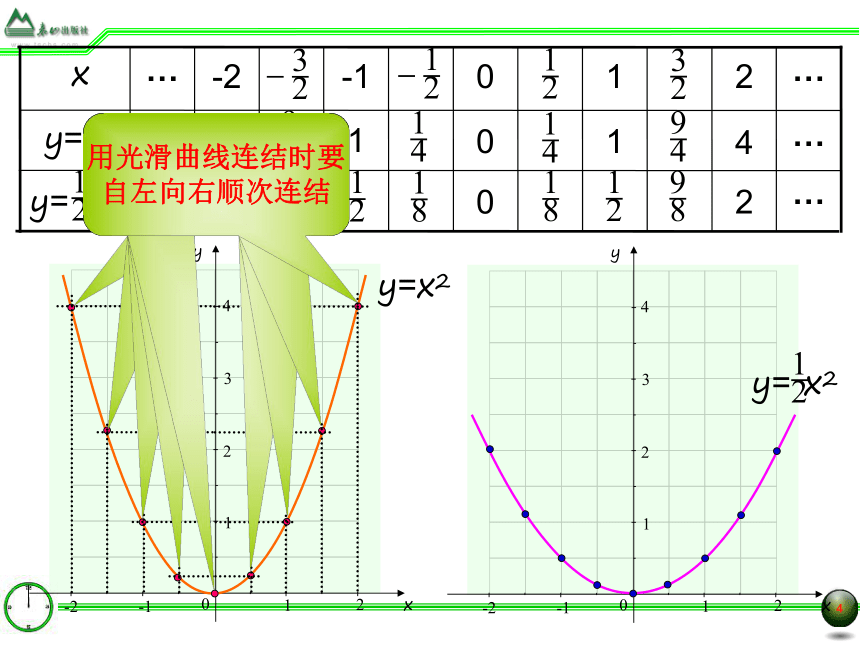
y=x2
y= x2
1
2
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
0
y
3
4
1
2
x
1
2
-1
-2
0
y
3
4
1
2
x
1
2
-1
-2
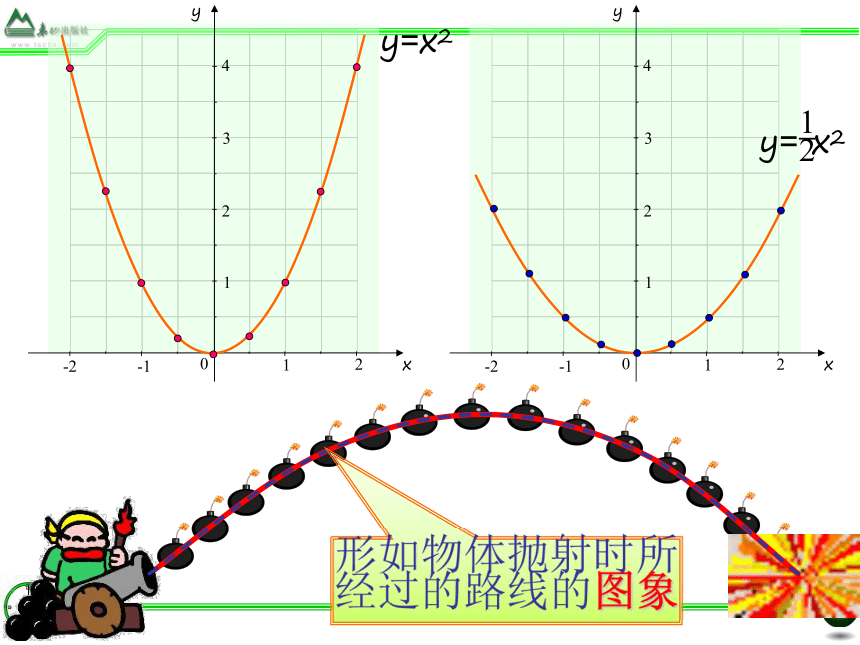
y= x2
1
2
y=x2
形如物体抛射时所经过的路线的图象
0
y
3
4
1
2
x
1
2
-1
-2
0
y
3
4
1
2
x
1
2
-1
-2
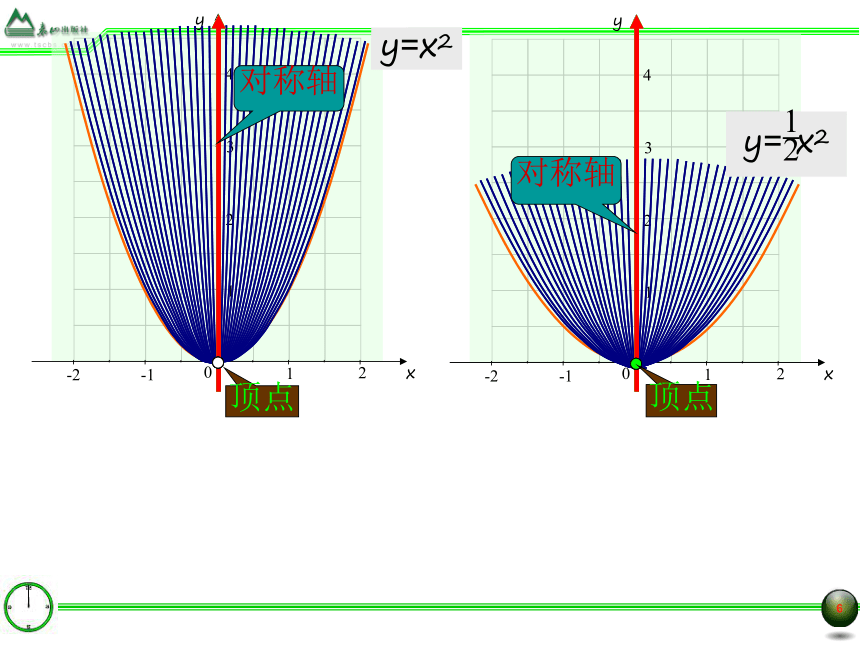
y=x2
y= x2
1
2
对称轴
对称轴
顶点
顶点
向上
y轴
(0,0)
最低
减小
增大
请同学们用描点法按下列要求画图:
请A组的同学同桌合作在和抛物线y=x2同一坐标系中画函数y=-x2的图象,并观察;
请B组同学同桌合作在和抛物线y= x2同一坐标系中画函数y=- x2的图象,并观察。
1
2
1
2
向下
原点
y轴
向上
原点
y轴
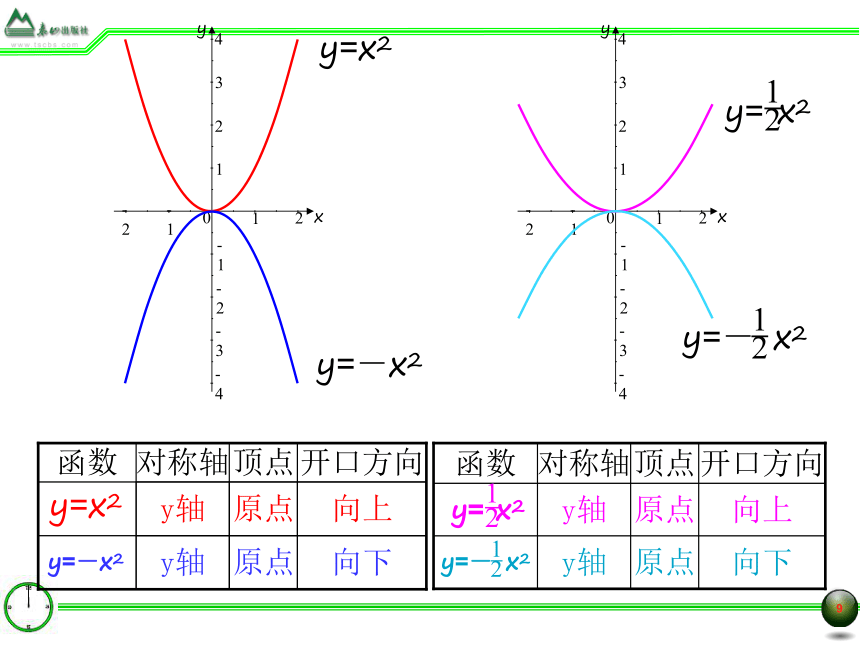
开口方向
顶点
对称轴
函数
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y=-x2
y=x2
y= x2
1
2
y=- x2
1
2
向下
原点
y轴
向上
原点
y轴
开口方向
顶点
对称轴
函数
y=x2
y=-x2
y= x2
1
2
y=- x2
1
2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y=-x2
y=x2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y= x2
1
2
y=- x2
1
2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y=-x2
y=x2
y= x2
1
2
y=- x2
1
2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y=-x2
y=x2
y= x2
1
2
y=- x2
1
2
y= x2
1
2
y=- x2
1
2
向下
y轴
(0,0)
最高
增大
减小
练习1:分别说出抛物线y=4x2与y=-5x2的开口方向,对称轴与顶点坐标。
巩固练习
练习2 :对于函数y=2x2,下列结论正确的是( ).
A.当x取任何实数时,y的值总是正的
B.x的值增大,y的值也随着增大
C.x的值增大,y的值随着减小
D.图像关于y轴对称
练习3 :如何根据函数的图象,
(1)根据图象,求当y=2时,对应的x的值(精确到0.1);
(2)利用图象,求的 值(精确到0.1)。
D
0
x
y
1
2
3
4
1
2
-1
-2
y=x2
-
练习5:观察上面画的图象回答:(1)在对称轴右边,y随x的增大而______(2)在对称轴左边y随x的增大而______。
练习4:已知二次函数y=ax2的图象如图,x1
0
x
y
1
2
3
4
1
2
-1
-2
x1
x2
知识梳理
考考你
(0,0)
Y轴
向上
最低
Y= x2
√
√
×
×
课本P30 A组 3、4题
P30 B组 1 题
同学们,
再见!
y=kx+b (k≠0)
y= (k≠0)
问:1.如何画出函数图象呢
2.如何得到相应的性质呢
直线
双曲线
列表
——
描点
——
连线
(描点法)
→
观察图象
总结性质
y=ax2 (a≠0)
图象:
性质:
k
x
二次函数
请同学们用描点法按下列要求画图:
请A组同学同桌合作画函数y=x2的图象;
请B组同学同桌合作画函数y= x2的图象。
0
y
3
4
1
2
x
1
2
-1
-2
0
y
3
4
1
2
x
1
2
-1
-2
…
2
0
2
…
…
4
1
0
1
4
…
y=x2
…
2
1
0
-1
-2
…
x
y= x2
1
2
9
8
1
8
3
2
9
4
9
8
9
4
1
8
1
4
1
4
1
2
1
2
1
2
3
2
1
2
y=x2
y= x2
1
2
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
用光滑曲线连结时要
自左向右顺次连结
0
y
3
4
1
2
x
1
2
-1
-2
0
y
3
4
1
2
x
1
2
-1
-2
y= x2
1
2
y=x2
形如物体抛射时所经过的路线的图象
0
y
3
4
1
2
x
1
2
-1
-2
0
y
3
4
1
2
x
1
2
-1
-2
y=x2
y= x2
1
2
对称轴
对称轴
顶点
顶点
向上
y轴
(0,0)
最低
减小
增大
请同学们用描点法按下列要求画图:
请A组的同学同桌合作在和抛物线y=x2同一坐标系中画函数y=-x2的图象,并观察;
请B组同学同桌合作在和抛物线y= x2同一坐标系中画函数y=- x2的图象,并观察。
1
2
1
2
向下
原点
y轴
向上
原点
y轴
开口方向
顶点
对称轴
函数
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y=-x2
y=x2
y= x2
1
2
y=- x2
1
2
向下
原点
y轴
向上
原点
y轴
开口方向
顶点
对称轴
函数
y=x2
y=-x2
y= x2
1
2
y=- x2
1
2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y=-x2
y=x2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y= x2
1
2
y=- x2
1
2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y=-x2
y=x2
y= x2
1
2
y=- x2
1
2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
0
x
y
1
2
3
4
1
2
-1
-2
-3
-4
-1
-2
y=-x2
y=x2
y= x2
1
2
y=- x2
1
2
y= x2
1
2
y=- x2
1
2
向下
y轴
(0,0)
最高
增大
减小
练习1:分别说出抛物线y=4x2与y=-5x2的开口方向,对称轴与顶点坐标。
巩固练习
练习2 :对于函数y=2x2,下列结论正确的是( ).
A.当x取任何实数时,y的值总是正的
B.x的值增大,y的值也随着增大
C.x的值增大,y的值随着减小
D.图像关于y轴对称
练习3 :如何根据函数的图象,
(1)根据图象,求当y=2时,对应的x的值(精确到0.1);
(2)利用图象,求的 值(精确到0.1)。
D
0
x
y
1
2
3
4
1
2
-1
-2
y=x2
-
练习5:观察上面画的图象回答:(1)在对称轴右边,y随x的增大而______(2)在对称轴左边y随x的增大而______。
练习4:已知二次函数y=ax2的图象如图,x1
0
x
y
1
2
3
4
1
2
-1
-2
x1
x2
知识梳理
考考你
(0,0)
Y轴
向上
最低
Y= x2
√
√
×
×
课本P30 A组 3、4题
P30 B组 1 题
同学们,
再见!
