2021-2022学年冀教版八年级数学上册第13章 全等三角形 同步测试卷 (Word版含答案)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册第13章 全等三角形 同步测试卷 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 263.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 14:53:12 | ||
图片预览

文档简介
第13章 全等三角形 同步测试卷 2021-2022学年冀教版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
下列命题的逆命题是真命题的是( )
A. 若,则 B. 同位角相等,两直线平行
C. 对顶角相等 D. 若,,则
如图,AB与CD相交于点E,AD=CB,要使ADECBE,需添加一个条件,则添加的条件以及相应的依据正确的是( )
A. B.
C. D.
如图,ABCA'B'C,若B=,A=,A'CB=,则B'CB的度数为( )
A. B. C. D.
如图,已知ABC=DCB,能直接用SAS证明ABCDCB的条件是( )
A. B.
C. D.
已知线段a,b和m,求作ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序是( )延长CD到B,使BD=CD;
连接AB;
作ADC,使DC=a,AC=b,AD=m.
A. B. C. D.
如图,点M在射线OB上,可以通过尺规作出BMN=BOA.从而可以“过点M作MNOA”.以上作图的依据中没有的是( )
A. 全等三角形的对应角相等 B. 三边对应相等的两个三角形全等
C. 两直线平行,同位角相等 D. 两点确定一条直线
如图,AB=AC,点D、E分别是AB、AC上一点,AD=AE,BE、CD相交于点M.若BAC=,C=,则BMD的大小为( )
A. B. C. D.
小明发现有两个结论:在与中,
若=,=,=,且它们的周长相等,则;
若=,=,=,则.对于上述的两个结论,下列说法正确的是( )
A. ,都错误 B. ,都正确
C. 正确,错误 D. 错误,正确
如图,ABC中,B=C=,BD=CE,BE=CF,则DEF的度数是( )
A. B. C. D.
二、填空题(本大题共6小题,共18分)
如图,在安装电线杆的横梁时通常斜着安装一个支架,这种做法的数学原理是 .
命题“全等三角形的对应角相等”的逆命题是 .
小涛在家打扫卫生,一不小心把一块三角形的玻璃台板打碎了,如图所示,如果要配一块完全一样的玻璃,至少要带的玻璃碎片序号是 .
如图,ABCDEC,ACB=,BCD=,点A在线段ED上,则B的度数为 度.
如图,四边形ABCD的对角线AC、BD相交于点O,ABOADO.下列结论:
ACBD;CB=CD;ABCADC; DA=DC.其中所有正确结论的序号是 .
如图,AB= 12 m,CAAB于A,DBAB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后CAP与PQB全等.
三、解答题(本大题共6小题,共72分)
已知,,线段a,如图所示.求作ABC,使BC=a,ABC与的补角相等,ACB=.
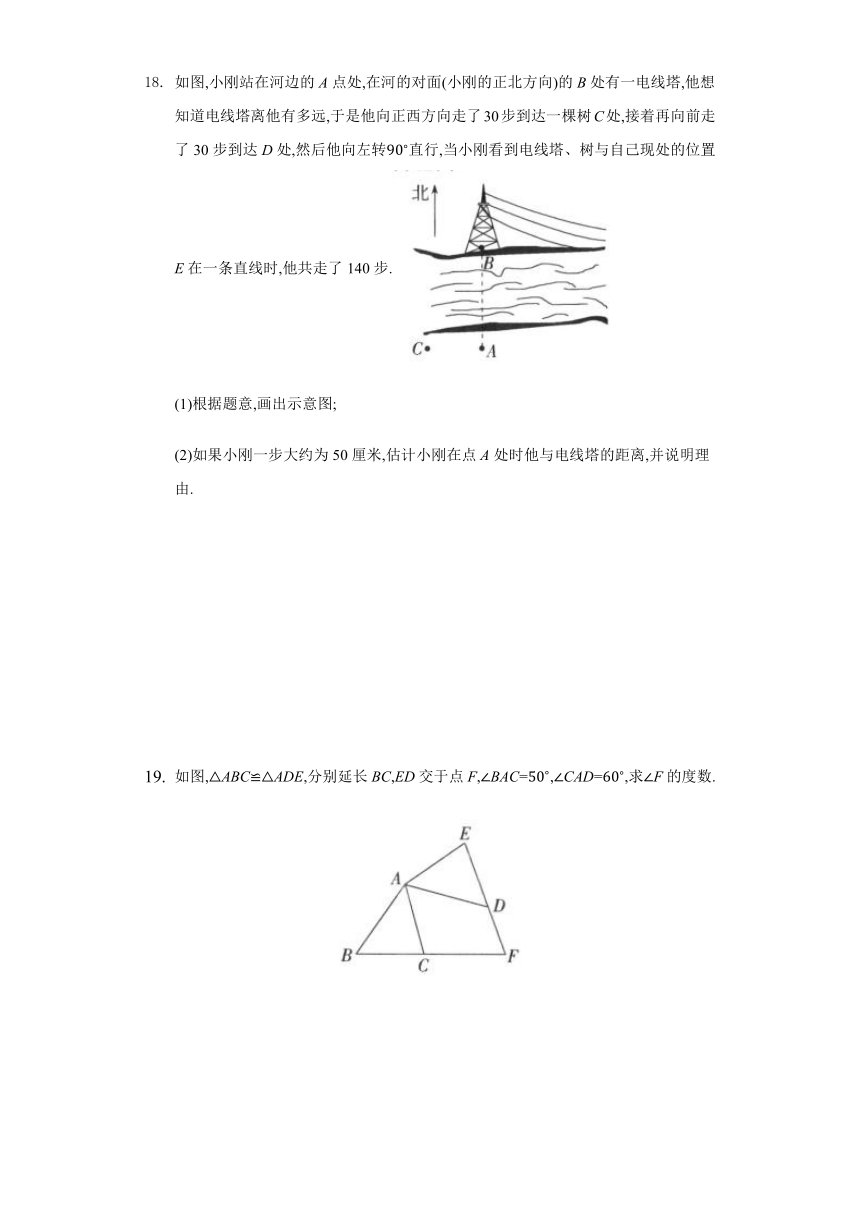
如图,小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他向左转直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约为50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.
如图,ABCADE,分别延长BC,ED交于点F,BAC=,CAD=,求F的度数.
如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)ABCD;
(2)ABCBAD.
如图,在ABC中,AB=AC,点E,F在边BC上,连接AE,AF,BAF=CAE,延长AF至点D,使AD=AC,连接CD.
(1)求证:ABEACF;
(2)若ACF=,AEB=,求ADC的度数.
22.如图,在ABC中,ACB是直角,B=,AD、CE分别是BAC、BCA的平分线, AD、CE相交于点F.
(1)请你判断并写出FE与FD之间的数量关系(不需证明);
(2)如图,如果ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立 若成立,请证明;若不成立,请说明理由.
1.【答案】D
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】三角形具有稳定性
12.【答案】三个角对应相等的两个三角形全等
13.【答案】(或或)
14.【答案】50
15.【答案】
16.【答案】 4
17.【答案】解:如图.作法:(1)作直线MN,并在MN上取点B;
(2)作MBP=;
(3)在BN上截取线段BC=a;
(4)作MCQ=,射线CQ,BP相交于点A.
ABC即为所求作的三角形.
18.【答案】解:(1)所画示意图如图:
(2)在DEC和ABC中,
DECABC(ASA),
AB=DE,
又小刚共走了140步,其中向正西方向走了60步,
DE=80步,
小刚一步大约为0.5米,
DE=800.5=40米.
答:小刚在点A处时他与电线塔的距离约为40米.
19.【答案】解:ABCADE,
EAD=BAC=,ACB=E,
B+E=B+ACB=-BAC=,
CAD=,
BAE=,
F=-B-E-BAE=.
20.【答案】解:证明(1)OA=OB,OC=OD,
OAB=OBA,OCD=ODC,
COD=AOB,OAB+OBA+AOB=,OCD+ODC+COD=,
OAB=OBA=OCD=ODC,
即OAB=OCD,
ABCD.
(2)OA=OB,OC=OD,
AC=BD,
在ABC和BAD中,
ABCBAD(SAS).
21.【答案】解:(1)证明:AB=AC,
B=ACF,
BAF=CAE,
BAF-EAF=CAE-EAF,
BAE=CAF,
在ABE和ACF中,
ABEACF(ASA).
(2)B=ACF=,AEB=,
BAE=--=,
CAF=BAE=,
AD=AC,
ADC=ACD,
ADC==.
22.【答案】解:(1)FE=FD.
(2)成立.证明:如图,在AC上取点G,使AG=AE,连接FG.
B=,AD、CE分别平分BAC、BCA,
1=2,3=4,1+2+3+4=.
2+3=.
在AEF和AGF中,
AEFAGF(SAS).
AFE=AFG,FE=FG.
AFE=CFD=AFG=.
CFG=.
在CFG和CFD中,
CFGCFD(ASA).
FG=FD.
FE=FD.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列各组中的两个图形属于全等图形的是( )
A. B.
C. D.
下列命题的逆命题是真命题的是( )
A. 若,则 B. 同位角相等,两直线平行
C. 对顶角相等 D. 若,,则
如图,AB与CD相交于点E,AD=CB,要使ADECBE,需添加一个条件,则添加的条件以及相应的依据正确的是( )
A. B.
C. D.
如图,ABCA'B'C,若B=,A=,A'CB=,则B'CB的度数为( )
A. B. C. D.
如图,已知ABC=DCB,能直接用SAS证明ABCDCB的条件是( )
A. B.
C. D.
已知线段a,b和m,求作ABC,使BC=a,AC=b,BC边上的中线AD=m,作法合理的顺序是( )延长CD到B,使BD=CD;
连接AB;
作ADC,使DC=a,AC=b,AD=m.
A. B. C. D.
如图,点M在射线OB上,可以通过尺规作出BMN=BOA.从而可以“过点M作MNOA”.以上作图的依据中没有的是( )
A. 全等三角形的对应角相等 B. 三边对应相等的两个三角形全等
C. 两直线平行,同位角相等 D. 两点确定一条直线
如图,AB=AC,点D、E分别是AB、AC上一点,AD=AE,BE、CD相交于点M.若BAC=,C=,则BMD的大小为( )
A. B. C. D.
小明发现有两个结论:在与中,
若=,=,=,且它们的周长相等,则;
若=,=,=,则.对于上述的两个结论,下列说法正确的是( )
A. ,都错误 B. ,都正确
C. 正确,错误 D. 错误,正确
如图,ABC中,B=C=,BD=CE,BE=CF,则DEF的度数是( )
A. B. C. D.
二、填空题(本大题共6小题,共18分)
如图,在安装电线杆的横梁时通常斜着安装一个支架,这种做法的数学原理是 .
命题“全等三角形的对应角相等”的逆命题是 .
小涛在家打扫卫生,一不小心把一块三角形的玻璃台板打碎了,如图所示,如果要配一块完全一样的玻璃,至少要带的玻璃碎片序号是 .
如图,ABCDEC,ACB=,BCD=,点A在线段ED上,则B的度数为 度.
如图,四边形ABCD的对角线AC、BD相交于点O,ABOADO.下列结论:
ACBD;CB=CD;ABCADC; DA=DC.其中所有正确结论的序号是 .
如图,AB= 12 m,CAAB于A,DBAB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动 分钟后CAP与PQB全等.
三、解答题(本大题共6小题,共72分)
已知,,线段a,如图所示.求作ABC,使BC=a,ABC与的补角相等,ACB=.
如图,小刚站在河边的A点处,在河的对面(小刚的正北方向)的B处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树C处,接着再向前走了30步到达D处,然后他向左转直行,当小刚看到电线塔、树与自己现处的位置E在一条直线时,他共走了140步.
(1)根据题意,画出示意图;
(2)如果小刚一步大约为50厘米,估计小刚在点A处时他与电线塔的距离,并说明理由.
如图,ABCADE,分别延长BC,ED交于点F,BAC=,CAD=,求F的度数.
如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)ABCD;
(2)ABCBAD.
如图,在ABC中,AB=AC,点E,F在边BC上,连接AE,AF,BAF=CAE,延长AF至点D,使AD=AC,连接CD.
(1)求证:ABEACF;
(2)若ACF=,AEB=,求ADC的度数.
22.如图,在ABC中,ACB是直角,B=,AD、CE分别是BAC、BCA的平分线, AD、CE相交于点F.
(1)请你判断并写出FE与FD之间的数量关系(不需证明);
(2)如图,如果ACB不是直角,其他条件不变,那么在(1)中所得的结论是否仍然成立 若成立,请证明;若不成立,请说明理由.
1.【答案】D
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】三角形具有稳定性
12.【答案】三个角对应相等的两个三角形全等
13.【答案】(或或)
14.【答案】50
15.【答案】
16.【答案】 4
17.【答案】解:如图.作法:(1)作直线MN,并在MN上取点B;
(2)作MBP=;
(3)在BN上截取线段BC=a;
(4)作MCQ=,射线CQ,BP相交于点A.
ABC即为所求作的三角形.
18.【答案】解:(1)所画示意图如图:
(2)在DEC和ABC中,
DECABC(ASA),
AB=DE,
又小刚共走了140步,其中向正西方向走了60步,
DE=80步,
小刚一步大约为0.5米,
DE=800.5=40米.
答:小刚在点A处时他与电线塔的距离约为40米.
19.【答案】解:ABCADE,
EAD=BAC=,ACB=E,
B+E=B+ACB=-BAC=,
CAD=,
BAE=,
F=-B-E-BAE=.
20.【答案】解:证明(1)OA=OB,OC=OD,
OAB=OBA,OCD=ODC,
COD=AOB,OAB+OBA+AOB=,OCD+ODC+COD=,
OAB=OBA=OCD=ODC,
即OAB=OCD,
ABCD.
(2)OA=OB,OC=OD,
AC=BD,
在ABC和BAD中,
ABCBAD(SAS).
21.【答案】解:(1)证明:AB=AC,
B=ACF,
BAF=CAE,
BAF-EAF=CAE-EAF,
BAE=CAF,
在ABE和ACF中,
ABEACF(ASA).
(2)B=ACF=,AEB=,
BAE=--=,
CAF=BAE=,
AD=AC,
ADC=ACD,
ADC==.
22.【答案】解:(1)FE=FD.
(2)成立.证明:如图,在AC上取点G,使AG=AE,连接FG.
B=,AD、CE分别平分BAC、BCA,
1=2,3=4,1+2+3+4=.
2+3=.
在AEF和AGF中,
AEFAGF(SAS).
AFE=AFG,FE=FG.
AFE=CFD=AFG=.
CFG=.
在CFG和CFD中,
CFGCFD(ASA).
FG=FD.
FE=FD.
第2页,共3页
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
