2021-2022学年苏科版七年级数学上册第六章 平面图形的认识(一) 同步测试卷(Word版含简答)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学上册第六章 平面图形的认识(一) 同步测试卷(Word版含简答) |  | |
| 格式 | docx | ||
| 文件大小 | 232.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 14:57:51 | ||
图片预览




文档简介
第六章平面图形的认识(一)同步测试卷 2021-2022学年苏科版七年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列现象中,可以用“两点之间线段最短”来解释的是( )
A. 把弯曲的公路改直,就能缩短路程
B. 打靶的时候,眼睛要与枪上的准星、靶心在同一条直线上
C. 利用圆规可以比较两条线段的大小
D. 用两个钉子就可以把木条固定在墙上
在一条直线上,依次有E、F、G、H四点.如果点F是线段EG的中点,点G是线段FH的中点,则有( )
A. B. C. D.
如图,下列说法正确的是( )
A. 的方向是北偏东
B. 的方向是南偏东
C. 的方向是南偏西
D. 的方向是北偏西
若A=18',B=15'30″,C=60.,则( )
A. B.
C. D.
已知=,则的余角是( )
A. B. C. D.
如图,下列说法中正确的是( )
A. 直线在线段上
B. 射线与直线没有公共点
C. 直线与线段相交于点
D. 点在直线上
如图,已知AB、CD相交于点O,OEAB,EOC =,则AOD=( )
A. B.
C. D.
如图,已知1=15',则2的度数为( )
A. B. C. D.
现在的时间是上午9点20分,此时钟面上的时针与分针的夹角是( )
A. B. C. D.
同一平面内的四条直线,最多有m个交点,最少有n个交点,那么是( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
小明想度量图中点C到三角形ABC的边AB所在直线的距离,在老师的指导下小明完成了画图,那么 就是点C到直线AB的距离.
在直线l的同侧有A、B、C三点,如果A、B两点确定的直线与B、C两点确定的直线都与直线平行,则A、B、C三点的位置关系是 ,理论依据是 .
下列说法:两条不相交的直线叫平行线;两条不相交的线段,在同一平面内必平行;经过直线外一点有且只有一条直线与这条直线平行;若直线ab,ac,则bc.其中错误的有 个.
将一副三角尺的直角顶点重合并按如图所示的方式摆放,当AD平分BAC时,CAE= .
画线段AB=1cm,延长线段AB到C,使线段BC= 2 cm,已知点D是线段BC的中点,则线段AD= cm.
以AOB的顶点O为端点引射线OP,使AOP:BOP=3:2,若AOB=,则AOP的度数为 .
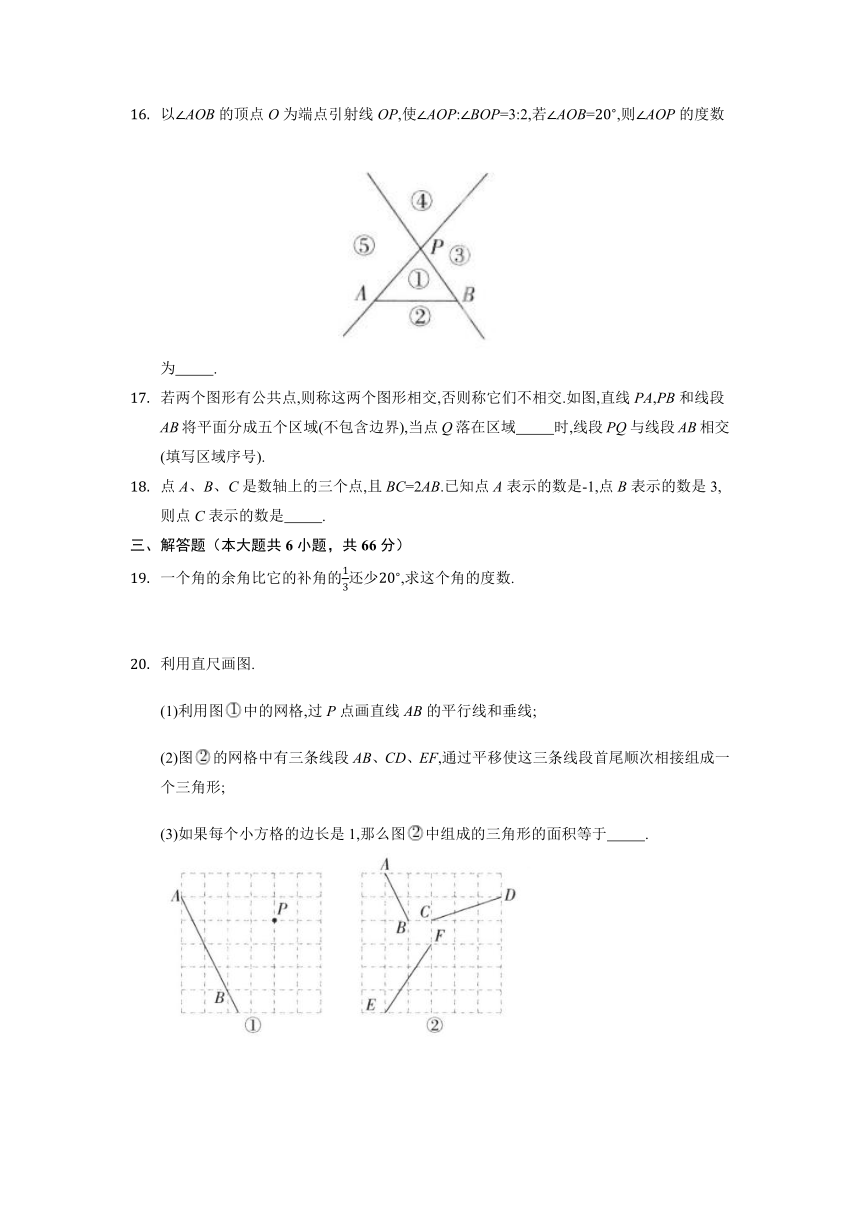
若两个图形有公共点,则称这两个图形相交,否则称它们不相交.如图,直线PA,PB和线段AB将平面分成五个区域(不包含边界),当点Q落在区域 时,线段PQ与线段AB相交(填写区域序号).
点A、B、C是数轴上的三个点,且BC=2AB.已知点A表示的数是-1,点B表示的数是3,则点C表示的数是 .
三、解答题(本大题共6小题,共66分)
一个角的余角比它的补角的还少,求这个角的度数.
利用直尺画图.
(1)利用图中的网格,过P点画直线AB的平行线和垂线;
(2)图的网格中有三条线段AB、CD、EF,通过平移使这三条线段首尾顺次相接组成一个三角形;
(3)如果每个小方格的边长是1,那么图中组成的三角形的面积等于 .
如图,BC=3AB,M、N是BC上的两点,且BM:MN=2:3,
MN:NC=2:5,AC=100cm,求AB、BM、MN、NC的长.
如图,直线AB、CD相交于点O,OE平分BOD.
(1)若AOC=,求BOE的度数;
(2)若OF平分AOD,试说明OEOF.
定义:从一个角的顶点出发,把这个角分成1:2的两个角的射线,叫做这个角的三分线,显然,一个角的三分线有两条.
(1)如图,OC是AOB的一条三分线,且BOC>AOC,若AOB=,求AOC的度数;
(2)如图,AOB=,若OC,OD是AOB的两条三分线.
求COD的度数;
现以O为中心,将COD顺时针旋转n度得到C'OD',当OA恰好是C'OD'的三分线时,求n的值.
如图,已知数轴上有A,B,C三点,分别表示数-24,-10,10.两只电子蚂蚁甲、乙分别从A, C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
(1)问甲、乙在数轴上的哪个点相遇
(2)问多少秒后,甲到A,B,C三点的距离之和为40个单位
(3)若甲、乙两只电子蚂蚁(用P表示甲蚂蚁、Q表示乙蚂蚁)分别从A,C两点同时相向而行,甲的速度变为原来的3倍,乙的速度不变,多少秒后,原点O、甲蚂蚁P与乙蚂蚁Q三点中,有一点恰好是另两点所连线段的中点
1.【答案】A
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】A
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】B
10.【答案】B
11.【答案】线段CD的长度
12.【答案】 在同一条直线上
过直线外一点有且只有一条直线与这条直线平行
13.【答案】2
14.【答案】
15.【答案】2
16.【答案】或
17.【答案】
18.【答案】11或-5
19.【答案】解:设这个角的度数为,则它的余角为,补角为(180- x).
根据题意,得=-,
解这个方程,得x =75.
故这个角的度数是.
20.【答案】解:(1)如图所示,MNAB,PQAB于点Q.
(2)如图所示,将CD平移到GF(或EH)的位置,将AB平移到GE(或FH)的位置.
(3)S三角形EFH=S三角形EFG=33-12-23-13=9-1-3-=3.5.
故答案为3.5.
21.【答案】解:因为BM:MN=2:3,MN:NC=2:5,
所以BM:MN:NC=4:6:15.
设BM=4x cm,x>0,则MN=6x cm,NC=15x cm.
所以BC=BM+MN+NC=4x+6x+15x=25x(cm).
因为BC=3AB,
所以AB=BC=x cm.
因为AC=100cm,AC=AB+BC,
所以x+25x=100,解得x=3.
故AB=3=25(cm),
BM=43=12(cm),
MN=63=18(cm),
NC=153=45(cm).
22.【答案】解: (1)因为直线AB、CD相交于点O,AOC=,
所以BOD=AOC=.
又因为OE平分BOD,
所以BOE=BOD=.
(2)因为OF平分AOD,
所以DOF=AOD.
又因为OE平分BOD,
所以DOE=BOD,
所以EOF=DOF+DOE=(AOD+BOD)==,
所以OEOF.
23.【答案】解:(1)OC是AOB的一条三分线,且BOC>AOC,
AOC=AOB.
又AOB=,
AOC=.
(2)如图,AOB=,OC,OD是AOB的两条三分线,
COD=AOB=.
分两种情况:
如图,当OA是C'OD'的三分线,且AOD'>AOC'时, AOC'=,
DOC'=-=,
DOD'=+=;
如图,当OA是C'OD'的三分线,且AOD'DOC'=-=,
DOD'=+=.
综上所述,n=40或50.
24.【答案】解:(1)设z秒后甲与乙相遇,则4z+6z=34,
解得z=3.4,
43.4=13.6,-24+13.6=-10.4.
故甲、乙在数轴上表示-10.4的点处相遇.
(2)设y秒后甲到A,B,C三点的距离之和为40个单位, B点距A,C两点的距离的和为14+20=34<40,A点距B,C两点的距离的和为14+34=48>40,C点距A,B两点的距离的和为34+20=54 >40,故甲应位于AB或BC之间.
当甲位于AB之间时,4y+(14-4y)+(14-4y+20)=40,解得y=2;
当甲位于BC之间时,4y+(4y-14)+(34-4y)=40,解得y=5.
故2秒或5秒后,甲到A,B,C三点的距离之和为40个单位.
(3)设x秒后原点O是甲蚂蚁P与乙蚂蚁Q两点所连线段的中点,则24-12x=10-6x,解得x=;
设x'秒后乙蚂蚁Q是甲蚂蚁P与原点O两点所连线段的中点,则24-12x'=2(6x'-10),解得x'=;
设x''秒后甲蚂蚁P是乙蚂蚁Q与原点O两点所连线段的中点,则2(24-12x'')=6x''-10,解得x''=.
综上所述,秒或秒或秒后,原点O、甲蚂蚁P与乙蚂蚁Q三点中,有一点恰好是另两点所连线段的中点.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
下列现象中,可以用“两点之间线段最短”来解释的是( )
A. 把弯曲的公路改直,就能缩短路程
B. 打靶的时候,眼睛要与枪上的准星、靶心在同一条直线上
C. 利用圆规可以比较两条线段的大小
D. 用两个钉子就可以把木条固定在墙上
在一条直线上,依次有E、F、G、H四点.如果点F是线段EG的中点,点G是线段FH的中点,则有( )
A. B. C. D.
如图,下列说法正确的是( )
A. 的方向是北偏东
B. 的方向是南偏东
C. 的方向是南偏西
D. 的方向是北偏西
若A=18',B=15'30″,C=60.,则( )
A. B.
C. D.
已知=,则的余角是( )
A. B. C. D.
如图,下列说法中正确的是( )
A. 直线在线段上
B. 射线与直线没有公共点
C. 直线与线段相交于点
D. 点在直线上
如图,已知AB、CD相交于点O,OEAB,EOC =,则AOD=( )
A. B.
C. D.
如图,已知1=15',则2的度数为( )
A. B. C. D.
现在的时间是上午9点20分,此时钟面上的时针与分针的夹角是( )
A. B. C. D.
同一平面内的四条直线,最多有m个交点,最少有n个交点,那么是( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
小明想度量图中点C到三角形ABC的边AB所在直线的距离,在老师的指导下小明完成了画图,那么 就是点C到直线AB的距离.
在直线l的同侧有A、B、C三点,如果A、B两点确定的直线与B、C两点确定的直线都与直线平行,则A、B、C三点的位置关系是 ,理论依据是 .
下列说法:两条不相交的直线叫平行线;两条不相交的线段,在同一平面内必平行;经过直线外一点有且只有一条直线与这条直线平行;若直线ab,ac,则bc.其中错误的有 个.
将一副三角尺的直角顶点重合并按如图所示的方式摆放,当AD平分BAC时,CAE= .
画线段AB=1cm,延长线段AB到C,使线段BC= 2 cm,已知点D是线段BC的中点,则线段AD= cm.
以AOB的顶点O为端点引射线OP,使AOP:BOP=3:2,若AOB=,则AOP的度数为 .
若两个图形有公共点,则称这两个图形相交,否则称它们不相交.如图,直线PA,PB和线段AB将平面分成五个区域(不包含边界),当点Q落在区域 时,线段PQ与线段AB相交(填写区域序号).
点A、B、C是数轴上的三个点,且BC=2AB.已知点A表示的数是-1,点B表示的数是3,则点C表示的数是 .
三、解答题(本大题共6小题,共66分)
一个角的余角比它的补角的还少,求这个角的度数.
利用直尺画图.
(1)利用图中的网格,过P点画直线AB的平行线和垂线;
(2)图的网格中有三条线段AB、CD、EF,通过平移使这三条线段首尾顺次相接组成一个三角形;
(3)如果每个小方格的边长是1,那么图中组成的三角形的面积等于 .
如图,BC=3AB,M、N是BC上的两点,且BM:MN=2:3,
MN:NC=2:5,AC=100cm,求AB、BM、MN、NC的长.
如图,直线AB、CD相交于点O,OE平分BOD.
(1)若AOC=,求BOE的度数;
(2)若OF平分AOD,试说明OEOF.
定义:从一个角的顶点出发,把这个角分成1:2的两个角的射线,叫做这个角的三分线,显然,一个角的三分线有两条.
(1)如图,OC是AOB的一条三分线,且BOC>AOC,若AOB=,求AOC的度数;
(2)如图,AOB=,若OC,OD是AOB的两条三分线.
求COD的度数;
现以O为中心,将COD顺时针旋转n度得到C'OD',当OA恰好是C'OD'的三分线时,求n的值.
如图,已知数轴上有A,B,C三点,分别表示数-24,-10,10.两只电子蚂蚁甲、乙分别从A, C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
(1)问甲、乙在数轴上的哪个点相遇
(2)问多少秒后,甲到A,B,C三点的距离之和为40个单位
(3)若甲、乙两只电子蚂蚁(用P表示甲蚂蚁、Q表示乙蚂蚁)分别从A,C两点同时相向而行,甲的速度变为原来的3倍,乙的速度不变,多少秒后,原点O、甲蚂蚁P与乙蚂蚁Q三点中,有一点恰好是另两点所连线段的中点
1.【答案】A
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】A
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】B
10.【答案】B
11.【答案】线段CD的长度
12.【答案】 在同一条直线上
过直线外一点有且只有一条直线与这条直线平行
13.【答案】2
14.【答案】
15.【答案】2
16.【答案】或
17.【答案】
18.【答案】11或-5
19.【答案】解:设这个角的度数为,则它的余角为,补角为(180- x).
根据题意,得=-,
解这个方程,得x =75.
故这个角的度数是.
20.【答案】解:(1)如图所示,MNAB,PQAB于点Q.
(2)如图所示,将CD平移到GF(或EH)的位置,将AB平移到GE(或FH)的位置.
(3)S三角形EFH=S三角形EFG=33-12-23-13=9-1-3-=3.5.
故答案为3.5.
21.【答案】解:因为BM:MN=2:3,MN:NC=2:5,
所以BM:MN:NC=4:6:15.
设BM=4x cm,x>0,则MN=6x cm,NC=15x cm.
所以BC=BM+MN+NC=4x+6x+15x=25x(cm).
因为BC=3AB,
所以AB=BC=x cm.
因为AC=100cm,AC=AB+BC,
所以x+25x=100,解得x=3.
故AB=3=25(cm),
BM=43=12(cm),
MN=63=18(cm),
NC=153=45(cm).
22.【答案】解: (1)因为直线AB、CD相交于点O,AOC=,
所以BOD=AOC=.
又因为OE平分BOD,
所以BOE=BOD=.
(2)因为OF平分AOD,
所以DOF=AOD.
又因为OE平分BOD,
所以DOE=BOD,
所以EOF=DOF+DOE=(AOD+BOD)==,
所以OEOF.
23.【答案】解:(1)OC是AOB的一条三分线,且BOC>AOC,
AOC=AOB.
又AOB=,
AOC=.
(2)如图,AOB=,OC,OD是AOB的两条三分线,
COD=AOB=.
分两种情况:
如图,当OA是C'OD'的三分线,且AOD'>AOC'时, AOC'=,
DOC'=-=,
DOD'=+=;
如图,当OA是C'OD'的三分线,且AOD'
DOD'=+=.
综上所述,n=40或50.
24.【答案】解:(1)设z秒后甲与乙相遇,则4z+6z=34,
解得z=3.4,
43.4=13.6,-24+13.6=-10.4.
故甲、乙在数轴上表示-10.4的点处相遇.
(2)设y秒后甲到A,B,C三点的距离之和为40个单位, B点距A,C两点的距离的和为14+20=34<40,A点距B,C两点的距离的和为14+34=48>40,C点距A,B两点的距离的和为34+20=54 >40,故甲应位于AB或BC之间.
当甲位于AB之间时,4y+(14-4y)+(14-4y+20)=40,解得y=2;
当甲位于BC之间时,4y+(4y-14)+(34-4y)=40,解得y=5.
故2秒或5秒后,甲到A,B,C三点的距离之和为40个单位.
(3)设x秒后原点O是甲蚂蚁P与乙蚂蚁Q两点所连线段的中点,则24-12x=10-6x,解得x=;
设x'秒后乙蚂蚁Q是甲蚂蚁P与原点O两点所连线段的中点,则24-12x'=2(6x'-10),解得x'=;
设x''秒后甲蚂蚁P是乙蚂蚁Q与原点O两点所连线段的中点,则2(24-12x'')=6x''-10,解得x''=.
综上所述,秒或秒或秒后,原点O、甲蚂蚁P与乙蚂蚁Q三点中,有一点恰好是另两点所连线段的中点.
第2页,共2页
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
