26.2.1 现实生活中的反比例函数问题同步练习(含答案)
文档属性
| 名称 | 26.2.1 现实生活中的反比例函数问题同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-30 16:46:00 | ||
图片预览




文档简介
26.2 实际问题与反比例函数
第1课时 现实生活中的反比例函数问题
一、选择题
1.若三角形框的面积一定,则这个三角形框的底边长a和底边上的高b之间的函数图象大致为( )
2.为了抵御洪水,长江无为大堤展开加固工程,该工程建设需要运送大量土石方.某运输公司承担了运送总量为108 m3土石方的任务,该运输公司平均运送土石方的速度v(m3/天)与完成运送任务所需时间t(天)之间的函数关系式是( )
A.v= B.v=108t C.v=t2 D.v=108t2
3.今年,华为公司推出的一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9 688元的新手机,前期付款2 000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是 ( )
A.y=+2 000 B.y=-2000 C.y= D.y=
4.用规格为50 cm×50 cm的地板砖密铺客厅恰好需要60块.如果改用规格为a cm×a cm的地板砖y块也恰好能密铺该客厅,那么y与a之间的关系式为( )
A.y= B.y= C.y=150 000a2 D.y=150 000a
5.【2021·宜昌】某气球内充满了一定质量m的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=,能够反映两个变量p和V函数关系的图象是( )
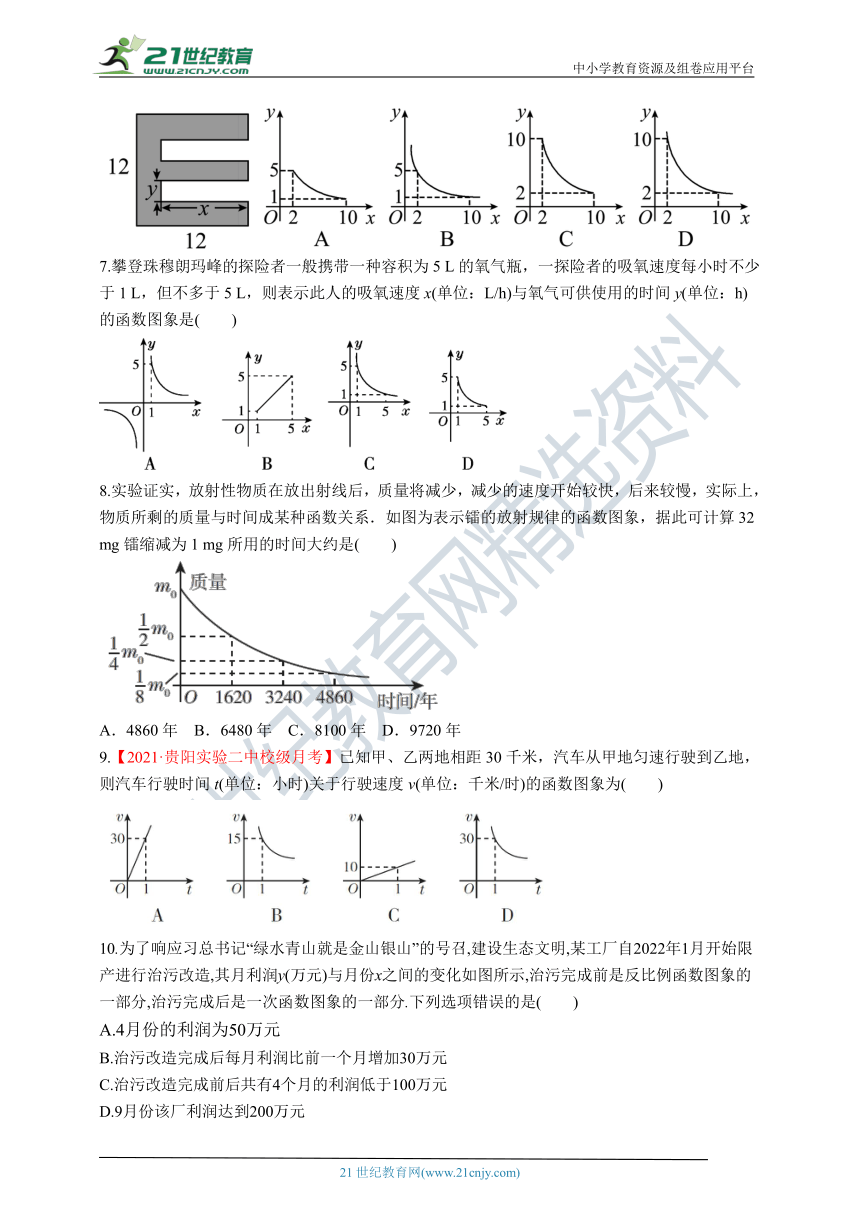
6.如图,一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
7.攀登珠穆朗玛峰的探险者一般携带一种容积为5 L的氧气瓶,一探险者的吸氧速度每小时不少于1 L,但不多于5 L,则表示此人的吸氧速度x(单位:L/h)与氧气可供使用的时间y(单位:h)的函数图象是( )
8.实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.如图为表示镭的放射规律的函数图象,据此可计算32 mg镭缩减为1 mg所用的时间大约是( )
A.4860年 B.6480年 C.8100年 D.9720年
9.【2021·贵阳实验二中校级月考】已知甲、乙两地相距30千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/时)的函数图象为( )
10.为了响应习总书记“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2022年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分.下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
第10题图 第11题图 第12题图
11.【2021·太原期末改编】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=(k≠0)的一部分,则当x=16时,大棚内的温度为( )
A.18 ℃ B.15.5 ℃ C.13.5 ℃ D.12 ℃
12.如图①,在矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图②所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )
A.当x=3时,EC<EM B.当x=9时,EC<EM
C.当x增大时,BE·DF的值不变 D.当x增大时,EC·CF的值增大
二、填空题
13.如图是一个蓄水池每小时的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数关系图象,若要5 h排完水池中的水,则每小时的排水量应为____m3/h.
第13题图 第15题图 第17题图 第18题图
14.把一个长、宽、高分别为3 cm,2 cm,1 cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为 .
15.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式t=,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).若行驶速度不得超过60 km/h,则汽车通过该路段最少需要时间为 h.
16.某商品售价y(元/件)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比例,根据表格写出y与x的函数关系式为 .
售价y/(元·件-1) 11 10
月需求量x/件 100 120
17.随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速低于20千米/时时,交通就会拥堵.为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是 .
18.秋季是传染病的高发季节.为预防传染病,某学校会定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10 min燃烧完,此时教室内每立方米空气中的含药量为6 mg.研究表明当每立方米空气中的含药量不低于1.2 mg时,消毒才有效,则这次有效的消毒时间是 min.
三、解答题
19.某养鱼专业户准备挖一个面积为2000米2的长方形鱼塘.
(1)求鱼塘的长y(米)关于宽x(米)的函数解析式.
(2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米时,鱼塘的长为多少米
20.某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(吨)与运输时间x(天)之间有怎样的函数关系式
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务.求原计划完成运输任务的天数.
21.一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)求v与t的函数关系式及t的取值范围;
(2)客车上午8时从甲地出发.
①客车需在当天14时40分至15时30分(含14时40分与15时30分)间到达乙地,求客车行驶速度v的范围;
②客车能否在当天12时30分前到达乙地 说明理由.
22.某汽车销售商推出分期付款购车促销活动,交付首付款后,余额要在30个月内结清,不计算利息.王先生在活动期间购买了一辆价格为12万元的汽车,交了首付款后平均每月付款y万元,x个月结清,y与x成反比例,其函数图象如图所示.根据图象回答下列问题:
(1)求y关于x的函数解析式,并求出首付款的钱数.
(2)若王先生用20个月结清,则平均每月应付多少万元
(3)如果打算每月付款不超过4 000元,那么王先生至少要用多少个月才能结清余款
23.小明要把一篇文章录入电脑,已知他完成录入的时间y(分钟)与录入文字的速度x(字/分钟)之间的函数关系如图所示.
(1)求y与x之间的函数解析式.
(2)若小明在19:20开始录入,完成录入时间不超过19:35,小明每分钟至少应录入多少字
(3)小明为了收看19:30的《新闻联播》,将原定的录入速度提高了20%,结果比原计划提前2分钟完成,小明实际用了多少分钟完成文章的录入
24.【2021·乐山】通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平衡状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值.
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标不低于36?请说明理由.
25【河北中考】长为300 m的春游队伍,以v(m/s)的速度向东行进,如图①和图②,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围);
(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.若三角形框的面积一定,则这个三角形框的底边长a和底边上的高b之间的函数图象大致为( C )
2.为了抵御洪水,长江无为大堤展开加固工程,该工程建设需要运送大量土石方.某运输公司承担了运送总量为108 m3土石方的任务,该运输公司平均运送土石方的速度v(m3/天)与完成运送任务所需时间t(天)之间的函数关系式是( A )
A.v= B.v=108t C.v=t2 D.v=108t2
3.今年,华为公司推出的一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9 688元的新手机,前期付款2 000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是 ( C )
A.y=+2 000 B.y=-2000 C.y= D.y=
4.用规格为50 cm×50 cm的地板砖密铺客厅恰好需要60块.如果改用规格为a cm×a cm的地板砖y块也恰好能密铺该客厅,那么y与a之间的关系式为( A )
A.y= B.y= C.y=150 000a2 D.y=150 000a
5.【2021·宜昌】某气球内充满了一定质量m的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=,能够反映两个变量p和V函数关系的图象是( B )
6.如图,一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( A )
7.攀登珠穆朗玛峰的探险者一般携带一种容积为5 L的氧气瓶,一探险者的吸氧速度每小时不少于1 L,但不多于5 L,则表示此人的吸氧速度x(单位:L/h)与氧气可供使用的时间y(单位:h)的函数图象是( D )
【点拨】氧气瓶容积一定,则吸氧速度x与氧气可供使用的时间y成反比例函数关系.由题意知y=,又1≤x≤5,所以1≤y≤5.故选D.
【答案】D
8.实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.如图为表示镭的放射规律的函数图象,据此可计算32 mg镭缩减为1 mg所用的时间大约是( C )
A.4860年 B.6480年 C.8100年 D.9720年
【点拨】由题图可知:1620年时,镭质量缩减为原来的,再经过1620年,即当3240年时,镭质量缩减为原来的=,再经过1620×2=3240年,即当4860年时,镭质量缩减为原来的=,
∴再经过1620×4=6480年,
即当8100年时,镭质量缩减为原来的=,
此时32×=1(mg),
故选C.
9.【2021·贵阳实验二中校级月考】已知甲、乙两地相距30千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/时)的函数图象为( D )
10.为了响应习总书记“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2022年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分.下列选项错误的是( C )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
第10题图 第11题图 第12题图
11.【2021·太原期末改编】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=(k≠0)的一部分,则当x=16时,大棚内的温度为( C )
A.18 ℃ B.15.5 ℃ C.13.5 ℃ D.12 ℃
12.如图①,在矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图②所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( C )
A.当x=3时,EC<EM B.当x=9时,EC<EM
C.当x增大时,BE·DF的值不变 D.当x增大时,EC·CF的值增大
【点拨】易知△BEC和△DCF都是等腰直角三角形.观察反比例函数图象可知当x=3时,y=3,则反比例函数的解析式为y=.
A选项,当x=3时,y=3,即BC=CD=3,所以CE=BC=3,CF=CD=3,所以C点与M点重合,则EC=EM,故A错误.
B选项,当x=9时,y=1,即BC=9,CD=1,所以EC=9,EF=10.所以EM=5.所以EC>EM,故B错误.
C选项,BE·DF=BC·CD=xy=9,即BE·DF的值不变,故C正确.
D选项,因为EC·CF=x·y=2·xy=18,故EC·CF为定值,故D错误.
二、填空题
13.如图是一个蓄水池每小时的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数关系图象,若要5 h排完水池中的水,则每小时的排水量应为____m3/h.
【答案】9.6
第13题图 第15题图 第17题图 第18题图
14.把一个长、宽、高分别为3 cm,2 cm,1 cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为 S= .
15.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式t=,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).若行驶速度不得超过60 km/h,则汽车通过该路段最少需要时间为 h.
16.某商品售价y(元/件)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比例,根据表格写出y与x的函数关系式为 y=+5 .
售价y/(元·件-1) 11 10
月需求量x/件 100 120
17.随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速低于20千米/时时,交通就会拥堵.为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是 .
【答案】018.秋季是传染病的高发季节.为预防传染病,某学校会定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10 min燃烧完,此时教室内每立方米空气中的含药量为6 mg.研究表明当每立方米空气中的含药量不低于1.2 mg时,消毒才有效,则这次有效的消毒时间是 min.
【答案】48
三、解答题
19.某养鱼专业户准备挖一个面积为2000米2的长方形鱼塘.
(1)求鱼塘的长y(米)关于宽x(米)的函数解析式.
(2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米时,鱼塘的长为多少米
解:(1)由长方形面积为2000米2,得到xy=2000,即y=.
(2)当x=20时,y==100,
答:当鱼塘的宽是20米时,鱼塘的长为100米.
20.某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(吨)与运输时间x(天)之间有怎样的函数关系式
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务.求原计划完成运输任务的天数.
解:(1)由题意,得xy=3000,∴y=(x>0).
(2)设原计划x天完成运输任务.
根据题意,得,解得x=4.
经检验x=4是原分式方程的根,且符合题意.
答:原计划4天完成运输任务.
21.一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)求v与t的函数关系式及t的取值范围;
(2)客车上午8时从甲地出发.
①客车需在当天14时40分至15时30分(含14时40分与15时30分)间到达乙地,求客车行驶速度v的范围;
②客车能否在当天12时30分前到达乙地 说明理由.
解:(1)设v与t的函数关系式为v=(k≠0),
将(5,120)代入v=,
解得k=600,
∴v与t的函数关系式为v=(5≤t≤10).
(2)①当t=时,v=80,
∴客车行驶速度v的范围为80≤v≤90.
②不能.
理由:若客车在当天12时30分到达,则t=4.5<5,
而5≤t≤10,故客车不能在当天12时30分前到达乙地.
22.某汽车销售商推出分期付款购车促销活动,交付首付款后,余额要在30个月内结清,不计算利息.王先生在活动期间购买了一辆价格为12万元的汽车,交了首付款后平均每月付款y万元,x个月结清,y与x成反比例,其函数图象如图所示.根据图象回答下列问题:
(1)求y关于x的函数解析式,并求出首付款的钱数.
(2)若王先生用20个月结清,则平均每月应付多少万元
(3)如果打算每月付款不超过4 000元,那么王先生至少要用多少个月才能结清余款
解:(1)设y关于x的函数解析式为y=(k≠0),
把(5,1.8)代入y=(k≠0),得k=9,
∴y=(0<x≤30,且x为正整数).
∴余额为9万元,12-9=3(万元),
∴首付款为3万元.
(2)当x=20时,y==0.45.
∴平均每月应付0.45万元.
(3)由题意,知≤0.4,∴x≥22.5.
∵x为正整数,∴王先生至少要用23个月才能结清余款.
23.小明要把一篇文章录入电脑,已知他完成录入的时间y(分钟)与录入文字的速度x(字/分钟)之间的函数关系如图所示.
(1)求y与x之间的函数解析式.
(2)若小明在19:20开始录入,完成录入时间不超过19:35,小明每分钟至少应录入多少字
(3)小明为了收看19:30的《新闻联播》,将原定的录入速度提高了20%,结果比原计划提前2分钟完成,小明实际用了多少分钟完成文章的录入
解:(1)设y关于x的函数解析式为y=(k≠0).
把点(150,10)代入,得10=,∴k=1500,
∴y与x之间的函数解析式为y=.
(2)∵k>0,在第一象限内,y随x的增大而减小,
∴当y≤15时,x≥100.
答:小明每分钟至少录入100字.
(3)设小明实际用了t分钟,则原计划用时(t+2)分钟.
由题意,得(1+20%)×,解得t=10,
经检验t=10是原分式方程的解,且符合题意.
答:小明实际用了10分钟完成文章的录入.
24.【2021·乐山】通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平衡状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值.
解:设当20≤x≤45时,反比例函数的解析式为y=.
将C(20,45)的坐标代入,得45=,解得k=900.
∴反比例函数的解析式为y=.
当x=45时,y==20,∴D(45,20).
∴A(0,20),即A对应的指标值为20.
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标不低于36?请说明理由.
解:设当0≤x<10时,线段AB的解析式为y=mx+n.
将A(0,20),B(10,45)的坐标代入,
得解得
∴线段AB的解析式为y=x+20(0≤x<10).
当y≥36时,x+20≥36,解得x≥.
由(1)得反比例函数的解析式为y=.
当y≥36时,≥36,解得x≤25,
∴当≤x≤25时,注意力指标不低于36.
∵25-=>17,∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标不低于36.
25【河北中考】长为300 m的春游队伍,以v(m/s)的速度向东行进,如图①和图②,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围);
(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
解:(1)①排尾从位置O开始行进的时间为t(s),则排头也离开原排头t(s),
∴S头=2t+300 ②甲从排尾赶到排头的时间为300÷(2v-v)=300÷v=300÷2=150(s),此时S头=2t+300=600(m),甲返回时间为:(t-150)s,
∴S甲=S头-S甲回=2×150+300-4(t-150)=-4t+1200;
因此,S头与t的函数关系式为S头=2t+300,当甲赶到排头位置时,S头的值为600 m;
在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=-4t+1200
(2)T=t追及+t返回=+=,在甲这次往返队伍的过程中队伍行进的路程为:v×=400;因此T与v的函数关系式为:T=,此时队伍在此过程中行进的路程为400 m
第1课时 现实生活中的反比例函数问题
一、选择题
1.若三角形框的面积一定,则这个三角形框的底边长a和底边上的高b之间的函数图象大致为( )
2.为了抵御洪水,长江无为大堤展开加固工程,该工程建设需要运送大量土石方.某运输公司承担了运送总量为108 m3土石方的任务,该运输公司平均运送土石方的速度v(m3/天)与完成运送任务所需时间t(天)之间的函数关系式是( )
A.v= B.v=108t C.v=t2 D.v=108t2
3.今年,华为公司推出的一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9 688元的新手机,前期付款2 000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是 ( )
A.y=+2 000 B.y=-2000 C.y= D.y=
4.用规格为50 cm×50 cm的地板砖密铺客厅恰好需要60块.如果改用规格为a cm×a cm的地板砖y块也恰好能密铺该客厅,那么y与a之间的关系式为( )
A.y= B.y= C.y=150 000a2 D.y=150 000a
5.【2021·宜昌】某气球内充满了一定质量m的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=,能够反映两个变量p和V函数关系的图象是( )
6.如图,一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( )
7.攀登珠穆朗玛峰的探险者一般携带一种容积为5 L的氧气瓶,一探险者的吸氧速度每小时不少于1 L,但不多于5 L,则表示此人的吸氧速度x(单位:L/h)与氧气可供使用的时间y(单位:h)的函数图象是( )
8.实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.如图为表示镭的放射规律的函数图象,据此可计算32 mg镭缩减为1 mg所用的时间大约是( )
A.4860年 B.6480年 C.8100年 D.9720年
9.【2021·贵阳实验二中校级月考】已知甲、乙两地相距30千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/时)的函数图象为( )
10.为了响应习总书记“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2022年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分.下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
第10题图 第11题图 第12题图
11.【2021·太原期末改编】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=(k≠0)的一部分,则当x=16时,大棚内的温度为( )
A.18 ℃ B.15.5 ℃ C.13.5 ℃ D.12 ℃
12.如图①,在矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图②所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( )
A.当x=3时,EC<EM B.当x=9时,EC<EM
C.当x增大时,BE·DF的值不变 D.当x增大时,EC·CF的值增大
二、填空题
13.如图是一个蓄水池每小时的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数关系图象,若要5 h排完水池中的水,则每小时的排水量应为____m3/h.
第13题图 第15题图 第17题图 第18题图
14.把一个长、宽、高分别为3 cm,2 cm,1 cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为 .
15.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式t=,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).若行驶速度不得超过60 km/h,则汽车通过该路段最少需要时间为 h.
16.某商品售价y(元/件)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比例,根据表格写出y与x的函数关系式为 .
售价y/(元·件-1) 11 10
月需求量x/件 100 120
17.随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速低于20千米/时时,交通就会拥堵.为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是 .
18.秋季是传染病的高发季节.为预防传染病,某学校会定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与燃烧时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10 min燃烧完,此时教室内每立方米空气中的含药量为6 mg.研究表明当每立方米空气中的含药量不低于1.2 mg时,消毒才有效,则这次有效的消毒时间是 min.
三、解答题
19.某养鱼专业户准备挖一个面积为2000米2的长方形鱼塘.
(1)求鱼塘的长y(米)关于宽x(米)的函数解析式.
(2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米时,鱼塘的长为多少米
20.某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(吨)与运输时间x(天)之间有怎样的函数关系式
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务.求原计划完成运输任务的天数.
21.一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)求v与t的函数关系式及t的取值范围;
(2)客车上午8时从甲地出发.
①客车需在当天14时40分至15时30分(含14时40分与15时30分)间到达乙地,求客车行驶速度v的范围;
②客车能否在当天12时30分前到达乙地 说明理由.
22.某汽车销售商推出分期付款购车促销活动,交付首付款后,余额要在30个月内结清,不计算利息.王先生在活动期间购买了一辆价格为12万元的汽车,交了首付款后平均每月付款y万元,x个月结清,y与x成反比例,其函数图象如图所示.根据图象回答下列问题:
(1)求y关于x的函数解析式,并求出首付款的钱数.
(2)若王先生用20个月结清,则平均每月应付多少万元
(3)如果打算每月付款不超过4 000元,那么王先生至少要用多少个月才能结清余款
23.小明要把一篇文章录入电脑,已知他完成录入的时间y(分钟)与录入文字的速度x(字/分钟)之间的函数关系如图所示.
(1)求y与x之间的函数解析式.
(2)若小明在19:20开始录入,完成录入时间不超过19:35,小明每分钟至少应录入多少字
(3)小明为了收看19:30的《新闻联播》,将原定的录入速度提高了20%,结果比原计划提前2分钟完成,小明实际用了多少分钟完成文章的录入
24.【2021·乐山】通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平衡状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值.
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标不低于36?请说明理由.
25【河北中考】长为300 m的春游队伍,以v(m/s)的速度向东行进,如图①和图②,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围);
(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
中小学教育资源及组卷应用平台
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
1.若三角形框的面积一定,则这个三角形框的底边长a和底边上的高b之间的函数图象大致为( C )
2.为了抵御洪水,长江无为大堤展开加固工程,该工程建设需要运送大量土石方.某运输公司承担了运送总量为108 m3土石方的任务,该运输公司平均运送土石方的速度v(m3/天)与完成运送任务所需时间t(天)之间的函数关系式是( A )
A.v= B.v=108t C.v=t2 D.v=108t2
3.今年,华为公司推出的一款新手机深受消费者推崇,但价格不菲.为此,某电子商城推出分期付款购买新手机的活动,一部售价为9 688元的新手机,前期付款2 000元,后期每个月分别付相同的数额,则每个月的付款额y(元)与付款月数x(x为正整数)之间的函数关系式是 ( C )
A.y=+2 000 B.y=-2000 C.y= D.y=
4.用规格为50 cm×50 cm的地板砖密铺客厅恰好需要60块.如果改用规格为a cm×a cm的地板砖y块也恰好能密铺该客厅,那么y与a之间的关系式为( A )
A.y= B.y= C.y=150 000a2 D.y=150 000a
5.【2021·宜昌】某气球内充满了一定质量m的气体,当温度不变时,气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=,能够反映两个变量p和V函数关系的图象是( B )
6.如图,一张正方形的纸片,剪去两个一样的小矩形得到一个“E”图案,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y与x的函数图象是( A )
7.攀登珠穆朗玛峰的探险者一般携带一种容积为5 L的氧气瓶,一探险者的吸氧速度每小时不少于1 L,但不多于5 L,则表示此人的吸氧速度x(单位:L/h)与氧气可供使用的时间y(单位:h)的函数图象是( D )
【点拨】氧气瓶容积一定,则吸氧速度x与氧气可供使用的时间y成反比例函数关系.由题意知y=,又1≤x≤5,所以1≤y≤5.故选D.
【答案】D
8.实验证实,放射性物质在放出射线后,质量将减少,减少的速度开始较快,后来较慢,实际上,物质所剩的质量与时间成某种函数关系.如图为表示镭的放射规律的函数图象,据此可计算32 mg镭缩减为1 mg所用的时间大约是( C )
A.4860年 B.6480年 C.8100年 D.9720年
【点拨】由题图可知:1620年时,镭质量缩减为原来的,再经过1620年,即当3240年时,镭质量缩减为原来的=,再经过1620×2=3240年,即当4860年时,镭质量缩减为原来的=,
∴再经过1620×4=6480年,
即当8100年时,镭质量缩减为原来的=,
此时32×=1(mg),
故选C.
9.【2021·贵阳实验二中校级月考】已知甲、乙两地相距30千米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/时)的函数图象为( D )
10.为了响应习总书记“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2022年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分.下列选项错误的是( C )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
第10题图 第11题图 第12题图
11.【2021·太原期末改编】某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=(k≠0)的一部分,则当x=16时,大棚内的温度为( C )
A.18 ℃ B.15.5 ℃ C.13.5 ℃ D.12 ℃
12.如图①,在矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图②所示,等腰直角三角形AEF的斜边EF过点C,M为EF的中点,则下列结论正确的是( C )
A.当x=3时,EC<EM B.当x=9时,EC<EM
C.当x增大时,BE·DF的值不变 D.当x增大时,EC·CF的值增大
【点拨】易知△BEC和△DCF都是等腰直角三角形.观察反比例函数图象可知当x=3时,y=3,则反比例函数的解析式为y=.
A选项,当x=3时,y=3,即BC=CD=3,所以CE=BC=3,CF=CD=3,所以C点与M点重合,则EC=EM,故A错误.
B选项,当x=9时,y=1,即BC=9,CD=1,所以EC=9,EF=10.所以EM=5.所以EC>EM,故B错误.
C选项,BE·DF=BC·CD=xy=9,即BE·DF的值不变,故C正确.
D选项,因为EC·CF=x·y=2·xy=18,故EC·CF为定值,故D错误.
二、填空题
13.如图是一个蓄水池每小时的排水量V(m3/h)与排完水池中的水所用时间t(h)之间的函数关系图象,若要5 h排完水池中的水,则每小时的排水量应为____m3/h.
【答案】9.6
第13题图 第15题图 第17题图 第18题图
14.把一个长、宽、高分别为3 cm,2 cm,1 cm的长方体铜块铸成一个圆柱体铜块,则该圆柱体铜块的底面积S(cm2)与高h(cm)之间的函数关系式为 S= .
15.一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式t=,其图象为如图所示的一段曲线,且端点为A(40,1)和B(m,0.5).若行驶速度不得超过60 km/h,则汽车通过该路段最少需要时间为 h.
16.某商品售价y(元/件)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比例,根据表格写出y与x的函数关系式为 y=+5 .
售价y/(元·件-1) 11 10
月需求量x/件 100 120
17.随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速低于20千米/时时,交通就会拥堵.为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是 .
【答案】0
【答案】48
三、解答题
19.某养鱼专业户准备挖一个面积为2000米2的长方形鱼塘.
(1)求鱼塘的长y(米)关于宽x(米)的函数解析式.
(2)由于受场地的限制,鱼塘的宽最多只能挖20米,当鱼塘的宽是20米时,鱼塘的长为多少米
解:(1)由长方形面积为2000米2,得到xy=2000,即y=.
(2)当x=20时,y==100,
答:当鱼塘的宽是20米时,鱼塘的长为100米.
20.某物流公司要把3000吨货物从M市运到W市.(每日的运输量为固定值)
(1)从运输开始,每天运输的货物吨数y(吨)与运输时间x(天)之间有怎样的函数关系式
(2)因受到沿线道路改扩建工程影响,实际每天的运输量比原计划少20%,以致推迟1天完成运输任务.求原计划完成运输任务的天数.
解:(1)由题意,得xy=3000,∴y=(x>0).
(2)设原计划x天完成运输任务.
根据题意,得,解得x=4.
经检验x=4是原分式方程的根,且符合题意.
答:原计划4天完成运输任务.
21.一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)求v与t的函数关系式及t的取值范围;
(2)客车上午8时从甲地出发.
①客车需在当天14时40分至15时30分(含14时40分与15时30分)间到达乙地,求客车行驶速度v的范围;
②客车能否在当天12时30分前到达乙地 说明理由.
解:(1)设v与t的函数关系式为v=(k≠0),
将(5,120)代入v=,
解得k=600,
∴v与t的函数关系式为v=(5≤t≤10).
(2)①当t=时,v=80,
∴客车行驶速度v的范围为80≤v≤90.
②不能.
理由:若客车在当天12时30分到达,则t=4.5<5,
而5≤t≤10,故客车不能在当天12时30分前到达乙地.
22.某汽车销售商推出分期付款购车促销活动,交付首付款后,余额要在30个月内结清,不计算利息.王先生在活动期间购买了一辆价格为12万元的汽车,交了首付款后平均每月付款y万元,x个月结清,y与x成反比例,其函数图象如图所示.根据图象回答下列问题:
(1)求y关于x的函数解析式,并求出首付款的钱数.
(2)若王先生用20个月结清,则平均每月应付多少万元
(3)如果打算每月付款不超过4 000元,那么王先生至少要用多少个月才能结清余款
解:(1)设y关于x的函数解析式为y=(k≠0),
把(5,1.8)代入y=(k≠0),得k=9,
∴y=(0<x≤30,且x为正整数).
∴余额为9万元,12-9=3(万元),
∴首付款为3万元.
(2)当x=20时,y==0.45.
∴平均每月应付0.45万元.
(3)由题意,知≤0.4,∴x≥22.5.
∵x为正整数,∴王先生至少要用23个月才能结清余款.
23.小明要把一篇文章录入电脑,已知他完成录入的时间y(分钟)与录入文字的速度x(字/分钟)之间的函数关系如图所示.
(1)求y与x之间的函数解析式.
(2)若小明在19:20开始录入,完成录入时间不超过19:35,小明每分钟至少应录入多少字
(3)小明为了收看19:30的《新闻联播》,将原定的录入速度提高了20%,结果比原计划提前2分钟完成,小明实际用了多少分钟完成文章的录入
解:(1)设y关于x的函数解析式为y=(k≠0).
把点(150,10)代入,得10=,∴k=1500,
∴y与x之间的函数解析式为y=.
(2)∵k>0,在第一象限内,y随x的增大而减小,
∴当y≤15时,x≥100.
答:小明每分钟至少录入100字.
(3)设小明实际用了t分钟,则原计划用时(t+2)分钟.
由题意,得(1+20%)×,解得t=10,
经检验t=10是原分式方程的解,且符合题意.
答:小明实际用了10分钟完成文章的录入.
24.【2021·乐山】通过实验研究发现:初中生在数学课上听课注意力指标随上课时间的变化而变化,上课开始时,学生兴趣激增,中间一段时间,学生的兴趣保持平衡状态,随后开始分散.学生注意力指标y随时间x(分钟)变化的函数图象如图所示,当0≤x<10和10≤x<20时,图象是线段;当20≤x≤45时,图象是反比例函数的一部分.
(1)求点A对应的指标值.
解:设当20≤x≤45时,反比例函数的解析式为y=.
将C(20,45)的坐标代入,得45=,解得k=900.
∴反比例函数的解析式为y=.
当x=45时,y==20,∴D(45,20).
∴A(0,20),即A对应的指标值为20.
(2)张老师在一节课上讲解一道数学综合题需要17分钟,他能否经过适当的安排,使学生在听这道综合题的讲解时,注意力指标不低于36?请说明理由.
解:设当0≤x<10时,线段AB的解析式为y=mx+n.
将A(0,20),B(10,45)的坐标代入,
得解得
∴线段AB的解析式为y=x+20(0≤x<10).
当y≥36时,x+20≥36,解得x≥.
由(1)得反比例函数的解析式为y=.
当y≥36时,≥36,解得x≤25,
∴当≤x≤25时,注意力指标不低于36.
∵25-=>17,∴张老师能经过适当的安排,使学生在听这道综合题的讲解时,注意力指标不低于36.
25【河北中考】长为300 m的春游队伍,以v(m/s)的速度向东行进,如图①和图②,当队伍排尾行进到位置O时,在排尾处的甲有一物品要送到排头,送到后立即返回排尾,甲的往返速度均为2v(m/s),当甲返回排尾后,他及队伍均停止行进.设排尾从位置O开始行进的时间为t(s),排头与O的距离为S头(m).
(1)当v=2时,解答:
①求S头与t的函数关系式(不写t的取值范围);
②当甲赶到排头位置时,求S头的值;在甲从排头返回到排尾过程中,设甲与位置O的距离为S甲(m),求S甲与t的函数关系式(不写t的取值范围);
(2)设甲这次往返队伍的总时间为T(s),求T与v的函数关系式(不写v的取值范围),并写出队伍在此过程中行进的路程.
解:(1)①排尾从位置O开始行进的时间为t(s),则排头也离开原排头t(s),
∴S头=2t+300 ②甲从排尾赶到排头的时间为300÷(2v-v)=300÷v=300÷2=150(s),此时S头=2t+300=600(m),甲返回时间为:(t-150)s,
∴S甲=S头-S甲回=2×150+300-4(t-150)=-4t+1200;
因此,S头与t的函数关系式为S头=2t+300,当甲赶到排头位置时,S头的值为600 m;
在甲从排头返回到排尾过程中,S甲与t的函数关系式为S甲=-4t+1200
(2)T=t追及+t返回=+=,在甲这次往返队伍的过程中队伍行进的路程为:v×=400;因此T与v的函数关系式为:T=,此时队伍在此过程中行进的路程为400 m
