青岛版九年级下册数学第五章对函数的再探索5.8二次函数的应用1
文档属性
| 名称 | 青岛版九年级下册数学第五章对函数的再探索5.8二次函数的应用1 |

|
|
| 格式 | zip | ||
| 文件大小 | 191.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-16 08:37:23 | ||
图片预览


文档简介
(共12张PPT)
用待定系数法求二次函数的解析式
y
x
o
课 前 复 习
例 题 选 讲
课 堂 小 结
课 堂 练 习
1、某工厂为了存放材料,需要围一个周长为160米
的矩形场地,问:矩形的长和宽各取多少米,才能使存放场地的面积最大?
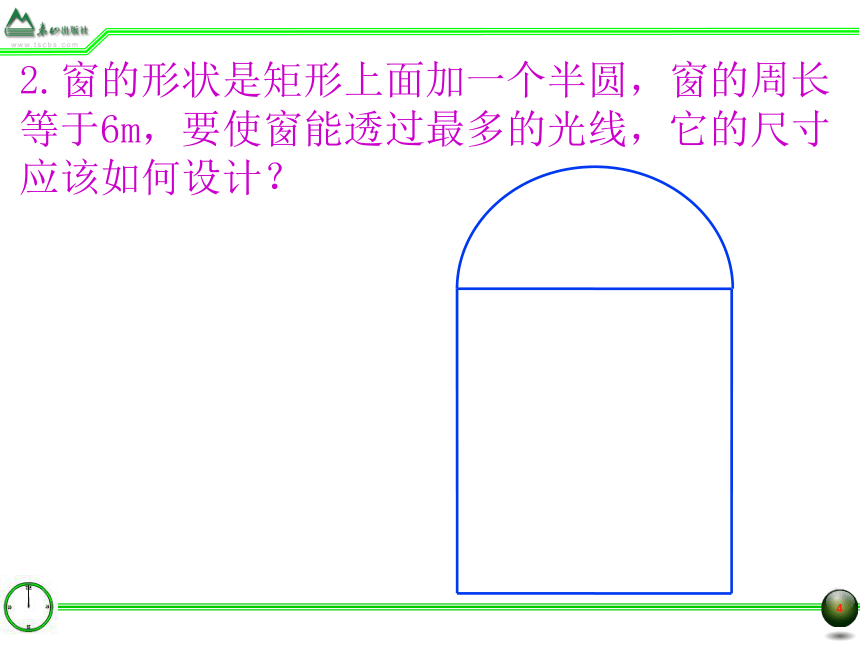
2.窗的形状是矩形上面加一个半圆,窗的周长等于6m,要使窗能透过最多的光线,它的尺寸应该如何设计?
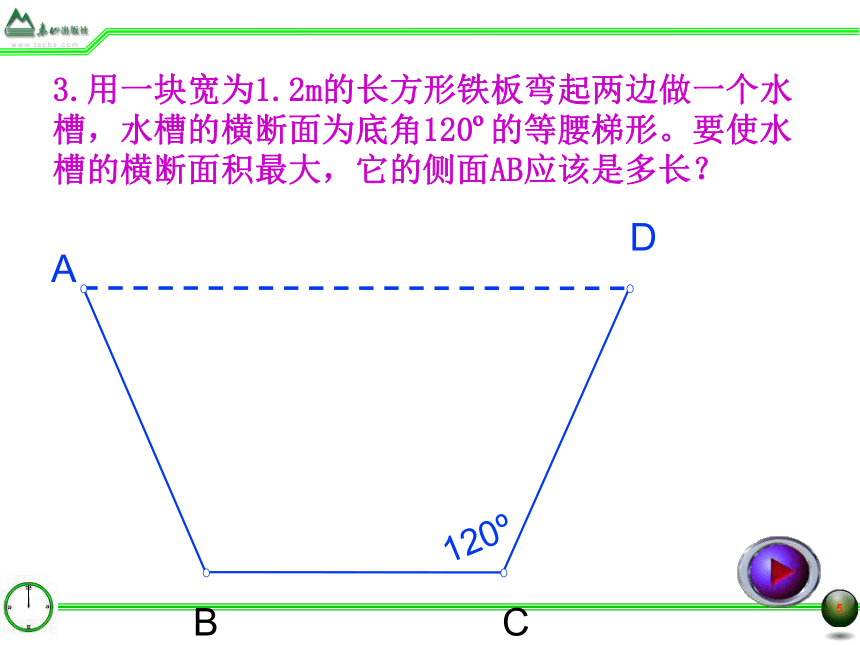
3.用一块宽为1.2m的长方形铁板弯起两边做一个水槽,水槽的横断面为底角120?的等腰梯形。要使水槽的横断面积最大,它的侧面AB应该是多长?
B
C
A
D
120?
4.快艇和轮船分别从A地和C地同时出发,各沿着所指方向航行(如图所示),快艇和轮船的速度分别是每小时40km和每小时16km.已知AC=145km,经过多少时间,快艇和轮船之间的距离最短?(图中AC⊥CD)
D
C
A
145km
5.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施。经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天盈利最多?
如图,公园要建造圆形喷水池,在水池中央垂直于水面处安装一柱子OA,O恰在水面中心,OA=1.25m。由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米。(1)如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(2)若水流喷出的抛物线形状与
(1)相同,水池的半径
为3.5米,要使水流不落到
池外,此时水流的最大高度
应达到多少米?
(精确到0.1米)
某化工材料经销公司购进了一种化工原料共7000千克,购进价格为每千克30元。物价部门规定其销售单价不得高于每千克70元,也不得低于30元。市场调查发现:单价定为70元时,日均销售60千克;单价每降低1元,日均多售出2千克。在销售过程中,每天还要支出其它费用500元(天数不足一天时,按整天计算)。设销售单价为x元,日均获利为y元。
(1)求y关于x的函数关系式,并注明x的取值范围。
(2)将(1)中所求出的函数配方成顶点式,写出顶点坐标。
并指出单价定为多少元时日均获利最多,是多少?
解函数应用题的一般步骤:
设未知数(确定自变量和函数);
找等量关系,列出函数关系式;
化简,整理成标准形式(一次函数、二次函数等);
求自变量取值范围;
利用函数知识,求解(通常是最值问题);
写出结论。
某新建商场设有百货部、服装部和家电部三个经营部,共有190名售货员,计划全商场日营业额(指每天卖出商品所收到的总金额)为60万元,由于营业性质不同,分配到三个部的售货员的人数也就不等,根据经验,各类商品每1万元营业额所需售货员人数如表(1),每1万元营业额所得利润情况如表(2)。商场将计划日营业额分配给三个经营部,设分配给百货部,服装部和家电部的营业额分别为x,y和z(单位:万元,x、y、z都是整数)。(1)请用含x的代数式分别表示y和z;(2)若商场预计每日的总利润为C(万元),且C满足19≤C≤19.7。问商场应如何分配营业额给三个经营部?各应分别安排多少名售货员?
商品
每1万元营业额所需人数
百货类
5
服装类
4
家电类
2
商品
每1万元营业额所得利润
百货类
0.3万元
服装类
0.5万元
家电类
0.2万元
用待定系数法求二次函数的解析式
y
x
o
课 前 复 习
例 题 选 讲
课 堂 小 结
课 堂 练 习
1、某工厂为了存放材料,需要围一个周长为160米
的矩形场地,问:矩形的长和宽各取多少米,才能使存放场地的面积最大?
2.窗的形状是矩形上面加一个半圆,窗的周长等于6m,要使窗能透过最多的光线,它的尺寸应该如何设计?
3.用一块宽为1.2m的长方形铁板弯起两边做一个水槽,水槽的横断面为底角120?的等腰梯形。要使水槽的横断面积最大,它的侧面AB应该是多长?
B
C
A
D
120?
4.快艇和轮船分别从A地和C地同时出发,各沿着所指方向航行(如图所示),快艇和轮船的速度分别是每小时40km和每小时16km.已知AC=145km,经过多少时间,快艇和轮船之间的距离最短?(图中AC⊥CD)
D
C
A
145km
5.某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元,为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施。经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件.
(1)若商场平均每天要盈利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天盈利最多?
如图,公园要建造圆形喷水池,在水池中央垂直于水面处安装一柱子OA,O恰在水面中心,OA=1.25m。由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米。(1)如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流不致落到池外?(2)若水流喷出的抛物线形状与
(1)相同,水池的半径
为3.5米,要使水流不落到
池外,此时水流的最大高度
应达到多少米?
(精确到0.1米)
某化工材料经销公司购进了一种化工原料共7000千克,购进价格为每千克30元。物价部门规定其销售单价不得高于每千克70元,也不得低于30元。市场调查发现:单价定为70元时,日均销售60千克;单价每降低1元,日均多售出2千克。在销售过程中,每天还要支出其它费用500元(天数不足一天时,按整天计算)。设销售单价为x元,日均获利为y元。
(1)求y关于x的函数关系式,并注明x的取值范围。
(2)将(1)中所求出的函数配方成顶点式,写出顶点坐标。
并指出单价定为多少元时日均获利最多,是多少?
解函数应用题的一般步骤:
设未知数(确定自变量和函数);
找等量关系,列出函数关系式;
化简,整理成标准形式(一次函数、二次函数等);
求自变量取值范围;
利用函数知识,求解(通常是最值问题);
写出结论。
某新建商场设有百货部、服装部和家电部三个经营部,共有190名售货员,计划全商场日营业额(指每天卖出商品所收到的总金额)为60万元,由于营业性质不同,分配到三个部的售货员的人数也就不等,根据经验,各类商品每1万元营业额所需售货员人数如表(1),每1万元营业额所得利润情况如表(2)。商场将计划日营业额分配给三个经营部,设分配给百货部,服装部和家电部的营业额分别为x,y和z(单位:万元,x、y、z都是整数)。(1)请用含x的代数式分别表示y和z;(2)若商场预计每日的总利润为C(万元),且C满足19≤C≤19.7。问商场应如何分配营业额给三个经营部?各应分别安排多少名售货员?
商品
每1万元营业额所需人数
百货类
5
服装类
4
家电类
2
商品
每1万元营业额所得利润
百货类
0.3万元
服装类
0.5万元
家电类
0.2万元
