人教版数学九年级上册24.1.3弧、弦、圆心角 课件(共23张PPT)
文档属性
| 名称 | 人教版数学九年级上册24.1.3弧、弦、圆心角 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 391.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 16:17:09 | ||
图片预览





文档简介
(共23张PPT)
24.1.3弧、弦、圆心角
第二十四章 圆
圆是轴对称图形吗?它的对称轴是什么?
复习
1.我能说出圆的对称性,并识别圆心角.
2. 我能探索出弧、弦、圆心角的关系.并利用它解决圆中的计算、证明.
学习目标
把一个圆形纸片绕圆心旋转180度,观察:
1、所得图形与原图形重合吗?
2、圆是中心对称图形吗 它的对称中心在哪里?
如果把这个圆形纸片绕圆心旋转任意度数还能与原图形重合吗?
结论:圆是中心对称图形,它的对称中心是圆心。圆绕圆心旋转任意一个角度都能与原图形重合。
问题引入
·
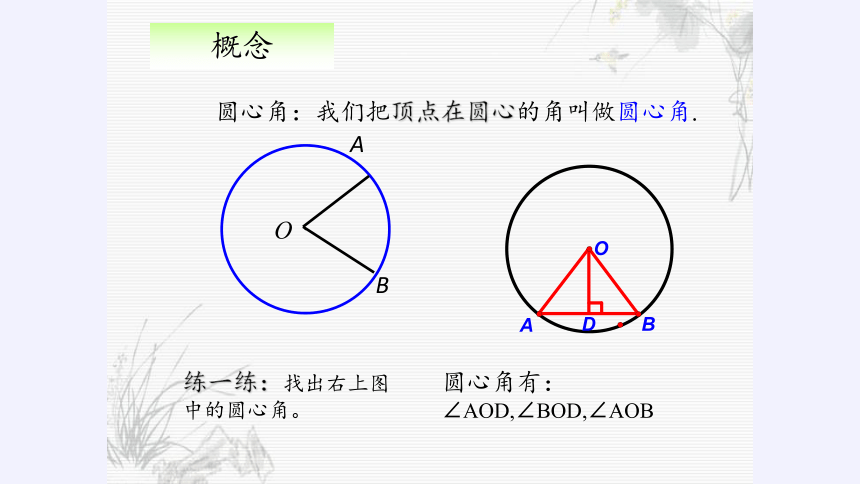
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
概念
练一练:找出右上图中的圆心角。
圆心角有:∠AOD,∠BOD,∠AOB
任意给一个圆心角,对应出现三个量:
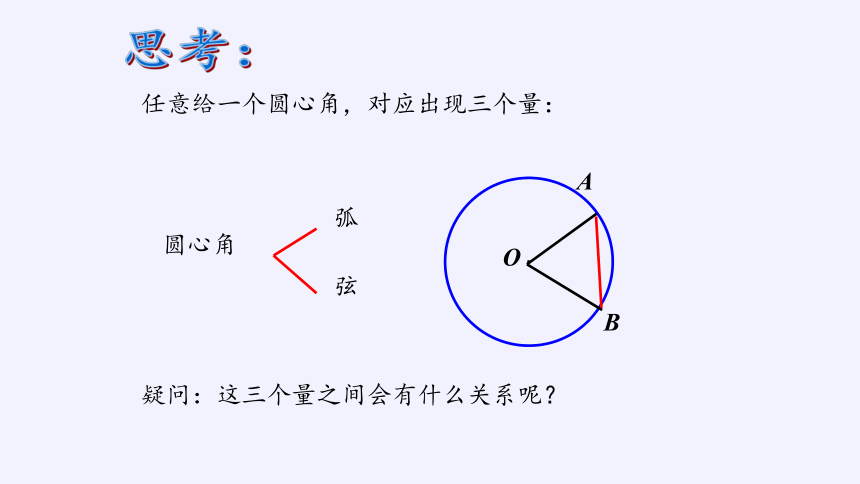
圆心角
弧
弦
·
O
B
A
思考:
疑问:这三个量之间会有什么关系呢?
·
O
A
B
·
O
A
B
A′
B′
A′
B′
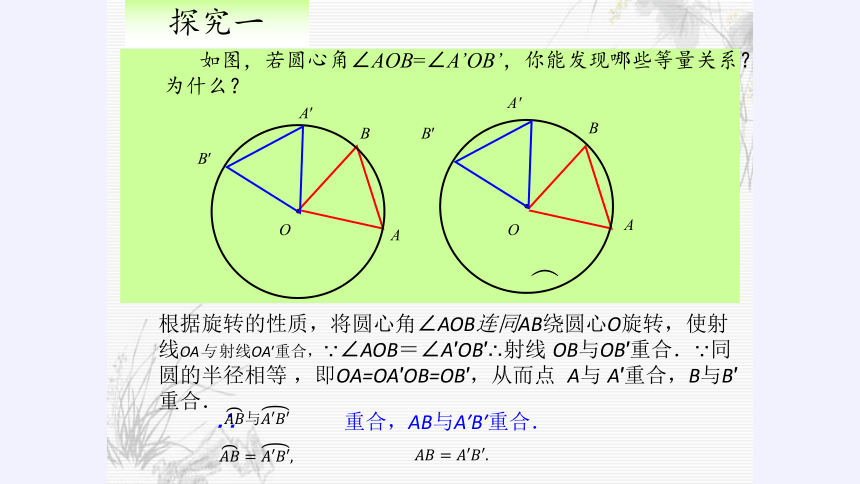
如图,若圆心角∠AOB=∠A’OB’,你能发现哪些等量关系?为什么?
探究一
∴ 重合,AB与A′B′重合.
根据旋转的性质,将圆心角∠AOB连同AB绕圆心O旋转,使射线OA与 射线OA′重合,∵∠AOB=∠A′OB′∴射线 OB与OB′重合.∵同圆的半径相等 ,即OA=OA′OB=OB′,从而点 A与 A′重合,B与B′重合.
︵
·
O
A
B
·
O
A
B
A′
B′
A′
B′
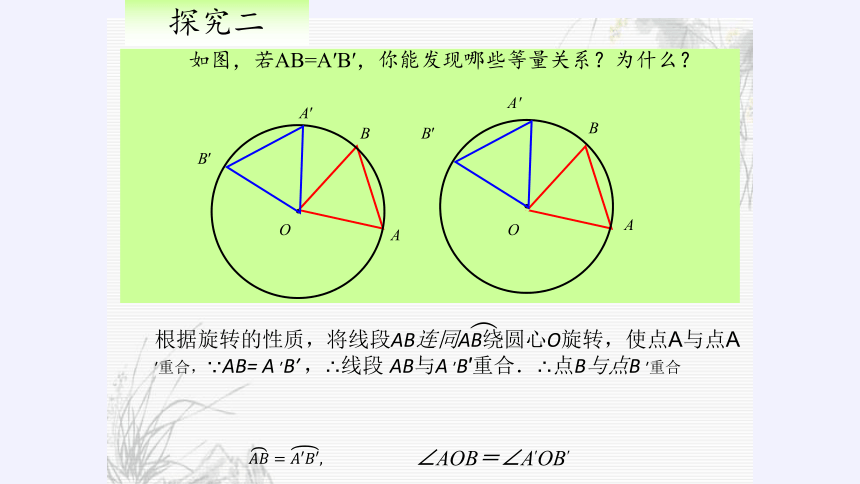
如图,若AB=A′B′,你能发现哪些等量关系?为什么?
探究二
∠AOB=∠A′OB′
根据旋转的性质,将线段AB连同AB绕圆心O旋转,使点A与点A ′重合,∵AB= A ′B′ ,∴线段 AB与A ′B′重合.∴点B与点B ′重合
︵
在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦________;
在同圆或等圆中,相等的弦所对的圆心角______,所对的弧_________.
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
相等
相等
相等
相等
归纳
说一说
·
O
B′
A′
B
A
·
O
·
B′
O
·
A′
B′
O
·
B
A′
B′
O
请利用右图用数学语言叙述一下我们刚学的三条定理。
1、
2、
3、
O
α
A
B
A1
B1
α
同圆或等圆中,两个圆心角、两个圆心角所对的弧、两个圆心角所对的弦中如果有一组量相等,它们所对应的其余各组量也相等。
等对等定理
延伸:
1°弧
n°
1°
n°弧
∵把圆心角等分成360份,则每一份的圆心角是1 .同时整个圆也被分成了360份.
则每一份这样的弧叫做1 的弧.
这样,1 的圆心角对着1 的弧,
1 的弧对着1 的圆心角.
n 的圆心角对着n 的弧,
n 的弧对着n 的圆心角.
性质:弧的度数和它所对圆心角的度数相等.
(2) 所对的圆心角和 所对的圆 心角相等
在两个圆中,分别有 , 若 的度数和 相等,则有
(1) 和 相等
判断
=
1.在半径相等的⊙O和⊙O 中,AB和A B 所对的圆心
角都是60°.
(1)AB和A B各是多少度
(2)AB和A B 相等吗
(3)在同圆或等圆中,度数相度的弧相等.为什么
2.若把圆5等分,那么每一份弧是多少度 若把圆8等分,那么
每一份弧是多少度
3.圆心到弦的距离叫做这条弦的弦心距.求证:在同圆或等圆中,相等的圆心角所对的弦的弦心距相等.
⌒
⌒
⌒
⌒
⌒
⌒
试一试
例 1、 如图A ,已知⊙O 的弦 AB 与半径 OE,OF
分别交于点 C,D,且 AC=BD.
求证:(1)OC=OD;
(2)AE=BF.
图 A
例题分析
证明:(1)作 OH⊥AB 交 AB 于点 H,交圆于点 G,
∵OH⊥AB,∴AH=BH.
又∵AC=BD,∴CH=DH.
∴△OCH≌△ODH.
∴OC=OD.
(2)由(1),得∠EOG=∠FOG,∴EG=FG.
又∵AG=BG,∴AE=BF.
例2、游乐园的大观览车半径为 26 米,如图 B所示,
已知观览车绕圆心 O 顺时针作匀速运动,旋转一周用 12 分钟.
小芳从观览车的最低处(底面 A 处)乘车,问经过 4 分钟后,
(1)试求小芳随观览车绕圆心 O 顺时针旋转的度数;
(2)此时,小芳距地面 CD 的高度是多少米?
图 B
例题分析
解:∵观览车绕圆心 O 顺时针作匀速运动,旋转一周用12
分钟,
∴经过 4 分钟后,旋转了
4
12
×360°=120°.
(2)如图B,连接OA,在⊙O 上取点B,使∠AOB=120°,
分别过点 B,O 作 BF⊥CD 于点 F,作 OE⊥BF 于点 E.
∵OB=26,
∴∠BOE=120°-∠EOA=30°,
∴BE=13 米.
则 BF=13+26=39(米).
答:小芳距地面 CD 的高度是 39 米.
图B
O
A
B
C
D
如图,AC与BD为⊙O的两条互 相垂直的直径.
求证:AB=BC=CD=DA;
AB=BC=CD=DA.
⌒
⌒
⌒
⌒
∴ AB=BC=CD=DA
⌒
⌒
⌒
⌒
证明: ∵AC与BD为⊙O的两条互相垂直的直径,
∴∠AOB=∠BOC=∠COD=∠DOA=90
AB=BC=CD=DA(圆心角定理)
拓展延伸
1、如图所示,A,B,C是⊙O上的三点,∠AOB=120°,C是AB的中点,试判断四边形OACB形状,并说明理由.
⌒
思考
思考
如图,已知AB、CD为⊙O的两条弦,
AD=BC, 求证AB=CD
⌒ ⌒
课堂小结
学完本节课,谈谈你的收获
谢 谢
24.1.3弧、弦、圆心角
第二十四章 圆
圆是轴对称图形吗?它的对称轴是什么?
复习
1.我能说出圆的对称性,并识别圆心角.
2. 我能探索出弧、弦、圆心角的关系.并利用它解决圆中的计算、证明.
学习目标
把一个圆形纸片绕圆心旋转180度,观察:
1、所得图形与原图形重合吗?
2、圆是中心对称图形吗 它的对称中心在哪里?
如果把这个圆形纸片绕圆心旋转任意度数还能与原图形重合吗?
结论:圆是中心对称图形,它的对称中心是圆心。圆绕圆心旋转任意一个角度都能与原图形重合。
问题引入
·
圆心角:我们把顶点在圆心的角叫做圆心角.
O
B
A
概念
练一练:找出右上图中的圆心角。
圆心角有:∠AOD,∠BOD,∠AOB
任意给一个圆心角,对应出现三个量:
圆心角
弧
弦
·
O
B
A
思考:
疑问:这三个量之间会有什么关系呢?
·
O
A
B
·
O
A
B
A′
B′
A′
B′
如图,若圆心角∠AOB=∠A’OB’,你能发现哪些等量关系?为什么?
探究一
∴ 重合,AB与A′B′重合.
根据旋转的性质,将圆心角∠AOB连同AB绕圆心O旋转,使射线OA与 射线OA′重合,∵∠AOB=∠A′OB′∴射线 OB与OB′重合.∵同圆的半径相等 ,即OA=OA′OB=OB′,从而点 A与 A′重合,B与B′重合.
︵
·
O
A
B
·
O
A
B
A′
B′
A′
B′
如图,若AB=A′B′,你能发现哪些等量关系?为什么?
探究二
∠AOB=∠A′OB′
根据旋转的性质,将线段AB连同AB绕圆心O旋转,使点A与点A ′重合,∵AB= A ′B′ ,∴线段 AB与A ′B′重合.∴点B与点B ′重合
︵
在同圆或等圆中,相等的弧所对的圆心角_____, 所对的弦________;
在同圆或等圆中,相等的弦所对的圆心角______,所对的弧_________.
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
相等
相等
相等
相等
归纳
说一说
·
O
B′
A′
B
A
·
O
·
B′
O
·
A′
B′
O
·
B
A′
B′
O
请利用右图用数学语言叙述一下我们刚学的三条定理。
1、
2、
3、
O
α
A
B
A1
B1
α
同圆或等圆中,两个圆心角、两个圆心角所对的弧、两个圆心角所对的弦中如果有一组量相等,它们所对应的其余各组量也相等。
等对等定理
延伸:
1°弧
n°
1°
n°弧
∵把圆心角等分成360份,则每一份的圆心角是1 .同时整个圆也被分成了360份.
则每一份这样的弧叫做1 的弧.
这样,1 的圆心角对着1 的弧,
1 的弧对着1 的圆心角.
n 的圆心角对着n 的弧,
n 的弧对着n 的圆心角.
性质:弧的度数和它所对圆心角的度数相等.
(2) 所对的圆心角和 所对的圆 心角相等
在两个圆中,分别有 , 若 的度数和 相等,则有
(1) 和 相等
判断
=
1.在半径相等的⊙O和⊙O 中,AB和A B 所对的圆心
角都是60°.
(1)AB和A B各是多少度
(2)AB和A B 相等吗
(3)在同圆或等圆中,度数相度的弧相等.为什么
2.若把圆5等分,那么每一份弧是多少度 若把圆8等分,那么
每一份弧是多少度
3.圆心到弦的距离叫做这条弦的弦心距.求证:在同圆或等圆中,相等的圆心角所对的弦的弦心距相等.
⌒
⌒
⌒
⌒
⌒
⌒
试一试
例 1、 如图A ,已知⊙O 的弦 AB 与半径 OE,OF
分别交于点 C,D,且 AC=BD.
求证:(1)OC=OD;
(2)AE=BF.
图 A
例题分析
证明:(1)作 OH⊥AB 交 AB 于点 H,交圆于点 G,
∵OH⊥AB,∴AH=BH.
又∵AC=BD,∴CH=DH.
∴△OCH≌△ODH.
∴OC=OD.
(2)由(1),得∠EOG=∠FOG,∴EG=FG.
又∵AG=BG,∴AE=BF.
例2、游乐园的大观览车半径为 26 米,如图 B所示,
已知观览车绕圆心 O 顺时针作匀速运动,旋转一周用 12 分钟.
小芳从观览车的最低处(底面 A 处)乘车,问经过 4 分钟后,
(1)试求小芳随观览车绕圆心 O 顺时针旋转的度数;
(2)此时,小芳距地面 CD 的高度是多少米?
图 B
例题分析
解:∵观览车绕圆心 O 顺时针作匀速运动,旋转一周用12
分钟,
∴经过 4 分钟后,旋转了
4
12
×360°=120°.
(2)如图B,连接OA,在⊙O 上取点B,使∠AOB=120°,
分别过点 B,O 作 BF⊥CD 于点 F,作 OE⊥BF 于点 E.
∵OB=26,
∴∠BOE=120°-∠EOA=30°,
∴BE=13 米.
则 BF=13+26=39(米).
答:小芳距地面 CD 的高度是 39 米.
图B
O
A
B
C
D
如图,AC与BD为⊙O的两条互 相垂直的直径.
求证:AB=BC=CD=DA;
AB=BC=CD=DA.
⌒
⌒
⌒
⌒
∴ AB=BC=CD=DA
⌒
⌒
⌒
⌒
证明: ∵AC与BD为⊙O的两条互相垂直的直径,
∴∠AOB=∠BOC=∠COD=∠DOA=90
AB=BC=CD=DA(圆心角定理)
拓展延伸
1、如图所示,A,B,C是⊙O上的三点,∠AOB=120°,C是AB的中点,试判断四边形OACB形状,并说明理由.
⌒
思考
思考
如图,已知AB、CD为⊙O的两条弦,
AD=BC, 求证AB=CD
⌒ ⌒
课堂小结
学完本节课,谈谈你的收获
谢 谢
同课章节目录
