青岛版九年级下册数学第五章对函数的再探索5.9用图象法解一元二次方程
文档属性
| 名称 | 青岛版九年级下册数学第五章对函数的再探索5.9用图象法解一元二次方程 |  | |
| 格式 | zip | ||
| 文件大小 | 714.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-16 08:46:35 | ||
图片预览




文档简介
(共12张PPT)
同学们,
再见!
秦切出版
www.tscscom
观察与思考
观察抛物线y=x2-2x-3(图5-26).思考下面
的问题
由于在画图和观察过程中
存在误差,所以得到的往往是
元二次方程根的近似值
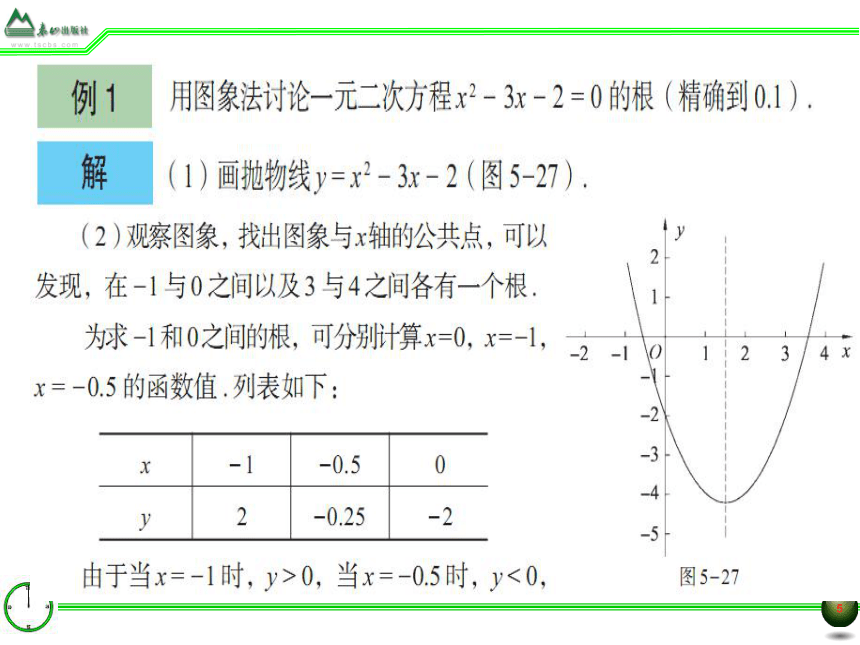
例1用图象法讨论一元二次方程x2-3x-2=0的根(精确到01)
解(1)画抛物线y=x2-3x-2(图5-27)
(2)观察图象,找出图象与x轴的公共点,可以
发现,在-1与0之间以及3与4之间各有一个根
为求-1和0之间的根,可分别计算x=0,x=+1,210
x=-0.5的函数值.列表如
0.5
0
0.25
2
由于当x=-1时,y>0,当x=-0.5时,y<0
图5-27
(4)一元二次方程x2-2x-3=0的根和抛物线y=x2-2x-3与x轴的公共
点的横坐标有什么关系?
(5)你能猜想一元二次方程ax2+bx+c=0的实数根和抛物线y=ax2+bx+c
与x轴公共点的横坐标的关系吗?
6)你能通过画抛物线y=ax2+bx+c的方法讨论方程ax2+bx+c=0的根
所以方程的根在-1和-0.5之间.可再将-1和-0.5之间分为5等份,每个分点
作为x值,利用计算器求出所对应的函数值,列表
1.0
0.9
0.8
0.7
0.6
0.5
1.51
1.04
0.59
0.16
0.25
可以看出,这个根在-0.6和-0.5之间.由于本题要求精确到0.1,所以可
将-0.6或-0.5看作二次方程x2-3x-2=0根的近似值
同样地,可以求出一元二次方程x2-3x-2=0的另一个根的近似值.列表得
3.0
3.5
3.6
3.7
3.8
3.9
4.0
0.25
0.16
0.59
1.04
1.51
由上表可见,方程的这个根在3.5和3.6之间,所以可以将3.5或3.6看作
元二次方程x2-3x-2=0根的近似值(精确到0.1
例2用图象法讨论一元二次方程x2-2x+3=0的根
解(1)画出抛物线y=x2-2x+3(图5-28)
(2)由于图象与x轴没有公共点,所以一元二次方程x2-2x+3=0没有实
根
泰山出版社
图5-29
1)抛物线与x轴有几个公共点?交点的坐标分别
是什么
(2)当x取何值时,函数y=x2-2x-3的值是0?
(3)一元二次方程x2-2x-3=0有没有根?如果
有根,它的根是什么?
2
2
12
2
图5-26
同学们,
再见!
秦切出版
www.tscscom
观察与思考
观察抛物线y=x2-2x-3(图5-26).思考下面
的问题
由于在画图和观察过程中
存在误差,所以得到的往往是
元二次方程根的近似值
例1用图象法讨论一元二次方程x2-3x-2=0的根(精确到01)
解(1)画抛物线y=x2-3x-2(图5-27)
(2)观察图象,找出图象与x轴的公共点,可以
发现,在-1与0之间以及3与4之间各有一个根
为求-1和0之间的根,可分别计算x=0,x=+1,210
x=-0.5的函数值.列表如
0.5
0
0.25
2
由于当x=-1时,y>0,当x=-0.5时,y<0
图5-27
(4)一元二次方程x2-2x-3=0的根和抛物线y=x2-2x-3与x轴的公共
点的横坐标有什么关系?
(5)你能猜想一元二次方程ax2+bx+c=0的实数根和抛物线y=ax2+bx+c
与x轴公共点的横坐标的关系吗?
6)你能通过画抛物线y=ax2+bx+c的方法讨论方程ax2+bx+c=0的根
所以方程的根在-1和-0.5之间.可再将-1和-0.5之间分为5等份,每个分点
作为x值,利用计算器求出所对应的函数值,列表
1.0
0.9
0.8
0.7
0.6
0.5
1.51
1.04
0.59
0.16
0.25
可以看出,这个根在-0.6和-0.5之间.由于本题要求精确到0.1,所以可
将-0.6或-0.5看作二次方程x2-3x-2=0根的近似值
同样地,可以求出一元二次方程x2-3x-2=0的另一个根的近似值.列表得
3.0
3.5
3.6
3.7
3.8
3.9
4.0
0.25
0.16
0.59
1.04
1.51
由上表可见,方程的这个根在3.5和3.6之间,所以可以将3.5或3.6看作
元二次方程x2-3x-2=0根的近似值(精确到0.1
例2用图象法讨论一元二次方程x2-2x+3=0的根
解(1)画出抛物线y=x2-2x+3(图5-28)
(2)由于图象与x轴没有公共点,所以一元二次方程x2-2x+3=0没有实
根
泰山出版社
图5-29
1)抛物线与x轴有几个公共点?交点的坐标分别
是什么
(2)当x取何值时,函数y=x2-2x-3的值是0?
(3)一元二次方程x2-2x-3=0有没有根?如果
有根,它的根是什么?
2
2
12
2
图5-26
