人教版 九年级 上册 24.1.3弧、弦、圆心角 课件(1课时 28张ppt)
文档属性
| 名称 | 人教版 九年级 上册 24.1.3弧、弦、圆心角 课件(1课时 28张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 973.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-10 17:51:42 | ||
图片预览




文档简介
(共28张PPT)
弧、弦、圆心角
探究
剪一个圆形纸片,把它绕圆心旋转180°,所得的图形与原图形重合吗?
重合
由此你得到什么结论?
圆是中心对称图形,对称中心就是圆心.
把圆绕圆心旋转任意一个角度呢?
不管旋转多少度,圆都与自身重合.
接下来,我们就利用圆的旋转不变性继续探究圆的性质.
圆心角
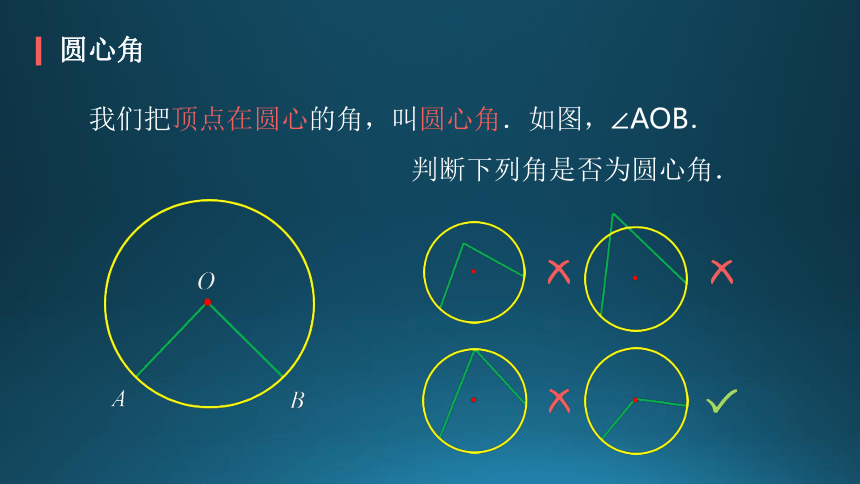
我们把顶点在圆心的角,叫圆心角.如图,∠AOB.
判断下列角是否为圆心角.
圆心角
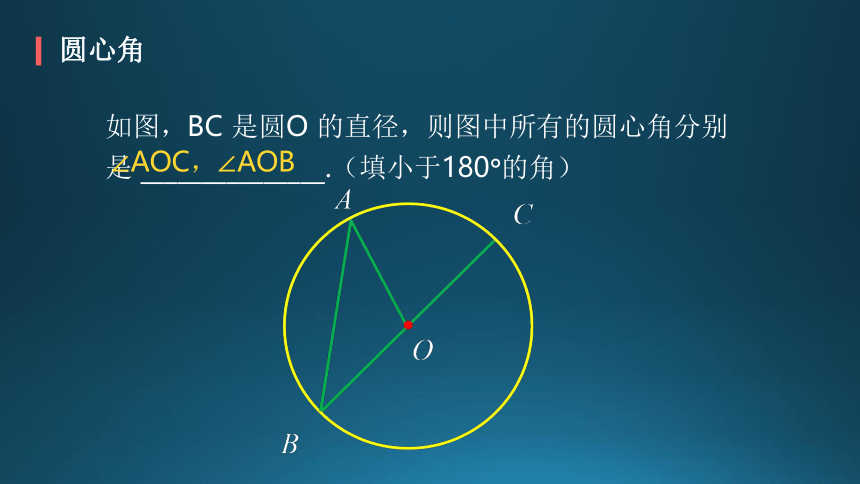
如图,BC 是圆O 的直径,则图中所有的圆心角分别是 _______________.(填小于180°的角)
∠AOC,∠AOB
探究
下面我们一起来研究在同一圆中,圆心角与它所对的弦、弧有什么关系?
如图,在圆O 中,当圆心角∠AOB =∠A’OB ’时,
相等
它们所对的弦AB 和A’B ’相等吗?
相等
你知道这是为什么吗?
因为圆具有旋转不变性.
它们所对的弧 相等吗?
探究
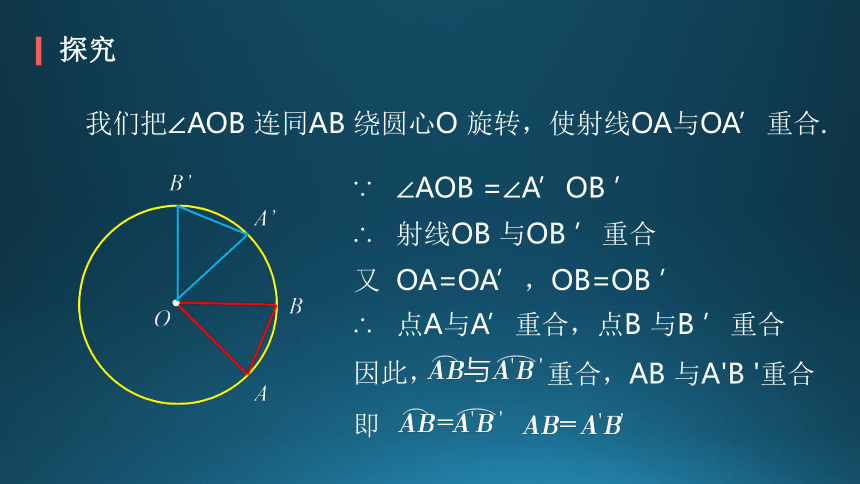
我们把∠AOB 连同AB 绕圆心O 旋转,使射线OA与OA’重合.
∵ ∠AOB =∠A’OB ’
∴ 射线OB 与OB ’重合
又 OA=OA’,OB=OB ’
∴ 点A与A’重合,点B 与B ’重合
即
因此,
重合,AB 与A'B '重合
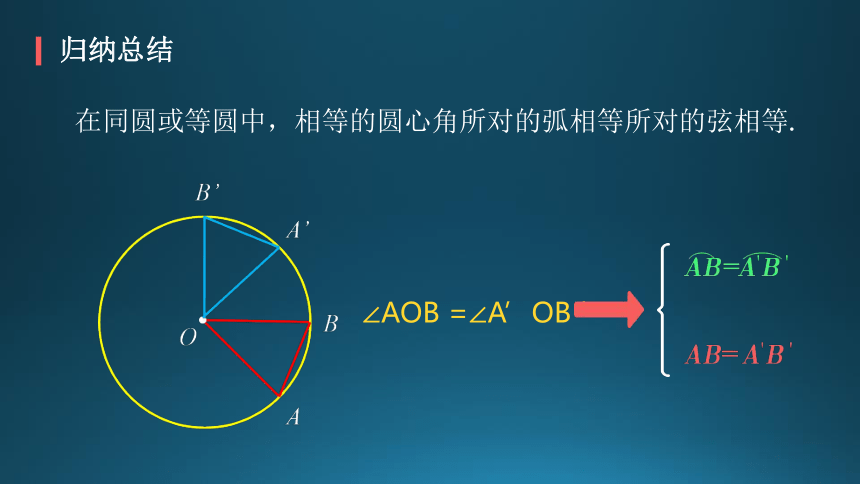
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等.
归纳总结
∠AOB =∠A’OB ’
在同圆或等圆中,如果轮换下面三组条件:①圆心角相等;②弧相等;③弦相等.你能得到什么结论?与同伴交流你的想法和理由.
归纳总结
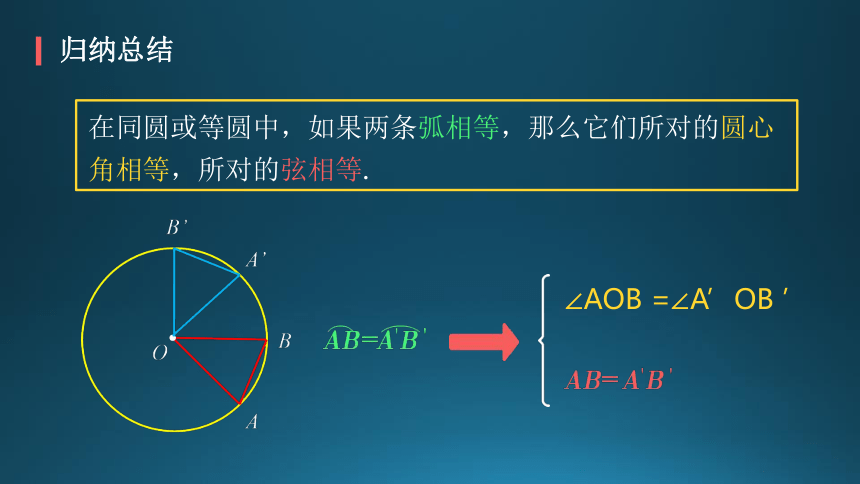
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等.
归纳总结
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
∠AOB =∠A’OB ’
归纳总结
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等.
∠AOB =∠A’OB ’
归纳总结
在同圆或等圆中,下面三组条件:①圆心角相等;②弧相等;③弦相等只要有一组相等,其余的两组也相等.
∠AOB =∠A’OB ’
∠AOB =∠A’OB ’
∠AOB =∠A’OB ’
练习
如图,在圆O 中, , ∠ACB =60° . 求证:∠AOB =∠BOC =∠AOC .
∴ AB =AC,△ABC 是等腰三角形
又 ∠ACB =60°
∴ △ABC 是等边三角形,AB =BC =CA
∴ ∠AOB =∠BOC =∠AOC
证明:
1.如图,AB,CD 是圆O 的两条弦.
(1)如果AB =CD,那么_____________,____________;
(2)如果 , 那么_____________,____________;
(3)如果∠AOB =∠COD,那么_________,__________;
(4)如果AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,OE与OF 相等吗?为什么?
练习
练习
2.如图,AB 是圆O 的直径, ,∠COD=35°. 求
∠AOE 的度数.
练习——易错点
下面的说法正确吗 为什么
如图,因为∠AOB =∠A’OB ’,
所以
不正确,在同圆或等圆中,才有相等的圆心角所对弧相等.
练习——计算
如图,在圆O 中, , ∠A=40°,求∠B 的度数 .
答案:70° .
练习
如图:已知OA,OB 是⊙O 中的两条半径,且OA⊥OB,D 是弧AB上的一点,AD 的延长线交OB 延长线于点C .已知∠C =25°,求圆心角∠DOB 的度数.
答案:40°.
练习
如图,已知AB,CD 为圆O 的两条弦, ,求证:AB =CD .
提示:先证明弧相等 .
练习
如图,AB,AC,BC 都是圆O 的弦,且∠CAB =∠CBA .
求证:∠COA=∠COB .
提示:先证弦相等 .
练习
如图D 、A 、C 、B 为⊙O上的点,DC =AB,求证:AD =BC .
提示:先证弧相等.
练习
如图,AB,CD 为⊙O 的两条弦,AB =CD .求证:∠AOC =∠BOD .
提示:先证弧相等.
把圆心角等分成 360 份,则每一份的圆心角是 1°,同时整个圆也被分成了 360 份.则每一份这样的弧叫做 1°的弧.
弧的度数
1°的圆心角对着 1°的弧,1°的弧对着 1°的圆心角.
n°的圆心角对着 n°的弧,n°的弧对着 n°的圆心角.
1°
n°的弧
1°的弧
n°
弧的度数
性质:弧的度数和它所对圆心角的度数相等.
练习
108°
如图,在 O 中,已知AB=BC, =7:6,则∠AOC = ______ .
平行弦所夹弧相等
如图,在⊙O 中,弦AB∥CD,求证: .
提示:连接AO,CO,BO,DO,作OH⊥CD于H,交AB于G .
所知弧求弦长
如图,在圆O 中,弦AB所对的劣弧为圆的 ,圆的半径为4cm,求AB 的长.
提示1:由条件可知,∠AOB =120°
提示2:过点O 作AB 的垂线
答案:
总结
这节课我们学会了什么?
在同圆或等圆中,下面三组条件:①圆心角相等;②弧相等;③弦相等只要有一组相等,其余的两组也相等 .
∠AOB =∠A’OB ’
∠AOB =∠A’OB ’
∠AOB =∠A’OB ’
拓展总结
这节课我们还学会了什么?
1°的圆心角对着 1°的弧,1°的弧对着 1°的圆心角.
n°的圆心角对着 n°的弧,n°的弧对着 n°的圆心角.
性质:弧的度数和它所对圆心角的度数相等 .
弧、弦、圆心角
探究
剪一个圆形纸片,把它绕圆心旋转180°,所得的图形与原图形重合吗?
重合
由此你得到什么结论?
圆是中心对称图形,对称中心就是圆心.
把圆绕圆心旋转任意一个角度呢?
不管旋转多少度,圆都与自身重合.
接下来,我们就利用圆的旋转不变性继续探究圆的性质.
圆心角
我们把顶点在圆心的角,叫圆心角.如图,∠AOB.
判断下列角是否为圆心角.
圆心角
如图,BC 是圆O 的直径,则图中所有的圆心角分别是 _______________.(填小于180°的角)
∠AOC,∠AOB
探究
下面我们一起来研究在同一圆中,圆心角与它所对的弦、弧有什么关系?
如图,在圆O 中,当圆心角∠AOB =∠A’OB ’时,
相等
它们所对的弦AB 和A’B ’相等吗?
相等
你知道这是为什么吗?
因为圆具有旋转不变性.
它们所对的弧 相等吗?
探究
我们把∠AOB 连同AB 绕圆心O 旋转,使射线OA与OA’重合.
∵ ∠AOB =∠A’OB ’
∴ 射线OB 与OB ’重合
又 OA=OA’,OB=OB ’
∴ 点A与A’重合,点B 与B ’重合
即
因此,
重合,AB 与A'B '重合
在同圆或等圆中,相等的圆心角所对的弧相等所对的弦相等.
归纳总结
∠AOB =∠A’OB ’
在同圆或等圆中,如果轮换下面三组条件:①圆心角相等;②弧相等;③弦相等.你能得到什么结论?与同伴交流你的想法和理由.
归纳总结
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等.
归纳总结
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦相等.
∠AOB =∠A’OB ’
归纳总结
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧相等.
∠AOB =∠A’OB ’
归纳总结
在同圆或等圆中,下面三组条件:①圆心角相等;②弧相等;③弦相等只要有一组相等,其余的两组也相等.
∠AOB =∠A’OB ’
∠AOB =∠A’OB ’
∠AOB =∠A’OB ’
练习
如图,在圆O 中, , ∠ACB =60° . 求证:∠AOB =∠BOC =∠AOC .
∴ AB =AC,△ABC 是等腰三角形
又 ∠ACB =60°
∴ △ABC 是等边三角形,AB =BC =CA
∴ ∠AOB =∠BOC =∠AOC
证明:
1.如图,AB,CD 是圆O 的两条弦.
(1)如果AB =CD,那么_____________,____________;
(2)如果 , 那么_____________,____________;
(3)如果∠AOB =∠COD,那么_________,__________;
(4)如果AB=CD,OE⊥AB,OF⊥CD,垂足分别为E,F,OE与OF 相等吗?为什么?
练习
练习
2.如图,AB 是圆O 的直径, ,∠COD=35°. 求
∠AOE 的度数.
练习——易错点
下面的说法正确吗 为什么
如图,因为∠AOB =∠A’OB ’,
所以
不正确,在同圆或等圆中,才有相等的圆心角所对弧相等.
练习——计算
如图,在圆O 中, , ∠A=40°,求∠B 的度数 .
答案:70° .
练习
如图:已知OA,OB 是⊙O 中的两条半径,且OA⊥OB,D 是弧AB上的一点,AD 的延长线交OB 延长线于点C .已知∠C =25°,求圆心角∠DOB 的度数.
答案:40°.
练习
如图,已知AB,CD 为圆O 的两条弦, ,求证:AB =CD .
提示:先证明弧相等 .
练习
如图,AB,AC,BC 都是圆O 的弦,且∠CAB =∠CBA .
求证:∠COA=∠COB .
提示:先证弦相等 .
练习
如图D 、A 、C 、B 为⊙O上的点,DC =AB,求证:AD =BC .
提示:先证弧相等.
练习
如图,AB,CD 为⊙O 的两条弦,AB =CD .求证:∠AOC =∠BOD .
提示:先证弧相等.
把圆心角等分成 360 份,则每一份的圆心角是 1°,同时整个圆也被分成了 360 份.则每一份这样的弧叫做 1°的弧.
弧的度数
1°的圆心角对着 1°的弧,1°的弧对着 1°的圆心角.
n°的圆心角对着 n°的弧,n°的弧对着 n°的圆心角.
1°
n°的弧
1°的弧
n°
弧的度数
性质:弧的度数和它所对圆心角的度数相等.
练习
108°
如图,在 O 中,已知AB=BC, =7:6,则∠AOC = ______ .
平行弦所夹弧相等
如图,在⊙O 中,弦AB∥CD,求证: .
提示:连接AO,CO,BO,DO,作OH⊥CD于H,交AB于G .
所知弧求弦长
如图,在圆O 中,弦AB所对的劣弧为圆的 ,圆的半径为4cm,求AB 的长.
提示1:由条件可知,∠AOB =120°
提示2:过点O 作AB 的垂线
答案:
总结
这节课我们学会了什么?
在同圆或等圆中,下面三组条件:①圆心角相等;②弧相等;③弦相等只要有一组相等,其余的两组也相等 .
∠AOB =∠A’OB ’
∠AOB =∠A’OB ’
∠AOB =∠A’OB ’
拓展总结
这节课我们还学会了什么?
1°的圆心角对着 1°的弧,1°的弧对着 1°的圆心角.
n°的圆心角对着 n°的弧,n°的弧对着 n°的圆心角.
性质:弧的度数和它所对圆心角的度数相等 .
同课章节目录
