湘教版九年级数学下册 1.4二次函数与一元二次方程的联系课件(共35张PPT)
文档属性
| 名称 | 湘教版九年级数学下册 1.4二次函数与一元二次方程的联系课件(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览










文档简介
(共35张PPT)
1.4 二次函数与一元二次方程的联系
第1章 二次函数
知识点
二次函数与一元二次方程的关系
知1-讲
1
1. 二次函数图象与x 轴的交点的横坐标与一元二次方程根的关系一般地,如果二次函数y=ax2+bx+c 的图象与x 轴有两个不同的交点(x1,0),(x2,0),那么一元二次方程ax2+bx+c=0 有两个不相等的实数根x=x1,x=x2.
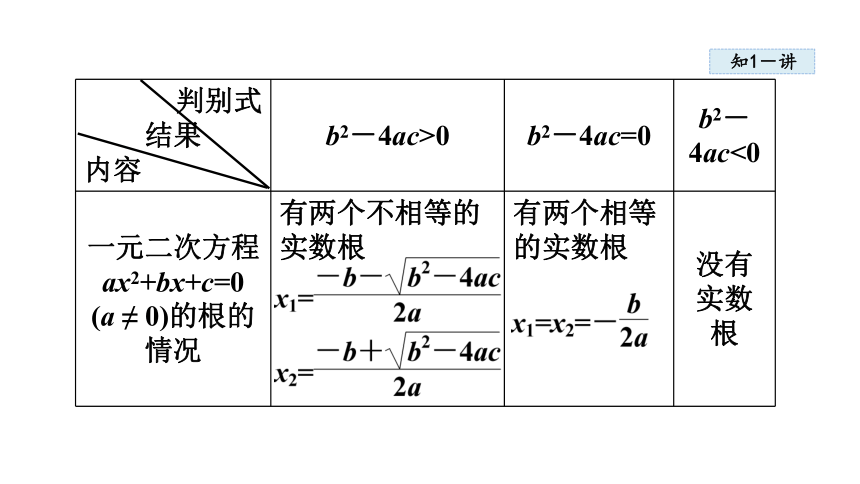
2.二次函数与一元二次方程的联系与区别一元二次方程ax2+bx+c=0(a ≠ 0)与二次函数y=ax2+bx+c(a ≠ 0)二者之间的内在联系与区别,列表如下:
知1-讲
判别式
结果
内容 b2-4ac>0 b2-4ac=0 b2-4ac<0
一元二次方程
ax2+bx+c=0
(a ≠ 0)的根的情况 有两个不相等的实数根
有两个相等
的实数根 没有实数根
知1-讲
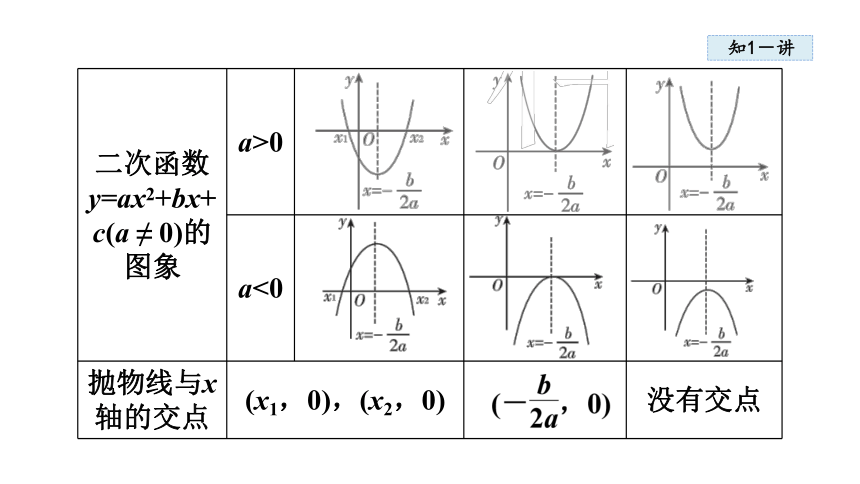
二次函数
y=ax2+bx+c(a ≠ 0)的图象 a>0
a<0
抛物线与x轴的交点 (x1,0),(x2,0) 没有交点
知1-讲
拓宽视野:
1. 已知二次函数y=ax2+bx+c,求当y=m 时自变量x的值,可以解一元二次方程ax2+bx+c=m; 反之,解一元二次方程ax2+bx+c=m 可以看成是已知y=ax2+bx+c的函数值y=m,求自变量x的值. 方程ax2+bx+c=m 的解是抛物线y=ax2+bx+c与直线y=m的公共点的横坐标.
知1-讲
2. 二次函数y=ax2+bx+c 与一元二次方程ax2+bx+c=0 的关系密切,二者可以相互转化. 已知二次函数的值为0,求自变量x的值,可以看作解一元二次方程ax2+bx+c=0; 反过来,解一元二次方程ax2+bx+c=0 可以看作已知二次函数y=ax2+bx+c的函数值为0,求自变量x 的值.
知1-讲
例 1
已知二次函数y=ax2+bx+c 的图象经过(-3,0)与(1,0)两点,关于x的方程ax2+bx+c+m=0(m > 0)有两个根,其中一个根是3.若关于x 的方程ax2+bx+c+n=0(0 < n< m)有两个整数根,则这两个整数根是( )
A. -2,0 B. -4,2 C. -5,3 D. -6,4
B
知1-讲
解:二次函数y=ax2+bx+c 的图象经过(-3,0)与(1,0)两点,即方程ax2+bx+c=0 的两个根是-3和1,由方程ax2+bx+c+m=0 有一个根是3,可得二次函数y=ax2+bx+c 的图象沿着y轴向上平移m个单位后经过点(3,0),则必经过点(-5,0),可得方程ax2+bx+c+m=0 的另一个根为-5. 由0<n<m,可知方程ax2+bx+c+n=0 的两根分别在-5 和-3 之间与1 和3之间,由此判断B 符合该范围.故选B.
知1-讲
解题秘方:由题意可得方程ax2+bx+c=0 的两个根是-3,1,方程左边在原来的基础上加m,可以理解为对应的二次函数的图象沿着y 轴向上平移m个单位, 由此可判断方程的两个根, 进而可判断选项.
方法点拨:
根据二次函数图象沿y轴上移或下移的方法来判断选项.
知2-讲
知识点
利用二次函数的图象求一元二次方程的近似解
2
二次函数y=ax2+bx+c 的图象与x 轴的公共点的横坐标是一元二次方程ax2+bx+c=0 的解,因此可以借助二次函数的图象求一元二次方程的解.
知2-讲
1. 利用二次函数y=ax2+bx+c 的图象与x 轴的公共点求一元二次方程ax2+bx+c=0 的解
(1)作出二次函数y=ax2+bx+c 的图象,确定图象与x 轴公共点的个数,公共点的个数就是方程ax2+bx+c=0 的解的个数.
知2-讲
(2)观察图象,函数图象与x 轴的交点的横坐标就是一元二次方程ax2+bx+c=0 的解,当函数图象与x 轴有两个交点,且交点的横坐标不是整数时,可通过不断缩小解所在的范围估计一元二次方程的解.
(3)交点横坐标即为一元二次方程ax2+bx+c=0 的解.
知2-讲
方法点拨:
估计一元二次方程的解的方法:
在难以读出公共点的坐标时,我们可以通过不断缩小解所在范围估计一元二次方程的解,对于y=ax2+bx+c(a≠0),如果ax21+bx1+c>0, 且ax22+bx2+c<0, 那么在x1与x2之间存在一个解, 取x3= ,若ax23+bx3+c>0, 则取x4= ; 若ax23+bx3+c<0,则取x4= .这样不停地取下去,直到达到所要求的精确度为止.
知2-讲
2. 利用二次函数y=ax2 的图象与直线y=-bx-c 的公共点求方程ax2+bx+c=0 的解
(1)将一元二次方程ax2+bx+c=0 化为ax2=-bx-c 的形式;
(2)在平面直角坐标系中画出抛物线y=ax2 和直线y=-bx-c,并确定抛物线与直线的公共点的坐标;
(3)公共点的横坐标即为一元二次方程ax2+bx+c=0 的解.
知2-讲
例2
利用二次函数的图象求一元二次方程-x2+2x-3=-8 的近似解(结果精确到0.1).
解题秘方一:画出二次函数y=-x2+2x+5 的图象,利用二次函数的图象与x轴的公共点计算方程的近似解.
知2-讲
特别提醒:
用图象法解一元二次方程是数形结合思想的具体应用,通过画函数的图象解一元二次方程是数的直观化的体现,但由于作图或观察存在误差,因此通过这种方法求得的方程的解一般是近似的.
知2-讲
解法一:整理方程,得-x2+2x+5=0.
作函数y=-x2+2x+5 的图象如图1.4-1.
由图象可知,抛物线与x 轴公共点的横坐标分别在-2 和-1,3 和4 之间,即方程-x2+2x-3=-8 的两个实数解分别在-2 和-1,3 和4 之间,用取平均数的方法不断缩小解的取值范围,从而确定方程的近似解.
知2-讲
知2-讲
由图象可知,当x=3 时,y>0;当x=4 时,y<0,
取3 和4 的平均数3.5,当x=3.5 时,y=-0.25,与x=3 时的函数值异号,所以方程的这个解在3 和3.5 之间.
取3 和3.5 的平均数3.25,当x=3.25 时,y=0.937 5,与x=3.5 时的函数值异号,所以方程的这个解在3.25 和3.5 之间.
知2-讲
取3.25 和3.5 的平均数3.375,当x=3.375 时,y=0.359 375,与x=3.5时的函数值异号,所以方程的这个解在3.375 和3.5 之间.
……
由此方法可得到原方程的一个近似解为3.4.
用同样的方法可得到原方程的另一个近似解为-1.4.
所以方程-x2+2x-3=-8 的解为x1≈ -1.4,x2≈ 3.4.
知2-讲
解题秘方二:画出二次函数y=-x2+2x-3 的图象,再画出直线y=-8,利用两图象的公共点求方程的近似解.
知2-讲
解法二:作出函数y=-x2+2x-3 的图象,
再画出直线y=-8,如图1.4-2.
由图象知,方程-x2+2x-3=-8 的解是抛物线
y=-x2+2x-3 与直线y=-8 的公共点的横坐标,一个公共点的横坐标在-2 与-1 之间,另一个公共点的横坐标在3 与4 之间.
同样用取平均数的方法,可得方程-x2+2x-3=-8 的解为x1 ≈ -1.4,x2 ≈ 3.4.
知2-讲
知2-讲
另解:
将原方程变形,得-x2=-2x-5, 画出函数y=-x2和y=-2x-5 的图象, 如图1.4-3.
由图可知,抛物线和直线交于A,B 两点,分别过A,B两点向x轴作垂线,可知A,B两点的横坐标分别约为-1.4和3.4,所以方程-x2+2x-3=-8的解是x1 ≈ -1.4,x2 ≈ 3.4.
知2-讲
知2-讲
解题通法:
用图象法求一元二次方程的近似解:
●先作出相应的二次函数的图象,确定一元二次方程的解的个数,找出公共点的横坐标的大致范围.
●然后利用取平均数的方法缩小解所在的范围,通过反复计算求出满足精确度要求的近似解.
知识点
二次函数y=ax2+bx+c的图象特征与a,b,c的符号关系(拓展点)
知3-讲
3
二次函数y=ax2+bx+c中,a 的符号决定抛物线的开口方向,ab的符号决定抛物线的对称轴的大致位置,c 的符号决定抛物线与y 轴交点的大致位置,b2-4ac 的符号决定抛物线与x轴的交点情况,具体如下表:
知3-讲
符号 图象的特征
a a>0 开口向上
a<0 开口向下
b=0 对称轴为y 轴
ab>0(a,b 同号) 对称轴在y 轴左侧
ab<0(a,b 异号) 对称轴在y 轴右侧
c c=0 图象过原点
c>0 图象与y 轴正半轴相交
c<0 图象与y 轴负半轴相交
b2-4ac b2-4ac=0 图象与x轴有唯一一个交点
b2-4ac>0 图象与x 轴有两个交点
b2-4ac<0 图象与x 轴没有交点
知3-讲
收藏夹:
对于二次函数y=ax2+bx+c:
当x=1 时,y=a+b+c,此时,若y=0,则a+b+c=0;
若y > 0,则a+b+c > 0;
若y < 0,则a+b+c < 0.
当x=-1 时,y=a-b+c,此时,若y=0,则a-b+c=0;
若y > 0,则a-b+c > 0;
若y < 0,则a-b+c < 0.
知3-讲
例 3
已知二次函数y=ax2+bx+c 的图象如图1.4-4,有下列结论:
① a+b+c<0;② a-b+c>0;③ abc>0;④ b2<4ac;⑤ b=2a. 其中正确的结论有( )
A. 4 个
B. 3 个
C. 2 个
D. 1 个
B
知3-讲
解:当x=1 时,对应的函数值y<0,即a+b+c<0,故①正确;
详解:
当x=1时,对应的函数值y=ax2+bx+c=a+b+c,观察图象可知此时抛物线上对应的点在x轴下方,说明此时的函数值y<0,即a+b+c<0.
知3-讲
当x=-1 时,对应的函数值y>0,即a-b+c>0,故②正确;观察图象知抛物线过原点,∴ c=0,∴ abc=0,故③错误;
∵抛物线与x轴有两个交点,∴ b2-4ac>0,即b2 > 4ac, 故④错误;
∵此抛物线的对称轴是直线x=-1,∴ - =-1,
∴ b=2a,故⑤正确.
知3-讲
解题秘方:根据二次函数的图象特征与a,b,c 之间的关系判断.
知3-讲
特别提醒:
抛物线y=ax2+bx+c的对称轴是直线x=- ,判断a,b之间的关系时,往往需要根据抛物线的对称轴的位置来判断.
二次函数与一元二次方程的联系
1.4 二次函数与一元二次方程的联系
第1章 二次函数
知识点
二次函数与一元二次方程的关系
知1-讲
1
1. 二次函数图象与x 轴的交点的横坐标与一元二次方程根的关系一般地,如果二次函数y=ax2+bx+c 的图象与x 轴有两个不同的交点(x1,0),(x2,0),那么一元二次方程ax2+bx+c=0 有两个不相等的实数根x=x1,x=x2.
2.二次函数与一元二次方程的联系与区别一元二次方程ax2+bx+c=0(a ≠ 0)与二次函数y=ax2+bx+c(a ≠ 0)二者之间的内在联系与区别,列表如下:
知1-讲
判别式
结果
内容 b2-4ac>0 b2-4ac=0 b2-4ac<0
一元二次方程
ax2+bx+c=0
(a ≠ 0)的根的情况 有两个不相等的实数根
有两个相等
的实数根 没有实数根
知1-讲
二次函数
y=ax2+bx+c(a ≠ 0)的图象 a>0
a<0
抛物线与x轴的交点 (x1,0),(x2,0) 没有交点
知1-讲
拓宽视野:
1. 已知二次函数y=ax2+bx+c,求当y=m 时自变量x的值,可以解一元二次方程ax2+bx+c=m; 反之,解一元二次方程ax2+bx+c=m 可以看成是已知y=ax2+bx+c的函数值y=m,求自变量x的值. 方程ax2+bx+c=m 的解是抛物线y=ax2+bx+c与直线y=m的公共点的横坐标.
知1-讲
2. 二次函数y=ax2+bx+c 与一元二次方程ax2+bx+c=0 的关系密切,二者可以相互转化. 已知二次函数的值为0,求自变量x的值,可以看作解一元二次方程ax2+bx+c=0; 反过来,解一元二次方程ax2+bx+c=0 可以看作已知二次函数y=ax2+bx+c的函数值为0,求自变量x 的值.
知1-讲
例 1
已知二次函数y=ax2+bx+c 的图象经过(-3,0)与(1,0)两点,关于x的方程ax2+bx+c+m=0(m > 0)有两个根,其中一个根是3.若关于x 的方程ax2+bx+c+n=0(0 < n< m)有两个整数根,则这两个整数根是( )
A. -2,0 B. -4,2 C. -5,3 D. -6,4
B
知1-讲
解:二次函数y=ax2+bx+c 的图象经过(-3,0)与(1,0)两点,即方程ax2+bx+c=0 的两个根是-3和1,由方程ax2+bx+c+m=0 有一个根是3,可得二次函数y=ax2+bx+c 的图象沿着y轴向上平移m个单位后经过点(3,0),则必经过点(-5,0),可得方程ax2+bx+c+m=0 的另一个根为-5. 由0<n<m,可知方程ax2+bx+c+n=0 的两根分别在-5 和-3 之间与1 和3之间,由此判断B 符合该范围.故选B.
知1-讲
解题秘方:由题意可得方程ax2+bx+c=0 的两个根是-3,1,方程左边在原来的基础上加m,可以理解为对应的二次函数的图象沿着y 轴向上平移m个单位, 由此可判断方程的两个根, 进而可判断选项.
方法点拨:
根据二次函数图象沿y轴上移或下移的方法来判断选项.
知2-讲
知识点
利用二次函数的图象求一元二次方程的近似解
2
二次函数y=ax2+bx+c 的图象与x 轴的公共点的横坐标是一元二次方程ax2+bx+c=0 的解,因此可以借助二次函数的图象求一元二次方程的解.
知2-讲
1. 利用二次函数y=ax2+bx+c 的图象与x 轴的公共点求一元二次方程ax2+bx+c=0 的解
(1)作出二次函数y=ax2+bx+c 的图象,确定图象与x 轴公共点的个数,公共点的个数就是方程ax2+bx+c=0 的解的个数.
知2-讲
(2)观察图象,函数图象与x 轴的交点的横坐标就是一元二次方程ax2+bx+c=0 的解,当函数图象与x 轴有两个交点,且交点的横坐标不是整数时,可通过不断缩小解所在的范围估计一元二次方程的解.
(3)交点横坐标即为一元二次方程ax2+bx+c=0 的解.
知2-讲
方法点拨:
估计一元二次方程的解的方法:
在难以读出公共点的坐标时,我们可以通过不断缩小解所在范围估计一元二次方程的解,对于y=ax2+bx+c(a≠0),如果ax21+bx1+c>0, 且ax22+bx2+c<0, 那么在x1与x2之间存在一个解, 取x3= ,若ax23+bx3+c>0, 则取x4= ; 若ax23+bx3+c<0,则取x4= .这样不停地取下去,直到达到所要求的精确度为止.
知2-讲
2. 利用二次函数y=ax2 的图象与直线y=-bx-c 的公共点求方程ax2+bx+c=0 的解
(1)将一元二次方程ax2+bx+c=0 化为ax2=-bx-c 的形式;
(2)在平面直角坐标系中画出抛物线y=ax2 和直线y=-bx-c,并确定抛物线与直线的公共点的坐标;
(3)公共点的横坐标即为一元二次方程ax2+bx+c=0 的解.
知2-讲
例2
利用二次函数的图象求一元二次方程-x2+2x-3=-8 的近似解(结果精确到0.1).
解题秘方一:画出二次函数y=-x2+2x+5 的图象,利用二次函数的图象与x轴的公共点计算方程的近似解.
知2-讲
特别提醒:
用图象法解一元二次方程是数形结合思想的具体应用,通过画函数的图象解一元二次方程是数的直观化的体现,但由于作图或观察存在误差,因此通过这种方法求得的方程的解一般是近似的.
知2-讲
解法一:整理方程,得-x2+2x+5=0.
作函数y=-x2+2x+5 的图象如图1.4-1.
由图象可知,抛物线与x 轴公共点的横坐标分别在-2 和-1,3 和4 之间,即方程-x2+2x-3=-8 的两个实数解分别在-2 和-1,3 和4 之间,用取平均数的方法不断缩小解的取值范围,从而确定方程的近似解.
知2-讲
知2-讲
由图象可知,当x=3 时,y>0;当x=4 时,y<0,
取3 和4 的平均数3.5,当x=3.5 时,y=-0.25,与x=3 时的函数值异号,所以方程的这个解在3 和3.5 之间.
取3 和3.5 的平均数3.25,当x=3.25 时,y=0.937 5,与x=3.5 时的函数值异号,所以方程的这个解在3.25 和3.5 之间.
知2-讲
取3.25 和3.5 的平均数3.375,当x=3.375 时,y=0.359 375,与x=3.5时的函数值异号,所以方程的这个解在3.375 和3.5 之间.
……
由此方法可得到原方程的一个近似解为3.4.
用同样的方法可得到原方程的另一个近似解为-1.4.
所以方程-x2+2x-3=-8 的解为x1≈ -1.4,x2≈ 3.4.
知2-讲
解题秘方二:画出二次函数y=-x2+2x-3 的图象,再画出直线y=-8,利用两图象的公共点求方程的近似解.
知2-讲
解法二:作出函数y=-x2+2x-3 的图象,
再画出直线y=-8,如图1.4-2.
由图象知,方程-x2+2x-3=-8 的解是抛物线
y=-x2+2x-3 与直线y=-8 的公共点的横坐标,一个公共点的横坐标在-2 与-1 之间,另一个公共点的横坐标在3 与4 之间.
同样用取平均数的方法,可得方程-x2+2x-3=-8 的解为x1 ≈ -1.4,x2 ≈ 3.4.
知2-讲
知2-讲
另解:
将原方程变形,得-x2=-2x-5, 画出函数y=-x2和y=-2x-5 的图象, 如图1.4-3.
由图可知,抛物线和直线交于A,B 两点,分别过A,B两点向x轴作垂线,可知A,B两点的横坐标分别约为-1.4和3.4,所以方程-x2+2x-3=-8的解是x1 ≈ -1.4,x2 ≈ 3.4.
知2-讲
知2-讲
解题通法:
用图象法求一元二次方程的近似解:
●先作出相应的二次函数的图象,确定一元二次方程的解的个数,找出公共点的横坐标的大致范围.
●然后利用取平均数的方法缩小解所在的范围,通过反复计算求出满足精确度要求的近似解.
知识点
二次函数y=ax2+bx+c的图象特征与a,b,c的符号关系(拓展点)
知3-讲
3
二次函数y=ax2+bx+c中,a 的符号决定抛物线的开口方向,ab的符号决定抛物线的对称轴的大致位置,c 的符号决定抛物线与y 轴交点的大致位置,b2-4ac 的符号决定抛物线与x轴的交点情况,具体如下表:
知3-讲
符号 图象的特征
a a>0 开口向上
a<0 开口向下
b=0 对称轴为y 轴
ab>0(a,b 同号) 对称轴在y 轴左侧
ab<0(a,b 异号) 对称轴在y 轴右侧
c c=0 图象过原点
c>0 图象与y 轴正半轴相交
c<0 图象与y 轴负半轴相交
b2-4ac b2-4ac=0 图象与x轴有唯一一个交点
b2-4ac>0 图象与x 轴有两个交点
b2-4ac<0 图象与x 轴没有交点
知3-讲
收藏夹:
对于二次函数y=ax2+bx+c:
当x=1 时,y=a+b+c,此时,若y=0,则a+b+c=0;
若y > 0,则a+b+c > 0;
若y < 0,则a+b+c < 0.
当x=-1 时,y=a-b+c,此时,若y=0,则a-b+c=0;
若y > 0,则a-b+c > 0;
若y < 0,则a-b+c < 0.
知3-讲
例 3
已知二次函数y=ax2+bx+c 的图象如图1.4-4,有下列结论:
① a+b+c<0;② a-b+c>0;③ abc>0;④ b2<4ac;⑤ b=2a. 其中正确的结论有( )
A. 4 个
B. 3 个
C. 2 个
D. 1 个
B
知3-讲
解:当x=1 时,对应的函数值y<0,即a+b+c<0,故①正确;
详解:
当x=1时,对应的函数值y=ax2+bx+c=a+b+c,观察图象可知此时抛物线上对应的点在x轴下方,说明此时的函数值y<0,即a+b+c<0.
知3-讲
当x=-1 时,对应的函数值y>0,即a-b+c>0,故②正确;观察图象知抛物线过原点,∴ c=0,∴ abc=0,故③错误;
∵抛物线与x轴有两个交点,∴ b2-4ac>0,即b2 > 4ac, 故④错误;
∵此抛物线的对称轴是直线x=-1,∴ - =-1,
∴ b=2a,故⑤正确.
知3-讲
解题秘方:根据二次函数的图象特征与a,b,c 之间的关系判断.
知3-讲
特别提醒:
抛物线y=ax2+bx+c的对称轴是直线x=- ,判断a,b之间的关系时,往往需要根据抛物线的对称轴的位置来判断.
二次函数与一元二次方程的联系
