湘教版九年级数学下册 1.5二次函数的应用课件(共22张PPT)
文档属性
| 名称 | 湘教版九年级数学下册 1.5二次函数的应用课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
1.5 二次函数的应用
第1章 二次函数
知识点
用二次函数解实际问题
知1-讲
1. 常用方法:利用二次函数解决实际问题,首先要建立数学模型,把实际问题转化为二次函数问题,利用题中存在的等量关系,求出函数表达式,然后利用函数的图象和性质去解决问题.
知1-讲
2. 一般步骤
(1)审:仔细审题,理清题意;
(2)找:找出问题中的变量和常量,分析它们之间的关系,与图形相关的问题要结合图形具体分析;
(3)列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,把实际问题转化成数学问题,根据题中的数量关系列出二次函数的表达式;
知1-讲
(4)解:依据已知条件,借助二次函数的表达式、图象和性质等求解实际问题;
(5)检:检验结果,得出符合实际意义的结论.
知1-讲
要点解读:
1. 用二次函数解实际问题时,审题是关键,检验容易被忽略,求得的结果除了要满足题中的数量关系,还要符合实际问题的意义.
2. 在实际问题中求最值时,解题思路是列二次函数表达式,用配方法把函数表达式化为y=a(x-h)2+k的形式求函数的最值,或者针对函数表达式用顶点坐标公式求函数的最值.
知1-讲
例 1
[中考·连云港] 如图1.5-1,利用一个直角墙角修建一个梯形储料场ABCD,其中∠ C=120°.若新建墙BC 与CD 总长为12 m,求该梯形储料场ABCD 的最大面积.
知1-讲
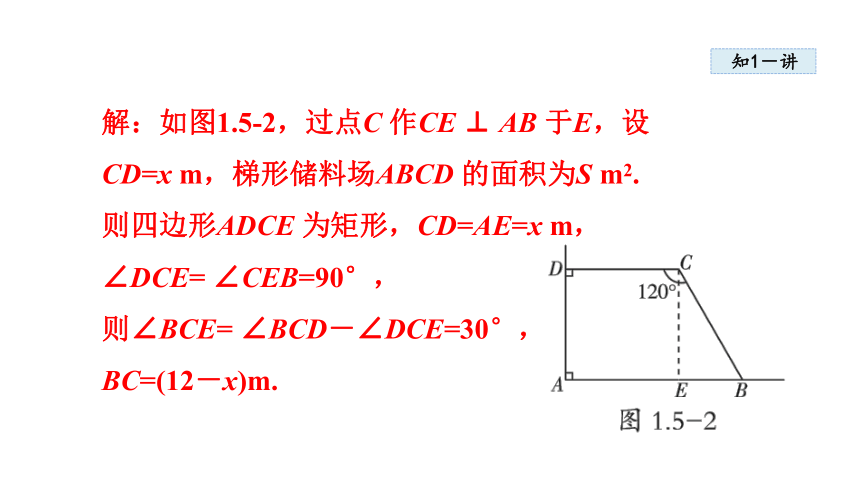
解:如图1.5-2,过点C 作CE ⊥ AB 于E,设
CD=x m,梯形储料场ABCD 的面积为S m2.
则四边形ADCE 为矩形,CD=AE=x m,
∠DCE= ∠CEB=90°,
则∠BCE= ∠BCD-∠DCE=30°,
BC=(12-x)m.
知1-讲
知1-讲
解题秘方:紧扣求图形面积的方法建立二次函数关系,利用二次函数的性质解决面积最值问题.
知1-讲
方法点拨:
几何图形中求最值,常用的建立函数关系的方法:
几何图形中的最值问题,一般都是利用二次函数的最值求解,根据几何图形建立二次函数的表达式就是解题的关键.
知1-讲
方法点拨:
一般在几何图形中建立函数关系有如下常用方法:
1.面积法:利用几何图形面积公式建立函数关系.
2.勾股法:利用勾股定理建立函数关系.
3.和差法:利用图形面积的和或差表示图形的面积,从而建立函数关系.
知1-讲
例2
某公司生产A型活动板房成本是每个425 元.图1.5-3 ①表示A型活动板房的一面墙,它由矩形和抛物线构成,矩形的长AD=4 m,宽AB=3 m,抛物线的最高点E到BC的
距离为4 m.
知1-讲
(1)按如图1.5-3①所示的直角坐标系,抛物线可以用y=kx2+m(k≠0)表示,求该抛物线的表达式;
解题秘方:根据图形及直角坐标系可得到D,E的坐标,代入y=kx2+m(k≠0)即可求解;
知1-讲
解:由题可知D(2,0),E(0,1),
易得 , 解得,
∴抛物线的表达式为y=- x2+1.
知1-讲
(2)现将A型活动板房改造为B型活动板房.如图1.5-3 ②,在抛物线与AD之间的区域内加装一扇矩形窗户FGMN,点G,M 在AD上,点N,F在抛物线上,窗户的
成本为50 元/m2.已知GM=2 m,求每
个B型活动板房的成本是多少.(每个B型
活动板房的成本= 每个A型活动板房的
成本+ 一扇窗户FGMN 的成本)
知1-讲
解题秘方:根据N 点与M点的横坐标相同,求出N点坐标,再求出矩形FGMN的面积,即可求解;
知1-讲
解:由题意可知N点与M点的横坐标相同.
∵GM=2 m,∴ OM=OG=1 m.
把x=1 代入y=- x2+1 中,得y= 3. ∴ N(1, )
∴ MN= m,
∴ S 矩形FGMN=GM×MN=2× = (m2),则一扇窗户的价格为 ×50=75(元). 因此每个B 型活动板房的成本为425+75=500(元).
知1-讲
(3)根据市场调查,以单价650 元销售(2)中的B型活动板房,每月能售出100 个,而单价每降低10 元,每月能多售出20 个.公司每月最多能生产160 个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
知1-讲
解题秘方:根据题意得到w关于n的二次函数,根据二次函数的性质即可求解.
知1-讲
解:根据题意可得w=(n-500)(100+20× )
=-2(n-600)2+20 000. ∵每月最多能生产160 个B 型活动板房,∴ 100+20× ≤160,解得n ≥ 620. ∵ -2 < 0,∴当n ≥ 620 时,w 随n 的增大而减小.
∴当n=620 时,w最大=19 200.
所以公司将销售单价定为620 元时,每月销售B 型活动板房所获利润最大,最大利润是19 200 元.
知1-讲
方法点拨:
利用二次函数解决利润最大问题的一般策略:
1. 明确利润、单价、销售量之间的关系,根据题意列出二次函数的表达式.
2. 讨论最大值时可借助顶点式y=a(x-h)2+k, 然后利用二次函数的性质确定最大值.
3. 在求商品利润最大的问题时,要注意实际问题中自变量的取值范围,有时根据顶点坐标求出的最大值并不一定是函数在实际问题中的最大值,实际问题的最大值应在自变量的取值范围内取得.
二次函数的应用
图形面积
实际问题
分类
数学
模型
利润问题
增减性
最值
转化
二次函数
抛物线形
1.5 二次函数的应用
第1章 二次函数
知识点
用二次函数解实际问题
知1-讲
1. 常用方法:利用二次函数解决实际问题,首先要建立数学模型,把实际问题转化为二次函数问题,利用题中存在的等量关系,求出函数表达式,然后利用函数的图象和性质去解决问题.
知1-讲
2. 一般步骤
(1)审:仔细审题,理清题意;
(2)找:找出问题中的变量和常量,分析它们之间的关系,与图形相关的问题要结合图形具体分析;
(3)列:用二次函数表示出变量和常量之间的关系,建立二次函数模型,把实际问题转化成数学问题,根据题中的数量关系列出二次函数的表达式;
知1-讲
(4)解:依据已知条件,借助二次函数的表达式、图象和性质等求解实际问题;
(5)检:检验结果,得出符合实际意义的结论.
知1-讲
要点解读:
1. 用二次函数解实际问题时,审题是关键,检验容易被忽略,求得的结果除了要满足题中的数量关系,还要符合实际问题的意义.
2. 在实际问题中求最值时,解题思路是列二次函数表达式,用配方法把函数表达式化为y=a(x-h)2+k的形式求函数的最值,或者针对函数表达式用顶点坐标公式求函数的最值.
知1-讲
例 1
[中考·连云港] 如图1.5-1,利用一个直角墙角修建一个梯形储料场ABCD,其中∠ C=120°.若新建墙BC 与CD 总长为12 m,求该梯形储料场ABCD 的最大面积.
知1-讲
解:如图1.5-2,过点C 作CE ⊥ AB 于E,设
CD=x m,梯形储料场ABCD 的面积为S m2.
则四边形ADCE 为矩形,CD=AE=x m,
∠DCE= ∠CEB=90°,
则∠BCE= ∠BCD-∠DCE=30°,
BC=(12-x)m.
知1-讲
知1-讲
解题秘方:紧扣求图形面积的方法建立二次函数关系,利用二次函数的性质解决面积最值问题.
知1-讲
方法点拨:
几何图形中求最值,常用的建立函数关系的方法:
几何图形中的最值问题,一般都是利用二次函数的最值求解,根据几何图形建立二次函数的表达式就是解题的关键.
知1-讲
方法点拨:
一般在几何图形中建立函数关系有如下常用方法:
1.面积法:利用几何图形面积公式建立函数关系.
2.勾股法:利用勾股定理建立函数关系.
3.和差法:利用图形面积的和或差表示图形的面积,从而建立函数关系.
知1-讲
例2
某公司生产A型活动板房成本是每个425 元.图1.5-3 ①表示A型活动板房的一面墙,它由矩形和抛物线构成,矩形的长AD=4 m,宽AB=3 m,抛物线的最高点E到BC的
距离为4 m.
知1-讲
(1)按如图1.5-3①所示的直角坐标系,抛物线可以用y=kx2+m(k≠0)表示,求该抛物线的表达式;
解题秘方:根据图形及直角坐标系可得到D,E的坐标,代入y=kx2+m(k≠0)即可求解;
知1-讲
解:由题可知D(2,0),E(0,1),
易得 , 解得,
∴抛物线的表达式为y=- x2+1.
知1-讲
(2)现将A型活动板房改造为B型活动板房.如图1.5-3 ②,在抛物线与AD之间的区域内加装一扇矩形窗户FGMN,点G,M 在AD上,点N,F在抛物线上,窗户的
成本为50 元/m2.已知GM=2 m,求每
个B型活动板房的成本是多少.(每个B型
活动板房的成本= 每个A型活动板房的
成本+ 一扇窗户FGMN 的成本)
知1-讲
解题秘方:根据N 点与M点的横坐标相同,求出N点坐标,再求出矩形FGMN的面积,即可求解;
知1-讲
解:由题意可知N点与M点的横坐标相同.
∵GM=2 m,∴ OM=OG=1 m.
把x=1 代入y=- x2+1 中,得y= 3. ∴ N(1, )
∴ MN= m,
∴ S 矩形FGMN=GM×MN=2× = (m2),则一扇窗户的价格为 ×50=75(元). 因此每个B 型活动板房的成本为425+75=500(元).
知1-讲
(3)根据市场调查,以单价650 元销售(2)中的B型活动板房,每月能售出100 个,而单价每降低10 元,每月能多售出20 个.公司每月最多能生产160 个B型活动板房.不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?
知1-讲
解题秘方:根据题意得到w关于n的二次函数,根据二次函数的性质即可求解.
知1-讲
解:根据题意可得w=(n-500)(100+20× )
=-2(n-600)2+20 000. ∵每月最多能生产160 个B 型活动板房,∴ 100+20× ≤160,解得n ≥ 620. ∵ -2 < 0,∴当n ≥ 620 时,w 随n 的增大而减小.
∴当n=620 时,w最大=19 200.
所以公司将销售单价定为620 元时,每月销售B 型活动板房所获利润最大,最大利润是19 200 元.
知1-讲
方法点拨:
利用二次函数解决利润最大问题的一般策略:
1. 明确利润、单价、销售量之间的关系,根据题意列出二次函数的表达式.
2. 讨论最大值时可借助顶点式y=a(x-h)2+k, 然后利用二次函数的性质确定最大值.
3. 在求商品利润最大的问题时,要注意实际问题中自变量的取值范围,有时根据顶点坐标求出的最大值并不一定是函数在实际问题中的最大值,实际问题的最大值应在自变量的取值范围内取得.
二次函数的应用
图形面积
实际问题
分类
数学
模型
利润问题
增减性
最值
转化
二次函数
抛物线形
