湘教版九年级数学下册 1.1二次函数课件(共19张PPT)
文档属性
| 名称 | 湘教版九年级数学下册 1.1二次函数课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
1.1 二次函数
第1章 二次函数
知识点
二次函数的定义
知1-讲
1
1. 定义:如果函数的表达式是自变量的二次多项式,那么,这样的函数称为二次函数,它的一般形式是y=ax2+bx+c(a,b,c 是常数,a ≠ 0). 其中x 是自变量,a,b,c 分别是函数表达式的二次项系数、一次项系数和常数项.
知1-讲
详解:
二次函数的特殊形式:
●只含二次项,即:y=ax2(b=0,c=0);
●不含一次项,即:y = ax2 + c (b=0,c≠ 0);
●不含常数项,即:y=ax2+bx(b≠0,c=0).
知1-讲
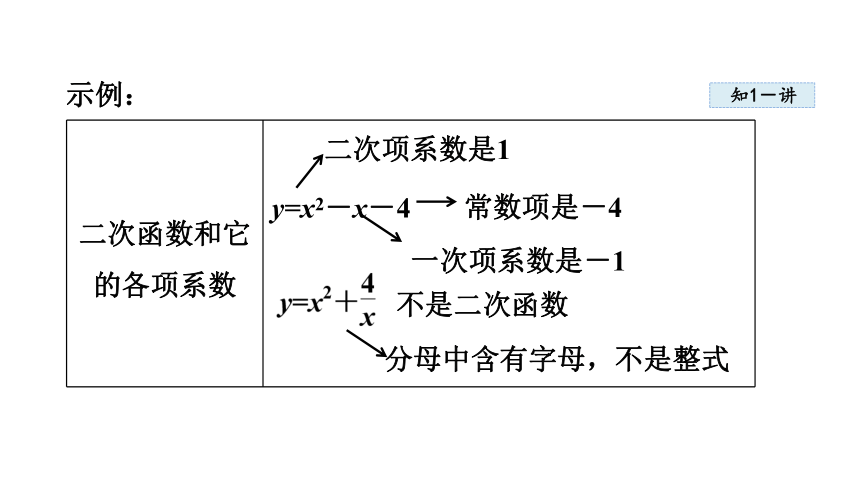
示例:
二次函数和它的各项系数
y=x2-x-4
二次项系数是1
常数项是-4
一次项系数是-1
不是二次函数
分母中含有字母,不是整式
知1-讲
2. 确定二次函数的“三要素”
(1)含有自变量的代数式必须是整式;
(2)化简后自变量的最高次数是2;
(3)二次项系数不等于0.
“三要素”要牢记,这是确定二次函数的关键.
知1-讲
例 1
当m 取何值时,函数y=(m2+m)xm2-2m-1+(m-5)+m2是关于x 的二次函数?并求出这时二次函数的表达式.
解:由题意,得
∴ m=3.
∴当m=3 时,该函数是关于x 的二次函数,
表达式为:y=(32+3)x32-2×3-1+(3-5)x+32,
即y=12x2-2x+9.
知1-讲
解题秘方:紧扣二次函数定义的“三要素”进行解答.
特别警示:
当函数的二次项系数包含字母时,要注意二次项系数不为0,解此类题时易只关注满足指数的要求,而忽略对二次项系数的限制,从而导致错误.
知2-讲
知识点
建立二次函数模型表示变量间的关系
2
建立二次函数模型的一般步骤
(1)审清题意:找出问题中的已知量(常量)和未知量(变量),把问题中的文字或图形语言转化成数学语言.
(2)找相等关系:分析常量和变量之间的关系,列出等式.
知2-讲
(3)列二次函数表达式:设出表示变量的字母,把相等关系用含字母的式子表示并把它整理成二次函数的一般形式.
(4)确定函数自变量的取值范围:二次函数的自变量在一般情况下是没有条件限制的,即自变量可以取一切实数,但是在实际问题中,变量都有一定的实际意义,要受到一定的条件限制,所以在求出二次函数的表达式后,还要指明自变量的取值范围.
知2-讲
特别提醒:
1. 建立二次函数模型与建立一元二次方程模型类似,不同的是需将它转化为用含一个未知数(自变量)的代数式表示另一个未知数(函数).
2. 自变量的取值范围应使实际问题有意义.
知2-讲
例2
某网店销售某款童装,每件售价60 元,每星期可卖300 件. 为了促销,该网店决定降价销售. 市场调查反映,每降价1 元,每星期可多卖30 件. 已知该款童装每件的成本价为40 元,设该款童装每件的售价 为x 元,每星期的销售量为y 件.
知2-讲
(1)求y与x 之间的函数表达式,并写出自变量的取值范围;
(2)设每星期的销售利润为W 元,求W 与x 之间的函数表达式.
解: y=300+30(60-x)=-30x+2 100(40 ≤ x ≤ 60).
W=(x-40)(-30x+2 100)=-30x2+3 300x-84 000.
知2-讲
方法点拨:在实际问题中建立二次函数模型时,关键要找出两个变量之间的数量关系,用类似建立一元二次方程模型的方法,借助方程思想求出二次函数的表达式.
知2-讲
详解:
相等关系:
●降价后的销售量=降价前可卖件数+降价后多卖的件数,每件降价(60-x)元;
●销售利润=每件的利润×销售量,每件的利润为(x-40)元.
知1-讲
例 3
某校为绿化校园,在一块长为15 m、宽为10 m 的矩形空地上建造一个矩形花圃, 如图1.1-1,设计这个花圃的一边靠墙(墙长大于15 m), 并在不靠墙的三边各留出一条宽相等的小路,设小路的宽为x m,花圃的面积为y m2,求y关于x 的函数表达式,并写出
函数自变量的取值范围.
知1-讲
解:由小路的宽为x m,知矩形花圃的长为(15-2x)m,宽为(10-x)m. 根据题意,得y=(15-2x)(10-x)=2x2-35x+150.
由 x > 0,
15-2x>0,解得0 < x < 7.5.
10-x > 0,
故所求的函数表达式为y=2x2-35x+150(0<x< 7.5).
知1-讲
解题秘方:紧扣矩形花圃的面积公式建立二次函数表达式,关键是利用宽度确定自变量的取值范围.
知1-讲
特别提醒:
实际问题中自变量的取值范围的确定:
1. 二次函数自变量的取值范围一般是全体实数,但是在实际问题中,自变量的取值范围有时会有一定的限制,自变量所取的值应使实际问题有意义.
2. 确定自变量的取值范围时,需根据题意正确列出不等式或不等式组,通过解不等式或不等式组得出实际问题中自变量的取值范围.
二次函数
二次函数
定义
表达式
三要素
自变量的
取值范围
y=ax2
y=ax2+c
y=ax2+bx
y=ax2+bx+c
1.1 二次函数
第1章 二次函数
知识点
二次函数的定义
知1-讲
1
1. 定义:如果函数的表达式是自变量的二次多项式,那么,这样的函数称为二次函数,它的一般形式是y=ax2+bx+c(a,b,c 是常数,a ≠ 0). 其中x 是自变量,a,b,c 分别是函数表达式的二次项系数、一次项系数和常数项.
知1-讲
详解:
二次函数的特殊形式:
●只含二次项,即:y=ax2(b=0,c=0);
●不含一次项,即:y = ax2 + c (b=0,c≠ 0);
●不含常数项,即:y=ax2+bx(b≠0,c=0).
知1-讲
示例:
二次函数和它的各项系数
y=x2-x-4
二次项系数是1
常数项是-4
一次项系数是-1
不是二次函数
分母中含有字母,不是整式
知1-讲
2. 确定二次函数的“三要素”
(1)含有自变量的代数式必须是整式;
(2)化简后自变量的最高次数是2;
(3)二次项系数不等于0.
“三要素”要牢记,这是确定二次函数的关键.
知1-讲
例 1
当m 取何值时,函数y=(m2+m)xm2-2m-1+(m-5)+m2是关于x 的二次函数?并求出这时二次函数的表达式.
解:由题意,得
∴ m=3.
∴当m=3 时,该函数是关于x 的二次函数,
表达式为:y=(32+3)x32-2×3-1+(3-5)x+32,
即y=12x2-2x+9.
知1-讲
解题秘方:紧扣二次函数定义的“三要素”进行解答.
特别警示:
当函数的二次项系数包含字母时,要注意二次项系数不为0,解此类题时易只关注满足指数的要求,而忽略对二次项系数的限制,从而导致错误.
知2-讲
知识点
建立二次函数模型表示变量间的关系
2
建立二次函数模型的一般步骤
(1)审清题意:找出问题中的已知量(常量)和未知量(变量),把问题中的文字或图形语言转化成数学语言.
(2)找相等关系:分析常量和变量之间的关系,列出等式.
知2-讲
(3)列二次函数表达式:设出表示变量的字母,把相等关系用含字母的式子表示并把它整理成二次函数的一般形式.
(4)确定函数自变量的取值范围:二次函数的自变量在一般情况下是没有条件限制的,即自变量可以取一切实数,但是在实际问题中,变量都有一定的实际意义,要受到一定的条件限制,所以在求出二次函数的表达式后,还要指明自变量的取值范围.
知2-讲
特别提醒:
1. 建立二次函数模型与建立一元二次方程模型类似,不同的是需将它转化为用含一个未知数(自变量)的代数式表示另一个未知数(函数).
2. 自变量的取值范围应使实际问题有意义.
知2-讲
例2
某网店销售某款童装,每件售价60 元,每星期可卖300 件. 为了促销,该网店决定降价销售. 市场调查反映,每降价1 元,每星期可多卖30 件. 已知该款童装每件的成本价为40 元,设该款童装每件的售价 为x 元,每星期的销售量为y 件.
知2-讲
(1)求y与x 之间的函数表达式,并写出自变量的取值范围;
(2)设每星期的销售利润为W 元,求W 与x 之间的函数表达式.
解: y=300+30(60-x)=-30x+2 100(40 ≤ x ≤ 60).
W=(x-40)(-30x+2 100)=-30x2+3 300x-84 000.
知2-讲
方法点拨:在实际问题中建立二次函数模型时,关键要找出两个变量之间的数量关系,用类似建立一元二次方程模型的方法,借助方程思想求出二次函数的表达式.
知2-讲
详解:
相等关系:
●降价后的销售量=降价前可卖件数+降价后多卖的件数,每件降价(60-x)元;
●销售利润=每件的利润×销售量,每件的利润为(x-40)元.
知1-讲
例 3
某校为绿化校园,在一块长为15 m、宽为10 m 的矩形空地上建造一个矩形花圃, 如图1.1-1,设计这个花圃的一边靠墙(墙长大于15 m), 并在不靠墙的三边各留出一条宽相等的小路,设小路的宽为x m,花圃的面积为y m2,求y关于x 的函数表达式,并写出
函数自变量的取值范围.
知1-讲
解:由小路的宽为x m,知矩形花圃的长为(15-2x)m,宽为(10-x)m. 根据题意,得y=(15-2x)(10-x)=2x2-35x+150.
由 x > 0,
15-2x>0,解得0 < x < 7.5.
10-x > 0,
故所求的函数表达式为y=2x2-35x+150(0<x< 7.5).
知1-讲
解题秘方:紧扣矩形花圃的面积公式建立二次函数表达式,关键是利用宽度确定自变量的取值范围.
知1-讲
特别提醒:
实际问题中自变量的取值范围的确定:
1. 二次函数自变量的取值范围一般是全体实数,但是在实际问题中,自变量的取值范围有时会有一定的限制,自变量所取的值应使实际问题有意义.
2. 确定自变量的取值范围时,需根据题意正确列出不等式或不等式组,通过解不等式或不等式组得出实际问题中自变量的取值范围.
二次函数
二次函数
定义
表达式
三要素
自变量的
取值范围
y=ax2
y=ax2+c
y=ax2+bx
y=ax2+bx+c
