湘教版九年级数学下册 3.2直棱柱、圆锥的侧面展开图课件(共25张PPT)
文档属性
| 名称 | 湘教版九年级数学下册 3.2直棱柱、圆锥的侧面展开图课件(共25张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
3.2 直棱柱、圆锥的侧面展开图
第3章 投影与视图
知识点
直棱柱
知1-讲
1
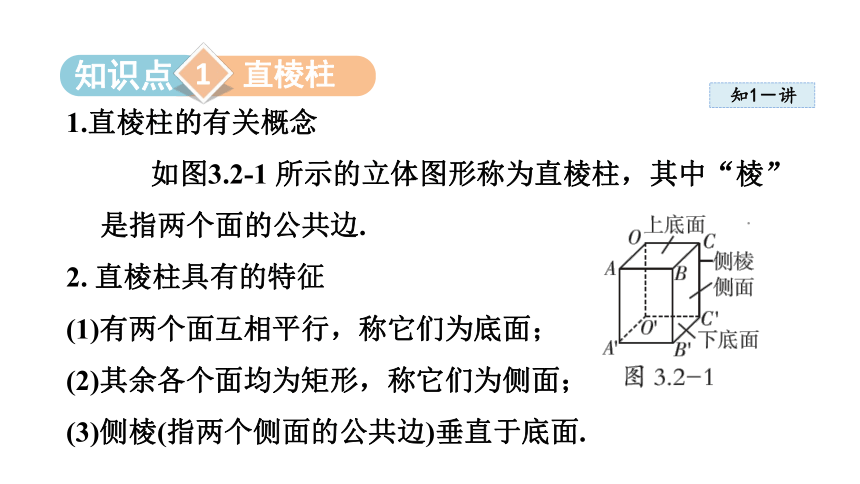
1.直棱柱的有关概念
如图3.2-1 所示的立体图形称为直棱柱,其中“棱”是指两个面的公共边.
2. 直棱柱具有的特征
(1)有两个面互相平行,称它们为底面;
(2)其余各个面均为矩形,称它们为侧面;
(3)侧棱(指两个侧面的公共边)垂直于底面.
知1-讲
3. 直棱柱的命名
根据底面图形的边数,将直棱柱分别称为直三棱柱、直四棱柱、直五棱柱、直六棱柱等. 例如,长方体和正方体都是直四棱柱.
4. 正棱柱
底面是正多边形的直棱柱叫作正棱柱.
知1-讲
特别提醒:
●直棱柱的两个底面是全等的多边形.
●直棱柱的侧面都是矩形,侧棱互相平行且相等.
●直棱柱的侧棱必须与底面垂直,侧棱与底面不垂直的棱柱不是直棱柱.
●直棱柱的侧棱数,侧面数都等于底面的边数.
知1-讲
例 1
在如图3.2-2 所示的直六棱柱中,侧棱长为6 cm,底面边长都是3 cm.
知1-讲
解题秘方:紧扣直棱柱的特点,认清直棱柱各部分的名称是解题关键.
方法点拨:
直棱柱的底面是两个全等的多边形,多边形的边有几条,就是直几棱柱,而且直棱柱的侧面都是矩形.
知1-讲
(1)一共有多少条棱?长度分别是多少?
解:一共有18 条棱,其中有6 条侧棱,其长度都为6 cm,其余的棱都等于底面边长,其长度都为3 cm.
知1-讲
(2)一共有多少个面?它们分别是什么形状?哪些面的形状一定相同?
解:一共有8个面,其中2个底面都为六边形,这2个底面的形状完全相同,6个侧面都为矩形,这6个侧面的形状完全相同.
知2-讲
知识点
直棱柱的侧面展开图
2
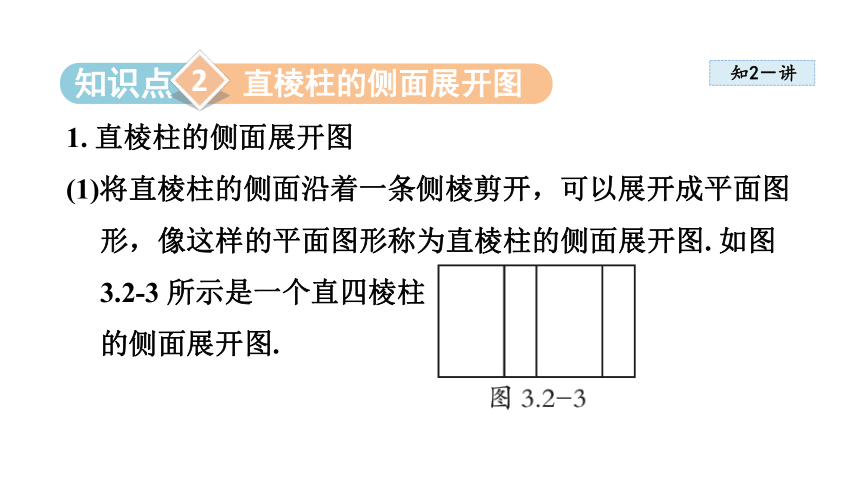
1. 直棱柱的侧面展开图
(1)将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形,像这样的平面图形称为直棱柱的侧面展开图. 如图3.2-3 所示是一个直四棱柱
的侧面展开图.
知2-讲
(2)直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高).
2. 直棱柱的侧面积
直棱柱的侧面积可以利用其侧面展开图是矩形来求,即直棱柱的侧面积=直棱柱的底面周长× 侧棱长(高).
知2-讲
特别提醒:
沿直棱柱表面不同的棱剪开,可得到不同组合方式的表面展开图,以直三棱柱为例,如图3.2-4 所示,①②③依次为沿不同的棱剪开而得到的直三棱柱表面展开图.
知2-讲
如图3.2-5, 矩形ABCD 是一个直四棱柱的底面, 其中AB=3,AC=5,这个直四棱柱的侧棱长为8,求它的侧面积.
解题秘方:利用直棱柱的侧面积= 直棱柱的底面周长× 侧棱长求侧面积是解题的关键.
例2
知2-讲
解:根据勾股定理,得BC= =4.
∴这个直四棱柱的底面周长l=2(AB+BC)=2×(3+4)=14,
∴ S侧=14×8=112.
故这个直四棱柱的侧面积是112.
知识点
圆锥
知3-讲
3
1. 与圆锥有关的概念
(1)圆锥:如图3.2-6 所示的立体图形称为圆锥,圆锥是由一个底面和一个侧面围成的图形. 圆锥
可以看作一个直角三角形绕它的一条
直角边所在的直线旋转一周所形成的
图形. 这条直线叫作圆锥的轴.
知3-讲
特别提醒:
1. 圆锥的轴通过底面的圆心,并且垂直于底面;
2. 圆锥的母线长都相等;
3. 圆锥的母线l、高h 及底面圆的半径r 构成直角三角形,有l2=h2+r2,已知l,h 和r 中任意两个量都可以求出第三个量.
知3-讲
(2)圆锥的高:圆锥的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高.
(3)圆锥的母线:圆锥顶点与底面圆上任意一点的连线段都叫作圆锥的母线.
知3-讲
2. 圆锥的侧面积和表面积
如图3.2-7,把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,像这样的平面图形称为圆锥的侧面展开图. 圆锥的侧面展开图是一个扇形.
警示误区:
解决有关圆锥的计算题的关键是理清立体图形与表面展开图的联系与区别,特别是不要混淆底面圆半径r和侧面展开图(扇形)的半径l. 记住:圆锥侧面展开图(扇形)的半径为圆锥的母线长.
知3-讲
设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr, 因此S 侧=S 扇形=
×2πr×l=πrl,S 表=S 侧+S 底=πrl+πr2=πr(l+r).
知3-讲
如图3.2 -8,在△ ABC 中,∠ C= 90°,AC=3,BC=4.
例 3
知3-讲
(1)将△ ABC 以BC 所在直线为轴旋转一周,求所得旋转体的表面积;
解题秘方:所得旋转体是一个圆锥,其表面积等于侧面展开图(扇形)的面积与底面圆的面积之和.
知3-讲
解:∵∠ C=90°,AC=3,BC=4,
∴ AB= =5.
∴ S底=πAC2=9π,S侧=π×3×5=15π.
∴ S表=S底+S侧=24π.
知3-讲
(2)将△ ABC 以AC 所在直线为轴旋转一周,求所得旋转体的表面积.
解题秘方:所得旋转体是一个圆锥,其表面积等于侧面展开图(扇形)的面积与底面圆的面积之和.
知3-讲
解:∵ S底=πBC2=16π,S侧=π×4×5=20π,
∴ S表=S底+S侧=36π.
知3-讲
特别提醒:
关于圆锥的计算的题型主要有三种形式:
1. 已知圆锥的底面圆半径、高、母线长中任意的两个量,求圆锥的侧面积或表面积;
2. 知道圆锥的侧面积和底面圆半径,求母线长或高或圆锥侧面展开图的圆心角度数;
3. 已知圆锥侧面展开图的弧长及圆心角度数,求圆锥的底面圆半径或高.
直棱柱、圆锥的侧面展开图
立体图形
侧面
平面图形
直棱柱
体积与表面积
展开图
圆锥
3.2 直棱柱、圆锥的侧面展开图
第3章 投影与视图
知识点
直棱柱
知1-讲
1
1.直棱柱的有关概念
如图3.2-1 所示的立体图形称为直棱柱,其中“棱”是指两个面的公共边.
2. 直棱柱具有的特征
(1)有两个面互相平行,称它们为底面;
(2)其余各个面均为矩形,称它们为侧面;
(3)侧棱(指两个侧面的公共边)垂直于底面.
知1-讲
3. 直棱柱的命名
根据底面图形的边数,将直棱柱分别称为直三棱柱、直四棱柱、直五棱柱、直六棱柱等. 例如,长方体和正方体都是直四棱柱.
4. 正棱柱
底面是正多边形的直棱柱叫作正棱柱.
知1-讲
特别提醒:
●直棱柱的两个底面是全等的多边形.
●直棱柱的侧面都是矩形,侧棱互相平行且相等.
●直棱柱的侧棱必须与底面垂直,侧棱与底面不垂直的棱柱不是直棱柱.
●直棱柱的侧棱数,侧面数都等于底面的边数.
知1-讲
例 1
在如图3.2-2 所示的直六棱柱中,侧棱长为6 cm,底面边长都是3 cm.
知1-讲
解题秘方:紧扣直棱柱的特点,认清直棱柱各部分的名称是解题关键.
方法点拨:
直棱柱的底面是两个全等的多边形,多边形的边有几条,就是直几棱柱,而且直棱柱的侧面都是矩形.
知1-讲
(1)一共有多少条棱?长度分别是多少?
解:一共有18 条棱,其中有6 条侧棱,其长度都为6 cm,其余的棱都等于底面边长,其长度都为3 cm.
知1-讲
(2)一共有多少个面?它们分别是什么形状?哪些面的形状一定相同?
解:一共有8个面,其中2个底面都为六边形,这2个底面的形状完全相同,6个侧面都为矩形,这6个侧面的形状完全相同.
知2-讲
知识点
直棱柱的侧面展开图
2
1. 直棱柱的侧面展开图
(1)将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形,像这样的平面图形称为直棱柱的侧面展开图. 如图3.2-3 所示是一个直四棱柱
的侧面展开图.
知2-讲
(2)直棱柱的侧面展开图是一个矩形,这个矩形的长是直棱柱的底面周长,宽是直棱柱的侧棱长(高).
2. 直棱柱的侧面积
直棱柱的侧面积可以利用其侧面展开图是矩形来求,即直棱柱的侧面积=直棱柱的底面周长× 侧棱长(高).
知2-讲
特别提醒:
沿直棱柱表面不同的棱剪开,可得到不同组合方式的表面展开图,以直三棱柱为例,如图3.2-4 所示,①②③依次为沿不同的棱剪开而得到的直三棱柱表面展开图.
知2-讲
如图3.2-5, 矩形ABCD 是一个直四棱柱的底面, 其中AB=3,AC=5,这个直四棱柱的侧棱长为8,求它的侧面积.
解题秘方:利用直棱柱的侧面积= 直棱柱的底面周长× 侧棱长求侧面积是解题的关键.
例2
知2-讲
解:根据勾股定理,得BC= =4.
∴这个直四棱柱的底面周长l=2(AB+BC)=2×(3+4)=14,
∴ S侧=14×8=112.
故这个直四棱柱的侧面积是112.
知识点
圆锥
知3-讲
3
1. 与圆锥有关的概念
(1)圆锥:如图3.2-6 所示的立体图形称为圆锥,圆锥是由一个底面和一个侧面围成的图形. 圆锥
可以看作一个直角三角形绕它的一条
直角边所在的直线旋转一周所形成的
图形. 这条直线叫作圆锥的轴.
知3-讲
特别提醒:
1. 圆锥的轴通过底面的圆心,并且垂直于底面;
2. 圆锥的母线长都相等;
3. 圆锥的母线l、高h 及底面圆的半径r 构成直角三角形,有l2=h2+r2,已知l,h 和r 中任意两个量都可以求出第三个量.
知3-讲
(2)圆锥的高:圆锥的底面是一个圆,连接顶点与底面圆心的线段叫作圆锥的高.
(3)圆锥的母线:圆锥顶点与底面圆上任意一点的连线段都叫作圆锥的母线.
知3-讲
2. 圆锥的侧面积和表面积
如图3.2-7,把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,像这样的平面图形称为圆锥的侧面展开图. 圆锥的侧面展开图是一个扇形.
警示误区:
解决有关圆锥的计算题的关键是理清立体图形与表面展开图的联系与区别,特别是不要混淆底面圆半径r和侧面展开图(扇形)的半径l. 记住:圆锥侧面展开图(扇形)的半径为圆锥的母线长.
知3-讲
设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr, 因此S 侧=S 扇形=
×2πr×l=πrl,S 表=S 侧+S 底=πrl+πr2=πr(l+r).
知3-讲
如图3.2 -8,在△ ABC 中,∠ C= 90°,AC=3,BC=4.
例 3
知3-讲
(1)将△ ABC 以BC 所在直线为轴旋转一周,求所得旋转体的表面积;
解题秘方:所得旋转体是一个圆锥,其表面积等于侧面展开图(扇形)的面积与底面圆的面积之和.
知3-讲
解:∵∠ C=90°,AC=3,BC=4,
∴ AB= =5.
∴ S底=πAC2=9π,S侧=π×3×5=15π.
∴ S表=S底+S侧=24π.
知3-讲
(2)将△ ABC 以AC 所在直线为轴旋转一周,求所得旋转体的表面积.
解题秘方:所得旋转体是一个圆锥,其表面积等于侧面展开图(扇形)的面积与底面圆的面积之和.
知3-讲
解:∵ S底=πBC2=16π,S侧=π×4×5=20π,
∴ S表=S底+S侧=36π.
知3-讲
特别提醒:
关于圆锥的计算的题型主要有三种形式:
1. 已知圆锥的底面圆半径、高、母线长中任意的两个量,求圆锥的侧面积或表面积;
2. 知道圆锥的侧面积和底面圆半径,求母线长或高或圆锥侧面展开图的圆心角度数;
3. 已知圆锥侧面展开图的弧长及圆心角度数,求圆锥的底面圆半径或高.
直棱柱、圆锥的侧面展开图
立体图形
侧面
平面图形
直棱柱
体积与表面积
展开图
圆锥
