湘教版九年级数学下册3.1投 影课件(共50张PPT)
文档属性
| 名称 | 湘教版九年级数学下册3.1投 影课件(共50张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 16:08:57 | ||
图片预览









文档简介
(共50张PPT)
3.1 投 影
第3章 投影与视图
知识点
投影
知1-讲
1
1. 定义 光线照射物体,会在平面上(如地面、墙壁)留下它的影子,把物体映成它的影子叫作投影. 照射的光线叫投影线,投影所在的平面叫投影面. 物体在投影下的像简称为物体的投影.
特别提醒:
形成投影应具备的条件:
●要有物体存在且物体处于光源与投影面之间;
●要有光线;
●要有一个呈现投影的面, 即投影面(投影面应是平的).
知1-讲
2. 性质
(1)光线是沿直线照射的,因此可以由物体与它的投影确定光线的方向.
(2)不同时刻,物体的影子的方向和大小会发生变化. 在相同的投影线和投影面的情况下,不同形状的物体的投影一般不同.
知1-讲
例 1
下列现象不属于投影的是( )
A. 皮影 B. 树影 C. 手影 D. 素描画
D
解题秘方:紧扣“投影的定义”中的三个条件进行识别.
知1-讲
特别提醒:
●投影是生活中一种常见的现象,没有特殊说明时,本章中的投影问题均指在平面上形成的投影.
●投影现象的特点:光线、物体、投影面的相对位置发生变化,物体的影子就会相应发变化.
知1-讲
解:皮影、树影和手影都符合“用光线照射物体在某个平面上得到的影子”,因此选项A,B,C 都属于投影. 用排除法选D.
知1-讲
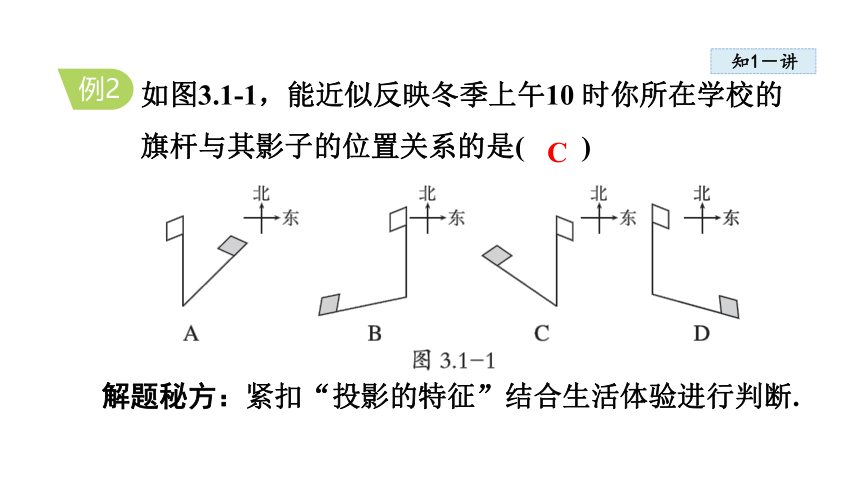
如图3.1-1,能近似反映冬季上午10 时你所在学校的旗杆与其影子的位置关系的是( )
例2
C
解题秘方:紧扣“投影的特征”结合生活体验进行判断.
知1-讲
解:冬季上午10 时太阳光下物体的影子应大致为西北方向.
知1-讲
知识储备:
1. 一天内旗杆影子的变化情况;
2. 物体上一点与它的投影的对应点的连线为投影线.
知2-讲
知识点
平行投影
2
1. 定义 由于太阳距离地球很远,从太阳射到地面的光线可以看成平行光线,因此这种投影称为平行投影.
注意:平行投影的投影线都是平行的.
知2-讲
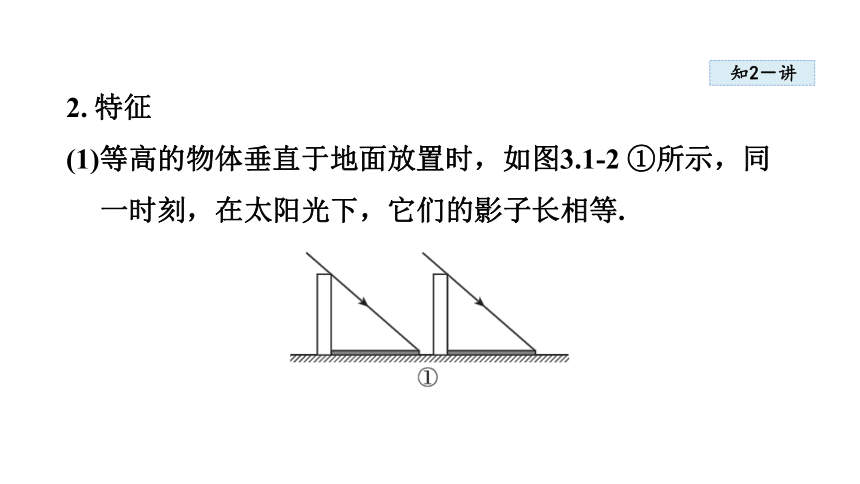
2. 特征
(1)等高的物体垂直于地面放置时,如图3.1-2 ①所示,同一时刻,在太阳光下,它们的影子长相等.
知2-讲
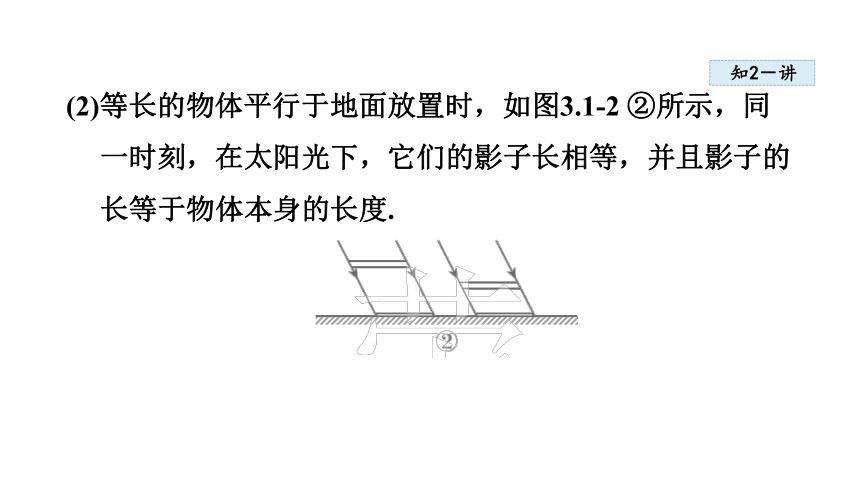
(2)等长的物体平行于地面放置时,如图3.1-2 ②所示,同一时刻,在太阳光下,它们的影子长相等,并且影子的长等于物体本身的长度.
知2-讲
(3)在太阳光下,不同时刻,同一地点、同一物体的影子不仅方向在改变,影子的长度一般也不同,从早晨到傍晚,物体影子的指向是正西→西北→正北→东北→正东(北半球北回归线以北地区). 一天之中,同一物体的影子的长短的变化规律是长→短→最短→短→长.
(4)在太阳光下,不同时刻,同一物体的影子长度不同;同一时刻,不同物体本身的高度与它们的影子长度成正比.
知2-讲
特别提醒:
这一结论可以用相似三角形的性质得到,即
知2-讲
小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的影子不可能是图3.1-3 中的( )
例 3
解题秘方:紧扣“在阳光下,平行且相等的边的平行投影是平行且相等的,也可能是互相重合的”这一特征解答.
A
知2-讲
解题通法:
平行投影中,不同位置、不同时刻,同一物体的影子的大小、形状可能不同,具体形状应视其外在形状及其与光线的夹角而定.平行且相等的边的投影也平行且相等,也可能互相重合.
知2-讲
解:矩形木框在地面上形成的影子应是平行四边形或是一条线段,故不会是梯形.
知2-讲
如图3.1-4,AB 和DE 是直立在地面上的两根立柱,AB=5 m,某一时刻AB 在阳光下的投影BC=3 m.
例4
知2-讲
解法提醒:
画物体的平行投影的方法:
先根据物体的投影确定光线,然后利用两个物体的顶端与各自影子的顶端的连线是一组平行线,过物体顶端作平行线与投影面相交,从而确定其影子.
知2-讲
(1)请你在图中画出此时DE 在阳光下的投影(用线段EF 表示);
解题秘方:紧扣“平行投影的特征”中投影线、影子、物高的特征解答.
知2-讲
解:如图3.1-5,连接AC,过点D 作DF ∥ AC,交直线BE 于点F,则EF 就是DE 的投影.
知2-讲
(2)在测量AB 的投影时,同时测量出DE 在阳光下的投影EF=6 m,请你计算DE 的长.
解题秘方:紧扣“平行投影的特征”中投影线、影子、物高的特征解答.
知2-讲
解:∵在阳光下,同一时刻物高与影长的比相等,∴
∵ AB=5 m,BC=3 m,EF=6 m,
∴ DE= =10m.
知识点
中心投影
知3-讲
3
1. 定义 如果光线从一点发出(如灯泡、电影放映机、幻灯机的光线),这样的投影称为中心投影.
特别提醒:中心投影的光源是点光源,它的光线相交于一点,常见的点光源有手电筒、路灯、台灯等.
示意图:
如图3.1- 6.
知3-讲
2. 性质
(1)等高的物体垂直于地面放置时,如图3.1-7 所示.
在灯光下,(水平方向)离点光源近的物体的影子短,离点光源远的物体的影子长.
知3-讲
(2)等长的物体平行于地面放置时,如图3.1-8 所示.一般情况下,(竖直方向)离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
(3)在中心投影的情况下,点光源、物体
边缘的点及其影子上的对应点在同一
条直线上.
知3-讲
3. 中心投影点光源的确定方法
形成中心投影的光线是不平行的,即光线是相交的,分别过两个物体的顶端及其影子的顶端作一条直线,这两条直线的交点即为点光源的位置.
知3-讲
示意图:
点光源位置的确定
如图3.1- 9,分别过两棵树的顶端及其树影的顶端作一条直线,两条直线的交点A 即为点光源的位置.
知3-讲
图3.1-10 中的投影不是中心投影的是( )
D
例 5
解题秘方:紧扣“影子的位置情况”和“投影线的方向”进行辨识.
知3-讲
解:A:影子在异侧,是中心投影;
B,C:影子在同侧,作投影线时相交于一点,是中心投影;
D:影子在同侧,作投影线时平行,是平行投影.
知3-讲
教你一招:
判断是中心投影还是平行投影的方法:
●看图中的影子:如果在同侧,则是平行投影或中心投影;如果在异侧,则一定是中心投影.
●作图:过不同物体的顶端及其影子的顶端作直线,若平行,则为平行投影;若相交,则为中心投影.
知4-讲
1. 定义:在平行投影中,如果投影线与投影面互相垂直,就称为“正投影”.
如图3.1-11.
知识点
正投影
4
知4-讲
活用巧记:
投影线垂直投影面,
所得投影正投影;
物体平行投影面,
投影原图是全等;
物体倾斜投影面,
形状大小都会变;
物体垂直投影面,
投影就是点线面.
知4-讲
2. 正投影与平行投影、中心投影的关系
(1)正投影是特殊的平行投影,它不可能是中心投影;
(2)物体的正投影的形状、大小与物体相对于投影面的位置有关,它分物体与投影面平行、倾斜、垂直三种情况.
知4-讲
3. 线段、平面图形、立体图形的正投影
(1)线段的正投影分三种情况:
知4-讲
示意图:
如图3.1- 12.
知4-讲
(2)平面图形的正投影分三种情况:
①当纸板ABCD 平行于投影面时,纸板的正投影与纸板的形状、大小一样. ②当纸板ABCD 倾斜于投影面时,纸板的正投影与纸板的形状、大小不完全一样. ③当纸板ABCD 垂直于投影面时,纸板的正投影为一条线段.
知4-讲
示意图:
知4-讲
(3)立体图形的正投影分为两种情况,如图3.1-14 所示,把正方体的一个面ABCD 放在两个不同的位置:
知4-讲
特别提醒:
●一个立体图形在一个平面上的正投影是一个平面图形,同时,立体图形的正投影可以归结为点、线段及平面图形的正投影.
●物体正投影的形状、大小与物体和投影面的相对位置有关.
●几何体的正投影与平行于投影面且过几何体的最大截面全等.
知4-讲
①当正方体的一个面ABCD 平行于投影面时,如图3.1-14 ①,正方体的正投影为正方形A1B1C1D1,它与正方体的一个面是全等关系.
知4-讲
②当正方体的一个面ABCD 倾斜于投影面,上底面ADHE 垂直于投影面,并且上底面的对角线AH 垂直于投影面时,如图3.1-14 ②,正方体的正投影是矩形E1F1C1D1,这个矩形的长等于正方体的底面对角线的长,矩形的宽等于正方体的棱长. 矩形上、下两边中点的连线A1B1 是正方体的侧棱AB 及它所对的另一条侧棱HG 的投影.
知4-讲
[中考·南宁] 把一个正六棱柱如图3.1-15 摆放,光线由上向下照射此正六棱柱时的正投影是图3.1-16 中的( )
A
例6
知4-讲
示意图:
正六棱柱的正投影
注:立体图形的放置情况多种多样,故其正投影要视放置情况而定.
知4-讲
解题秘方:紧扣“立体图形的正投影”的特征进行识别.
解:由题可知正六棱柱的底面平行于投影面,所以它的正投影是与它的底面全等的正六边形.
知4-讲
如图3.1-18,棱长为 的正方体的侧棱与平面H 平行,其上、下底面的对角线AC,A1C1 与平面H 垂直.
例 7
知4-讲
特别提醒:
●物体的正投影的形状、大小与物体相对于投影面的位置有关,画一般立体图形的正投影的关键是找出平行于投影面的立体图形的最大截面.
●例7 中,侧棱AA1 在投影面上的正投影应为EF这条线段.因为侧棱AA1能够被看到,所以它的正投影应画成实线,不要画成虚线或漏画.
知4-讲
(1)作出正方体六个面在平面H 上的正投影;
解:正方体六个面在平面H 上的正投影如图3.1-19 所示,为矩形MNPQ.
解题秘方:利用“过关键点的投影线”作正投影;
知4-讲
(2)计算正投影的面积.
解:∵正方体的棱长为2 ,∴由勾股定理
得底面对角线的长为 =2,
∴正投影的面积为2× =2 .
解题秘方:紧扣“正投影的线段长等于对应的立体图形的两点间的距离”进行计算.
投 影
物体的
投影
投影线
正投影
平行投影
中心投影
的特征
投影线垂直
于投影面
3.1 投 影
第3章 投影与视图
知识点
投影
知1-讲
1
1. 定义 光线照射物体,会在平面上(如地面、墙壁)留下它的影子,把物体映成它的影子叫作投影. 照射的光线叫投影线,投影所在的平面叫投影面. 物体在投影下的像简称为物体的投影.
特别提醒:
形成投影应具备的条件:
●要有物体存在且物体处于光源与投影面之间;
●要有光线;
●要有一个呈现投影的面, 即投影面(投影面应是平的).
知1-讲
2. 性质
(1)光线是沿直线照射的,因此可以由物体与它的投影确定光线的方向.
(2)不同时刻,物体的影子的方向和大小会发生变化. 在相同的投影线和投影面的情况下,不同形状的物体的投影一般不同.
知1-讲
例 1
下列现象不属于投影的是( )
A. 皮影 B. 树影 C. 手影 D. 素描画
D
解题秘方:紧扣“投影的定义”中的三个条件进行识别.
知1-讲
特别提醒:
●投影是生活中一种常见的现象,没有特殊说明时,本章中的投影问题均指在平面上形成的投影.
●投影现象的特点:光线、物体、投影面的相对位置发生变化,物体的影子就会相应发变化.
知1-讲
解:皮影、树影和手影都符合“用光线照射物体在某个平面上得到的影子”,因此选项A,B,C 都属于投影. 用排除法选D.
知1-讲
如图3.1-1,能近似反映冬季上午10 时你所在学校的旗杆与其影子的位置关系的是( )
例2
C
解题秘方:紧扣“投影的特征”结合生活体验进行判断.
知1-讲
解:冬季上午10 时太阳光下物体的影子应大致为西北方向.
知1-讲
知识储备:
1. 一天内旗杆影子的变化情况;
2. 物体上一点与它的投影的对应点的连线为投影线.
知2-讲
知识点
平行投影
2
1. 定义 由于太阳距离地球很远,从太阳射到地面的光线可以看成平行光线,因此这种投影称为平行投影.
注意:平行投影的投影线都是平行的.
知2-讲
2. 特征
(1)等高的物体垂直于地面放置时,如图3.1-2 ①所示,同一时刻,在太阳光下,它们的影子长相等.
知2-讲
(2)等长的物体平行于地面放置时,如图3.1-2 ②所示,同一时刻,在太阳光下,它们的影子长相等,并且影子的长等于物体本身的长度.
知2-讲
(3)在太阳光下,不同时刻,同一地点、同一物体的影子不仅方向在改变,影子的长度一般也不同,从早晨到傍晚,物体影子的指向是正西→西北→正北→东北→正东(北半球北回归线以北地区). 一天之中,同一物体的影子的长短的变化规律是长→短→最短→短→长.
(4)在太阳光下,不同时刻,同一物体的影子长度不同;同一时刻,不同物体本身的高度与它们的影子长度成正比.
知2-讲
特别提醒:
这一结论可以用相似三角形的性质得到,即
知2-讲
小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的影子不可能是图3.1-3 中的( )
例 3
解题秘方:紧扣“在阳光下,平行且相等的边的平行投影是平行且相等的,也可能是互相重合的”这一特征解答.
A
知2-讲
解题通法:
平行投影中,不同位置、不同时刻,同一物体的影子的大小、形状可能不同,具体形状应视其外在形状及其与光线的夹角而定.平行且相等的边的投影也平行且相等,也可能互相重合.
知2-讲
解:矩形木框在地面上形成的影子应是平行四边形或是一条线段,故不会是梯形.
知2-讲
如图3.1-4,AB 和DE 是直立在地面上的两根立柱,AB=5 m,某一时刻AB 在阳光下的投影BC=3 m.
例4
知2-讲
解法提醒:
画物体的平行投影的方法:
先根据物体的投影确定光线,然后利用两个物体的顶端与各自影子的顶端的连线是一组平行线,过物体顶端作平行线与投影面相交,从而确定其影子.
知2-讲
(1)请你在图中画出此时DE 在阳光下的投影(用线段EF 表示);
解题秘方:紧扣“平行投影的特征”中投影线、影子、物高的特征解答.
知2-讲
解:如图3.1-5,连接AC,过点D 作DF ∥ AC,交直线BE 于点F,则EF 就是DE 的投影.
知2-讲
(2)在测量AB 的投影时,同时测量出DE 在阳光下的投影EF=6 m,请你计算DE 的长.
解题秘方:紧扣“平行投影的特征”中投影线、影子、物高的特征解答.
知2-讲
解:∵在阳光下,同一时刻物高与影长的比相等,∴
∵ AB=5 m,BC=3 m,EF=6 m,
∴ DE= =10m.
知识点
中心投影
知3-讲
3
1. 定义 如果光线从一点发出(如灯泡、电影放映机、幻灯机的光线),这样的投影称为中心投影.
特别提醒:中心投影的光源是点光源,它的光线相交于一点,常见的点光源有手电筒、路灯、台灯等.
示意图:
如图3.1- 6.
知3-讲
2. 性质
(1)等高的物体垂直于地面放置时,如图3.1-7 所示.
在灯光下,(水平方向)离点光源近的物体的影子短,离点光源远的物体的影子长.
知3-讲
(2)等长的物体平行于地面放置时,如图3.1-8 所示.一般情况下,(竖直方向)离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
(3)在中心投影的情况下,点光源、物体
边缘的点及其影子上的对应点在同一
条直线上.
知3-讲
3. 中心投影点光源的确定方法
形成中心投影的光线是不平行的,即光线是相交的,分别过两个物体的顶端及其影子的顶端作一条直线,这两条直线的交点即为点光源的位置.
知3-讲
示意图:
点光源位置的确定
如图3.1- 9,分别过两棵树的顶端及其树影的顶端作一条直线,两条直线的交点A 即为点光源的位置.
知3-讲
图3.1-10 中的投影不是中心投影的是( )
D
例 5
解题秘方:紧扣“影子的位置情况”和“投影线的方向”进行辨识.
知3-讲
解:A:影子在异侧,是中心投影;
B,C:影子在同侧,作投影线时相交于一点,是中心投影;
D:影子在同侧,作投影线时平行,是平行投影.
知3-讲
教你一招:
判断是中心投影还是平行投影的方法:
●看图中的影子:如果在同侧,则是平行投影或中心投影;如果在异侧,则一定是中心投影.
●作图:过不同物体的顶端及其影子的顶端作直线,若平行,则为平行投影;若相交,则为中心投影.
知4-讲
1. 定义:在平行投影中,如果投影线与投影面互相垂直,就称为“正投影”.
如图3.1-11.
知识点
正投影
4
知4-讲
活用巧记:
投影线垂直投影面,
所得投影正投影;
物体平行投影面,
投影原图是全等;
物体倾斜投影面,
形状大小都会变;
物体垂直投影面,
投影就是点线面.
知4-讲
2. 正投影与平行投影、中心投影的关系
(1)正投影是特殊的平行投影,它不可能是中心投影;
(2)物体的正投影的形状、大小与物体相对于投影面的位置有关,它分物体与投影面平行、倾斜、垂直三种情况.
知4-讲
3. 线段、平面图形、立体图形的正投影
(1)线段的正投影分三种情况:
知4-讲
示意图:
如图3.1- 12.
知4-讲
(2)平面图形的正投影分三种情况:
①当纸板ABCD 平行于投影面时,纸板的正投影与纸板的形状、大小一样. ②当纸板ABCD 倾斜于投影面时,纸板的正投影与纸板的形状、大小不完全一样. ③当纸板ABCD 垂直于投影面时,纸板的正投影为一条线段.
知4-讲
示意图:
知4-讲
(3)立体图形的正投影分为两种情况,如图3.1-14 所示,把正方体的一个面ABCD 放在两个不同的位置:
知4-讲
特别提醒:
●一个立体图形在一个平面上的正投影是一个平面图形,同时,立体图形的正投影可以归结为点、线段及平面图形的正投影.
●物体正投影的形状、大小与物体和投影面的相对位置有关.
●几何体的正投影与平行于投影面且过几何体的最大截面全等.
知4-讲
①当正方体的一个面ABCD 平行于投影面时,如图3.1-14 ①,正方体的正投影为正方形A1B1C1D1,它与正方体的一个面是全等关系.
知4-讲
②当正方体的一个面ABCD 倾斜于投影面,上底面ADHE 垂直于投影面,并且上底面的对角线AH 垂直于投影面时,如图3.1-14 ②,正方体的正投影是矩形E1F1C1D1,这个矩形的长等于正方体的底面对角线的长,矩形的宽等于正方体的棱长. 矩形上、下两边中点的连线A1B1 是正方体的侧棱AB 及它所对的另一条侧棱HG 的投影.
知4-讲
[中考·南宁] 把一个正六棱柱如图3.1-15 摆放,光线由上向下照射此正六棱柱时的正投影是图3.1-16 中的( )
A
例6
知4-讲
示意图:
正六棱柱的正投影
注:立体图形的放置情况多种多样,故其正投影要视放置情况而定.
知4-讲
解题秘方:紧扣“立体图形的正投影”的特征进行识别.
解:由题可知正六棱柱的底面平行于投影面,所以它的正投影是与它的底面全等的正六边形.
知4-讲
如图3.1-18,棱长为 的正方体的侧棱与平面H 平行,其上、下底面的对角线AC,A1C1 与平面H 垂直.
例 7
知4-讲
特别提醒:
●物体的正投影的形状、大小与物体相对于投影面的位置有关,画一般立体图形的正投影的关键是找出平行于投影面的立体图形的最大截面.
●例7 中,侧棱AA1 在投影面上的正投影应为EF这条线段.因为侧棱AA1能够被看到,所以它的正投影应画成实线,不要画成虚线或漏画.
知4-讲
(1)作出正方体六个面在平面H 上的正投影;
解:正方体六个面在平面H 上的正投影如图3.1-19 所示,为矩形MNPQ.
解题秘方:利用“过关键点的投影线”作正投影;
知4-讲
(2)计算正投影的面积.
解:∵正方体的棱长为2 ,∴由勾股定理
得底面对角线的长为 =2,
∴正投影的面积为2× =2 .
解题秘方:紧扣“正投影的线段长等于对应的立体图形的两点间的距离”进行计算.
投 影
物体的
投影
投影线
正投影
平行投影
中心投影
的特征
投影线垂直
于投影面
