湘教版九年级数学下册 4.2.1概率的概念课件(共23张PPT)
文档属性
| 名称 | 湘教版九年级数学下册 4.2.1概率的概念课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
4.2 概率及其计算
第4章 概率
4.2.1 概率的概念
知识点
概率
知1-讲
1
1. 概率
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A 发生的概率,记为P(A).
知1-讲
2. 概率的计算
一般地,如果在一次试验中,有n 种可能的结果,其中每一种结果发生的可能性相等,那么出现每一种结果的概率都是 . 如果事件A 包含其中的m 种可能的结果,那么事件A 发生的概率P(A)=
0 ≤ P(A)≤ 1.
当A 为必然事件时,P(A)=1;
当A 为不可能事件时,P(A)=0.
知1-讲
特别提醒:
1. 使用概率公式计算的试验需具有以下特点:
(1)每一次试验中,可能出现的结果是有限个;
(2)每一次试验中,各种结果出现的可能性相等.
2. 随机事件的概率从数量上反映了随机事件发生的可能性的大小,概率是一个常数,不会受重复试验结果的影响.
3. 概率大,并不能说明事件A 一定发生;反之概率小,并不能说明事件A 一定不发生.
4. 同一事件,发生的概率和不发生的概率之和为1.
知1-讲
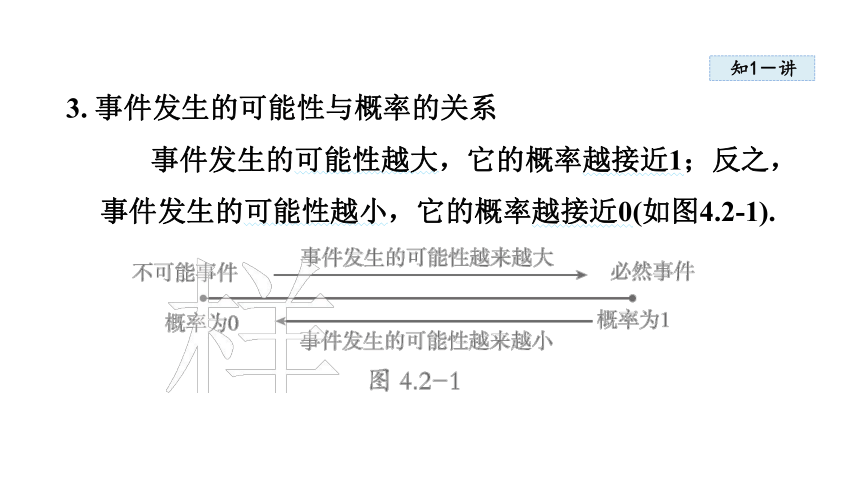
3. 事件发生的可能性与概率的关系
事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0(如图4.2-1).
知1-讲
例 1
[中考·衡阳] 已知抛一枚均匀硬币正面朝上的概率为 ,下列说法错误的是( )
A. 连续抛一枚均匀硬币2 次必有1 次正面朝上
B. 连续抛一枚均匀硬币10 次都有可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100 次出现正面朝上50 次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
A
知1-讲
特别提醒:
概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,机会大也不一定发生,机会小也有可能发生.
知1-讲
解题秘方:紧扣概率定义中概率是刻画随机事件发生可能性大小的数值进行说明.
方法点拨:
理解随机事件的概率的定义时,关键要扣住关键词语,如“必有”“都有”“一定”等等.
知1-讲
解:A. 连续抛一枚均匀硬币2 次必有1 次正面朝上,不正确,有可能2次都正面朝上,也有可能都反面朝上,故此选项错误;
B. 连续抛一枚均匀硬币10 次都有可能正面朝上,是一个随机事件,有可能发生,故此选项正确;
C. 大量反复抛一枚均匀硬币,平均每100 次出现正面朝上50 次,也有可能发生,故此选项正确;
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的,概率均为 ,故此选项正确.
知1-讲
[中考·南京] 甲口袋中有2 个白球、1 个红球,乙口袋中有1 个白球、1 个红球,这些球除颜色外无其他差别,分别从每个口袋中随机摸出1 个球.
例2
知1-讲
解题秘方:紧扣概率公式——“所求事件包含的可能结果数与所有可能出现的结果数的比”进行计算,求解比较.
解题通法:
利用公式P(A)= 求概率的方法:
利用公式P(A)= 直接计算概率需要满足两个条件:一是所有可能出现的结果是有限个;
二是每种结果出现的可能性相等.求等可能事件的概率时,首先求出所有可能出现的结果数n和所求事件A包含的可能结果数m,再运用概率公式P(A)= 计算出所求事件A发生的概率.
知1-讲
P(摸出的2 个球颜色相同)=
P(摸出的2 个球颜色不相同)=
P(摸出的2 个球中至少有1 个红球)=
P(摸出的2 个球中至少有1 个白球)=
知1-讲
(1)求摸出的2 个球都是白球的概率.
解:把甲口袋中的2 个白球、1 个红球分别记为白1,白2,红1,把乙口袋中的 1 个白球、1 个红球分别记为白3,红2,分别从每个口袋中随机摸出1 个球,所有可能的结果有:(白1,白3),(白1,红2),(白2,
白3),(白2,红2),(红1,白3),(红1,红2),共有6 种等可能的结果,其中摸出的2 个球都是白球的结果有2 种,∴ P(摸出的2 个球都是白球)= .
知1-讲
(2)下列事件中,概率最大的是( )
A. 摸出的2 个球颜色相同
B. 摸出的2 个球颜色不相同
C. 摸出的2 个球中至少有1 个红球
D. 摸出的2 个球中至少有1 个白球
D
知2-讲
知识点
概率的应用
2
1. 几何图形中的概率
设某几何图形的面积为S,其中事件A 发生所在区域的面积为S′,由于对这个几何图形内的每个点,事件发生的可能性是相等的,因此我们可以得到事件A 发生的概率P(A)= .
知2-讲
2. 计算简单事件的概率的主要类型
(1)个数类型:如摸球、掷骰子等,可以表示出所有可能出现的结果;
(2)面积类型:如果随机试验是向A 区域内掷一点,那么掷在区域B(B在A 内)内的概率P= .
特别提醒:
当A区域内各个区域的面积都相等时,则面积类型可转化为个数类型来进行概率计算.
知2-讲
[中考·随州] 正方形ABCD 的边长为2,以各边为直径在正方形内画半圆,得到如图4.2-2 的阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )
例 3
A
知2-讲
解题秘方:紧扣各区域的面积是否完全相等选择公式类型.
特别提醒:
当事件出现的可能结果不能用数量来表示时, 往往采用P(A)= 来计算事件A 发生的概率.
知2-讲
解::因为正方形ABCD 的面积为22=4,阴影部分的面积为4 个半圆形的面积和与正方形ABCD 的面积之差,即4× -4=2π-4,所以米粒落在阴影部分的概率为 .
知2-讲
如图4.2-3 的六边形广场由6 个大小完全相同的灰色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在灰色正三角形区域的概率为______ .
例4
知2-讲
解题秘方:共有6 个完全相同的正三角形,小鸟落在每个正三角形上的可能性相等.
解法提醒:
只要事件的各种结果出现的可能性相等,且所有可能出现的结果数有限,都可用P(A)= 求事件的概率.当无法用个数量化时,也可用P(A)= 求事件的概率.
知2-讲
解:因为小鸟落在每个正三角形上的可能性相等,所以共有6种等可能的结果,其中落在灰色正三角形区域的结果有2 种,所以刚好落在灰色正三角形区域的概率P= .
概率的概念
概率
确定性事
件的概率
随机事件的概率:0 < P(A) < 1
必然事件的概率为1
不可能事件的概率为0
4.2 概率及其计算
第4章 概率
4.2.1 概率的概念
知识点
概率
知1-讲
1
1. 概率
一般地,对于一个随机事件A,我们把刻画其发生可能性大小的数值,称为随机事件A 发生的概率,记为P(A).
知1-讲
2. 概率的计算
一般地,如果在一次试验中,有n 种可能的结果,其中每一种结果发生的可能性相等,那么出现每一种结果的概率都是 . 如果事件A 包含其中的m 种可能的结果,那么事件A 发生的概率P(A)=
0 ≤ P(A)≤ 1.
当A 为必然事件时,P(A)=1;
当A 为不可能事件时,P(A)=0.
知1-讲
特别提醒:
1. 使用概率公式计算的试验需具有以下特点:
(1)每一次试验中,可能出现的结果是有限个;
(2)每一次试验中,各种结果出现的可能性相等.
2. 随机事件的概率从数量上反映了随机事件发生的可能性的大小,概率是一个常数,不会受重复试验结果的影响.
3. 概率大,并不能说明事件A 一定发生;反之概率小,并不能说明事件A 一定不发生.
4. 同一事件,发生的概率和不发生的概率之和为1.
知1-讲
3. 事件发生的可能性与概率的关系
事件发生的可能性越大,它的概率越接近1;反之,事件发生的可能性越小,它的概率越接近0(如图4.2-1).
知1-讲
例 1
[中考·衡阳] 已知抛一枚均匀硬币正面朝上的概率为 ,下列说法错误的是( )
A. 连续抛一枚均匀硬币2 次必有1 次正面朝上
B. 连续抛一枚均匀硬币10 次都有可能正面朝上
C. 大量反复抛一枚均匀硬币,平均每100 次出现正面朝上50 次
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的
A
知1-讲
特别提醒:
概率是反映事件发生机会的大小的概念,只是表示发生的机会的大小,机会大也不一定发生,机会小也有可能发生.
知1-讲
解题秘方:紧扣概率定义中概率是刻画随机事件发生可能性大小的数值进行说明.
方法点拨:
理解随机事件的概率的定义时,关键要扣住关键词语,如“必有”“都有”“一定”等等.
知1-讲
解:A. 连续抛一枚均匀硬币2 次必有1 次正面朝上,不正确,有可能2次都正面朝上,也有可能都反面朝上,故此选项错误;
B. 连续抛一枚均匀硬币10 次都有可能正面朝上,是一个随机事件,有可能发生,故此选项正确;
C. 大量反复抛一枚均匀硬币,平均每100 次出现正面朝上50 次,也有可能发生,故此选项正确;
D. 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的,概率均为 ,故此选项正确.
知1-讲
[中考·南京] 甲口袋中有2 个白球、1 个红球,乙口袋中有1 个白球、1 个红球,这些球除颜色外无其他差别,分别从每个口袋中随机摸出1 个球.
例2
知1-讲
解题秘方:紧扣概率公式——“所求事件包含的可能结果数与所有可能出现的结果数的比”进行计算,求解比较.
解题通法:
利用公式P(A)= 求概率的方法:
利用公式P(A)= 直接计算概率需要满足两个条件:一是所有可能出现的结果是有限个;
二是每种结果出现的可能性相等.求等可能事件的概率时,首先求出所有可能出现的结果数n和所求事件A包含的可能结果数m,再运用概率公式P(A)= 计算出所求事件A发生的概率.
知1-讲
P(摸出的2 个球颜色相同)=
P(摸出的2 个球颜色不相同)=
P(摸出的2 个球中至少有1 个红球)=
P(摸出的2 个球中至少有1 个白球)=
知1-讲
(1)求摸出的2 个球都是白球的概率.
解:把甲口袋中的2 个白球、1 个红球分别记为白1,白2,红1,把乙口袋中的 1 个白球、1 个红球分别记为白3,红2,分别从每个口袋中随机摸出1 个球,所有可能的结果有:(白1,白3),(白1,红2),(白2,
白3),(白2,红2),(红1,白3),(红1,红2),共有6 种等可能的结果,其中摸出的2 个球都是白球的结果有2 种,∴ P(摸出的2 个球都是白球)= .
知1-讲
(2)下列事件中,概率最大的是( )
A. 摸出的2 个球颜色相同
B. 摸出的2 个球颜色不相同
C. 摸出的2 个球中至少有1 个红球
D. 摸出的2 个球中至少有1 个白球
D
知2-讲
知识点
概率的应用
2
1. 几何图形中的概率
设某几何图形的面积为S,其中事件A 发生所在区域的面积为S′,由于对这个几何图形内的每个点,事件发生的可能性是相等的,因此我们可以得到事件A 发生的概率P(A)= .
知2-讲
2. 计算简单事件的概率的主要类型
(1)个数类型:如摸球、掷骰子等,可以表示出所有可能出现的结果;
(2)面积类型:如果随机试验是向A 区域内掷一点,那么掷在区域B(B在A 内)内的概率P= .
特别提醒:
当A区域内各个区域的面积都相等时,则面积类型可转化为个数类型来进行概率计算.
知2-讲
[中考·随州] 正方形ABCD 的边长为2,以各边为直径在正方形内画半圆,得到如图4.2-2 的阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )
例 3
A
知2-讲
解题秘方:紧扣各区域的面积是否完全相等选择公式类型.
特别提醒:
当事件出现的可能结果不能用数量来表示时, 往往采用P(A)= 来计算事件A 发生的概率.
知2-讲
解::因为正方形ABCD 的面积为22=4,阴影部分的面积为4 个半圆形的面积和与正方形ABCD 的面积之差,即4× -4=2π-4,所以米粒落在阴影部分的概率为 .
知2-讲
如图4.2-3 的六边形广场由6 个大小完全相同的灰色和白色正三角形组成,一只小鸟在广场上随机停留,刚好落在灰色正三角形区域的概率为______ .
例4
知2-讲
解题秘方:共有6 个完全相同的正三角形,小鸟落在每个正三角形上的可能性相等.
解法提醒:
只要事件的各种结果出现的可能性相等,且所有可能出现的结果数有限,都可用P(A)= 求事件的概率.当无法用个数量化时,也可用P(A)= 求事件的概率.
知2-讲
解:因为小鸟落在每个正三角形上的可能性相等,所以共有6种等可能的结果,其中落在灰色正三角形区域的结果有2 种,所以刚好落在灰色正三角形区域的概率P= .
概率的概念
概率
确定性事
件的概率
随机事件的概率:0 < P(A) < 1
必然事件的概率为1
不可能事件的概率为0
