湘教版九年级数学下册 4.1随机事件与可能性课件(共18张PPT)
文档属性
| 名称 | 湘教版九年级数学下册 4.1随机事件与可能性课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 16:13:17 | ||
图片预览





文档简介
(共18张PPT)
4.1 随机事件与可能性
第4章 概率
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
事件的认识
事件发生的可能性
知识点
事件的认识
知1-讲
1
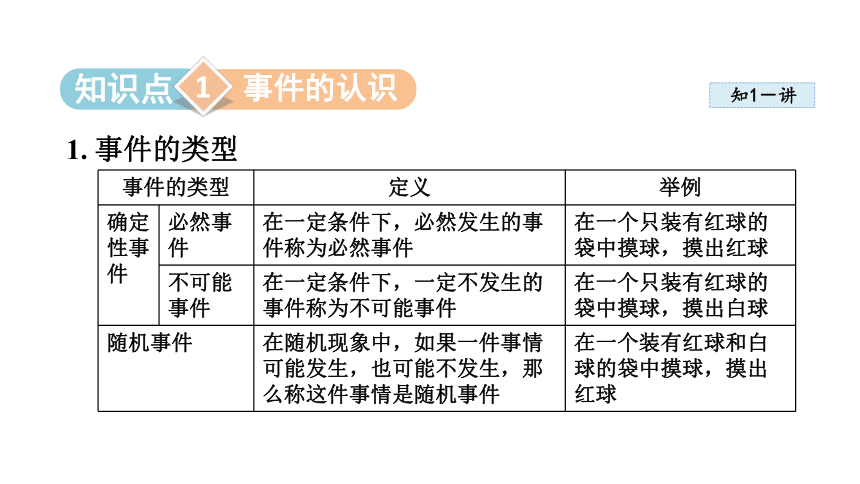
1. 事件的类型
事件的类型 定义 举例
确定性事件 必然事件 在一定条件下,必然发生的事件称为必然事件 在一个只装有红球的袋中摸球,摸出红球
不可能事件 在一定条件下,一定不发生的事件称为不可能事件 在一个只装有红球的袋中摸球,摸出白球
随机事件 在随机现象中,如果一件事情可能发生,也可能不发生,那么称这件事情是随机事件 在一个装有红球和白球的袋中摸球,摸出红球
知1-讲
2. 确定性事件:必然事件与不可能事件统称为确定性事件.
3.“一定条件下”的意义:必然事件、不可能事件的定义中所说的“一定条件下”是指试验在相同的条件下进行,不同的条件下可能会导致不同的事件归类.
如:标准大气压下,水加热到100℃沸腾是必然事件,但当气压高于标准大气压时,水的沸点提高,水加热到100℃沸腾就不是必然事件了.
知1-讲
特别提醒:
1. 确定性事件在事件发生前是可以预知结果的,随机事件在事件发生前是不能预知结果的,随机事件也称为“偶然性事件”.
2. 按事件的确定性划分,事件可划分为确定性事件和不确定性事件(即随机事件).
3. 一般地,描述已被确定的真理或者客观存在的事实的事件是必然事件;描述违背已被确定的真理或者违背客观存在的事实的事件是不可能事件.
知1-讲
例 1
指出下列事件中,哪些是必然事件,哪些是随机事件,哪些是不可能事件.
(1)掷一枚质地均匀的硬币,正面朝上;
(2)买一张彩票,中一百万元;
(3)x2+1>0;
(4)任意买一张电影票,座位号是双号;
(5) 向空中抛一枚质地均匀的硬币,硬币不向地面掉落.
知1-讲
解题秘方:判断一个事件的类型紧扣两点:①是否可能发生;②可能发生的情况是否唯一.
解法提醒:
判断一个事件的类型的方法:
要从其定义出发,同时也要联系理论及生活的相关常识来判断.注意必然事件和不可能事件都是事先可以确定的,一定发生的是必然事件,一定不发生的是不可能事件,否则就是机事件.
知1-讲
解:(3)是必然事件;(5)是不可能事件;(1)(2)(4)是随机事件.
知2-讲
知识点
事件发生的可能性
2
1. 一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同.
知2-讲
2.事件发生的可能性
(1)必然事件:试验中必然发生的事件,其发生的可能性为100% 或1;
(2)不可能事件:试验中不可能发生的事件,其发生的可能性为0;
(3)随机事件:试验中可能发生也可能不发生的事件,其发生的可能性介于0 和1 之间.
知2-讲
3. 描述随机事件发生的可能性大小的常用语“可能性极小”“不大可能”“可能”“很可能”“可能性极大”等.
知2-讲
方法点拨:
判断随机事件发生的可能性大小的方法:
先要准确地找出所有可能出现的结果数,
然后分情况,看每种情况包含的结果数与所有可能出现的结果数的比例大小. 比例越大,则这种情况发生的可能性越大.
知2-讲
一个不透明的口袋中有7 个红球,5 个黄球,4 个绿球,这些球除颜色外没有其他区别,现从中任意摸出1 个球.
例2
知2-讲
(1)你认为摸到哪种颜色的球的可能性最大?
解题秘方:口袋中哪种颜色的球最多,则摸到这种颜色的球的可能性就最大.
解:摸到红球的可能性最大.
知2-讲
(2)如果要使摸到绿球的可能性最大,那么需要在这个口袋中至少再放入多少个绿球?请简要说明理由.
解题秘方:口袋中哪种颜色的球最多,则摸到这种颜色的球的可能性就最大.
知2-讲
解:如至少再放入4 个绿球.
理由:当绿球的个数最多时,摸到绿球的可能性最大,因为原来口袋中红球的个数最多,有7 个,所以至少要再放入4 个绿球.
知2-讲
警示误区:
要使摸到绿球的可能性最大,应保证口袋中绿球的个数最多,所以至少再放入4个绿球,此处容易错误地认为至少再放入3个绿球,当放入3个绿球后,红球和绿球一样多,此时摸到绿球的可能性与摸到红球的可能性一样大,并不能保证摸到绿球的可能性最大.
随机事件与可能性
事件
确定性事件
随机事件
必然事件
不可能事件
事件可能
性大小
4.1 随机事件与可能性
第4章 概率
逐点
导讲练
课堂小结
作业提升
课时讲解
1
课时流程
2
事件的认识
事件发生的可能性
知识点
事件的认识
知1-讲
1
1. 事件的类型
事件的类型 定义 举例
确定性事件 必然事件 在一定条件下,必然发生的事件称为必然事件 在一个只装有红球的袋中摸球,摸出红球
不可能事件 在一定条件下,一定不发生的事件称为不可能事件 在一个只装有红球的袋中摸球,摸出白球
随机事件 在随机现象中,如果一件事情可能发生,也可能不发生,那么称这件事情是随机事件 在一个装有红球和白球的袋中摸球,摸出红球
知1-讲
2. 确定性事件:必然事件与不可能事件统称为确定性事件.
3.“一定条件下”的意义:必然事件、不可能事件的定义中所说的“一定条件下”是指试验在相同的条件下进行,不同的条件下可能会导致不同的事件归类.
如:标准大气压下,水加热到100℃沸腾是必然事件,但当气压高于标准大气压时,水的沸点提高,水加热到100℃沸腾就不是必然事件了.
知1-讲
特别提醒:
1. 确定性事件在事件发生前是可以预知结果的,随机事件在事件发生前是不能预知结果的,随机事件也称为“偶然性事件”.
2. 按事件的确定性划分,事件可划分为确定性事件和不确定性事件(即随机事件).
3. 一般地,描述已被确定的真理或者客观存在的事实的事件是必然事件;描述违背已被确定的真理或者违背客观存在的事实的事件是不可能事件.
知1-讲
例 1
指出下列事件中,哪些是必然事件,哪些是随机事件,哪些是不可能事件.
(1)掷一枚质地均匀的硬币,正面朝上;
(2)买一张彩票,中一百万元;
(3)x2+1>0;
(4)任意买一张电影票,座位号是双号;
(5) 向空中抛一枚质地均匀的硬币,硬币不向地面掉落.
知1-讲
解题秘方:判断一个事件的类型紧扣两点:①是否可能发生;②可能发生的情况是否唯一.
解法提醒:
判断一个事件的类型的方法:
要从其定义出发,同时也要联系理论及生活的相关常识来判断.注意必然事件和不可能事件都是事先可以确定的,一定发生的是必然事件,一定不发生的是不可能事件,否则就是机事件.
知1-讲
解:(3)是必然事件;(5)是不可能事件;(1)(2)(4)是随机事件.
知2-讲
知识点
事件发生的可能性
2
1. 一般地,随机事件发生的可能性是有大小的,不同的随机事件发生的可能性的大小有可能不同.
知2-讲
2.事件发生的可能性
(1)必然事件:试验中必然发生的事件,其发生的可能性为100% 或1;
(2)不可能事件:试验中不可能发生的事件,其发生的可能性为0;
(3)随机事件:试验中可能发生也可能不发生的事件,其发生的可能性介于0 和1 之间.
知2-讲
3. 描述随机事件发生的可能性大小的常用语“可能性极小”“不大可能”“可能”“很可能”“可能性极大”等.
知2-讲
方法点拨:
判断随机事件发生的可能性大小的方法:
先要准确地找出所有可能出现的结果数,
然后分情况,看每种情况包含的结果数与所有可能出现的结果数的比例大小. 比例越大,则这种情况发生的可能性越大.
知2-讲
一个不透明的口袋中有7 个红球,5 个黄球,4 个绿球,这些球除颜色外没有其他区别,现从中任意摸出1 个球.
例2
知2-讲
(1)你认为摸到哪种颜色的球的可能性最大?
解题秘方:口袋中哪种颜色的球最多,则摸到这种颜色的球的可能性就最大.
解:摸到红球的可能性最大.
知2-讲
(2)如果要使摸到绿球的可能性最大,那么需要在这个口袋中至少再放入多少个绿球?请简要说明理由.
解题秘方:口袋中哪种颜色的球最多,则摸到这种颜色的球的可能性就最大.
知2-讲
解:如至少再放入4 个绿球.
理由:当绿球的个数最多时,摸到绿球的可能性最大,因为原来口袋中红球的个数最多,有7 个,所以至少要再放入4 个绿球.
知2-讲
警示误区:
要使摸到绿球的可能性最大,应保证口袋中绿球的个数最多,所以至少再放入4个绿球,此处容易错误地认为至少再放入3个绿球,当放入3个绿球后,红球和绿球一样多,此时摸到绿球的可能性与摸到红球的可能性一样大,并不能保证摸到绿球的可能性最大.
随机事件与可能性
事件
确定性事件
随机事件
必然事件
不可能事件
事件可能
性大小
