有理数的乘方
图片预览









文档简介
(共35张PPT)
a
(1)边长为 的正方形的面积是 ,简记作 ,读作 的平方(或二次方)
(2)棱长为 的正方体的体积是 ,简记作 ,读作 的立方(或三次方)
2个 相加可记为:
边长为 的正方形的面积可记为:
3个 相加可为:
棱长为 的正方体的体积可记为:
个 相加可记为:
个 相乘又可记为:
an
a
a·a
a
a·a·a
2
2×2
2
2
2×2×2
2
a
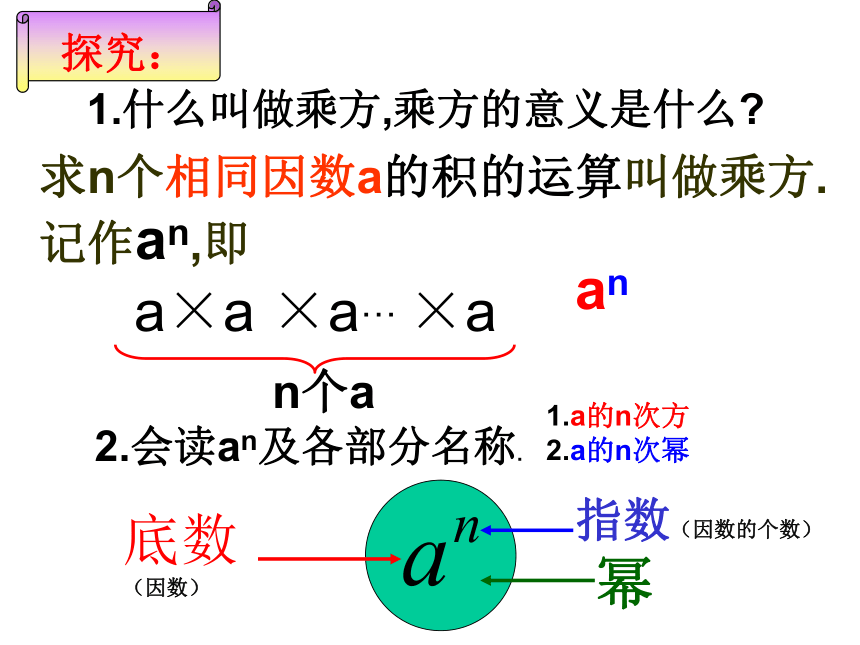
1.什么叫做乘方,乘方的意义是什么
指数(因数的个数)
幂
底数
(因数)
求n个相同因数a的积的运算叫做乘方.记作an,即
a×a ×a… ×a
n个a
an
探究:
2.会读an及各部分名称.
1.a的n次方
2.a的n次幂
1.把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2. (-1.3)(-1.3)(-1.3)(-1.3)
4. m·m ·m ·… ·m
a个
4、
(- )3
赏析例一
计算:
1、 (-4)3
2、(-2)4
2
3
(- )2
1
5
3、
你发现负数的幂的符号有什么规律?
解: 1、(-4)3=
-
8
27
2
3
(- )3
(- )2
1
5
2
3
(- )
2
3
(- )
2
3
(- )
(- )
1
5
(- )
1
5
=
× ×
=
=
×
=
1
25
3、
4、
2、(-2)4=(-2) ×(-2) ×(-2) ×(-2)=16
(-4) ×(-4) ×(-4)
=-64
当指数是——数时,负数的幂是—数。
当指数是——数时,负数的幂是—数。
奇
负
偶
正
4、
( )3
变形训练
计算:
1、 43
2、24
2
3
( )2
1
5
3、
你发现正数和0的幂有什么规律?
5、 05
=64
=16
=
8
27
=
1
25
=0
正数的任何次幂都是正数,
0的任何正整数次幂都是0。
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂是负数;
(3)0的任何次幂等于零; 1的任何次幂等于1.
乘方运算的符号规律
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ;
对
错
错
错
3.计算:
1、(-1)10
2、(-1)7
3、83
6、(- )4
1
2
5、
4、-24
2
3
3
= -1
= 1
= 512
=
16
1
=-16
=—
8
3
4.-32与(-3)2 结果相等吗?
- 32读作的32相反数,结果是-9;而(-3)2 读作 -3的平方,结果是9 。
5.请你说说下列各数表示什么?它们一样吗?
(1)23 与 32
(2) 与
注意:当底数是负数或分数
时,底数一定要加上括弧,这
也是辩认底数的方法.
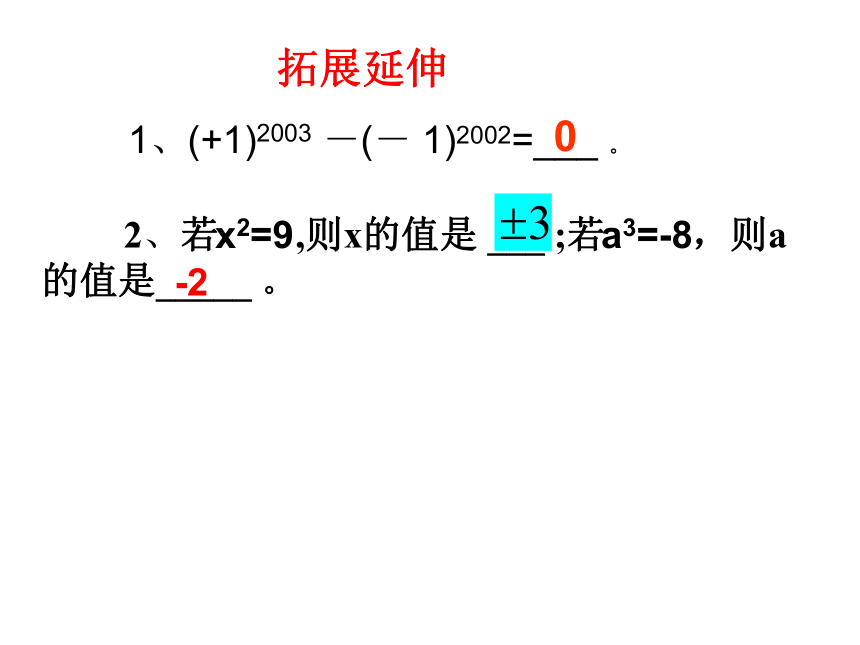
2、若 ,则x的值是 ___ ;若 ,则a的值是_____ 。
1、(+1)2003 -(- 1)2002=___ 。
0
-2
x2=9
a3=-8
拓展延伸
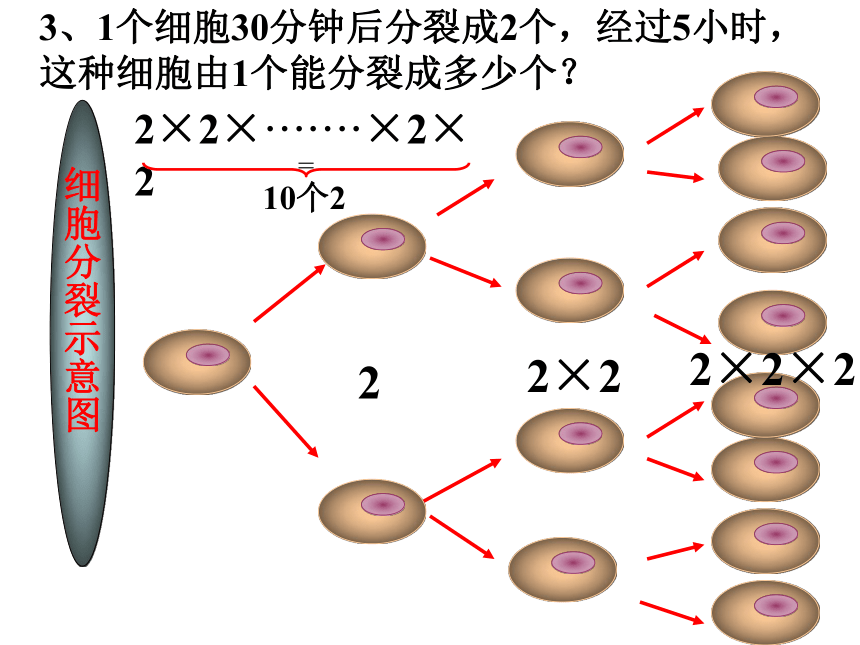
细胞分裂示意图
3、1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
课堂小结
1、乘方的概念:求n个相同因数的积的运算叫做乘方。
2、乘方符号的确定:
an
底数
幂(乘方的结果叫做幂)
指数
an读法:a的n次方或a的n次幂
负数的奇次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都是0。
复 习
填空:
2、式子 表示的意义是_________。
1、 在 中,a叫做____,n叫做____,
乘方的结果叫做____。
底数
指数
幂
n个a相乘
3. (-4)8 __ 0 (-4)9__ 0
>
<
想一想
(1) 和 的有什
么不同?运算结果是否相同?
(2) 和 呢?
(-1)
10
8
3
(-5)
3
0.1
3
(-10)4
(-10)5
(-1)
7
练习
1、计算
(1) (2) (3) (4)
(5) (6) (7) (8)
(-1)
7
(-1)
10
8
3
(-5)
3
0.1
3
1
2
—
(- )
4
(-10)4
(-10)5
1
2
—
(- )
4
解:
=1
=-1
=512
=-125
=0.001
1
16
= —
=10000
=-100000
运用新知 体会成功:
(1)、(-5)3 (2)、
(3)、5×23 (4)、(5×2)3
(5)、(-2)2 ×(-3)2
(6)、(-2)3÷ 22
-125
256
81
40
1000
36
-2
4.计算:
先乘方、再乘除
(4)
1.先乘方、再乘除、最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
2×(-3)3-4×(-3)+15
(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2)
例3 计算
解(1)第①行数是
-2,(-2)2 ,(-2)3 ,(-2)4 , …
(2)对比①②两行中位置对应的数,你有什么发现?第②行数是第①行相应的数加2,即
-2+2,(-2)2+2,(-2)3+2,(-2)4+2,…
例4 观察下面三行数:
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
(1)第①行数按什么规律排列
(2)第②③行数与第第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和。
对比①③两行中位置对应的数,你有什么发现?第③行是第①行相应的数的0.5倍,即
-2X0.5,(-2)2X0.5,(-2)3X0.5,(-2)4X0.5,…
(3)每行数中的第10个数的和是
(-2)10+[(-2)10+2]+(-2)10X0.5
=1024+(1024+2)+1024X0.5
=1024+1026+512=2562
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
练习
计算:
(1)(-1)10×2+(-2)3÷4
(2)
思路:先算乘方,再算乘除,再算加减
解:原式=1×2+(-8)÷4
=2+(-2)=0
思路:先算乘方,再算乘法,再算减
思路:先算括号内的运算,再从左到右
解:原式=10000+(16-12X2)
=10000-8=9992
(4)(-10)4+[(-4)2-(3+32)X2]
(3)
课堂小结
1、乘方的概念:求n个相同因数的积的运算叫做乘方。
2、乘方符号的确定:
an
底数
幂(乘方的结果叫做幂)
指数
an读法:a的n次方或a的n次幂
负数的奇次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都是0。
有理数的混合运算法则
1.先乘方、再乘除、最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
3.若a为任意有理数,则a2一定是( )
A.正数 B.负数
C.非负数 D.非正数
B
C
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条。如图所示:
第1次
第2次
第3次
这样捏合到第 次后可拉出128根面条。
生活数学
≈
≈
异想天开
珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?
这张纸对折30次后能超过珠穆朗玛峰吗?
有一张厚度是0.1毫米的纸,将它对折1 次后,厚度为2×0.1毫米。
(1)对折2次后,厚度为多少毫米?
(2)对折30次后,厚度为多少毫米?
1次
2次
30次
如果一层楼按高3米计算,把足够长的厚0.1毫米的纸继续折叠20次约有104米高,有34层楼高;继续折叠30次后有10万多米高,有12个珠穆朗玛峰高。
分析:(1)0.1毫米×220=0.1毫米×1048576
=104.8576米
34×3=102米
(2)0.1毫米×230=0.1毫米×1073741824
=107374.1824米
8844.43 ×12=106133.16
这下你该
相信了吧!
古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
事实上,按照这个大臣的要求,放满一个棋盘上的64个格子需要1+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616
巴衣老爷说:你能每天给我10元钱,一共给我20年吗?阿凡提说:尊敬的巴衣老爷,如果你能第一天给我1毛钱,第二天给我2毛钱,第三天给我4毛钱,以此类推,一直给20天,那我就答应你的要求!巴衣老爷眼珠子一转说:那好吧!亲爱的同学们:你知道阿凡提和巴衣老爷谁得到的钱多?
a
(1)边长为 的正方形的面积是 ,简记作 ,读作 的平方(或二次方)
(2)棱长为 的正方体的体积是 ,简记作 ,读作 的立方(或三次方)
2个 相加可记为:
边长为 的正方形的面积可记为:
3个 相加可为:
棱长为 的正方体的体积可记为:
个 相加可记为:
个 相乘又可记为:
an
a
a·a
a
a·a·a
2
2×2
2
2
2×2×2
2
a
1.什么叫做乘方,乘方的意义是什么
指数(因数的个数)
幂
底数
(因数)
求n个相同因数a的积的运算叫做乘方.记作an,即
a×a ×a… ×a
n个a
an
探究:
2.会读an及各部分名称.
1.a的n次方
2.a的n次幂
1.把下列各式写成乘方运算的形式,并指出底数,指数各是什么
1. 5×5×5×5×5
2. (-1.3)(-1.3)(-1.3)(-1.3)
4. m·m ·m ·… ·m
a个
4、
(- )3
赏析例一
计算:
1、 (-4)3
2、(-2)4
2
3
(- )2
1
5
3、
你发现负数的幂的符号有什么规律?
解: 1、(-4)3=
-
8
27
2
3
(- )3
(- )2
1
5
2
3
(- )
2
3
(- )
2
3
(- )
(- )
1
5
(- )
1
5
=
× ×
=
=
×
=
1
25
3、
4、
2、(-2)4=(-2) ×(-2) ×(-2) ×(-2)=16
(-4) ×(-4) ×(-4)
=-64
当指数是——数时,负数的幂是—数。
当指数是——数时,负数的幂是—数。
奇
负
偶
正
4、
( )3
变形训练
计算:
1、 43
2、24
2
3
( )2
1
5
3、
你发现正数和0的幂有什么规律?
5、 05
=64
=16
=
8
27
=
1
25
=0
正数的任何次幂都是正数,
0的任何正整数次幂都是0。
(1)正数的任何次幂是正数;
(2)负数的偶次幂是正数;负数的奇次幂是负数;
(3)0的任何次幂等于零; 1的任何次幂等于1.
乘方运算的符号规律
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ;
对
错
错
错
3.计算:
1、(-1)10
2、(-1)7
3、83
6、(- )4
1
2
5、
4、-24
2
3
3
= -1
= 1
= 512
=
16
1
=-16
=—
8
3
4.-32与(-3)2 结果相等吗?
- 32读作的32相反数,结果是-9;而(-3)2 读作 -3的平方,结果是9 。
5.请你说说下列各数表示什么?它们一样吗?
(1)23 与 32
(2) 与
注意:当底数是负数或分数
时,底数一定要加上括弧,这
也是辩认底数的方法.
2、若 ,则x的值是 ___ ;若 ,则a的值是_____ 。
1、(+1)2003 -(- 1)2002=___ 。
0
-2
x2=9
a3=-8
拓展延伸
细胞分裂示意图
3、1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
课堂小结
1、乘方的概念:求n个相同因数的积的运算叫做乘方。
2、乘方符号的确定:
an
底数
幂(乘方的结果叫做幂)
指数
an读法:a的n次方或a的n次幂
负数的奇次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都是0。
复 习
填空:
2、式子 表示的意义是_________。
1、 在 中,a叫做____,n叫做____,
乘方的结果叫做____。
底数
指数
幂
n个a相乘
3. (-4)8 __ 0 (-4)9__ 0
>
<
想一想
(1) 和 的有什
么不同?运算结果是否相同?
(2) 和 呢?
(-1)
10
8
3
(-5)
3
0.1
3
(-10)4
(-10)5
(-1)
7
练习
1、计算
(1) (2) (3) (4)
(5) (6) (7) (8)
(-1)
7
(-1)
10
8
3
(-5)
3
0.1
3
1
2
—
(- )
4
(-10)4
(-10)5
1
2
—
(- )
4
解:
=1
=-1
=512
=-125
=0.001
1
16
= —
=10000
=-100000
运用新知 体会成功:
(1)、(-5)3 (2)、
(3)、5×23 (4)、(5×2)3
(5)、(-2)2 ×(-3)2
(6)、(-2)3÷ 22
-125
256
81
40
1000
36
-2
4.计算:
先乘方、再乘除
(4)
1.先乘方、再乘除、最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
2×(-3)3-4×(-3)+15
(-2)3+(-3)×[(-4)2+2]-(-3)2÷(-2)
例3 计算
解(1)第①行数是
-2,(-2)2 ,(-2)3 ,(-2)4 , …
(2)对比①②两行中位置对应的数,你有什么发现?第②行数是第①行相应的数加2,即
-2+2,(-2)2+2,(-2)3+2,(-2)4+2,…
例4 观察下面三行数:
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
(1)第①行数按什么规律排列
(2)第②③行数与第第①行数分别有什么关系?
(3)取每行数的第10个数,计算这三个数的和。
对比①③两行中位置对应的数,你有什么发现?第③行是第①行相应的数的0.5倍,即
-2X0.5,(-2)2X0.5,(-2)3X0.5,(-2)4X0.5,…
(3)每行数中的第10个数的和是
(-2)10+[(-2)10+2]+(-2)10X0.5
=1024+(1024+2)+1024X0.5
=1024+1026+512=2562
-2,4,-8,16,-32,64,… ①
0,6,-6,18,-30,66,… ②
-1,2,-4,8,-16,32,… ③
练习
计算:
(1)(-1)10×2+(-2)3÷4
(2)
思路:先算乘方,再算乘除,再算加减
解:原式=1×2+(-8)÷4
=2+(-2)=0
思路:先算乘方,再算乘法,再算减
思路:先算括号内的运算,再从左到右
解:原式=10000+(16-12X2)
=10000-8=9992
(4)(-10)4+[(-4)2-(3+32)X2]
(3)
课堂小结
1、乘方的概念:求n个相同因数的积的运算叫做乘方。
2、乘方符号的确定:
an
底数
幂(乘方的结果叫做幂)
指数
an读法:a的n次方或a的n次幂
负数的奇次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都是0。
有理数的混合运算法则
1.先乘方、再乘除、最后加减;
2.同级运算,从左到右进行;
3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.
3.若a为任意有理数,则a2一定是( )
A.正数 B.负数
C.非负数 D.非正数
B
C
结 束 寄 语
不经历风雨,怎能见彩虹!
下 课
你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条。如图所示:
第1次
第2次
第3次
这样捏合到第 次后可拉出128根面条。
生活数学
≈
≈
异想天开
珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰。这是真的吗?
这张纸对折30次后能超过珠穆朗玛峰吗?
有一张厚度是0.1毫米的纸,将它对折1 次后,厚度为2×0.1毫米。
(1)对折2次后,厚度为多少毫米?
(2)对折30次后,厚度为多少毫米?
1次
2次
30次
如果一层楼按高3米计算,把足够长的厚0.1毫米的纸继续折叠20次约有104米高,有34层楼高;继续折叠30次后有10万多米高,有12个珠穆朗玛峰高。
分析:(1)0.1毫米×220=0.1毫米×1048576
=104.8576米
34×3=102米
(2)0.1毫米×230=0.1毫米×1073741824
=107374.1824米
8844.43 ×12=106133.16
这下你该
相信了吧!
古时候,在某个王国里有一位聪明的大臣,他发明了
国际象棋,献给了国王,国王从此迷上了下棋,为了对聪
明的大臣表示感谢,国王答应满足这个大臣的一个要求。
大臣说:“就在这个棋盘上放些米粒吧。第一格放一粒米,
第二格放两粒米,第三格放4粒米,然后是8粒米、16粒、
32粒、…一直到第64格。”“你真傻!就要这么一点米粒?”
国王哈哈大笑。大臣说:“就怕您的国库里没有这么多米!”
你认为国王的国库里有这么多米吗?
事实上,按照这个大臣的要求,放满一个棋盘上的64个格子需要1+22+23+……+263=264-1粒米。 264到底多大呢?
答案是:18 446 744 073 709 551 616
巴衣老爷说:你能每天给我10元钱,一共给我20年吗?阿凡提说:尊敬的巴衣老爷,如果你能第一天给我1毛钱,第二天给我2毛钱,第三天给我4毛钱,以此类推,一直给20天,那我就答应你的要求!巴衣老爷眼珠子一转说:那好吧!亲爱的同学们:你知道阿凡提和巴衣老爷谁得到的钱多?
