2021-2022学年北师大版九年级数学下册第3章 圆以及圆周角定理章末练习(word版、含解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册第3章 圆以及圆周角定理章末练习(word版、含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 16:26:20 | ||
图片预览

文档简介
2021-2022年北师大版九年级数学下册第3章《圆周角定理》章末精选题(附答案)
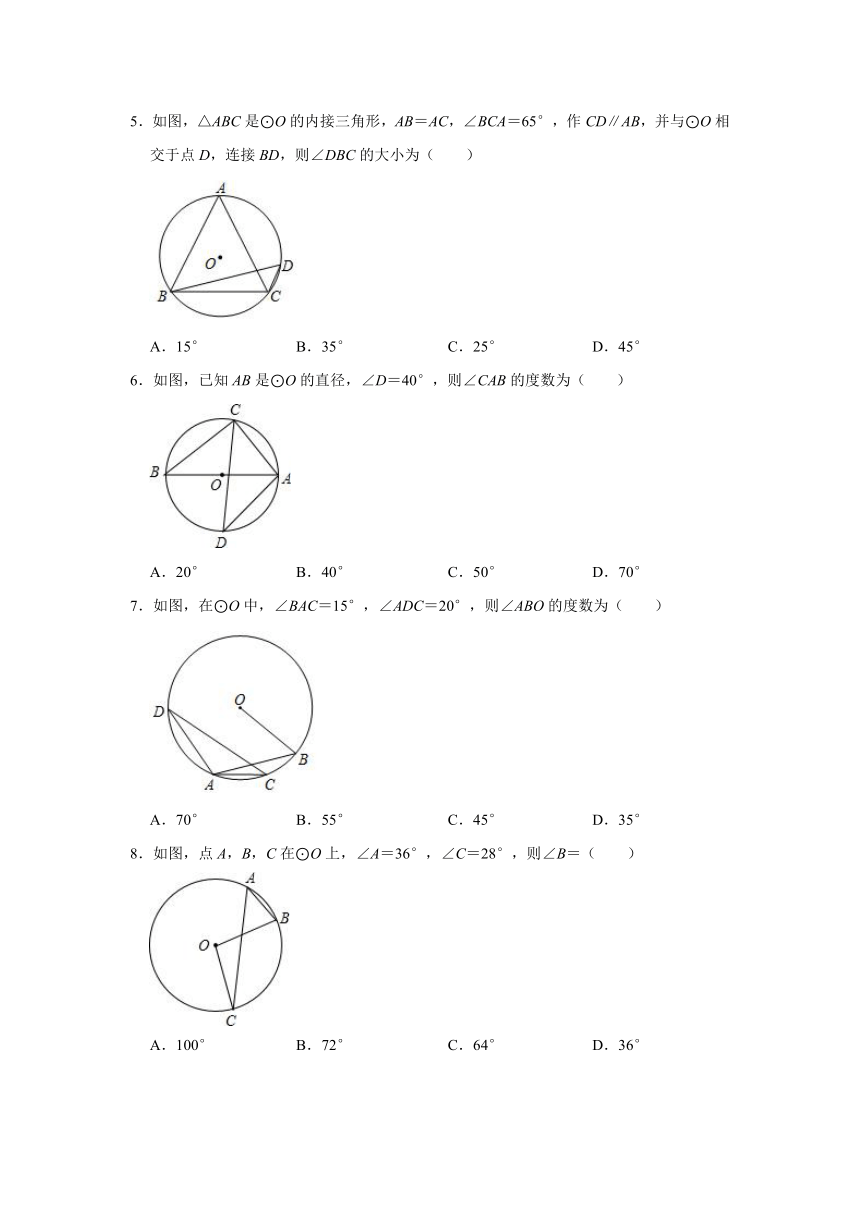
1.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
A.20° B.35° C.40° D.55°
2.如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
A.55° B.60° C.65° D.70°
3.如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
A. B. C. D.
4.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
A.100° B.110° C.115° D.120°
5.如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为( )
A.15° B.35° C.25° D.45°
6.如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
A.20° B.40° C.50° D.70°
7.如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )
A.70° B.55° C.45° D.35°
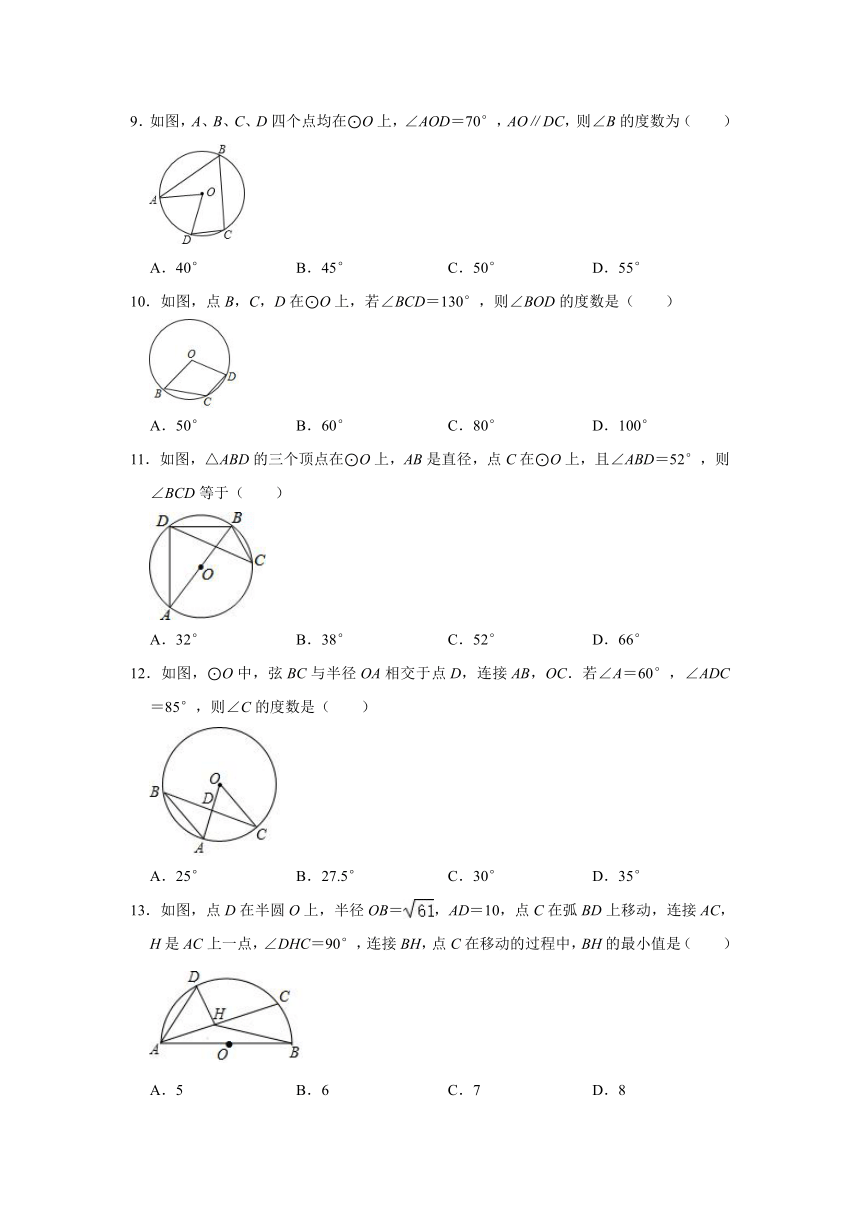
8.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
A.100° B.72° C.64° D.36°
9.如图,A、B、C、D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为( )
A.40° B.45° C.50° D.55°
10.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
11.如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于( )
A.32° B.38° C.52° D.66°
12.如图,⊙O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是( )
A.25° B.27.5° C.30° D.35°
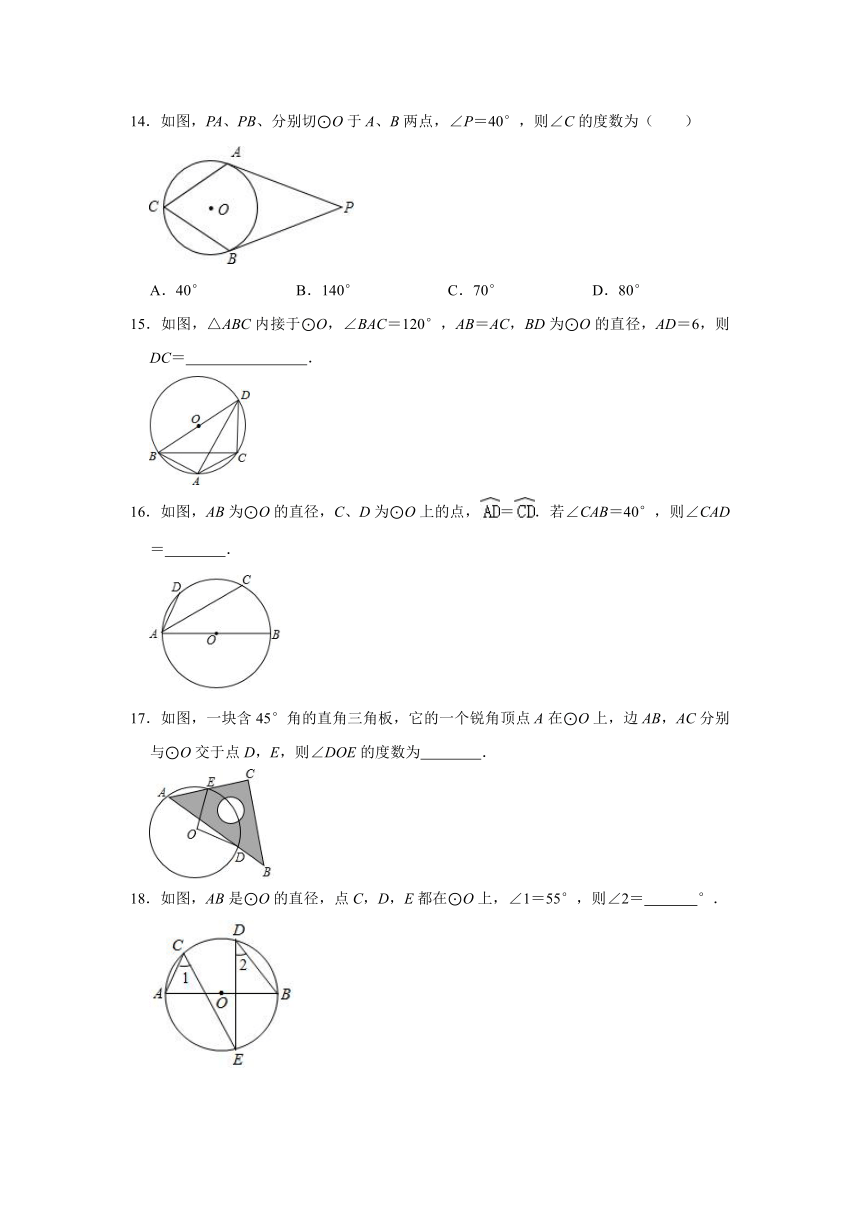
13.如图,点D在半圆O上,半径OB=,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
A.5 B.6 C.7 D.8
14.如图,PA、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A.40° B.140° C.70° D.80°
15.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= .
16.如图,AB为⊙O的直径,C、D为⊙O上的点,=.若∠CAB=40°,则∠CAD= .
17.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为 .
18.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2= °.
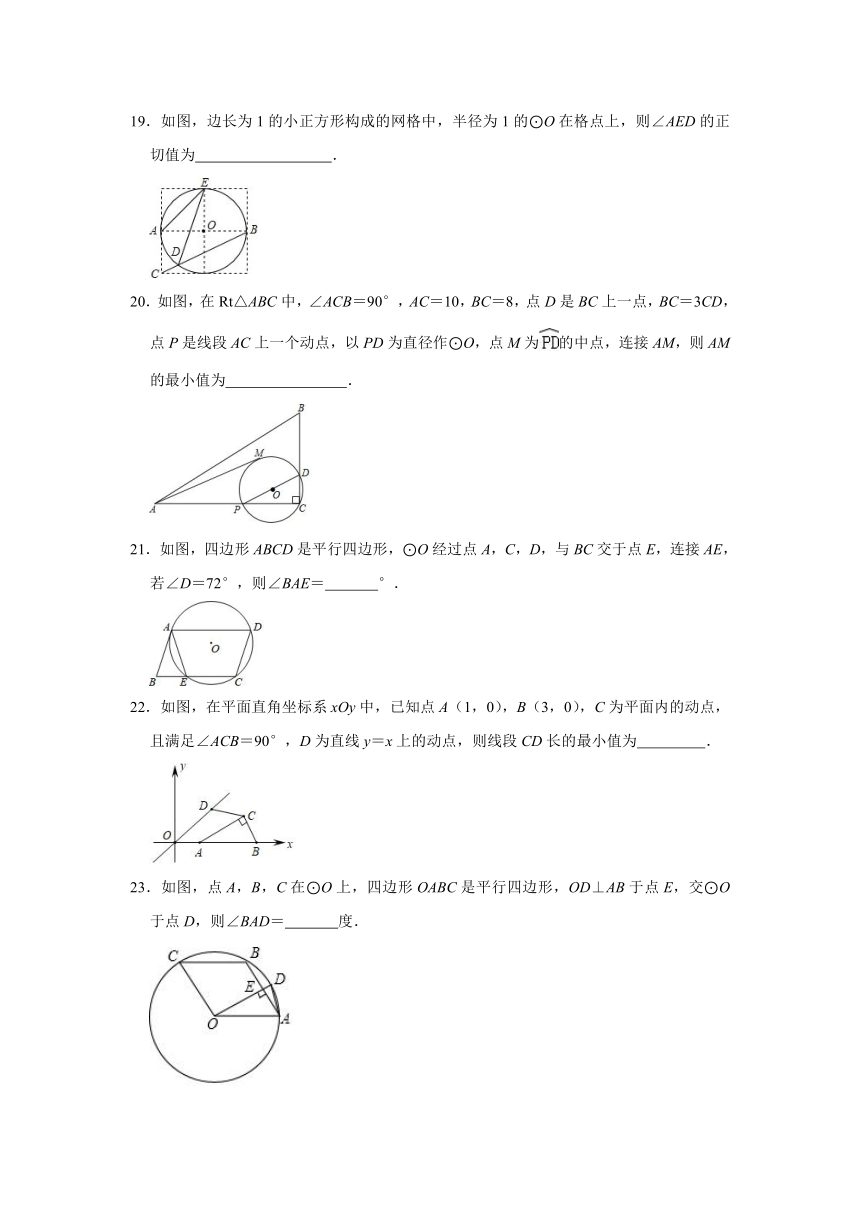
19.如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为 .
20.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM的最小值为 .
21.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=72°,则∠BAE= °.
22.如图,在平面直角坐标系xOy中,已知点A(1,0),B(3,0),C为平面内的动点,且满足∠ACB=90°,D为直线y=x上的动点,则线段CD长的最小值为 .
23.如图,点A,B,C在⊙O上,四边形OABC是平行四边形,OD⊥AB于点E,交⊙O于点D,则∠BAD= 度.
24.如图,⊙O为锐角ABC的外接圆,若∠BAO=15°,则∠C的度数为 .
25.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=50°,则∠CAD= °.
26.如图,⊙O的半径为2.弦AB=2,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是 .
27.如图,等腰直角△ABC的斜边AB下方有一动点D,∠ADB=90°,BE平分∠ABD交CD于点E,则的最小值是 .
28.如图△ABC中,∠BAC=60°,∠ABC=45°,AB=6,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,则线段EF长度最小值为 .
29.如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD= .
30.如图,⊙O的直径AB过弦CD的中点E,若∠C=26°,则∠D= .
31.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=74°,则∠BAE= °.
32.如图,已知在四边形ABCD中,∠ABC=60°,连接AC、BD交于点E,EC=2AE=4,若BE=2ED,则BD的最大值为 .
33.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
34.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为 ;
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
35.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
36.已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
37.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD=,AE=2,求⊙O的半径.
38.如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且.
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求BD的长.
39.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,连接CD;
(1)若∠CAD=23°,求∠BAC的度数;
(2)若∠ACD=45°,AC=13,求CD的长.
40.如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F.
(1)求证:=;
(2)若CE=1,EB=3,求⊙O的半径.
41.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)当DG平分∠AGC,∠ADG=45°,AF=,求弦DC的长.
参考答案
1.解:连接FB.
∵∠AOF=40°,
∴∠FOB=180°﹣40°=140°,
∴∠FEB=∠FOB=70°
∵EF=EB
∴∠EFB=∠EBF=55°,
∵FO=BO,
∴∠OFB=∠OBF=20°,
∴∠EFO=∠EBO,
∠EFO=∠EFB﹣∠OFB=35°,
故选:B.
2.解:连接OB,
∵∠ACB=25°,
∴∠AOB=2×25°=50°,
由OA=OB,
∴∠BAO=∠ABO,
∴∠BAO=(180°﹣50°)=65°.
故选:C.
3.解:过B作⊙O的直径BM,连接AM;
则有:∠MAB=∠CDB=90°,∠M=∠C;
∴∠MBA=∠CBD;
过O作OE⊥AB于E;
Rt△OEB中,BE=AB=4,OB=5;
由勾股定理,得:OE=3;
∴tan∠MBA==;
因此tan∠CBD=tan∠MBA=,故选D.
4.解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠AED=20°,
∴∠ACD=20°,
∴∠BCD=∠ACB+∠ACD=110°,
解法二:连接BE,易得∠BED为70°,再由圆内接四边形互补可得∠BCD为110°.
故选:B.
5.解:∵AB=AC、∠BCA=65°,
∴∠CBA=∠BCA=65°,∠A=50°,
∵CD∥AB,
∴∠ACD=∠A=50°,
又∵∠ABD=∠BDC=50°,
∴∠DBC=∠CBA﹣∠ABD=15°,
故选:A.
6.解:∵∠D=40°,
∴∠B=∠D=40°.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB=90°﹣40°=50°.
故选:C.
7.解:连接OA、OC,
∵∠BAC=15°,∠ADC=20°,
∴∠AOB=2(∠ADC+∠BAC)=70°,
∵OA=OB(都是半径),
∴∠ABO=∠OAB=(180°﹣∠AOB)=55°.
故选:B.
8.解:连接OA,
∵OA=OC,
∴∠OAC=∠C=28°,
∴∠OAB=64°,
∵OA=OB,
∴∠B=∠OAB=64°,
故选:C.
9.解:如图,
连接OC,
∵AO∥DC,
∴∠ODC=∠AOD=70°,
∵OD=OC,
∴∠ODC=∠OCD=70°,
∴∠COD=40°,
∴∠AOC=110°,
∴∠B=∠AOC=55°.
故选:D.
10.解:圆上取一点A,连接AB,AD,如图所示,
∵点A、B,C,D在⊙O上,∠BCD=130°,
∴∠BAD=50°,
∴∠BOD=100°,
故选:D.
11.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=52°,
∴∠A=90°﹣∠ABD=38°;
∴∠BCD=∠A=38°.
故选:B.
12.解:∵∠A=60°,∠ADC=85°,
∴∠B=85°﹣60°=25°,∠CDO=95°,
∴∠AOC=2∠B=50°,
∴∠C=180°﹣95°﹣50°=35°
故选:D.
13.解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD==12,
BM===13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
14.解:∵PA是圆的切线.
∴∠OAP=90°,
同理∠OBP=90°,
根据四边形内角和定理可得:
∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,
∴∠ACB=∠AOB=70°.
故选:C.
15.解:∵BD为⊙O的直径,
∴∠BAD=∠BCD=90°,
∵∠BAC=120°,
∴∠CAD=120°﹣90°=30°,
∴∠CBD=∠CAD=30°,
又∵∠BAC=120°,
∴∠BDC=180°﹣∠BAC=180°﹣120°=60°,
∵AB=AC,
∴∠ADB=∠ADC,
∴∠ADB=∠BDC=×60°=30°,
∵AD=6,
∴在Rt△ABD中,BD=AD÷sin60°=6÷=4,
在Rt△BCD中,DC=BD=×4=2.
故答案为:2.
16.解:如图,连接BC,BD,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=40°,
∴∠ABC=50°,
∵=,
∴∠ABD=∠CBD=∠ABC=25°,
∴∠CAD=∠CBD=25°.
故答案为:25°.
17.解:∵∠A=45°,
∴∠DOE=2∠A=90°.
故答案为:90°.
18.解:如图,连接AD.
∵AB是直径,
∴∠ADB=90°,
∵∠1=∠ADE,
∴∠1+∠2=90°,
∵∠1=55°,
∴∠2=35°,
故答案为35.
19.解:由图可得,∠AED=∠ABC,
∵⊙O在边长为1的网格格点上,
∴AB=2,AC=1,
则tan∠ABC==,
∴tan∠AED=.
故答案为:.
20.解:如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.
∵=,
∴OM⊥PD,
∴∠MOD=90°,
∴∠MCD=∠MOD=45°,
∵∠ACB=90°,
∴∠ACT=45°,
∵AT⊥CT,
∴∠ATC=90°,
∵AC=10,
∴AT=AC sin45°=5,
∵AM≥AT,
∴AM≥5,
∴AM的最小值为5,
故答案为5.
21.解:∵四边形ABCD是平行四边形,∠D=72°,
∴∠DCB=(180°﹣∠D)=108°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=72°,∠B=180°﹣∠BCD=72°
∴∠BAE=180°﹣72°﹣72°=36°,
故答案为:36
22.解:取AB的中点E,过点E作直线y=x的垂线,垂足为D,
∵点A(1,0),B (3,0),
∴OA=1,OB=3,
∴OE=2,
∴ED==,
∵∠ACB=90°,
∴点C在以AB为直径的圆上,
∴线段CD长的最小值为.
故答案为:.
23.解:∵四边形OABC是平行四边形,OC=OA,
∴OA=AB,
∵OD⊥AB,OD过O,
∴AE=BE,=,
即OA=2AE,
∴∠AOD=30°,
∴和的度数是30°
∴∠BAD=15°,
故答案为:15.
24.解:连接OB,如图,
∵OA=OB,
∴∠OBA=∠OAB=15°,
∴∠AOB=180°﹣15°﹣15°=150°,
∴∠C=∠AOB=75°.
故答案为75°.
25.解:连接OC,OD,如图所示:
∵∠CAB=50°,
∴∠COB=2∠CAB=100°.
∵=,
∴∠AOD=∠COD=(180°﹣∠COB)=40°,
∴∠CAD=∠COD=20°.
故答案为:20.
26.解:连接OA、OB,作△ABC的外接圆D,如图1,
∵OA=OB=2,AB=2,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,如图2,
当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2=,
∴△ABC的最大面积为.
故答案为:.
27.解:如图,取AB的中点O,连接OC,OD,AE.
∵∠ACB=∠ADB=90°,OA=OB,
∴OC=OD=AB,
∴A,C,B,D四点共圆,
∵CA=CB,
∴∠CBA=∠CAB=45°,
∴∠CDA=∠CBA=45°,∠CDB=∠CAB=45°,
∴∠CDB=∠CDA,
∴DE平分∠ADB,
∵BE平分∠ABD,
∴点E是△ABD的角平分线的交点,
∴AE平分∠BAD,
∴∠BAE=∠DAE,
∵∠CAE=∠CAB+∠BAE=45°+∠BAE,∠CEA=∠EDA+∠EAD=45°+∠DAE,
∴∠CAE=∠CEA,
∴CA=CE=定值,
∴当CD的值最大时,的值最小,
∴CD是直径时,的值最小,最小值==,
故答案为.
28.解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠ABC=45°,AB=6,
∴AD=BD=3,即此时圆的直径为3,
由圆周角定理可知∠EOH=∠FOH=∠BAC=60°,
∴在Rt△EOH中,EH=OE sin∠EOH=×=,
由垂径定理可知EF=2EH=,
故答案为:.
29.解:连接OD,
∵AD∥OC,
∴∠DAB=∠BOC=50°,
∵OA=OD
∴∠AOD=180°﹣2∠DAB=80°,
∴∠ACD=∠AOD=40°
故答案为40°
30.解:由圆周角的定律可知:∠D=∠ABC,
∵AB是直径,
∵E点是CD的中点,
∴∠CEB=90°,
∴∠ABC=90°﹣∠C=90°﹣26°=64°,
∴∠D=64°,
故答案为:64°
31.解:∵四边形ABCD是平行四边形,∠D=74°,
∴∠B=∠D=74°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=74°,
∴∠BAE=180°﹣74°﹣74°=32°,
故答案为:32.
32.解:如图,作△ABC的外接圆⊙O,连接OB,OA,OC,OE,过点O作OH⊥AC于H.
∵∠AOC=2∠ABC,∠ABC=60°,
∴∠AOC=120°,
∵EC=2AE=4,
∴AE=2,
∴AC=AE+EC=6,
∵OA=OC,OH⊥AC,
∴AH=HC=3,EH=AH﹣AE=1,
∵∠OAC=∠OCA=30°,
∴OH=AH tan30°=,
∴OE===2,OA=2OH=2,
∴OB=OA=2,
∵BE≤OB+OE,
∴BE≤2+2,
∴BE的最大值为2+2,
∵BE=2DE,
∴DE的最大值为1+,
∴BD的最大值为3+3.
故答案为3+3.
33.解:(Ⅰ)如图①,∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC===8.
∵AD平分∠CAB,
∴=,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5;
(Ⅱ)如图②,连接OB,OD.
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB=∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5.
34.解:(1)如图1,连接OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°﹣30°=60°,
∠E的度数为60°;
(2)①如图2,直线AD,CB交于点E,连接OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连接OD,OC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
35.(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,
在Rt△ABC中,AC2+BC2=AB2,
∴(x﹣2)2+x2=42,
解得:x1=1+,x2=1﹣(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=1+.
36.(1)证明:连接AD,
∵∠DAC=∠DEC,∠EBC=∠DEC,
∴∠DAC=∠EBC,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DCA+∠DAC=90°,
∴∠EBC+∠DCA=90°,
∴∠BGC=180°﹣(∠EBC+∠DCA)=180°﹣90°=90°,
∴AC⊥BH;
(2)解:∵∠BDA=180°﹣∠ADC=90°,∠ABC=45°,
∴∠BAD=45°,
∴BD=AD,
∵BD=8,∴AD=8,
在直角三角形ADC中,AD=8,AC=10,
根据勾股定理得:DC=6,则BC=BD+DC=14,
∵∠EBC=∠DEC,∠BCE=∠ECD,
∴△BCE∽△ECD,
∴,即CE2=BC CD=14×6=84,
∴CE==2.
37.(1)证明:如图.
∵OC=OB,
∴∠BCO=∠B.
∵∠B=∠D,
∴∠BCO=∠D;
(2)∵AB是⊙O的直径,且CD⊥AB于点E,
∴CE=CD=×4=2,
在Rt△OCE中,OC2=CE2+OE2,
设⊙O的半径为r,则OC=r,OE=OA﹣AE=r﹣2,
∴r2=(2)2+(r﹣2)2,
解得:r=3,
∴⊙O的半径为3.
38.解:(1)△ABC为等腰三角形.
理由如下:连接AE,如图,
∵,
∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵∠C+∠CAE=90°,∠ABC+∠BAE=90°,
∴∠C=∠ABC,
∴AC=AB,
∴△ABC为等腰三角形;
(2)∵△ABC为等腰三角形,AE⊥BC,
∴,
在Rt△ABE中,∵AB=10,BE=6,
∴AE===8,
∵AB为直径,
∴∠ADB=90°,
∴,
∴,
39.解:(1)∵AC⊥BD,
∴∠BEC=90°,
∵∠CAD=∠CBE=23°,
∴∠ACB=90°﹣23°=67°,
∵AB=AC,
∴∠ABC=∠ACB=67°,
∴∠BAC=180°﹣67°﹣67°=46°.
(2)∵AC⊥BD,
∴∠AEB=∠CED=90°,
∵∠ACD=∠ABD=45°,
∴△ABE,△CED都是等腰直角三角形,
∵AC=AB=13,
∴AE=AB=,
∴EC=AC﹣AE=13﹣,
∴CD=EC=13﹣13.
40.(1)证明:∵AB是圆的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AFO=∠ADB=90°,
∴OC⊥AD
∴=.
(2)解:连接AC,如图,
∵=,
∴∠CAD=∠ABC,
∵∠ECA=∠ACB,
∴△ACE∽△BCA,
∴,
∴AC2=CE CB,即AC2=1×(1+3),
∴AC=2,
∵AB是圆的直径,
∴∠ACB=90°,
∴AB===2,
∴⊙O的半径为.
41.(1)证明:如图1,连接AC,
∵AB是⊙O的直径,弦CD⊥AB,
∴=,
∴AD=AC,
∴∠ADC=∠ACD,
∵ADCG在⊙O上,
∴∠CGF=∠ADC,
∵∠AGD=∠ACD,
∴∠FGC=∠AGD;
(2)解:如图2,连接BG,AC,
∵AB是⊙O的直径,弦CD⊥AB,
∴DE=CE,
∵DG平分∠AGC,
∴∠AGD=∠CGD,
∵∠FGC=∠AGD,
∴∠AGD=∠CGD=∠FGC,
∵∠AGD+∠CGD+∠FGC=180°,
∴∠CGF=∠AGD=60°,
∴∠ADC=∠ACD=60°,
∴△ADC是等边三角形,
∵AB⊥CD,
∴∠CAE=∠DAE=30°,
∵∠ADG=45°,
∴∠CDG=∠CAG=60°﹣45°=15°,
∴∠EAF=30°+15°=45°,
Rt△AEF中,AE=EF,
∵AF=,
∴AE=EF=,
Rt△ADE中,∠DAE=30°,
∴DE=1,
∴DC=2DE=2.
1.如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
A.20° B.35° C.40° D.55°
2.如图,A,B,C是⊙O上三点,∠ACB=25°,则∠BAO的度数是( )
A.55° B.60° C.65° D.70°
3.如图,已知⊙O的半径为5,锐角△ABC内接于⊙O,BD⊥AC于点D,AB=8,则tan∠CBD的值等于( )
A. B. C. D.
4.如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为( )
A.100° B.110° C.115° D.120°
5.如图,△ABC是⊙O的内接三角形,AB=AC,∠BCA=65°,作CD∥AB,并与⊙O相交于点D,连接BD,则∠DBC的大小为( )
A.15° B.35° C.25° D.45°
6.如图,已知AB是⊙O的直径,∠D=40°,则∠CAB的度数为( )
A.20° B.40° C.50° D.70°
7.如图,在⊙O中,∠BAC=15°,∠ADC=20°,则∠ABO的度数为( )
A.70° B.55° C.45° D.35°
8.如图,点A,B,C在⊙O上,∠A=36°,∠C=28°,则∠B=( )
A.100° B.72° C.64° D.36°
9.如图,A、B、C、D四个点均在⊙O上,∠AOD=70°,AO∥DC,则∠B的度数为( )
A.40° B.45° C.50° D.55°
10.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是( )
A.50° B.60° C.80° D.100°
11.如图,△ABD的三个顶点在⊙O上,AB是直径,点C在⊙O上,且∠ABD=52°,则∠BCD等于( )
A.32° B.38° C.52° D.66°
12.如图,⊙O中,弦BC与半径OA相交于点D,连接AB,OC.若∠A=60°,∠ADC=85°,则∠C的度数是( )
A.25° B.27.5° C.30° D.35°
13.如图,点D在半圆O上,半径OB=,AD=10,点C在弧BD上移动,连接AC,H是AC上一点,∠DHC=90°,连接BH,点C在移动的过程中,BH的最小值是( )
A.5 B.6 C.7 D.8
14.如图,PA、PB、分别切⊙O于A、B两点,∠P=40°,则∠C的度数为( )
A.40° B.140° C.70° D.80°
15.如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,AD=6,则DC= .
16.如图,AB为⊙O的直径,C、D为⊙O上的点,=.若∠CAB=40°,则∠CAD= .
17.如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为 .
18.如图,AB是⊙O的直径,点C,D,E都在⊙O上,∠1=55°,则∠2= °.
19.如图,边长为1的小正方形构成的网格中,半径为1的⊙O在格点上,则∠AED的正切值为 .
20.如图,在Rt△ABC中,∠ACB=90°,AC=10,BC=8,点D是BC上一点,BC=3CD,点P是线段AC上一个动点,以PD为直径作⊙O,点M为的中点,连接AM,则AM的最小值为 .
21.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=72°,则∠BAE= °.
22.如图,在平面直角坐标系xOy中,已知点A(1,0),B(3,0),C为平面内的动点,且满足∠ACB=90°,D为直线y=x上的动点,则线段CD长的最小值为 .
23.如图,点A,B,C在⊙O上,四边形OABC是平行四边形,OD⊥AB于点E,交⊙O于点D,则∠BAD= 度.
24.如图,⊙O为锐角ABC的外接圆,若∠BAO=15°,则∠C的度数为 .
25.如图,AB为⊙O的直径,C,D为⊙O上的点,=.若∠CAB=50°,则∠CAD= °.
26.如图,⊙O的半径为2.弦AB=2,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是 .
27.如图,等腰直角△ABC的斜边AB下方有一动点D,∠ADB=90°,BE平分∠ABD交CD于点E,则的最小值是 .
28.如图△ABC中,∠BAC=60°,∠ABC=45°,AB=6,D是线段BC上的一个动点,以AD为直径作⊙O分别交AB、AC于E、F,连接EF,则线段EF长度最小值为 .
29.如图,AB为⊙O的直径,C为⊙O上一点,∠BOC=50°,AD∥OC,AD交⊙O于点D,连接AC,CD,那么∠ACD= .
30.如图,⊙O的直径AB过弦CD的中点E,若∠C=26°,则∠D= .
31.如图,四边形ABCD是平行四边形,⊙O经过点A,C,D,与BC交于点E,连接AE,若∠D=74°,则∠BAE= °.
32.如图,已知在四边形ABCD中,∠ABC=60°,连接AC、BD交于点E,EC=2AE=4,若BE=2ED,则BD的最大值为 .
33.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
34.已知:如图1,在⊙O中,直径AB=4,CD=2,直线AD,BC相交于点E.
(1)∠E的度数为 ;
(2)如图2,AB与CD交于点F,请补全图形并求∠E的度数;
(3)如图3,弦AB与弦CD不相交,求∠AEC的度数.
35.如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
36.已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧上取一点E使∠EBC=∠DEC,延长BE依次交AC于点G,交⊙O于H.
(1)求证:AC⊥BH;
(2)若∠ABC=45°,⊙O的直径等于10,BD=8,求CE的长.
37.如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.
(1)求证:∠BCO=∠D;
(2)若CD=,AE=2,求⊙O的半径.
38.如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E,且.
(1)试判断△ABC的形状,并说明理由;
(2)已知半圆的半径为5,BC=12,求BD的长.
39.如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,连接CD;
(1)若∠CAD=23°,求∠BAC的度数;
(2)若∠ACD=45°,AC=13,求CD的长.
40.如图,AB为⊙O的直径,C、D为圆上的两点,OC∥BD,弦AD与BC,OC分别交于E、F.
(1)求证:=;
(2)若CE=1,EB=3,求⊙O的半径.
41.如图,AB是⊙O的直径,弦CD⊥AB于点E,G是上一点,AG,DC的延长线交于点F.
(1)求证:∠FGC=∠AGD.
(2)当DG平分∠AGC,∠ADG=45°,AF=,求弦DC的长.
参考答案
1.解:连接FB.
∵∠AOF=40°,
∴∠FOB=180°﹣40°=140°,
∴∠FEB=∠FOB=70°
∵EF=EB
∴∠EFB=∠EBF=55°,
∵FO=BO,
∴∠OFB=∠OBF=20°,
∴∠EFO=∠EBO,
∠EFO=∠EFB﹣∠OFB=35°,
故选:B.
2.解:连接OB,
∵∠ACB=25°,
∴∠AOB=2×25°=50°,
由OA=OB,
∴∠BAO=∠ABO,
∴∠BAO=(180°﹣50°)=65°.
故选:C.
3.解:过B作⊙O的直径BM,连接AM;
则有:∠MAB=∠CDB=90°,∠M=∠C;
∴∠MBA=∠CBD;
过O作OE⊥AB于E;
Rt△OEB中,BE=AB=4,OB=5;
由勾股定理,得:OE=3;
∴tan∠MBA==;
因此tan∠CBD=tan∠MBA=,故选D.
4.解:连接AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠AED=20°,
∴∠ACD=20°,
∴∠BCD=∠ACB+∠ACD=110°,
解法二:连接BE,易得∠BED为70°,再由圆内接四边形互补可得∠BCD为110°.
故选:B.
5.解:∵AB=AC、∠BCA=65°,
∴∠CBA=∠BCA=65°,∠A=50°,
∵CD∥AB,
∴∠ACD=∠A=50°,
又∵∠ABD=∠BDC=50°,
∴∠DBC=∠CBA﹣∠ABD=15°,
故选:A.
6.解:∵∠D=40°,
∴∠B=∠D=40°.
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠CAB=90°﹣40°=50°.
故选:C.
7.解:连接OA、OC,
∵∠BAC=15°,∠ADC=20°,
∴∠AOB=2(∠ADC+∠BAC)=70°,
∵OA=OB(都是半径),
∴∠ABO=∠OAB=(180°﹣∠AOB)=55°.
故选:B.
8.解:连接OA,
∵OA=OC,
∴∠OAC=∠C=28°,
∴∠OAB=64°,
∵OA=OB,
∴∠B=∠OAB=64°,
故选:C.
9.解:如图,
连接OC,
∵AO∥DC,
∴∠ODC=∠AOD=70°,
∵OD=OC,
∴∠ODC=∠OCD=70°,
∴∠COD=40°,
∴∠AOC=110°,
∴∠B=∠AOC=55°.
故选:D.
10.解:圆上取一点A,连接AB,AD,如图所示,
∵点A、B,C,D在⊙O上,∠BCD=130°,
∴∠BAD=50°,
∴∠BOD=100°,
故选:D.
11.解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABD=52°,
∴∠A=90°﹣∠ABD=38°;
∴∠BCD=∠A=38°.
故选:B.
12.解:∵∠A=60°,∠ADC=85°,
∴∠B=85°﹣60°=25°,∠CDO=95°,
∴∠AOC=2∠B=50°,
∴∠C=180°﹣95°﹣50°=35°
故选:D.
13.解:如图,取AD的中点M,连接BD,HM,BM.
∵DH⊥AC,
∴∠AHD=90°,
∴点H在以M为圆心,MD为半径的⊙M上,
∴当M、H、B共线时,BH的值最小,
∵AB是直径,
∴∠ADB=90°,
∴BD==12,
BM===13,
∴BH的最小值为BM﹣MH=13﹣5=8.
故选:D.
14.解:∵PA是圆的切线.
∴∠OAP=90°,
同理∠OBP=90°,
根据四边形内角和定理可得:
∠AOB=360°﹣∠OAP﹣∠OBP﹣∠P=360°﹣90°﹣90°﹣40°=140°,
∴∠ACB=∠AOB=70°.
故选:C.
15.解:∵BD为⊙O的直径,
∴∠BAD=∠BCD=90°,
∵∠BAC=120°,
∴∠CAD=120°﹣90°=30°,
∴∠CBD=∠CAD=30°,
又∵∠BAC=120°,
∴∠BDC=180°﹣∠BAC=180°﹣120°=60°,
∵AB=AC,
∴∠ADB=∠ADC,
∴∠ADB=∠BDC=×60°=30°,
∵AD=6,
∴在Rt△ABD中,BD=AD÷sin60°=6÷=4,
在Rt△BCD中,DC=BD=×4=2.
故答案为:2.
16.解:如图,连接BC,BD,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠CAB=40°,
∴∠ABC=50°,
∵=,
∴∠ABD=∠CBD=∠ABC=25°,
∴∠CAD=∠CBD=25°.
故答案为:25°.
17.解:∵∠A=45°,
∴∠DOE=2∠A=90°.
故答案为:90°.
18.解:如图,连接AD.
∵AB是直径,
∴∠ADB=90°,
∵∠1=∠ADE,
∴∠1+∠2=90°,
∵∠1=55°,
∴∠2=35°,
故答案为35.
19.解:由图可得,∠AED=∠ABC,
∵⊙O在边长为1的网格格点上,
∴AB=2,AC=1,
则tan∠ABC==,
∴tan∠AED=.
故答案为:.
20.解:如图,连接OM,CM,过点A作AT⊥CM交CM的延长线于T.
∵=,
∴OM⊥PD,
∴∠MOD=90°,
∴∠MCD=∠MOD=45°,
∵∠ACB=90°,
∴∠ACT=45°,
∵AT⊥CT,
∴∠ATC=90°,
∵AC=10,
∴AT=AC sin45°=5,
∵AM≥AT,
∴AM≥5,
∴AM的最小值为5,
故答案为5.
21.解:∵四边形ABCD是平行四边形,∠D=72°,
∴∠DCB=(180°﹣∠D)=108°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=72°,∠B=180°﹣∠BCD=72°
∴∠BAE=180°﹣72°﹣72°=36°,
故答案为:36
22.解:取AB的中点E,过点E作直线y=x的垂线,垂足为D,
∵点A(1,0),B (3,0),
∴OA=1,OB=3,
∴OE=2,
∴ED==,
∵∠ACB=90°,
∴点C在以AB为直径的圆上,
∴线段CD长的最小值为.
故答案为:.
23.解:∵四边形OABC是平行四边形,OC=OA,
∴OA=AB,
∵OD⊥AB,OD过O,
∴AE=BE,=,
即OA=2AE,
∴∠AOD=30°,
∴和的度数是30°
∴∠BAD=15°,
故答案为:15.
24.解:连接OB,如图,
∵OA=OB,
∴∠OBA=∠OAB=15°,
∴∠AOB=180°﹣15°﹣15°=150°,
∴∠C=∠AOB=75°.
故答案为75°.
25.解:连接OC,OD,如图所示:
∵∠CAB=50°,
∴∠COB=2∠CAB=100°.
∵=,
∴∠AOD=∠COD=(180°﹣∠COB)=40°,
∴∠CAD=∠COD=20°.
故答案为:20.
26.解:连接OA、OB,作△ABC的外接圆D,如图1,
∵OA=OB=2,AB=2,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=2,要使△ABC的最大面积,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,如图2,
当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2=,
∴△ABC的最大面积为.
故答案为:.
27.解:如图,取AB的中点O,连接OC,OD,AE.
∵∠ACB=∠ADB=90°,OA=OB,
∴OC=OD=AB,
∴A,C,B,D四点共圆,
∵CA=CB,
∴∠CBA=∠CAB=45°,
∴∠CDA=∠CBA=45°,∠CDB=∠CAB=45°,
∴∠CDB=∠CDA,
∴DE平分∠ADB,
∵BE平分∠ABD,
∴点E是△ABD的角平分线的交点,
∴AE平分∠BAD,
∴∠BAE=∠DAE,
∵∠CAE=∠CAB+∠BAE=45°+∠BAE,∠CEA=∠EDA+∠EAD=45°+∠DAE,
∴∠CAE=∠CEA,
∴CA=CE=定值,
∴当CD的值最大时,的值最小,
∴CD是直径时,的值最小,最小值==,
故答案为.
28.解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径AD最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠ABC=45°,AB=6,
∴AD=BD=3,即此时圆的直径为3,
由圆周角定理可知∠EOH=∠FOH=∠BAC=60°,
∴在Rt△EOH中,EH=OE sin∠EOH=×=,
由垂径定理可知EF=2EH=,
故答案为:.
29.解:连接OD,
∵AD∥OC,
∴∠DAB=∠BOC=50°,
∵OA=OD
∴∠AOD=180°﹣2∠DAB=80°,
∴∠ACD=∠AOD=40°
故答案为40°
30.解:由圆周角的定律可知:∠D=∠ABC,
∵AB是直径,
∵E点是CD的中点,
∴∠CEB=90°,
∴∠ABC=90°﹣∠C=90°﹣26°=64°,
∴∠D=64°,
故答案为:64°
31.解:∵四边形ABCD是平行四边形,∠D=74°,
∴∠B=∠D=74°,
∵四边形AECD是圆内接四边形,
∴∠AEB=∠D=74°,
∴∠BAE=180°﹣74°﹣74°=32°,
故答案为:32.
32.解:如图,作△ABC的外接圆⊙O,连接OB,OA,OC,OE,过点O作OH⊥AC于H.
∵∠AOC=2∠ABC,∠ABC=60°,
∴∠AOC=120°,
∵EC=2AE=4,
∴AE=2,
∴AC=AE+EC=6,
∵OA=OC,OH⊥AC,
∴AH=HC=3,EH=AH﹣AE=1,
∵∠OAC=∠OCA=30°,
∴OH=AH tan30°=,
∴OE===2,OA=2OH=2,
∴OB=OA=2,
∵BE≤OB+OE,
∴BE≤2+2,
∴BE的最大值为2+2,
∵BE=2DE,
∴DE的最大值为1+,
∴BD的最大值为3+3.
故答案为3+3.
33.解:(Ⅰ)如图①,∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC===8.
∵AD平分∠CAB,
∴=,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5;
(Ⅱ)如图②,连接OB,OD.
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB=∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5.
34.解:(1)如图1,连接OD,OC,BD,
∵OD=OC=CD=2
∴△DOC为等边三角形,
∴∠DOC=60°
∴∠DBC=30°
∴∠EBD=30°
∵AB为直径,
∴∠ADB=90°
∴∠E=90°﹣30°=60°,
∠E的度数为60°;
(2)①如图2,直线AD,CB交于点E,连接OD,OC,AC.
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠DAC=30°,
∴∠EBD=30°,
∵AB为直径,
∴∠ACB=90°,
∴∠E=90°﹣30°=60°,
(3)如图3,连接OD,OC,
∵OD=OC=CD=2,
∴△DOC为等边三角形,
∴∠DOC=60°,
∴∠CBD=30°,
∴∠ADB=90°,
∴∠BED=60°,
∴∠AEC=60°.
35.(1)证明:∵AB为⊙O的直径,
∴∠ACB=90°,
∴AC⊥BC,
又∵DC=CB,
∴AD=AB,
∴∠B=∠D;
(2)解:设BC=x,则AC=x﹣2,
在Rt△ABC中,AC2+BC2=AB2,
∴(x﹣2)2+x2=42,
解得:x1=1+,x2=1﹣(舍去),
∵∠B=∠E,∠B=∠D,
∴∠D=∠E,
∴CD=CE,
∵CD=CB,
∴CE=CB=1+.
36.(1)证明:连接AD,
∵∠DAC=∠DEC,∠EBC=∠DEC,
∴∠DAC=∠EBC,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠DCA+∠DAC=90°,
∴∠EBC+∠DCA=90°,
∴∠BGC=180°﹣(∠EBC+∠DCA)=180°﹣90°=90°,
∴AC⊥BH;
(2)解:∵∠BDA=180°﹣∠ADC=90°,∠ABC=45°,
∴∠BAD=45°,
∴BD=AD,
∵BD=8,∴AD=8,
在直角三角形ADC中,AD=8,AC=10,
根据勾股定理得:DC=6,则BC=BD+DC=14,
∵∠EBC=∠DEC,∠BCE=∠ECD,
∴△BCE∽△ECD,
∴,即CE2=BC CD=14×6=84,
∴CE==2.
37.(1)证明:如图.
∵OC=OB,
∴∠BCO=∠B.
∵∠B=∠D,
∴∠BCO=∠D;
(2)∵AB是⊙O的直径,且CD⊥AB于点E,
∴CE=CD=×4=2,
在Rt△OCE中,OC2=CE2+OE2,
设⊙O的半径为r,则OC=r,OE=OA﹣AE=r﹣2,
∴r2=(2)2+(r﹣2)2,
解得:r=3,
∴⊙O的半径为3.
38.解:(1)△ABC为等腰三角形.
理由如下:连接AE,如图,
∵,
∴∠DAE=∠BAE,即AE平分∠BAC,
∵AB为直径,
∴∠AEB=90°,
∴AE⊥BC,
∵∠C+∠CAE=90°,∠ABC+∠BAE=90°,
∴∠C=∠ABC,
∴AC=AB,
∴△ABC为等腰三角形;
(2)∵△ABC为等腰三角形,AE⊥BC,
∴,
在Rt△ABE中,∵AB=10,BE=6,
∴AE===8,
∵AB为直径,
∴∠ADB=90°,
∴,
∴,
39.解:(1)∵AC⊥BD,
∴∠BEC=90°,
∵∠CAD=∠CBE=23°,
∴∠ACB=90°﹣23°=67°,
∵AB=AC,
∴∠ABC=∠ACB=67°,
∴∠BAC=180°﹣67°﹣67°=46°.
(2)∵AC⊥BD,
∴∠AEB=∠CED=90°,
∵∠ACD=∠ABD=45°,
∴△ABE,△CED都是等腰直角三角形,
∵AC=AB=13,
∴AE=AB=,
∴EC=AC﹣AE=13﹣,
∴CD=EC=13﹣13.
40.(1)证明:∵AB是圆的直径,
∴∠ADB=90°,
∵OC∥BD,
∴∠AFO=∠ADB=90°,
∴OC⊥AD
∴=.
(2)解:连接AC,如图,
∵=,
∴∠CAD=∠ABC,
∵∠ECA=∠ACB,
∴△ACE∽△BCA,
∴,
∴AC2=CE CB,即AC2=1×(1+3),
∴AC=2,
∵AB是圆的直径,
∴∠ACB=90°,
∴AB===2,
∴⊙O的半径为.
41.(1)证明:如图1,连接AC,
∵AB是⊙O的直径,弦CD⊥AB,
∴=,
∴AD=AC,
∴∠ADC=∠ACD,
∵ADCG在⊙O上,
∴∠CGF=∠ADC,
∵∠AGD=∠ACD,
∴∠FGC=∠AGD;
(2)解:如图2,连接BG,AC,
∵AB是⊙O的直径,弦CD⊥AB,
∴DE=CE,
∵DG平分∠AGC,
∴∠AGD=∠CGD,
∵∠FGC=∠AGD,
∴∠AGD=∠CGD=∠FGC,
∵∠AGD+∠CGD+∠FGC=180°,
∴∠CGF=∠AGD=60°,
∴∠ADC=∠ACD=60°,
∴△ADC是等边三角形,
∵AB⊥CD,
∴∠CAE=∠DAE=30°,
∵∠ADG=45°,
∴∠CDG=∠CAG=60°﹣45°=15°,
∴∠EAF=30°+15°=45°,
Rt△AEF中,AE=EF,
∵AF=,
∴AE=EF=,
Rt△ADE中,∠DAE=30°,
∴DE=1,
∴DC=2DE=2.
