4.1数列的概念(共15张PPT)
文档属性
| 名称 | 4.1数列的概念(共15张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 627.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
4.1数 列的概念
探究
知识点一 数列的概念
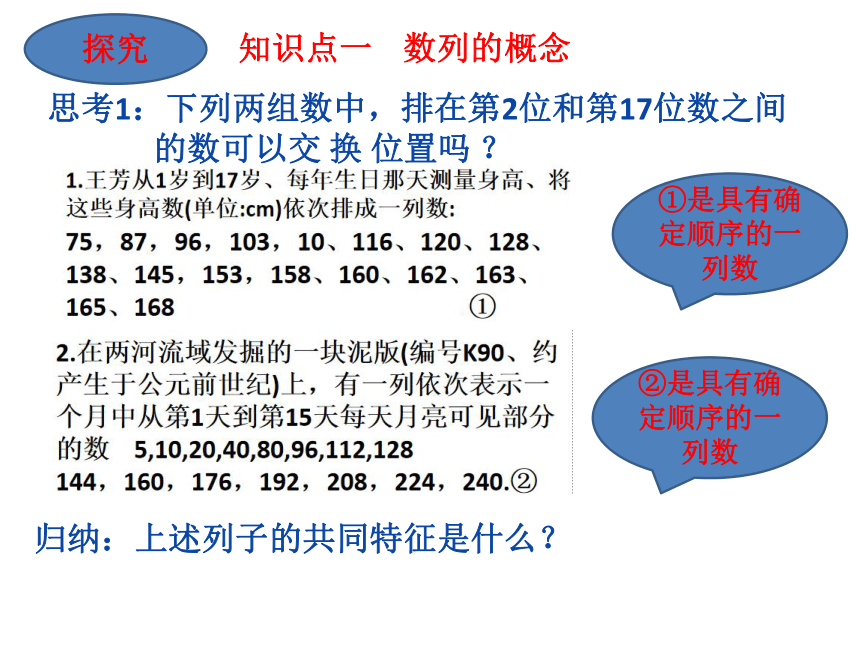
思考1:下列两组数中,排在第2位和第17位数之间
的数可以交 换 位置吗 ?
①是具有确定顺序的一列数
②是具有确定顺序的一列数
归纳:上述列子的共同特征是什么?
1.数列概念:一般地,我们把按照确定的顺序 排列的一列数称为数列( sequence of number),
2.数列的项:数列中的每一个数叫做这个数列的项.
3.第n项 :
数列的第一个位置上的数叫做这个数列的第1项,常用符号 表示,第二个位置上的数叫做这个数列的第2项,用 表示……第n个位置上的数叫做这个数列的第n项,用 表示.
4.首项 :数列的第1项也叫做首项。
知识点一
数列的概念
5. 数列的一般形式可以写成
简记为
y=f(x)
an
n
1.函数值
自变量
有穷数列 项 数 的数列.
无穷数列 项 数 的数列.
思考3:数列的实质是?与函数有什么关系?
思考2:数列按照项数如何分类?(分类一)
从函数的观点看,数列项是序号 的函数
即: 数列是从正整数集N*( 或它的有限子集)到实数集R的函数.
有限
无限
n 1 2 3 4 5 …… 14 15 16 17
75 87 96 103 110 …… 162 163 165 168
是些孤立点
有增减性
2.与函数同,也可以用表格和图像 表示:
3.与函数同,也可以定义数列的增减性:
思考4:数列按照增减性如何分类?(分类二)
递增数列 从第2项起,每一项都 它的前一项的数列 。
递减数列 从第2项起,每一项都 它的前一项的数列 。
常数列 各项都 的数列。
摆动数列 从第2项起,有些 项 它的前一项,有些 项 它的前一项的数列
大于
小于
相等
大于
小于
典型例题
数列的概念及分类
例1.下列叙述正确的是( )
A.所有数列可分为递增数列和递减数列两类
B.数列中的数由它的位置序号唯一确定
C.数列1,3,5,7可表示为{1,3,5,7}
D.同一个数在数列中不可能重复出现
B
知识点二
通项公式
如果数列 的第n项 与项数n之间的关系可以
用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
第1项
第2项
第3项
第n项
?
?
?
或
?
?
例1:根据下列数列{an}的通项公式,写出前5项,并画出它们的图象:
(1)
解:(1)当通项公式中的n=1,2,3,4,5时,数列{an}的前5项依次为1,3,6,10,15.
图象如图所示.
(2)当通项公式中的n=1,2,3,4,5时,数列{an}的前5项依次为1,0,-1,0,1.
图象如图所示.
典型例题
解:(1)这个数列的前4项的绝对值都是序号的倒数,并且奇数项为正,
偶数项为负,所以它的一个通项公式为
(2)这个数列前4项的奇数项是2,偶数项是0,所以它的一个通项公式为
典型例题
根据数列的前几项写通项公式,要注意观察项与项数的关系和相邻项间的关系.
具体可参考以下几个思路:
①先统一项的结构,如都化成分数、根式等.
②分析这一结构中变化的部分与不变的部分,探索变化部分的规律与对应序号间的函数解析式.
③对于符号正负相间的情况,可先观察其绝对值,再以(-1)n或(-1)n+1处理符号.
④对于周期出现的数列,可考虑拆成几个简单数列和的形式,或者利用周期函数,如三角函数等.
[题后感悟]
课堂小结
1.数列:按照确定的顺序排列的一列数
数列的项:首项 第n项
2.本质:从函数的观点看,数列项是序号 的函数
与函数同,也可以用表格和图像 表示--散点图。
表示方法:表格法,图像法,解析法--通项公式。
与函数同,也可以定义数列的增减性
3.分类:一、按照项数分类:
二、按照增减性分类:
4.通项公式:
如果数列{ } 的第n项 与项数n之间的关系可以
用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
课后作业
2.课本P5 练习1-3
1.上交:课本P5 练习4
3.学案完成
感谢观赏
4.1数 列的概念
探究
知识点一 数列的概念
思考1:下列两组数中,排在第2位和第17位数之间
的数可以交 换 位置吗 ?
①是具有确定顺序的一列数
②是具有确定顺序的一列数
归纳:上述列子的共同特征是什么?
1.数列概念:一般地,我们把按照确定的顺序 排列的一列数称为数列( sequence of number),
2.数列的项:数列中的每一个数叫做这个数列的项.
3.第n项 :
数列的第一个位置上的数叫做这个数列的第1项,常用符号 表示,第二个位置上的数叫做这个数列的第2项,用 表示……第n个位置上的数叫做这个数列的第n项,用 表示.
4.首项 :数列的第1项也叫做首项。
知识点一
数列的概念
5. 数列的一般形式可以写成
简记为
y=f(x)
an
n
1.函数值
自变量
有穷数列 项 数 的数列.
无穷数列 项 数 的数列.
思考3:数列的实质是?与函数有什么关系?
思考2:数列按照项数如何分类?(分类一)
从函数的观点看,数列项是序号 的函数
即: 数列是从正整数集N*( 或它的有限子集)到实数集R的函数.
有限
无限
n 1 2 3 4 5 …… 14 15 16 17
75 87 96 103 110 …… 162 163 165 168
是些孤立点
有增减性
2.与函数同,也可以用表格和图像 表示:
3.与函数同,也可以定义数列的增减性:
思考4:数列按照增减性如何分类?(分类二)
递增数列 从第2项起,每一项都 它的前一项的数列 。
递减数列 从第2项起,每一项都 它的前一项的数列 。
常数列 各项都 的数列。
摆动数列 从第2项起,有些 项 它的前一项,有些 项 它的前一项的数列
大于
小于
相等
大于
小于
典型例题
数列的概念及分类
例1.下列叙述正确的是( )
A.所有数列可分为递增数列和递减数列两类
B.数列中的数由它的位置序号唯一确定
C.数列1,3,5,7可表示为{1,3,5,7}
D.同一个数在数列中不可能重复出现
B
知识点二
通项公式
如果数列 的第n项 与项数n之间的关系可以
用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
第1项
第2项
第3项
第n项
?
?
?
或
?
?
例1:根据下列数列{an}的通项公式,写出前5项,并画出它们的图象:
(1)
解:(1)当通项公式中的n=1,2,3,4,5时,数列{an}的前5项依次为1,3,6,10,15.
图象如图所示.
(2)当通项公式中的n=1,2,3,4,5时,数列{an}的前5项依次为1,0,-1,0,1.
图象如图所示.
典型例题
解:(1)这个数列的前4项的绝对值都是序号的倒数,并且奇数项为正,
偶数项为负,所以它的一个通项公式为
(2)这个数列前4项的奇数项是2,偶数项是0,所以它的一个通项公式为
典型例题
根据数列的前几项写通项公式,要注意观察项与项数的关系和相邻项间的关系.
具体可参考以下几个思路:
①先统一项的结构,如都化成分数、根式等.
②分析这一结构中变化的部分与不变的部分,探索变化部分的规律与对应序号间的函数解析式.
③对于符号正负相间的情况,可先观察其绝对值,再以(-1)n或(-1)n+1处理符号.
④对于周期出现的数列,可考虑拆成几个简单数列和的形式,或者利用周期函数,如三角函数等.
[题后感悟]
课堂小结
1.数列:按照确定的顺序排列的一列数
数列的项:首项 第n项
2.本质:从函数的观点看,数列项是序号 的函数
与函数同,也可以用表格和图像 表示--散点图。
表示方法:表格法,图像法,解析法--通项公式。
与函数同,也可以定义数列的增减性
3.分类:一、按照项数分类:
二、按照增减性分类:
4.通项公式:
如果数列{ } 的第n项 与项数n之间的关系可以
用一个公式来表示,那么这个公式就叫做这个数列的通项公式。
课后作业
2.课本P5 练习1-3
1.上交:课本P5 练习4
3.学案完成
感谢观赏
