八年级上册数学12章轴对称教学案
文档属性
| 名称 | 八年级上册数学12章轴对称教学案 |  | |
| 格式 | zip | ||
| 文件大小 | 644.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-16 13:35:20 | ||
图片预览




文档简介
课 题 12.1 轴对称 课型 新授 课时编号
学习目标 知识与技能:生活实例中认识轴对称图.分析轴对称图形,理解轴对称的概念. 过程与方法: 通过丰富的生活实例认识轴对称,能够识别简单的轴对称图形及其对称轴. 情感态度与价值观: 通过丰富的生活实例认识轴对称,培养学生对美的感受。
学习重难点 教学重点 轴对称图形的概念. 教学难点 能够识别轴对称图形并找出它的对称轴.
集 体 备 课 个 性 设 计
我们生活在一个充满对称的世界中,许多建筑物都设计成对称形,艺术作品的创作往往也从对称角度考虑,自然界的许多动植物也按对称形生长,中国的方块字中些也具有对称性……对称给我们带来多少美的感受!初步掌握对称的奥秒,不仅可以帮助我们发现一些图形的特征,还可以使我们感受到自然界的美与和谐.
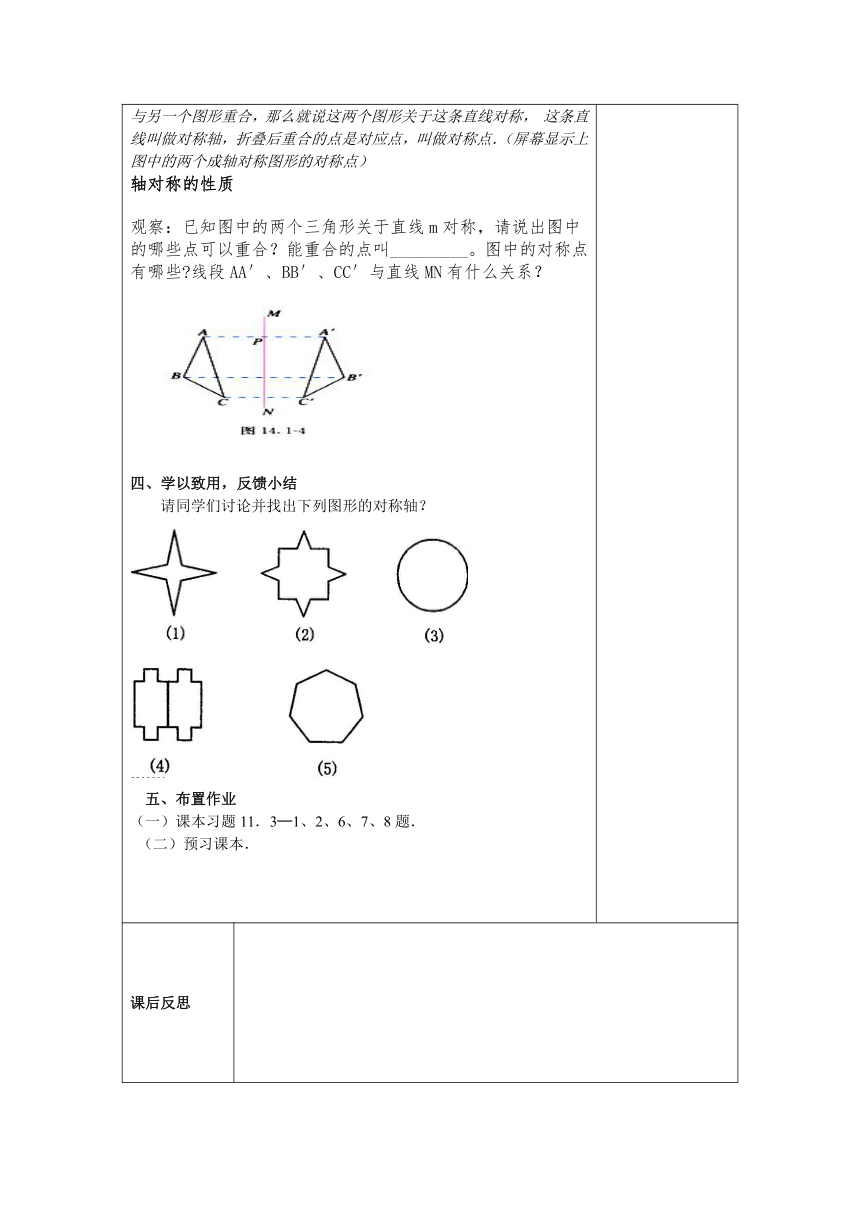
轴对称是对称中重要的一种,让我们一起走进轴对称世界,探索它的秘密吧!从这节课开始,我们来学习第十四章:轴对称.今天我们来研究第一节,认识什么是轴对称图形,什么是对称轴.二、自主学习、合作探究(一)同学们先看课本内容,并完成俩列问题:什么是轴对称图形?2、什么是对称轴?(二)活动一观察:我们先来看几幅图片(课件出示图片),观察它们都有些什么共同特征.(同学们先观察,共同讨论回答)(三)活动二做一做:同学们将准备好的一张纸对折后,用笔沿着折线画一条直线,然后从折叠处剪出一个你喜欢的图形,想一想,展开后会是一个什么样的图形?[教学说明:让同学们从动手实践中总结出结论:剪出来的图形关于折线对称] (演示多媒体课件)三、点拨释疑如果一个图形沿一直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线(成轴)对称对称轴:接下来我们来探讨一个有关对称轴的问题.有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条,请完成下列问题.你能找出它们的对称轴吗?分小组讨论,并画出来. (点击课件进行演示)刚才我们研究了一个图形具有轴对称的特征,你想不想看看两个图形是否也具有这样的特征呢?(屏幕显示)结论:像这样,把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.(屏幕显示上图中的两个成轴对称图形的对称点)轴对称的性质观察:已知图中的两个三角形关于直线m对称,请说出图中的哪些点可以重合?能重合的点叫_________。图中的对称点有哪些 线段AA′、BB′、CC′与直线MN有什么关系?四、学以致用,反馈小结请同学们讨论并找出下列图形的对称轴? 五、布置作业(一)课本习题11.3─1、2、6、7、8题. (二)预习课本.
课后反思
课 题 12.2作轴对称图形 课型 新授 课时编号
学习目标 能够按要求作出简单平面图形经过轴对称后的图形.
学习重难点 教学重点: 能够按要求作出简单平面图形经过轴对称后的图形.教学难点: 应用轴对称解决实际问题.
集 体 备 课 个 性 设 计
一.提出问题,创设情境 上节课我们学习了轴对称图形的概念,知道了一个图形经过轴对称变换可以得到它的轴对称图形,那么具体过程如何操作呢?这就是我们这节课要学习的.下面同学们来欣赏许多漂亮的图案. 总结:你看到的美丽的图案有什么特点 他们的另一半是怎么得到的 二.导入新课:我们今天就来学习作出简单平面图形经过轴对称后的图形.三.探究新知识: 如何作一个图形经过轴对称后的图形呢?探究(1)探索活动(一): 1. 你能否根据左手掌印画出右手掌印?(注意对称轴的选取) 2. 书39页几个图案是怎样得到的? 3 (课件演示:如何找对称轴?)通过以上探索(1),你有什么收获 小组交流后加以总结:1.对称轴的方向和位置发生变化时,得到的图形的方向和位置也发生变化。2.由一个图形可以得到它关于对称轴的对称图形,这两个图形的形状大于完全相同(对称点对称轴)3.新图形上的每一点,都是原图形上的某一点关于直线L的对称点;4连接任意一对对应点的线段被对称轴垂直平分。探究活动(2)如果有一个图形和一条直线,如何作出这个图形关于这条直线的对称图形呢?我们知道:任何一个图形都是由点组成的.因为我们来作一个点关于一条直线的对称点.由已经学过的知识知道:对应点的连线被对称轴垂直平分.所以,已知对称轴L和一个点A,要画出点 关于L的对应点A′,可采取如下方法: (1)过点A作对称轴L的垂线,垂足为B; (2)在垂线上截取BA′,使BA′=AB. 点A′就是点A关于直线L的对应点. 好,大家来动手画一点A关于直线L对称的对应点。 做一做:如下图,已知点A和直线L,试画出点A关于直线L的对称点A'。 …… 例题:已知△ABC,直线L,画出△ABC关于直线L对称的图形。 同学们小组讨论一下:仿照以上的探索,怎样才能更好的作出三角形的对 称三角形呢?(演示课件) 下面大家一起动手做. 作法:如图(2). (1)过点A作直线L的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线L的对称点; (2)类似地,作出点B、C关于直线L的对称点B′、C′; (3)连结A′B′、B′C′、C′A′,得到△A′B′C′即为所求.五. 课堂总结: 1、通过今天的学习,大家有何收获?2. 还有哪些疑难问题需要帮助 六.布置作业:1.课本41页练习中的1 2
课后反思
课 题 等腰三角形 课型 新授 课时编号
学习目标 经历剪纸、折纸等活动,进一步认识等腰三角形,了解等腰三角形是轴对称图形.
学习重难点 重点:等腰三角形的性质的探索和应用.难点:等腰三角形的性质的证明.
集 体 备 课 个 性 设 计
一、创设情境在前面的学习中,我们认识了轴对称图形,探究了轴对称的性质,并且能够作出一个简单平面图形关于某一直线的轴对称图形,还能够通过轴对称变换来设计一些美丽的图案.这节课我们就是从轴对称的角度来认识一些我们熟悉的几何图形.来研究:①三角形是轴对称图形吗?②什么样的三角形是轴对称图形?二、探究新知师生拿出课先准备好的长方形的纸片,按教科书第140页的要求剪出△ABC.设问1:△ABC有什么特点 设问2:△ABC是轴对称图形吗 它的对称轴是什么 学生思考、回顾剪纸过程,把等腰三角形ABC沿折痕对折,容易回答△ABC是轴对称图形,折痕AD所在的直线是它的对称轴.设问3:你还发现了什么现象,继而猜想等腰三角形ABC有哪些性质 学生讨论、汇报:①∠B=∠C →两个底角相等②BD=CD →AD为底边BC上的中线③∠BAD=∠CAD →AD为顶角∠BAC的平分线∠ADB=∠ADC=90° →AD为底边BC上的高 用语言叙述为:性质1 等腰三角形的两个底角相等(简写成“等边对等角”);性质2 等腰三角形的顶角平分线、底边上的中线;底边上的高互相重合.(可简记为“三线合一”性质)设问4:你能用所学的知识验证等腰三角形的性质吗 1.证明等腰三角形底角的性质. 教师要求学生根据猜想的结论画出相应的图形,写出已知和求证.已知:如图1,在△ABC中,AB=AC 求证:∠B=∠C. 师生共同分析证明思路并证明.强调以下两点: (1)利用三角形全等来证明两角相等. 为证∠B=∠C,需证明以∠B,∠C为元素的两个三角形全等,需要添加辅助线构造符合证明要求的两个三角形. (2)添加辅助线的方法可以多样. 例如,常见的作顶角∠BAC的平分线,或作底边BC上的中线或作底边BC上的高等.让学生选择一种辅助线完成证明过程.2.证明等腰三角形的“三线合一”性质.鼓励学生用多种方法证明. 三、学以致用1,已知等腰三角形的一个底角是36°,则其余两角为______ 2,已知等腰三角形一个角是36°,则其余两角为______ 3,已知等腰三角形一个角是110°,则其余两角为______。 四、知识小结1、等腰三角形是轴对称图形; 2、等边对等角的性质;六、作业布置1.必做题:教科书第143页练习1、2、3.2.选做题:教科书第150页习题12.3第8题.
课后反思
课 题 等腰三角形 课型 新授 课时编号
学习目标 通过性质定理和推论运用进一步培养学生分析问题解决问题的能力,渗透转化思想.
学习重难点 重点:等腰三角形性质的应用.难点:添加合适的辅助线.
集 体 备 课 个 性 设 计
一、知识回顾1.等腰三角形的性质定理是什么? 2.等腰三角形一个角为50°,求其它两角.3.等腰三角形一个外角为70°,求三个内角的度数.二、探究新知例1 如图所示已知:△ABC中,AB=AC,点D在AC上,且BD=BC=AD.求:△ABC各角的度数.例2 如图所示,已知:点D、E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE.讨论:(1)等腰三角形底边中点到两腰的距离相等吗?(2)利用类似的方法,还可以得到等腰三角形中哪些线段相等?三、学以致用1.如图所示,已知:AB=AE,BC=ED,∠B=∠E,AM⊥CD.求证:CM=MD.2.如图所示,已知:△ABC和△EBD均为等边三角形,点D在BC上.求证:AD=CE.四、知识小结列方程解几何计算题是几何中常用的方法,要善于将几何的定理、等式转化为代数方程.(2)等腰三角形中常添的辅助线是顶角平分线或底边上的中线和高线.(3)要灵活运用等腰三角形的性质. 五、诊断检测(一)1.等腰△ABC的底角是60°,则顶角是________度.2.等腰三角形“三线合一”是指___________.3.等腰三角形的顶角是n°,则两个底角的角平分线所夹的钝角是_________.4.如图,△ABC中AB=AC,EB=BD=DC=CF,∠A=40°,则∠EDF的度数是_____.5.△ABC中,AB=AC.点D在BC边上 (1)∵AD平分∠BAC,∴_______=________;________⊥_________; (2)∵AD是中线,∴∠________=∠________;________⊥________; (3)∵AD⊥BC,∴∠________=∠_______;_______=_______.六、作业布置如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC交AB于E,求证:AE=BE.
课后反思
课 题 等腰三角形 课型 新授 课时编号
学习目标 ①会阐述、推证等腰三角形的判定定理.②学会比较等腰三角形性质定理和判定定理的联系与区别.
学习重难点 重点:等腰三角形的判定定理的探索和应用.难点:等腰三角形的判定与性质的区别.
集 体 备 课 个 性 设 计
一、知识回顾等腰三角形的性质有哪些?1:等腰三角形的两底角相等.2:等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.二、探究新知(一)思考:如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)? 在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系? 即:如果一个三角形有两个角相等,那么这个三角形所对的两条边也相等. 如何验证 学生根据命题画出图形,并写出已知、求证.已知:如图,在△ABC中,∠B=∠C.求证:AB=AC学生寻求证明途径.证明:作AD⊥BC,垂足为D,在⊿ABD和⊿ACD中,作∠BAC的平分线AD.在△BAD和△CAD中∴⊿ABD≌ ⊿ACD∴AB=AC[例2]求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.分析:这个题是文字叙述的证明题,我们首先得将文字语言转化成相应的数学语言,再根据题意画出相应的几何图形.已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC(如图). 求证:AB=AC.三、学以致用(一)1、如图,∠A=360,∠DBC=360,∠C=720,分别计算∠1、 ∠2的度数。2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?3、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。四、知识小结1.通过这两节课的学习,你学会了几种判断等腰三角形的方法 2.你会比较等腰三角形性质定理与判定定理的联系与区别吗 六、作业布置1.必做题:教科书第145页练习1、2、3.2.选做题:教科书第150页习题12.3第9、10题.
课后反思
课 题 等边三角形 课型 新授 课时编号
学习目标 经历画、折等实践操作活动过程,发展学生的空间观念,,并培养学生的动手实践能力。
学习重难点 重点:等边三角形的性质和判定方法. 难点:等边三角形性质的应用.
集 体 备 课 个 性 设 计
一.欣赏图片,感受生活通过欣赏我发现了 二.小组合作,探究新知(一)1.观察老师给你的等边三角形纸片, 根据等腰三角形的性质,猜想等边三角形有哪些性质?并通过测量、折纸、证明等方式进行验证。探究得出以下性质: (1). (2). (3). (4). 小组合作,探究新知(二)1.等边三角形的三个角都相等,并且每个角都是60°,反之,如果我告诉你一个三角形三个角都相等,你能确定这是等边三角形吗?理由呢?得出结论:(1). 理由: 2.实践应用 如图,课外兴趣小组在一次测量活动中,测得∠APB=60°, AP=BP=200m,他们便得出了一个结论:池塘最长处不小于200m.他们的结论对吗 解:∵AP=BP, ∠APB=60° ∴∠ =∠ = ∴ ∠ = ∠ =∠ 从而△APB是 ,AB的长是 m,由此可以得出兴趣小组的结论是 的。3. .你认为有一个角等于60°的等腰三角形是等边三角形吗? 结论: 三、学以致用1.等边三角形的 相等, 相等。2. △ABC为等边三角形,BD为高,CE为角平分线,BD与CE相交于点O,则,∠ABD= ,∠BOC= .3.等边三角形的对称轴有( ) (A)1条(B)2条(C)3条(D)4条4.下列四个说法中,不正确的有( )(1)三条边都相等的三角形是等边三角形。(2)有两个角等于60°的三角形是等边三角形。(3)有一个是60°的等腰三角形是等边三角形。 (4)等腰三角形是等边三角形。(A)0个(B)1个(C)2个(D)3个5.如图,在等边三角形ABC中,AD是BC上的高,且∠BDE=∠CDF=60°,图中与BD相等的线段有 。四、动手操作,感悟新知在等边三角形ABC的边AB,AC上分别截取 AD=AE△ADE是等边三角形吗?试说明理由。五、拓展思维1.比一比,看谁最聪明如图,是用6根火柴搭建的等边三角形,再给你几根火柴可摆出4个等边三角形?摆一摆,并在右图中画出来。六、走进中考,1.如图,A,B,C三座 城市在一条直线上,A,B,D 三座城市之间距离相等,A,C,E三座城市之间距离也相等.已有公路AB,AD,BD,AC,AE,EC六条,根据经济发展需要,要再建设两条高速公路BE,CD,猜猜BE,CD长度之间有什么关系 七.知识小结等边三角形与等腰三角形在定义,性质和判定的异同
课后反思
课 题 等边三角形 课型 新授 课时编号
学习目标 1.探索──发现──猜想──证明直角三角形中有一个角为30°的性质.2.有一个角为30°的直角三角形的性质的简单应用.
学习重难点 含30°角的直角三角形性质定理的探索与证明.
集 体 备 课 个 性 设 计
一.复习旧知1、等边三角形三边 ,三个角都等于 度.2、等边三角形是轴对称图形,有 条对称轴. 3、 的等腰三角形是等边三角形4。如图,已知△ABC和△BDE都是等边三角形, 求证:AE=CD二.问题情境, 问题:用两个全等的含30°角的直角三角尺,你能拼出一个怎样的三角形?能拼出一个等边三角形吗?说说你的理由. 由此你能想到,在直角三角形中,30°角所对的直角边与斜边有怎样的大小关系?你能证明你的结论吗? 三.动手动脑 我摆出了如下两个三角形 已知:如图,在Rt△ABC中,∠C=90°,∠BAC=30°.求证:BC=AB. 四.小试牛刀1。如图,△ABC中,若AC⊥BC,∠BAC=30°,则∠B=_____°,延长BC到D使BD=AB,连结AD,则△ABD是_____三角形,BC=_____=_____。 2。如图,∠C=90°,D是CA的延长线上一点, ∠BDC=15 °,且AD=AB,则BC= AD3. 如图,在△ABC中, AB=AC=2a且∠ABC=∠ACB=150,CD是腰AB上的高,求CD的长 五.能力提高1。如图,在△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=14.4cm,则AD= 2.如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BD、DE要多长? 六.总结反思通过这节课的学习,我学到了:
课后反思
课 题 《轴对称》小结 课型 复习 课时编号
学习目标 学生对整章的学习内容做一回顾,系统地把握全章的知识要点和基本技能
学习重难点 教学重点:判断图形是否是轴对称图形教学难点: 灵活运用上述性质解决问题、轴对称图案的设计
集 体 备 课 个 性 设 计
<一> 知识回顾问题1:轴对称图形的定义是什么 它是判断图形是否是轴对称图形的依据。问题2:是否会画轴对称图形的对称轴 找出轴对称图形的任一组对称点,连结对称点,画对称点所连线段的垂直平分线,即得到该图形对称轴。问题3:轴对称图形对称点的连线与对称轴有什么关系 轴对称图形对称点的连线被对称轴垂直平分。问题4:线段垂直平分线、角平分线具有什么性质 线段垂直平分线上的点到线段两端的距离相等;角平分线上的点到角两边的距离相等。问题5:等腰三角形有什么性质 等腰三角形底边的中线、高线、顶角的平分线互相重合,等腰三角形的两个底角相等(等边对等角),等边三角形的三个角都等于60°。问题6:如何判断三角形是等腰三角形 等边三角形 如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边);有两个角是60°的三角形是等边三角形,有一个角是60°的等腰三角形是等边三角形。<三> 例题 基础知识: 1.下列图案是轴对称图形的有( ) A.1个 B.2个 C.3个 D.4个2.如右图所示,下列图形中,一定是轴对称图形的有( )个。线段、三角形、平行四边形、梯形,半圆3.观察下面的英文字母,其中是轴对称图形的有( )个。A,C,D,E,F,H,J,S,M,Y,Z4. 等腰三角形的一个内角是700,则它的另外两个角的度数分别( )。5. 已知1,3,x分别为等腰△ABC的三边长,化简( )6. 等腰三角形的一个外角是40度,则这个等腰三角形的底角等于( )度。7.如图,三角形ABC中,AB=AC,∠A=40度,AB的垂直平分线MN交AC于D,连接BD,∠DBC等于( )度知识拓展:1.如图,△ABC中,∠ABC=1200,AM=AN,CN=CP, 求 ∠MNP的度数.2. 已知AD是等腰三角形一腰上的高,∠DAB=600,求△ABC的三个内角的度数。3如图,△ABC中,AD平分∠CAB交BC于D,且CD=2,∠C=900,∠DEF=900,∠B=∠FDB=22.50,AE=6,DF=4,求AB的长. 4 如图,△ABC中,AB=AC,E 在CA的延长线上,∠AEF=∠AFE,求证:EF⊥BC<四> 课堂小结: 通过本节课复习,同学们应掌握本章知识和技能,并运用所学知识和技能解决问题
课后反思
E
B
A
D
C
F
∠ABC=∠ACB
∠ADB=∠ADC=90度
AD=AD
∵
_
A
_
C
_
B
A
B
C
D
E
O
_
C
_
A
_
B
·
A
B
C
学习目标 知识与技能:生活实例中认识轴对称图.分析轴对称图形,理解轴对称的概念. 过程与方法: 通过丰富的生活实例认识轴对称,能够识别简单的轴对称图形及其对称轴. 情感态度与价值观: 通过丰富的生活实例认识轴对称,培养学生对美的感受。
学习重难点 教学重点 轴对称图形的概念. 教学难点 能够识别轴对称图形并找出它的对称轴.
集 体 备 课 个 性 设 计
我们生活在一个充满对称的世界中,许多建筑物都设计成对称形,艺术作品的创作往往也从对称角度考虑,自然界的许多动植物也按对称形生长,中国的方块字中些也具有对称性……对称给我们带来多少美的感受!初步掌握对称的奥秒,不仅可以帮助我们发现一些图形的特征,还可以使我们感受到自然界的美与和谐.
轴对称是对称中重要的一种,让我们一起走进轴对称世界,探索它的秘密吧!从这节课开始,我们来学习第十四章:轴对称.今天我们来研究第一节,认识什么是轴对称图形,什么是对称轴.二、自主学习、合作探究(一)同学们先看课本内容,并完成俩列问题:什么是轴对称图形?2、什么是对称轴?(二)活动一观察:我们先来看几幅图片(课件出示图片),观察它们都有些什么共同特征.(同学们先观察,共同讨论回答)(三)活动二做一做:同学们将准备好的一张纸对折后,用笔沿着折线画一条直线,然后从折叠处剪出一个你喜欢的图形,想一想,展开后会是一个什么样的图形?[教学说明:让同学们从动手实践中总结出结论:剪出来的图形关于折线对称] (演示多媒体课件)三、点拨释疑如果一个图形沿一直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.这时,我们也说这个图形关于这条直线(成轴)对称对称轴:接下来我们来探讨一个有关对称轴的问题.有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条,请完成下列问题.你能找出它们的对称轴吗?分小组讨论,并画出来. (点击课件进行演示)刚才我们研究了一个图形具有轴对称的特征,你想不想看看两个图形是否也具有这样的特征呢?(屏幕显示)结论:像这样,把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴,折叠后重合的点是对应点,叫做对称点.(屏幕显示上图中的两个成轴对称图形的对称点)轴对称的性质观察:已知图中的两个三角形关于直线m对称,请说出图中的哪些点可以重合?能重合的点叫_________。图中的对称点有哪些 线段AA′、BB′、CC′与直线MN有什么关系?四、学以致用,反馈小结请同学们讨论并找出下列图形的对称轴? 五、布置作业(一)课本习题11.3─1、2、6、7、8题. (二)预习课本.
课后反思
课 题 12.2作轴对称图形 课型 新授 课时编号
学习目标 能够按要求作出简单平面图形经过轴对称后的图形.
学习重难点 教学重点: 能够按要求作出简单平面图形经过轴对称后的图形.教学难点: 应用轴对称解决实际问题.
集 体 备 课 个 性 设 计
一.提出问题,创设情境 上节课我们学习了轴对称图形的概念,知道了一个图形经过轴对称变换可以得到它的轴对称图形,那么具体过程如何操作呢?这就是我们这节课要学习的.下面同学们来欣赏许多漂亮的图案. 总结:你看到的美丽的图案有什么特点 他们的另一半是怎么得到的 二.导入新课:我们今天就来学习作出简单平面图形经过轴对称后的图形.三.探究新知识: 如何作一个图形经过轴对称后的图形呢?探究(1)探索活动(一): 1. 你能否根据左手掌印画出右手掌印?(注意对称轴的选取) 2. 书39页几个图案是怎样得到的? 3 (课件演示:如何找对称轴?)通过以上探索(1),你有什么收获 小组交流后加以总结:1.对称轴的方向和位置发生变化时,得到的图形的方向和位置也发生变化。2.由一个图形可以得到它关于对称轴的对称图形,这两个图形的形状大于完全相同(对称点对称轴)3.新图形上的每一点,都是原图形上的某一点关于直线L的对称点;4连接任意一对对应点的线段被对称轴垂直平分。探究活动(2)如果有一个图形和一条直线,如何作出这个图形关于这条直线的对称图形呢?我们知道:任何一个图形都是由点组成的.因为我们来作一个点关于一条直线的对称点.由已经学过的知识知道:对应点的连线被对称轴垂直平分.所以,已知对称轴L和一个点A,要画出点 关于L的对应点A′,可采取如下方法: (1)过点A作对称轴L的垂线,垂足为B; (2)在垂线上截取BA′,使BA′=AB. 点A′就是点A关于直线L的对应点. 好,大家来动手画一点A关于直线L对称的对应点。 做一做:如下图,已知点A和直线L,试画出点A关于直线L的对称点A'。 …… 例题:已知△ABC,直线L,画出△ABC关于直线L对称的图形。 同学们小组讨论一下:仿照以上的探索,怎样才能更好的作出三角形的对 称三角形呢?(演示课件) 下面大家一起动手做. 作法:如图(2). (1)过点A作直线L的垂线,垂足为点O,在垂线上截取OA′=OA,点A′就是点A关于直线L的对称点; (2)类似地,作出点B、C关于直线L的对称点B′、C′; (3)连结A′B′、B′C′、C′A′,得到△A′B′C′即为所求.五. 课堂总结: 1、通过今天的学习,大家有何收获?2. 还有哪些疑难问题需要帮助 六.布置作业:1.课本41页练习中的1 2
课后反思
课 题 等腰三角形 课型 新授 课时编号
学习目标 经历剪纸、折纸等活动,进一步认识等腰三角形,了解等腰三角形是轴对称图形.
学习重难点 重点:等腰三角形的性质的探索和应用.难点:等腰三角形的性质的证明.
集 体 备 课 个 性 设 计
一、创设情境在前面的学习中,我们认识了轴对称图形,探究了轴对称的性质,并且能够作出一个简单平面图形关于某一直线的轴对称图形,还能够通过轴对称变换来设计一些美丽的图案.这节课我们就是从轴对称的角度来认识一些我们熟悉的几何图形.来研究:①三角形是轴对称图形吗?②什么样的三角形是轴对称图形?二、探究新知师生拿出课先准备好的长方形的纸片,按教科书第140页的要求剪出△ABC.设问1:△ABC有什么特点 设问2:△ABC是轴对称图形吗 它的对称轴是什么 学生思考、回顾剪纸过程,把等腰三角形ABC沿折痕对折,容易回答△ABC是轴对称图形,折痕AD所在的直线是它的对称轴.设问3:你还发现了什么现象,继而猜想等腰三角形ABC有哪些性质 学生讨论、汇报:①∠B=∠C →两个底角相等②BD=CD →AD为底边BC上的中线③∠BAD=∠CAD →AD为顶角∠BAC的平分线∠ADB=∠ADC=90° →AD为底边BC上的高 用语言叙述为:性质1 等腰三角形的两个底角相等(简写成“等边对等角”);性质2 等腰三角形的顶角平分线、底边上的中线;底边上的高互相重合.(可简记为“三线合一”性质)设问4:你能用所学的知识验证等腰三角形的性质吗 1.证明等腰三角形底角的性质. 教师要求学生根据猜想的结论画出相应的图形,写出已知和求证.已知:如图1,在△ABC中,AB=AC 求证:∠B=∠C. 师生共同分析证明思路并证明.强调以下两点: (1)利用三角形全等来证明两角相等. 为证∠B=∠C,需证明以∠B,∠C为元素的两个三角形全等,需要添加辅助线构造符合证明要求的两个三角形. (2)添加辅助线的方法可以多样. 例如,常见的作顶角∠BAC的平分线,或作底边BC上的中线或作底边BC上的高等.让学生选择一种辅助线完成证明过程.2.证明等腰三角形的“三线合一”性质.鼓励学生用多种方法证明. 三、学以致用1,已知等腰三角形的一个底角是36°,则其余两角为______ 2,已知等腰三角形一个角是36°,则其余两角为______ 3,已知等腰三角形一个角是110°,则其余两角为______。 四、知识小结1、等腰三角形是轴对称图形; 2、等边对等角的性质;六、作业布置1.必做题:教科书第143页练习1、2、3.2.选做题:教科书第150页习题12.3第8题.
课后反思
课 题 等腰三角形 课型 新授 课时编号
学习目标 通过性质定理和推论运用进一步培养学生分析问题解决问题的能力,渗透转化思想.
学习重难点 重点:等腰三角形性质的应用.难点:添加合适的辅助线.
集 体 备 课 个 性 设 计
一、知识回顾1.等腰三角形的性质定理是什么? 2.等腰三角形一个角为50°,求其它两角.3.等腰三角形一个外角为70°,求三个内角的度数.二、探究新知例1 如图所示已知:△ABC中,AB=AC,点D在AC上,且BD=BC=AD.求:△ABC各角的度数.例2 如图所示,已知:点D、E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE.讨论:(1)等腰三角形底边中点到两腰的距离相等吗?(2)利用类似的方法,还可以得到等腰三角形中哪些线段相等?三、学以致用1.如图所示,已知:AB=AE,BC=ED,∠B=∠E,AM⊥CD.求证:CM=MD.2.如图所示,已知:△ABC和△EBD均为等边三角形,点D在BC上.求证:AD=CE.四、知识小结列方程解几何计算题是几何中常用的方法,要善于将几何的定理、等式转化为代数方程.(2)等腰三角形中常添的辅助线是顶角平分线或底边上的中线和高线.(3)要灵活运用等腰三角形的性质. 五、诊断检测(一)1.等腰△ABC的底角是60°,则顶角是________度.2.等腰三角形“三线合一”是指___________.3.等腰三角形的顶角是n°,则两个底角的角平分线所夹的钝角是_________.4.如图,△ABC中AB=AC,EB=BD=DC=CF,∠A=40°,则∠EDF的度数是_____.5.△ABC中,AB=AC.点D在BC边上 (1)∵AD平分∠BAC,∴_______=________;________⊥_________; (2)∵AD是中线,∴∠________=∠________;________⊥________; (3)∵AD⊥BC,∴∠________=∠_______;_______=_______.六、作业布置如图,AF是△ABC的角平分线,BD⊥AF交AF的延长线于D,DE∥AC交AB于E,求证:AE=BE.
课后反思
课 题 等腰三角形 课型 新授 课时编号
学习目标 ①会阐述、推证等腰三角形的判定定理.②学会比较等腰三角形性质定理和判定定理的联系与区别.
学习重难点 重点:等腰三角形的判定定理的探索和应用.难点:等腰三角形的判定与性质的区别.
集 体 备 课 个 性 设 计
一、知识回顾等腰三角形的性质有哪些?1:等腰三角形的两底角相等.2:等腰三角形的顶角的平分线、底边上的中线、底边上的高互相重合.二、探究新知(一)思考:如图,位于在海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A=∠B.如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)? 在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系? 即:如果一个三角形有两个角相等,那么这个三角形所对的两条边也相等. 如何验证 学生根据命题画出图形,并写出已知、求证.已知:如图,在△ABC中,∠B=∠C.求证:AB=AC学生寻求证明途径.证明:作AD⊥BC,垂足为D,在⊿ABD和⊿ACD中,作∠BAC的平分线AD.在△BAD和△CAD中∴⊿ABD≌ ⊿ACD∴AB=AC[例2]求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形.分析:这个题是文字叙述的证明题,我们首先得将文字语言转化成相应的数学语言,再根据题意画出相应的几何图形.已知:∠CAE是△ABC的外角,∠1=∠2,AD∥BC(如图). 求证:AB=AC.三、学以致用(一)1、如图,∠A=360,∠DBC=360,∠C=720,分别计算∠1、 ∠2的度数。2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?3、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。四、知识小结1.通过这两节课的学习,你学会了几种判断等腰三角形的方法 2.你会比较等腰三角形性质定理与判定定理的联系与区别吗 六、作业布置1.必做题:教科书第145页练习1、2、3.2.选做题:教科书第150页习题12.3第9、10题.
课后反思
课 题 等边三角形 课型 新授 课时编号
学习目标 经历画、折等实践操作活动过程,发展学生的空间观念,,并培养学生的动手实践能力。
学习重难点 重点:等边三角形的性质和判定方法. 难点:等边三角形性质的应用.
集 体 备 课 个 性 设 计
一.欣赏图片,感受生活通过欣赏我发现了 二.小组合作,探究新知(一)1.观察老师给你的等边三角形纸片, 根据等腰三角形的性质,猜想等边三角形有哪些性质?并通过测量、折纸、证明等方式进行验证。探究得出以下性质: (1). (2). (3). (4). 小组合作,探究新知(二)1.等边三角形的三个角都相等,并且每个角都是60°,反之,如果我告诉你一个三角形三个角都相等,你能确定这是等边三角形吗?理由呢?得出结论:(1). 理由: 2.实践应用 如图,课外兴趣小组在一次测量活动中,测得∠APB=60°, AP=BP=200m,他们便得出了一个结论:池塘最长处不小于200m.他们的结论对吗 解:∵AP=BP, ∠APB=60° ∴∠ =∠ = ∴ ∠ = ∠ =∠ 从而△APB是 ,AB的长是 m,由此可以得出兴趣小组的结论是 的。3. .你认为有一个角等于60°的等腰三角形是等边三角形吗? 结论: 三、学以致用1.等边三角形的 相等, 相等。2. △ABC为等边三角形,BD为高,CE为角平分线,BD与CE相交于点O,则,∠ABD= ,∠BOC= .3.等边三角形的对称轴有( ) (A)1条(B)2条(C)3条(D)4条4.下列四个说法中,不正确的有( )(1)三条边都相等的三角形是等边三角形。(2)有两个角等于60°的三角形是等边三角形。(3)有一个是60°的等腰三角形是等边三角形。 (4)等腰三角形是等边三角形。(A)0个(B)1个(C)2个(D)3个5.如图,在等边三角形ABC中,AD是BC上的高,且∠BDE=∠CDF=60°,图中与BD相等的线段有 。四、动手操作,感悟新知在等边三角形ABC的边AB,AC上分别截取 AD=AE△ADE是等边三角形吗?试说明理由。五、拓展思维1.比一比,看谁最聪明如图,是用6根火柴搭建的等边三角形,再给你几根火柴可摆出4个等边三角形?摆一摆,并在右图中画出来。六、走进中考,1.如图,A,B,C三座 城市在一条直线上,A,B,D 三座城市之间距离相等,A,C,E三座城市之间距离也相等.已有公路AB,AD,BD,AC,AE,EC六条,根据经济发展需要,要再建设两条高速公路BE,CD,猜猜BE,CD长度之间有什么关系 七.知识小结等边三角形与等腰三角形在定义,性质和判定的异同
课后反思
课 题 等边三角形 课型 新授 课时编号
学习目标 1.探索──发现──猜想──证明直角三角形中有一个角为30°的性质.2.有一个角为30°的直角三角形的性质的简单应用.
学习重难点 含30°角的直角三角形性质定理的探索与证明.
集 体 备 课 个 性 设 计
一.复习旧知1、等边三角形三边 ,三个角都等于 度.2、等边三角形是轴对称图形,有 条对称轴. 3、 的等腰三角形是等边三角形4。如图,已知△ABC和△BDE都是等边三角形, 求证:AE=CD二.问题情境, 问题:用两个全等的含30°角的直角三角尺,你能拼出一个怎样的三角形?能拼出一个等边三角形吗?说说你的理由. 由此你能想到,在直角三角形中,30°角所对的直角边与斜边有怎样的大小关系?你能证明你的结论吗? 三.动手动脑 我摆出了如下两个三角形 已知:如图,在Rt△ABC中,∠C=90°,∠BAC=30°.求证:BC=AB. 四.小试牛刀1。如图,△ABC中,若AC⊥BC,∠BAC=30°,则∠B=_____°,延长BC到D使BD=AB,连结AD,则△ABD是_____三角形,BC=_____=_____。 2。如图,∠C=90°,D是CA的延长线上一点, ∠BDC=15 °,且AD=AB,则BC= AD3. 如图,在△ABC中, AB=AC=2a且∠ABC=∠ACB=150,CD是腰AB上的高,求CD的长 五.能力提高1。如图,在△ABC中,AB=AC,∠C=30°,DA⊥BA于A,BC=14.4cm,则AD= 2.如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,∠A=30°,立柱BD、DE要多长? 六.总结反思通过这节课的学习,我学到了:
课后反思
课 题 《轴对称》小结 课型 复习 课时编号
学习目标 学生对整章的学习内容做一回顾,系统地把握全章的知识要点和基本技能
学习重难点 教学重点:判断图形是否是轴对称图形教学难点: 灵活运用上述性质解决问题、轴对称图案的设计
集 体 备 课 个 性 设 计
<一> 知识回顾问题1:轴对称图形的定义是什么 它是判断图形是否是轴对称图形的依据。问题2:是否会画轴对称图形的对称轴 找出轴对称图形的任一组对称点,连结对称点,画对称点所连线段的垂直平分线,即得到该图形对称轴。问题3:轴对称图形对称点的连线与对称轴有什么关系 轴对称图形对称点的连线被对称轴垂直平分。问题4:线段垂直平分线、角平分线具有什么性质 线段垂直平分线上的点到线段两端的距离相等;角平分线上的点到角两边的距离相等。问题5:等腰三角形有什么性质 等腰三角形底边的中线、高线、顶角的平分线互相重合,等腰三角形的两个底角相等(等边对等角),等边三角形的三个角都等于60°。问题6:如何判断三角形是等腰三角形 等边三角形 如果一个三角形有两个角相等,那么这两个角所对的边也相等(等角对等边);有两个角是60°的三角形是等边三角形,有一个角是60°的等腰三角形是等边三角形。<三> 例题 基础知识: 1.下列图案是轴对称图形的有( ) A.1个 B.2个 C.3个 D.4个2.如右图所示,下列图形中,一定是轴对称图形的有( )个。线段、三角形、平行四边形、梯形,半圆3.观察下面的英文字母,其中是轴对称图形的有( )个。A,C,D,E,F,H,J,S,M,Y,Z4. 等腰三角形的一个内角是700,则它的另外两个角的度数分别( )。5. 已知1,3,x分别为等腰△ABC的三边长,化简( )6. 等腰三角形的一个外角是40度,则这个等腰三角形的底角等于( )度。7.如图,三角形ABC中,AB=AC,∠A=40度,AB的垂直平分线MN交AC于D,连接BD,∠DBC等于( )度知识拓展:1.如图,△ABC中,∠ABC=1200,AM=AN,CN=CP, 求 ∠MNP的度数.2. 已知AD是等腰三角形一腰上的高,∠DAB=600,求△ABC的三个内角的度数。3如图,△ABC中,AD平分∠CAB交BC于D,且CD=2,∠C=900,∠DEF=900,∠B=∠FDB=22.50,AE=6,DF=4,求AB的长. 4 如图,△ABC中,AB=AC,E 在CA的延长线上,∠AEF=∠AFE,求证:EF⊥BC<四> 课堂小结: 通过本节课复习,同学们应掌握本章知识和技能,并运用所学知识和技能解决问题
课后反思
E
B
A
D
C
F
∠ABC=∠ACB
∠ADB=∠ADC=90度
AD=AD
∵
_
A
_
C
_
B
A
B
C
D
E
O
_
C
_
A
_
B
·
A
B
C
