八年级数学等边三角形(2)
文档属性
| 名称 | 八年级数学等边三角形(2) |  | |
| 格式 | zip | ||
| 文件大小 | 194.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-16 13:38:45 | ||
图片预览



文档简介
(共13张PPT)
知识回顾:
1.等边三角形的三边都相等。
2.等边三角形的内角都相等,且都等于60 °
3.等边三角形是轴对称图形,有三条对称轴
4.等边三角形各边上中线,高和所对角的平分线都三线合一.
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
(2) 等边三角形的判定:
(1).等边三角形的性质
B
A
C
D
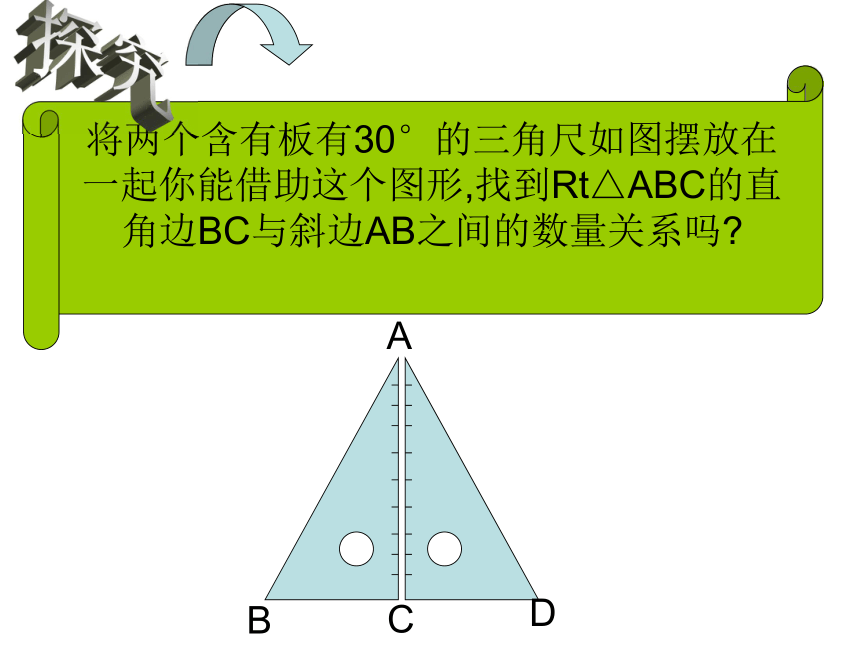
将两个含有板有30°的三角尺如图摆放在
一起你能借助这个图形,找到Rt△ABC的直
角边BC与斜边AB之间的数量关系吗
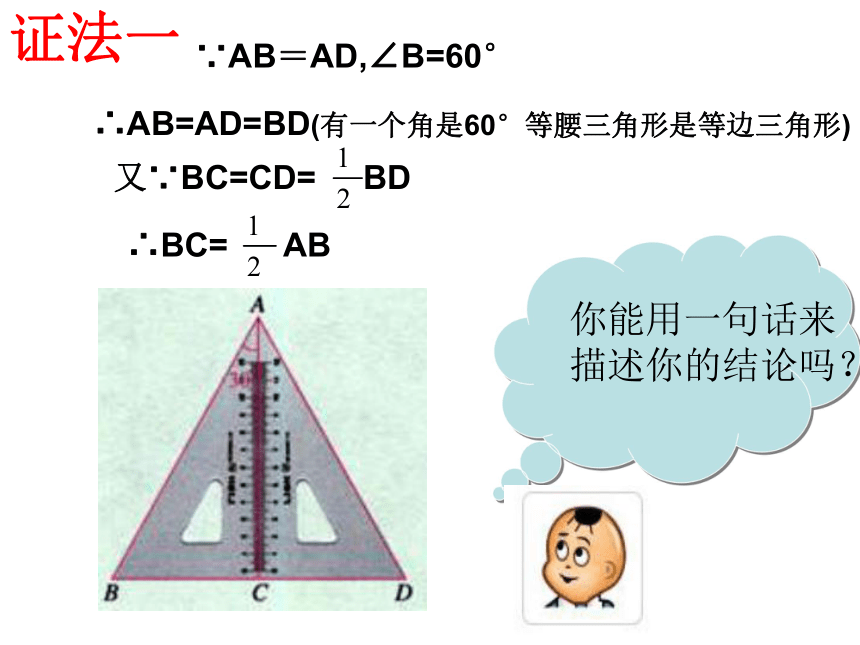
∵AB=AD,∠B=60°
B
A
C
D
你能用一句话来
描述你的结论吗?
∴AB=AD=BD(有一个角是60°等腰三角形是等边三角形)
又∵BC=CD= BD
∴BC= AB
证法一
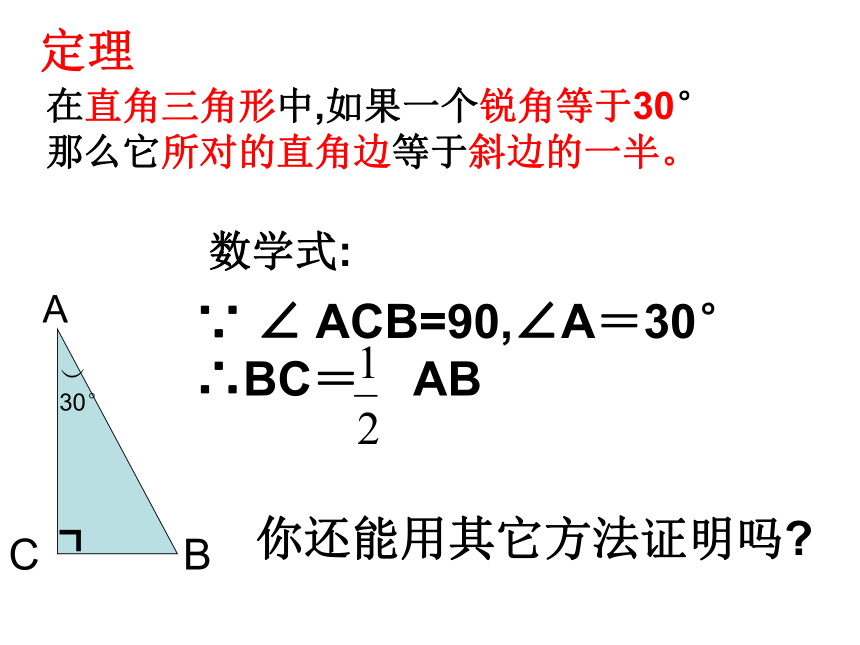
在直角三角形中,如果一个锐角等于30°
那么它所对的直角边等于斜边的一半。
)
A
┓
30°
C
B
数学式:
∵ ∠ ACB=90,∠A=30°
∴BC= AB
你还能用其它方法证明吗
定理
例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、 DE垂直于横梁AC,AB=7.4m,∠A=30°立柱BC 、 DE要多长
A
B
D
E
C
解: ∵DE⊥AC,BC⊥AC, ∠A= 30 °
由上述定理可得:
BC=1/2AB,DE=1/2AD,
∴BC=1/2×7.4=3.7(m)
又AD=1/2AB,=
∴DE=1/2AD=1/2×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.
′
解:过C作BA延长线的垂线CD,垂足为D
∵∠B=∠ACB=150(已知),
∴∠DAC=∠B+∠ACB= 150+150=300
(三角形的一个外角,等于和不相邻的两内角的和).
∴CD= AC= ×2a=a
(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半).
A
C
B
D
150
150
例2.已知:等腰三角形的底角为150,腰长为2a.
求:腰上的高.
2a
2、在Rt△ABC 中, 如果∠BCA= 90° , ∠A= 30 °,CD是高,
(1)BD=1,则BC、AB各等于多少;
(2)求证:BD=1/2BC=1/4AB
解(1)由已知可求得
∠BCD= 30 °
于是在Rt△ADC 与Rt△BDC
中用本定理得BC=2,AB=4
(2)在Rt△ADC 与Rt△BDC运用本定理
BD=1/2BC
BC=1/2AB
∴ BD=1/2BC=1/4AB
A
C
B
D
要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
A
C
B
┓
变题:如果将这块地均匀分给
甲乙丙丁四家农户呢?
:
1在Rt△ABC 中, ∠C= 90°,
∠B= 2 ∠A,问∠B 、∠A各是多少度?
边AB与BC之间有什么关系?
1 如图,在△ABC 中∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于M,且BD=8㎝,求AC之长.
M
C
B
D
A
2 如图,在△ABC 中,AB=AC, ∠A=120°,AB的垂直平分线
MN交BC于M,交AB于N,
求证:CM=2BM
N
M
C
B
A
知识回顾:
1.等边三角形的三边都相等。
2.等边三角形的内角都相等,且都等于60 °
3.等边三角形是轴对称图形,有三条对称轴
4.等边三角形各边上中线,高和所对角的平分线都三线合一.
1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.
(2) 等边三角形的判定:
(1).等边三角形的性质
B
A
C
D
将两个含有板有30°的三角尺如图摆放在
一起你能借助这个图形,找到Rt△ABC的直
角边BC与斜边AB之间的数量关系吗
∵AB=AD,∠B=60°
B
A
C
D
你能用一句话来
描述你的结论吗?
∴AB=AD=BD(有一个角是60°等腰三角形是等边三角形)
又∵BC=CD= BD
∴BC= AB
证法一
在直角三角形中,如果一个锐角等于30°
那么它所对的直角边等于斜边的一半。
)
A
┓
30°
C
B
数学式:
∵ ∠ ACB=90,∠A=30°
∴BC= AB
你还能用其它方法证明吗
定理
例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、 DE垂直于横梁AC,AB=7.4m,∠A=30°立柱BC 、 DE要多长
A
B
D
E
C
解: ∵DE⊥AC,BC⊥AC, ∠A= 30 °
由上述定理可得:
BC=1/2AB,DE=1/2AD,
∴BC=1/2×7.4=3.7(m)
又AD=1/2AB,=
∴DE=1/2AD=1/2×3.7=1.85(m).
答:立柱BC、DE分别要3.7m、1.85m.
′
解:过C作BA延长线的垂线CD,垂足为D
∵∠B=∠ACB=150(已知),
∴∠DAC=∠B+∠ACB= 150+150=300
(三角形的一个外角,等于和不相邻的两内角的和).
∴CD= AC= ×2a=a
(在直角三角形中, 如果有一个锐角等于300,那么它所对的直角边等于斜边的一半).
A
C
B
D
150
150
例2.已知:等腰三角形的底角为150,腰长为2a.
求:腰上的高.
2a
2、在Rt△ABC 中, 如果∠BCA= 90° , ∠A= 30 °,CD是高,
(1)BD=1,则BC、AB各等于多少;
(2)求证:BD=1/2BC=1/4AB
解(1)由已知可求得
∠BCD= 30 °
于是在Rt△ADC 与Rt△BDC
中用本定理得BC=2,AB=4
(2)在Rt△ADC 与Rt△BDC运用本定理
BD=1/2BC
BC=1/2AB
∴ BD=1/2BC=1/4AB
A
C
B
D
要把一块三角形的土地均匀分给甲 、 乙、丙三家农户去种植,如果∠C=90°∠B=30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出来.
A
C
B
┓
变题:如果将这块地均匀分给
甲乙丙丁四家农户呢?
:
1在Rt△ABC 中, ∠C= 90°,
∠B= 2 ∠A,问∠B 、∠A各是多少度?
边AB与BC之间有什么关系?
1 如图,在△ABC 中∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于M,且BD=8㎝,求AC之长.
M
C
B
D
A
2 如图,在△ABC 中,AB=AC, ∠A=120°,AB的垂直平分线
MN交BC于M,交AB于N,
求证:CM=2BM
N
M
C
B
A
