2021—2022学年人教版数学七年级上册_4.3.3余角和补角 课件(共16张ppt)
文档属性
| 名称 | 2021—2022学年人教版数学七年级上册_4.3.3余角和补角 课件(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 703.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 21:31:58 | ||
图片预览





文档简介
(共16张PPT)
课 前 寄 语
如果要挖井,
就要挖到水出为止。
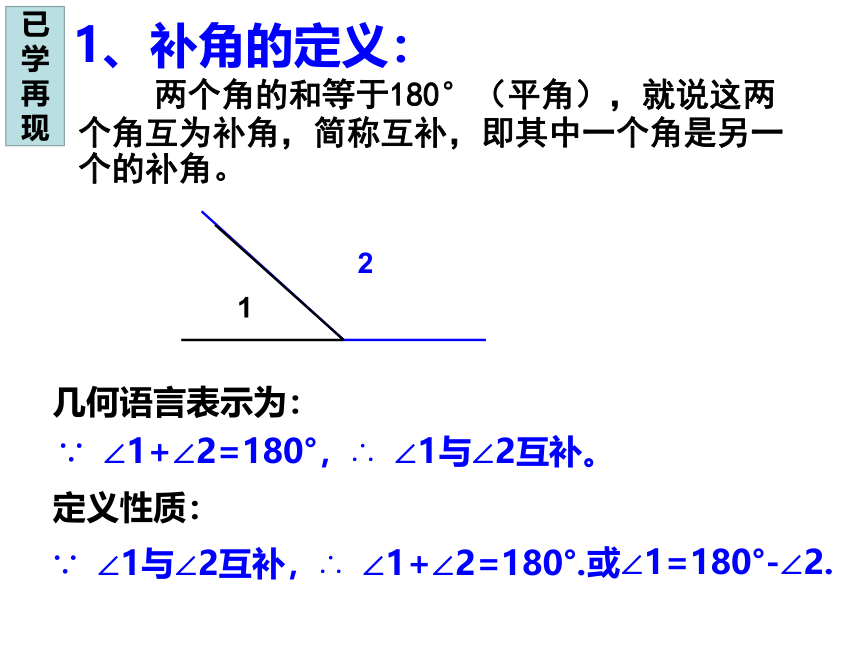
两个角的和等于180°(平角),就说这两个角互为补角,简称互补,即其中一个角是另一个的补角。
1
2
1、补角的定义:
几何语言表示为:
定义性质:
∵ ∠1+∠2=180°,∴ ∠1与∠2互补。
∵ ∠1与∠2互补,∴ ∠1+∠2=180°.
已学再现
或∠1=180°-∠2.
两个角的和等于90°(直角),就说这两个角互为余角,简称互余,即其中一个角是另一个角的余角。
几何语言表示为:
O
A
D
1
2
定义性质:
2、余角的定义:
∵ ∠1+∠2=90°,∴ ∠1与∠2互余。
∵ ∠1与∠2互余,∴ ∠1+∠2=90°.
已学再现
或∠1=90°-∠2.
角的互补(互余)关系与角的位置无关!
只需满足数量关系和为180°(90°)!
角的互补(或互余)关系,是角的什么关系?
数量关系
已学再现
1、求任意一个角的余角,就用900减去这个角就可以得到,同理,求任意一个角的补角,就用1800减去这个角就可以得到。
2、同一个角的补角比它的余角大900.
1、如何求一个角的余角和补角?
2、同一个角的余角和补角的关系?
已学再现
4.3.3 余角与补角
——性质
学习目标
余角性质:同角(等角)的余角相等
补角性质:同角(等角)的补角相等
用代数(方程)思想解决几何问题
两个
知识点
一个思想:
如果
∠1与∠2互余,
∠3与∠4互余,
∠1=∠3,
那么∠2与∠4 什么关系
结论:
(答:∠2=∠4 )
2
3
1
4
等角的余角相等
想一想
如图,∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
∵∠1与∠2互余,∠3与∠4互余(已知)
∴ ∠2=90°─∠1,∠4=90°─∠3(互为余角的定义)
∵ ∠1=∠3(已知)
∴ ∠2=∠4(等量减等量差相等)
等角的余角相等
证
明
同角
余角性质
结论:∠2 =∠4
同角(等角)的余角相等
证明:
如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3那么∠2与∠4相等吗?为什么?
1
4
3
2
结 论:等角的补角相等
(答:∠2=∠4)
仿照以上余角结论的证明,大家尝试着完成这个结论的证明
同角
补角性质:同角(等角)的补角相等
想一想
牛刀小试
1、若∠1+∠2= 90 °,∠1+∠3=90°,
则_____________。
2、若∠1+∠2=90°,∠3+∠4=90°
且∠1=∠3,则___________。
3、若∠A=∠B,且∠A+∠1=180°,
∠B+∠2=180°,则____________。
4、∵∠1+∠2=180°,∠1 +∠3= 180°
∴____________。
∠2= ∠3
∠2= ∠4
∠1= ∠2
∠2= ∠3
勇攀高峰
.
∠1,∠2都是∠3的补角,根据________________
得∠1=∠2。
同角的补角相等
设这个角为 ,则它的余角是 ,它的补角是
已知一个角的补角是这个角的余角的3倍,求这个角的度数。
答:这个角为
解:
拓展:
由题意得:
一个角
补角
余角
解得:
用代数(方程)思想解决几何问题
自我检测
.
已知一个角的补角和这个角的余角互补,求这个角的度数。
同角(等角)的余角相等
同角(等角)的补角相等
用代数(方程)思想解决几何问题
一个思想
余角性质
补角性质
课时小结
作 业
《学习之友》P80 课后作业T1、2
课 前 寄 语
如果要挖井,
就要挖到水出为止。
两个角的和等于180°(平角),就说这两个角互为补角,简称互补,即其中一个角是另一个的补角。
1
2
1、补角的定义:
几何语言表示为:
定义性质:
∵ ∠1+∠2=180°,∴ ∠1与∠2互补。
∵ ∠1与∠2互补,∴ ∠1+∠2=180°.
已学再现
或∠1=180°-∠2.
两个角的和等于90°(直角),就说这两个角互为余角,简称互余,即其中一个角是另一个角的余角。
几何语言表示为:
O
A
D
1
2
定义性质:
2、余角的定义:
∵ ∠1+∠2=90°,∴ ∠1与∠2互余。
∵ ∠1与∠2互余,∴ ∠1+∠2=90°.
已学再现
或∠1=90°-∠2.
角的互补(互余)关系与角的位置无关!
只需满足数量关系和为180°(90°)!
角的互补(或互余)关系,是角的什么关系?
数量关系
已学再现
1、求任意一个角的余角,就用900减去这个角就可以得到,同理,求任意一个角的补角,就用1800减去这个角就可以得到。
2、同一个角的补角比它的余角大900.
1、如何求一个角的余角和补角?
2、同一个角的余角和补角的关系?
已学再现
4.3.3 余角与补角
——性质
学习目标
余角性质:同角(等角)的余角相等
补角性质:同角(等角)的补角相等
用代数(方程)思想解决几何问题
两个
知识点
一个思想:
如果
∠1与∠2互余,
∠3与∠4互余,
∠1=∠3,
那么∠2与∠4 什么关系
结论:
(答:∠2=∠4 )
2
3
1
4
等角的余角相等
想一想
如图,∠1与∠2互余,∠3与∠4互余,如果∠1=∠3,那么∠2与∠4相等吗?为什么?
1
2
3
4
∵∠1与∠2互余,∠3与∠4互余(已知)
∴ ∠2=90°─∠1,∠4=90°─∠3(互为余角的定义)
∵ ∠1=∠3(已知)
∴ ∠2=∠4(等量减等量差相等)
等角的余角相等
证
明
同角
余角性质
结论:∠2 =∠4
同角(等角)的余角相等
证明:
如图,∠1与∠2互补,∠3与∠4互补,如果∠1=∠3那么∠2与∠4相等吗?为什么?
1
4
3
2
结 论:等角的补角相等
(答:∠2=∠4)
仿照以上余角结论的证明,大家尝试着完成这个结论的证明
同角
补角性质:同角(等角)的补角相等
想一想
牛刀小试
1、若∠1+∠2= 90 °,∠1+∠3=90°,
则_____________。
2、若∠1+∠2=90°,∠3+∠4=90°
且∠1=∠3,则___________。
3、若∠A=∠B,且∠A+∠1=180°,
∠B+∠2=180°,则____________。
4、∵∠1+∠2=180°,∠1 +∠3= 180°
∴____________。
∠2= ∠3
∠2= ∠4
∠1= ∠2
∠2= ∠3
勇攀高峰
.
∠1,∠2都是∠3的补角,根据________________
得∠1=∠2。
同角的补角相等
设这个角为 ,则它的余角是 ,它的补角是
已知一个角的补角是这个角的余角的3倍,求这个角的度数。
答:这个角为
解:
拓展:
由题意得:
一个角
补角
余角
解得:
用代数(方程)思想解决几何问题
自我检测
.
已知一个角的补角和这个角的余角互补,求这个角的度数。
同角(等角)的余角相等
同角(等角)的补角相等
用代数(方程)思想解决几何问题
一个思想
余角性质
补角性质
课时小结
作 业
《学习之友》P80 课后作业T1、2
