北师大版 二年级上册数学 式的规律 课件(共15张PPT)
文档属性
| 名称 | 北师大版 二年级上册数学 式的规律 课件(共15张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 12:24:17 | ||
图片预览



文档简介
(共15张PPT)
式的规律
知识讲解
× 1 2 3 4 5 6 7 8 9
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6 7×1=7 8×1=8 9×1=9
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12 7×2=14 8×2=16 9×2=18
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18 7×3=21 8×3=24 9×3=27
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24 7×4=28 8×4=32 9×4=36
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30 7×5=35 8×5=40 9×5=45
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36 7×6=42 8×6=48 9×6=54
7 1×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=49 8×7=56 9×7=63
8 1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=64 9×8=72
9 1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81
情境引入
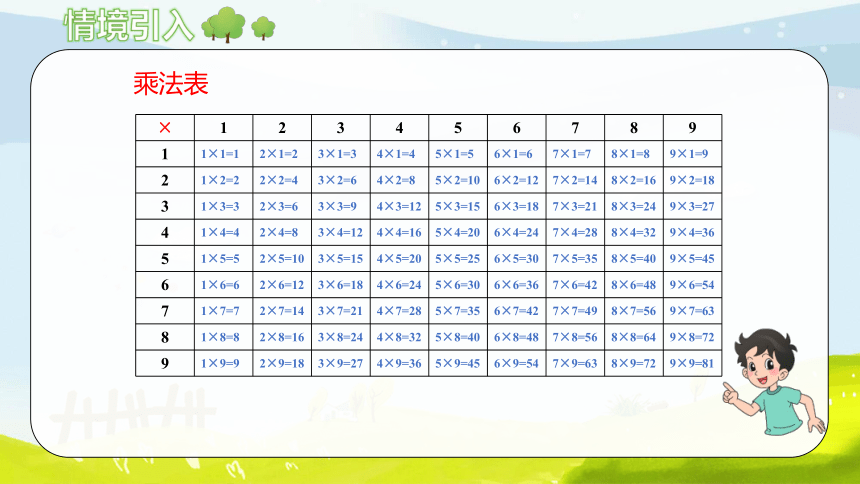
乘法表
1
【 知识精讲】
3
【典型例题】
2
【 易错易误点 】
知识精讲
× 1 2 3 4 5 6 7 8 9
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6 7×1=7 8×1=8 9×1=9
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12 7×2=14 8×2=16 9×2=18
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18 7×3=21 8×3=24 9×3=27
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24 7×4=28 8×4=32 9×4=36
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30 7×5=35 8×5=40 9×5=45
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36 7×6=42 8×6=48 9×6=54
7 1×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=49 8×7=56 9×7=63
8 1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=64 9×8=72
9 1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81
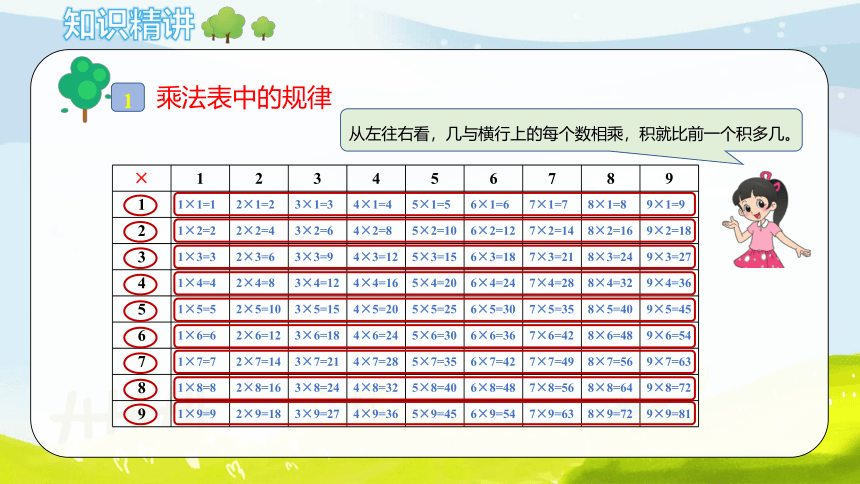
从左往右看,几与横行上的每个数相乘,积就比前一个积多几。
知识精讲
乘法表中的规律
1
× 1 2 3 4 5 6 7 8 9
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6 7×1=7 8×1=8 9×1=9
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12 7×2=14 8×2=16 9×2=18
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18 7×3=21 8×3=24 9×3=27
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24 7×4=28 8×4=32 9×4=36
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30 7×5=35 8×5=40 9×5=45
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36 7×6=42 8×6=48 9×6=54
7 1×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=49 8×7=56 9×7=63
8 1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=64 9×8=72
9 1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81
知识精讲
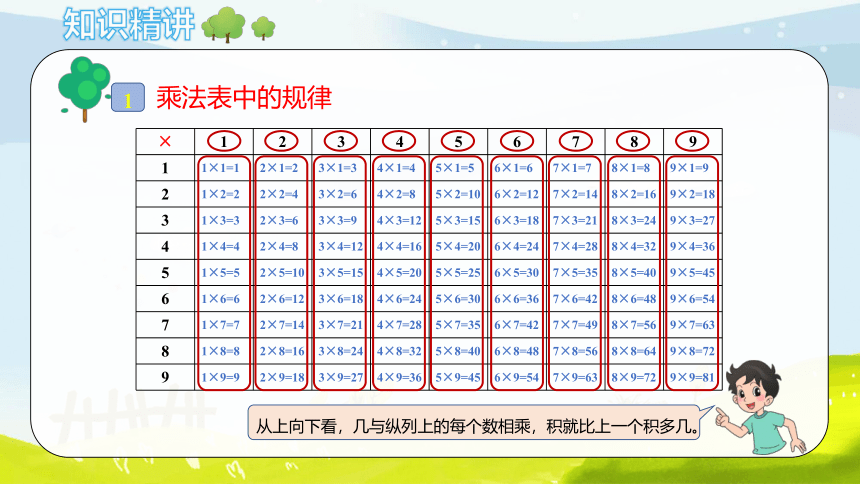
从上向下看,几与纵列上的每个数相乘,积就比上一个积多几。
乘法表中的规律
1
知识精讲
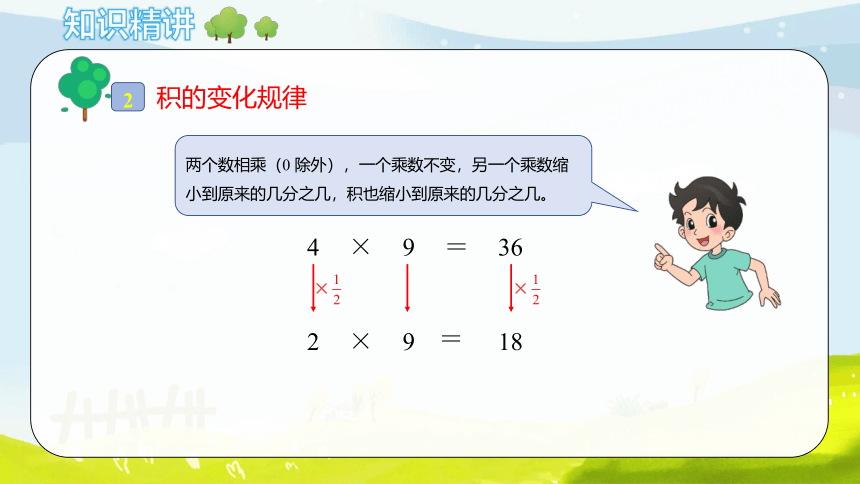
积的变化规律
2
2
×
3
4
=
6
×
3
=
12
两个数相乘(0 除外),一个乘数不变,另一个乘数扩大到原来的几倍,积也扩大相同的倍数。
×2
×2
知识精讲
积的变化规律
2
4
×
9
2
=
36
×
9
=
18
两个数相乘(0 除外),一个乘数不变,另一个乘数缩小到原来的几分之几,积也缩小到原来的几分之几。
×
×
知识精讲
2
两个数相乘( 0 除外),一个乘数扩大到原来的 a 倍,另一个乘数扩大到原来的 b 倍,积扩大到原来的(a×b)倍。
积的变化规律
2
×
3
4
=
6
×
9
=
36
×2
×3
×(2×3)
细心观察算式中的每一部分。
既要观察算式的特点,也要观察得数的特点。
12×9+3=111
123×9+4=1111
1234×9+5=11111
1234567×9+8=
12345678×9+9=
……
知识精讲
3
算式中的规律
11111111
111111111
1×9+2=11
1
【 知识精讲】
3
【典型例题】
2
【 易错易误点 】
易错
易误点
易错易误点
易错
对式子观察不够全面
25 × 4 = 100
本题中,乘数 25 和 4 都扩大到原来的 10 倍,积应该扩大到原来的 10×10=100 倍。所以,250×40=10000。
250 × 40 =
×10
×10
1000
10000
×100
1
【 知识精讲】
3
【典型例题】
2
【 易错易误点 】
典型例题
典型例题
请根据12345679×9=111111111,写出下面各算式的答案。
12345679×18=
12345679×27=
12345679×81=
12345679×( )=444444444
12345679×( )=666666666
12345679×9×2
=111111111×2
=222222222
先观察算式,前面 3 道题都是两个数相乘,其中一个乘数都是 12345679,另一个乘数扩大到题干中乘数“9”的几倍,因此根据积的变化规律,积也要扩大到原来相应的几倍。
333333333
999999999
典型例题
请根据12345679×9=111111111,写出下面各算式的答案。
12345679×18=
12345679×27=
12345679×81=
12345679×( )=444444444
12345679×( )=666666666
222222222
333333333
999999999
后面 2 道题是前面几题的逆向变换,其中一个乘数 12345679 没有发生变化,但积扩大到题干中积一定的倍数,因此另一个乘数也应扩大到“9”相应的倍数。
36
54
同学们,再见!
式的规律
知识讲解
× 1 2 3 4 5 6 7 8 9
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6 7×1=7 8×1=8 9×1=9
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12 7×2=14 8×2=16 9×2=18
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18 7×3=21 8×3=24 9×3=27
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24 7×4=28 8×4=32 9×4=36
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30 7×5=35 8×5=40 9×5=45
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36 7×6=42 8×6=48 9×6=54
7 1×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=49 8×7=56 9×7=63
8 1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=64 9×8=72
9 1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81
情境引入
乘法表
1
【 知识精讲】
3
【典型例题】
2
【 易错易误点 】
知识精讲
× 1 2 3 4 5 6 7 8 9
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6 7×1=7 8×1=8 9×1=9
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12 7×2=14 8×2=16 9×2=18
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18 7×3=21 8×3=24 9×3=27
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24 7×4=28 8×4=32 9×4=36
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30 7×5=35 8×5=40 9×5=45
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36 7×6=42 8×6=48 9×6=54
7 1×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=49 8×7=56 9×7=63
8 1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=64 9×8=72
9 1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81
从左往右看,几与横行上的每个数相乘,积就比前一个积多几。
知识精讲
乘法表中的规律
1
× 1 2 3 4 5 6 7 8 9
1 1×1=1 2×1=2 3×1=3 4×1=4 5×1=5 6×1=6 7×1=7 8×1=8 9×1=9
2 1×2=2 2×2=4 3×2=6 4×2=8 5×2=10 6×2=12 7×2=14 8×2=16 9×2=18
3 1×3=3 2×3=6 3×3=9 4×3=12 5×3=15 6×3=18 7×3=21 8×3=24 9×3=27
4 1×4=4 2×4=8 3×4=12 4×4=16 5×4=20 6×4=24 7×4=28 8×4=32 9×4=36
5 1×5=5 2×5=10 3×5=15 4×5=20 5×5=25 6×5=30 7×5=35 8×5=40 9×5=45
6 1×6=6 2×6=12 3×6=18 4×6=24 5×6=30 6×6=36 7×6=42 8×6=48 9×6=54
7 1×7=7 2×7=14 3×7=21 4×7=28 5×7=35 6×7=42 7×7=49 8×7=56 9×7=63
8 1×8=8 2×8=16 3×8=24 4×8=32 5×8=40 6×8=48 7×8=56 8×8=64 9×8=72
9 1×9=9 2×9=18 3×9=27 4×9=36 5×9=45 6×9=54 7×9=63 8×9=72 9×9=81
知识精讲
从上向下看,几与纵列上的每个数相乘,积就比上一个积多几。
乘法表中的规律
1
知识精讲
积的变化规律
2
2
×
3
4
=
6
×
3
=
12
两个数相乘(0 除外),一个乘数不变,另一个乘数扩大到原来的几倍,积也扩大相同的倍数。
×2
×2
知识精讲
积的变化规律
2
4
×
9
2
=
36
×
9
=
18
两个数相乘(0 除外),一个乘数不变,另一个乘数缩小到原来的几分之几,积也缩小到原来的几分之几。
×
×
知识精讲
2
两个数相乘( 0 除外),一个乘数扩大到原来的 a 倍,另一个乘数扩大到原来的 b 倍,积扩大到原来的(a×b)倍。
积的变化规律
2
×
3
4
=
6
×
9
=
36
×2
×3
×(2×3)
细心观察算式中的每一部分。
既要观察算式的特点,也要观察得数的特点。
12×9+3=111
123×9+4=1111
1234×9+5=11111
1234567×9+8=
12345678×9+9=
……
知识精讲
3
算式中的规律
11111111
111111111
1×9+2=11
1
【 知识精讲】
3
【典型例题】
2
【 易错易误点 】
易错
易误点
易错易误点
易错
对式子观察不够全面
25 × 4 = 100
本题中,乘数 25 和 4 都扩大到原来的 10 倍,积应该扩大到原来的 10×10=100 倍。所以,250×40=10000。
250 × 40 =
×10
×10
1000
10000
×100
1
【 知识精讲】
3
【典型例题】
2
【 易错易误点 】
典型例题
典型例题
请根据12345679×9=111111111,写出下面各算式的答案。
12345679×18=
12345679×27=
12345679×81=
12345679×( )=444444444
12345679×( )=666666666
12345679×9×2
=111111111×2
=222222222
先观察算式,前面 3 道题都是两个数相乘,其中一个乘数都是 12345679,另一个乘数扩大到题干中乘数“9”的几倍,因此根据积的变化规律,积也要扩大到原来相应的几倍。
333333333
999999999
典型例题
请根据12345679×9=111111111,写出下面各算式的答案。
12345679×18=
12345679×27=
12345679×81=
12345679×( )=444444444
12345679×( )=666666666
222222222
333333333
999999999
后面 2 道题是前面几题的逆向变换,其中一个乘数 12345679 没有发生变化,但积扩大到题干中积一定的倍数,因此另一个乘数也应扩大到“9”相应的倍数。
36
54
同学们,再见!
