2021-2022学年高一上学期数学人教A版(2019)必修第一册5.1.1任意角(课件)(共19张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.1.1任意角(课件)(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 22:36:42 | ||
图片预览





文档简介
(共19张PPT)
5.1.1任意角
初中:(静止)
从一点出发的两条射线所围成的图形
(一)那些年,我们一起学过的角?
知识回顾
锐角 直角 钝角
平角 周角
(二)说一说这些角的范围?
(三)在现实生活中有没有不在 范围内的角?
(三)在现实生活中有没有不在 范围内的角?
实例1:2020东京奥运会双人10米跳水中国选手张家齐,陈芋汐夺得冠军!
(此视频为最后一轮部分)
她们转体多少度?
实例2:将时钟调快4小时,分针如何调?调慢4小时呢?
(时针1小时,分针转一圈)
(三)在现实生活中有没有不在 范围内的角?
实例3:齿轮旋转形成的角
发现:角是由“旋转”而来!
实例1:向后翻腾两周半、转体一周半屈体这样的动作,这里的旋转量都比360°(一周)大,表明角具有任意性.
实例2:顺时针、逆时针表明角具有方向性.
因此,需要对角的概念进行推广.
始边
终边
顶点
B
o
A
新定义
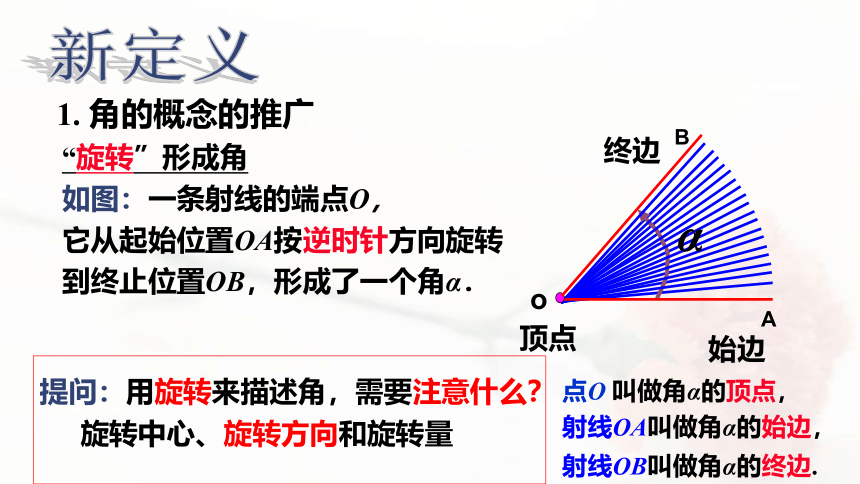
1. 角的概念的推广
点O 叫做角α的顶点,
射线OA叫做角α的始边,
射线OB叫做角α的终边.
“旋转”形成角
如图:一条射线的端点O,
它从起始位置OA按逆时针方向旋转到终止位置OB,形成了一个角α.
α
提问:用旋转来描述角,需要注意什么?
旋转中心、旋转方向和旋转量
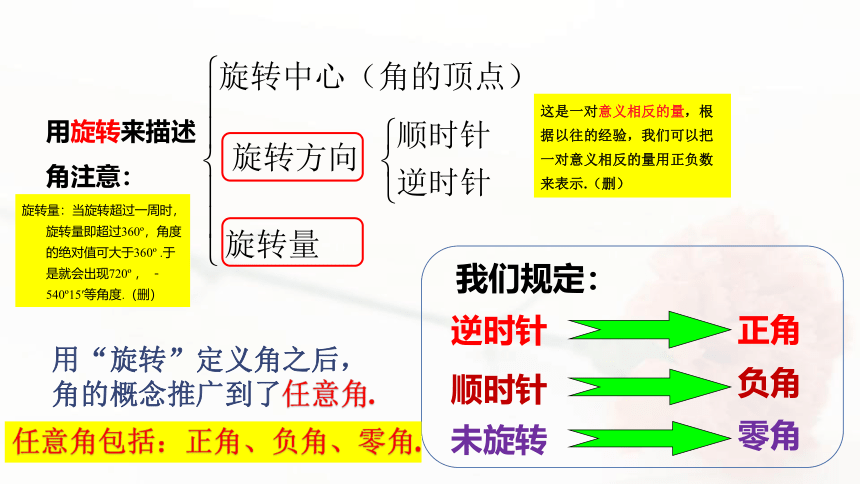
用旋转来描述角注意:
这是一对意义相反的量,根据以往的经验,我们可以把一对意义相反的量用正负数来表示.(删)
逆时针
正角
顺时针
负角
未旋转
零角
我们规定:
旋转量:当旋转超过一周时,旋转量即超过360 ,角度的绝对值可大于360 .于是就会出现720 , - 540 15′等角度.(删)
用“旋转”定义角之后,角的概念推广到了任意角.
任意角包括:正角、负角、零角.
1.手表快了1.5小时,为了将它校准,如何调?
(时针1小时,分针转一圈)
将分针逆时针旋转
360 +180 = 540°
2.手表慢了1.5小时,如何调?
生活小能手
将分针顺时针旋转
-360 -180 = -540°
那一年,我们一起画出来的60°角.
B
A
O
B
A
O
B
A
O
小李同学
小华同学
小明同学
都对,但是乱!
2.象限角
角的顶点与坐标原点重合,
角的始边与x轴的非负半轴重合.
如果角的终边落在坐标轴上,
则该角不属于任何一个象限.
y
x
O
角的终边
角的始边
终边落在第几象限就是第几象限角
Y
Y
y
x
O
2.象限角
角的顶点与坐标原点重合,
角的始边与x轴的非负半轴重合.
终边落在第几象限就是第几象限角
终边
终边
终边
终边
在直角坐标系中画出下列角,并指出下面的角是第几象限角?
(1)-50°
(2)405°
(3)210°
(4)-200°
(5)-450°
看谁答得快
探究:在直角坐标系中,
给定一个角,这个角的终边唯一确定,
若给一条射线作终边,这个角唯一吗
y
x
B
O
角的终边
角的始边
动手:在直角坐标系中画出-30°,330°,-390°,
这些角有什么内在联系?
330°=-30°+360°
-390°=-30°+(-1)×360°
-32°
-390°
x
y
o
330°
{β︱β= -30°+ k·360°,k∈Z}
归纳: 与 -30°角终边相同的角
相差360°的整数倍
{β︱β= -30°+ k·360°,k∈Z}
归纳: 与 -30°角终边相同的角
举一反三:写出与45°,-60°, 终边相同的角的集合.
{β︱β=-60 °+ k·360°,k∈Z}
{β︱β= 45° + k·360°,k∈Z}
任意角α
终边相同的角的集合:
你知道吗?
(1)终边相同的角一定相等吗
(2)锐角是第几象限?
第一象限角一定是锐角吗?
例1. 在0 —360 范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角.
(1) 640 ; (2)-120 .
解:⑴∵640 =360 +280 ,
∴280 的角与640 的角终边相同,
它是第四象限角.
⑵ ∵-120 =-360 +240 ,
∴240 的角与-120 的角终边相同,
它是第三象限角.
追问:再写出与上述各角终边相同的角的集合.
例2. 写出终边在y轴的角的集合.
解:在0°~360°范围内,终边在y轴上的角有两个,即90°,270°角.
因此,所有与90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.
Y
X
O
于是,终边在y轴上的角的集合S=S1∪S2
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+180°+2k·180°,k∈Z}
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }.
追问:
写出终边在x轴的角的集合.
课堂小结
2. 任意角包括哪几类角?
1. 角是如何推广的?
3. 象限角是如何定义的
4. 终边相同的角的集合如何表示
D
1.下列说法中正确的是( )
A.第一象限角是锐角
B.小于90 的角是第一象限角
C.小于90 的角是锐角
D.锐角一定是第一象限角
你学会了吗?
3.写出终边在y=x的角的集合.
{β|β=45°+k·180°,k∈Z }
2.已知角
(1)在0°~360°范围内,找出与α终边相同的角,并指出是第几象限角.
(2)写出与α终边相同的角的集合.
135 ,第二象限角
{β|β=-225°+k·360°,k∈Z }
α= -225 ,
最后希望同学们珍惜时间,
不负韶华!
5.1.1任意角
初中:(静止)
从一点出发的两条射线所围成的图形
(一)那些年,我们一起学过的角?
知识回顾
锐角 直角 钝角
平角 周角
(二)说一说这些角的范围?
(三)在现实生活中有没有不在 范围内的角?
(三)在现实生活中有没有不在 范围内的角?
实例1:2020东京奥运会双人10米跳水中国选手张家齐,陈芋汐夺得冠军!
(此视频为最后一轮部分)
她们转体多少度?
实例2:将时钟调快4小时,分针如何调?调慢4小时呢?
(时针1小时,分针转一圈)
(三)在现实生活中有没有不在 范围内的角?
实例3:齿轮旋转形成的角
发现:角是由“旋转”而来!
实例1:向后翻腾两周半、转体一周半屈体这样的动作,这里的旋转量都比360°(一周)大,表明角具有任意性.
实例2:顺时针、逆时针表明角具有方向性.
因此,需要对角的概念进行推广.
始边
终边
顶点
B
o
A
新定义
1. 角的概念的推广
点O 叫做角α的顶点,
射线OA叫做角α的始边,
射线OB叫做角α的终边.
“旋转”形成角
如图:一条射线的端点O,
它从起始位置OA按逆时针方向旋转到终止位置OB,形成了一个角α.
α
提问:用旋转来描述角,需要注意什么?
旋转中心、旋转方向和旋转量
用旋转来描述角注意:
这是一对意义相反的量,根据以往的经验,我们可以把一对意义相反的量用正负数来表示.(删)
逆时针
正角
顺时针
负角
未旋转
零角
我们规定:
旋转量:当旋转超过一周时,旋转量即超过360 ,角度的绝对值可大于360 .于是就会出现720 , - 540 15′等角度.(删)
用“旋转”定义角之后,角的概念推广到了任意角.
任意角包括:正角、负角、零角.
1.手表快了1.5小时,为了将它校准,如何调?
(时针1小时,分针转一圈)
将分针逆时针旋转
360 +180 = 540°
2.手表慢了1.5小时,如何调?
生活小能手
将分针顺时针旋转
-360 -180 = -540°
那一年,我们一起画出来的60°角.
B
A
O
B
A
O
B
A
O
小李同学
小华同学
小明同学
都对,但是乱!
2.象限角
角的顶点与坐标原点重合,
角的始边与x轴的非负半轴重合.
如果角的终边落在坐标轴上,
则该角不属于任何一个象限.
y
x
O
角的终边
角的始边
终边落在第几象限就是第几象限角
Y
Y
y
x
O
2.象限角
角的顶点与坐标原点重合,
角的始边与x轴的非负半轴重合.
终边落在第几象限就是第几象限角
终边
终边
终边
终边
在直角坐标系中画出下列角,并指出下面的角是第几象限角?
(1)-50°
(2)405°
(3)210°
(4)-200°
(5)-450°
看谁答得快
探究:在直角坐标系中,
给定一个角,这个角的终边唯一确定,
若给一条射线作终边,这个角唯一吗
y
x
B
O
角的终边
角的始边
动手:在直角坐标系中画出-30°,330°,-390°,
这些角有什么内在联系?
330°=-30°+360°
-390°=-30°+(-1)×360°
-32°
-390°
x
y
o
330°
{β︱β= -30°+ k·360°,k∈Z}
归纳: 与 -30°角终边相同的角
相差360°的整数倍
{β︱β= -30°+ k·360°,k∈Z}
归纳: 与 -30°角终边相同的角
举一反三:写出与45°,-60°, 终边相同的角的集合.
{β︱β=-60 °+ k·360°,k∈Z}
{β︱β= 45° + k·360°,k∈Z}
任意角α
终边相同的角的集合:
你知道吗?
(1)终边相同的角一定相等吗
(2)锐角是第几象限?
第一象限角一定是锐角吗?
例1. 在0 —360 范围内,找出与下列各角终边相同的角,并判断它是哪个象限的角.
(1) 640 ; (2)-120 .
解:⑴∵640 =360 +280 ,
∴280 的角与640 的角终边相同,
它是第四象限角.
⑵ ∵-120 =-360 +240 ,
∴240 的角与-120 的角终边相同,
它是第三象限角.
追问:再写出与上述各角终边相同的角的集合.
例2. 写出终边在y轴的角的集合.
解:在0°~360°范围内,终边在y轴上的角有两个,即90°,270°角.
因此,所有与90°角终边相同的角构成集合
S1={β|β=90°+k·360°.k∈Z}.
所有与270°角终边相同的角构成集合
S2={β|β=270°+k·360°.k∈Z}.
Y
X
O
于是,终边在y轴上的角的集合S=S1∪S2
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+180°+2k·180°,k∈Z}
={β|β=90°+2k·180°,k∈Z }
∪{β|β=90°+(2k+1)180°,k∈Z }
={β|β=90°+n·180°,n∈Z }.
追问:
写出终边在x轴的角的集合.
课堂小结
2. 任意角包括哪几类角?
1. 角是如何推广的?
3. 象限角是如何定义的
4. 终边相同的角的集合如何表示
D
1.下列说法中正确的是( )
A.第一象限角是锐角
B.小于90 的角是第一象限角
C.小于90 的角是锐角
D.锐角一定是第一象限角
你学会了吗?
3.写出终边在y=x的角的集合.
{β|β=45°+k·180°,k∈Z }
2.已知角
(1)在0°~360°范围内,找出与α终边相同的角,并指出是第几象限角.
(2)写出与α终边相同的角的集合.
135 ,第二象限角
{β|β=-225°+k·360°,k∈Z }
α= -225 ,
最后希望同学们珍惜时间,
不负韶华!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
