第二章点、直线、平面之间的位置关系复习
文档属性
| 名称 | 第二章点、直线、平面之间的位置关系复习 |  | |
| 格式 | docx | ||
| 文件大小 | 310.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 12:00:47 | ||
图片预览




文档简介
本章复习提升
易混易错练
易错点1 平面几何定理与立体几何定理相混淆
1.(★★☆)如图所示,在多面体A1B1D1-ABCD中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.证明:EF∥B1C.
2.(★★☆)如图所示,四棱柱ABCD-A1B1C1D1中,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
证明:Q为BB1的中点.
易错点2 忽略判定定理或性质定理的必备条件
3.(★★☆)已知平面α∥平面β,AB、CD是夹在α、β间的两条线段,A、C在α内,B、D在β内,点E、F分别在AB、CD上,且AE∶EB=CF∶FD=m∶n.求证:EF∥平面α.
易错点3 对有关平行、垂直的概念和定理理解不透彻
4.(东北育才学校高一期中,★★☆)已知互不重合的直线a,b,互不重合的平面α,β,给出下列四个命题,正确命题的个数是( )
①若a∥α,a∥β,α∩β=b,则a∥b;
②若α⊥β,a⊥α,b⊥β,则a⊥b;
③若α⊥β,α⊥γ,β∩γ=a,则a⊥α;
④若α∥β,a∥α,则a∥β.
A.1 B.2 C.3 D.4
易错点4 依赖图形直观而致错
5.(吉林高二期末,★★☆)下图是正方体的平面展开图,在这个正方体中,
①BM∥平面DE;
②CN∥平面AF;
③平面BDM∥平面AFN.
以上结论中,正确结论的个数是( )
A.1 B.2 C.3 D.0
6.(★★☆)如图所示,ABCD-A1B1C1D1是正方体,在图中,E,F分别是D1C1,B1B的中点,画出图①②中有阴影的平面与平面ABCD的交线,并给出证明.
思想方法练
一、函数与方程思想在立体几何中的应用
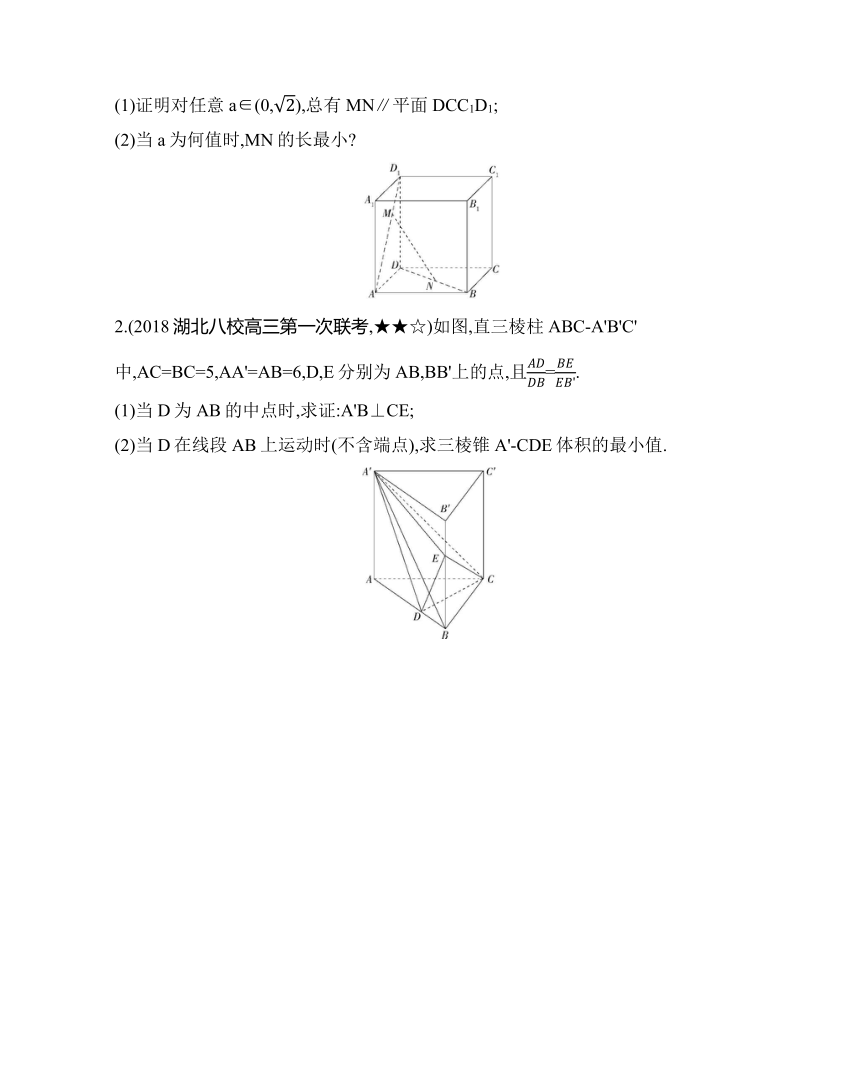
1.(★★☆)如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M在AD1上移动,点N在BD上移动,D1M=DN=a(0(1)证明对任意a∈(0,),总有MN∥平面DCC1D1;
(2)当a为何值时,MN的长最小
2.(2018湖北八校高三第一次联考,★★☆)如图,直三棱柱ABC-A'B'C'中,AC=BC=5,AA'=AB=6,D,E分别为AB,BB'上的点,且=.
(1)当D为AB的中点时,求证:A'B⊥CE;
(2)当D在线段AB上运动时(不含端点),求三棱锥A'-CDE体积的最小值.
二、转化与化归思想在平行关系中的应用
3.(2018辽宁沈阳教学质量监测,★★☆)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若AD=2,PD=3,∠BAD=60°,求三棱锥P-ADM的体积.
4.(2018河北衡水中学模拟,★★☆)如图,在长方体ABCD-A1B1C1D1中,AB=1,AD=2,E,F分别为AD,AA1的中点,Q是BC上的一个动点,且BQ=λQC(λ>0).
(1)当λ=1时,求证:平面BEF∥平面A1DQ;
(2)是否存在λ,使得BD⊥FQ 若存在,求出λ的值;若不存在,请说明理由.
三、转化与化归思想在空间垂直关系中的应用
5.(2018山西太原高三模拟,★★☆)如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
(1)求证:AD⊥平面PNB;
(2)若平面PAD⊥平面ABCD,求三棱锥P-NBM的体积.
6.(2018陕西西安八校高三联考,★★☆)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点为M,已知PA=AB=4,AD=CD,∠CDA=120°,N是CD的中点.
(1)求证:平面PMN⊥平面PAB;
(2)求点M到平面PBC的距离.
答案全解全析
易混易错练
1.证明 由正方形的性质可知A1B1∥AB∥DC,且A1B1=AB=DC,所以四边形A1B1CD为平行四边形,从而B1C∥A1D.又A1D 平面A1DE,B1C 平面A1DE,于是B1C∥平面A1DE.又B1C 平面B1CD1,平面A1DE∩平面B1CD1=EF,所以EF∥B1C.
2.证明 因为BQ∥AA1,BC∥AD,BC∩BQ=B,AD∩AA1=A,
所以平面QBC∥平面A1AD.
从而平面α与这两个平面的交线互相平行,即QC∥A1D.
故△QBC与△A1AD的对应边互相平行,
于是△QBC∽△A1AD.
所以===,
即Q为BB1的中点.
3.证明 (1)当AB、CD共面时(如图①),连接AC、BD.
因为α∥β,所以AC∥BD.
因为AE∶EB=CF∶FD,
所以EF∥AC∥BD且EF在α外.
因为AC α,所以EF∥平面α.
(2)当AB、CD异面时(如图②),过点A作AH∥CD交β于点H.
在AH上取点G,使AG∶GH=m∶n,
连接GF、GE、EF、BH,由(1)可得FG∥HD.
因为AG∶GH=AE∶EB,所以EG∥BH,
所以平面EFG∥平面β∥平面α.
又因为EF 平面EFG,所以EF∥平面α.
4.C 在①中,由于α∩β=b,a∥α,a∥β,
过直线a与平面α,β都相交的平面记为γ,记α∩γ=d,β∩γ=c,
则a∥d且a∥c,所以d∥c,
又d∥b,所以a∥b,故①是正确的;
在②中,若α⊥β,a⊥α,b⊥β,则由面面垂直和线面垂直的性质得a⊥b,所以②是正确的;
在③中,若α⊥β,α⊥γ,β∩γ=a,则由线面垂直的判定定理得a⊥α,所以是③正确的;
在④中,若α∥β,a∥α,则a∥β或a β,所以④是不正确的,故选C.
5.C 把正方体的平面展开图还原成正方体ABCD-EFMN,如图所示.
连接AN,根据正方体的性质可得BM∥AN,根据线面平行的判定定理,
可得BM∥平面DE,所以①正确;
同理可得CN∥平面AF,故②正确;
因为BD∥FN,BM∥AN,BD∩BM=B,FN∩AN=N,
所以平面BDM∥平面AFN,故③正确,所以三个命题都正确,故选C.
6.解析 如图①所示,过点E作EN平行于BB1交CD于点N,连接NB并延长交EF的延长线于M,连接AM,则直线AM即为有阴影的平面与平面ABCD的交线.
如图②所示,延长DC,过点C1作C1M∥A1B交DC的延长线于点M,连接BM,则直线BM即为有阴影的平面与平面ABCD的交线.
证明:在图①中,因为直线EN∥BF,所以B,N,E,F四点共面,因此EF与NB相交,交点为M.因为M∈EF,且M∈NB,而EF 平面AEF,NB 平面ABCD,所以M是平面ABCD与平面AEF的公共点.又因为点A是平面ABCD与平面AEF的公共点,故直线AM为两平面的交线.
在图②中,C1M在平面CDD1C1内,因此与DC的延长线相交,交点为M,则点M为平面A1C1B与平面ABCD的公共点,又点B也是这两个平面的公共点,因此直线BM是两平面的交线.
思想方法练
1.解析 (1)证明:如图,作MP∥AD,交DD1于P,作NQ∥BC,交DC于Q,连接PQ.
由题意得MP∥NQ,且MP=NQ,则四边形MNQP为平行四边形.
∴MN∥PQ.
又PQ 平面DCC1D1,MN 平面DCC1D1,
∴MN∥平面DCC1D1.
(2)由(1)知四边形MNQP为平行四边形,∴MN=PQ.
∵DD1=AD=DC=BC=1,∴AD1=BD=.
∵D1M=DN=a,∴=,=,
即D1P=DQ=,
∴MN=PQ=
=
=(0故当a=时,MN的长有最小值,最小值为.
2.解析 (1)证明:因为D为AB的中点,=,所以E为B'B的中点,
因为三棱柱ABC-A'B'C'为直三棱柱,AA'=AB=6,
所以四边形ABB'A'为正方形,所以DE⊥A'B,
因为AC=BC,D为AB的中点,
所以CD⊥AB,
因为平面ABB'A'⊥平面ABC,
且平面ABB'A'∩平面ABC=AB,
所以CD⊥平面ABB'A',又A'B 平面ABB'A',所以CD⊥A'B,
又CD∩DE=D,所以A'B⊥平面CDE,
又CE 平面CDE,所以A'B⊥CE.
(2)设AD=x(0由已知可得,点C到平面A'DE的距离即△ABC的边AB上的高h,
且h==4,
所以VA'-CDE=VC-A'DE=(S四边形ABB'A'-S△AA'D-S△DBE-S△A'B'E)·h
=36-3x-(6-x)x-3(6-x)·h
=(x2-6x+36)
=(x-3)2+18(0所以当x=3,即D为AB的中点时,VA'-CDE取得最小值,最小值为18.
3.解析 (1)证法一:如图,过点M作MN∥CD交PD于点N,连接AN.
因为PM=2MC,所以MN=CD.
又AB=CD,且AB∥CD,
所以AB MN,所以四边形ABMN为平行四边形,所以BM∥AN.
又BM 平面PAD,AN 平面PAD,所以BM∥平面PAD.
证法二:如图,过点M作MN⊥CD于点N,N为垂足,连接BN.
因为PM=2MC,所以DN=2NC,
又AB∥CD,AB=CD,所以AB DN,
所以四边形ABND为平行四边形,
所以BN∥AD.
因为PD⊥平面ABCD,DC 平面ABCD,
所以PD⊥DC.
又MN⊥DC,MN 平面PDC,
所以PD∥MN.
因为BN 平面MBN,MN 平面MBN,BN∩MN=N,AD 平面PAD,PD 平面PAD,AD∩PD=D,
所以平面MBN∥平面PAD.
因为BM 平面MBN,所以BM∥平面PAD.
(2)如图,过B作AD的垂线,垂足为E.
因为PD⊥平面ABCD,BE 平面ABCD,
所以PD⊥BE.
又AD 平面PAD,PD 平面PAD,AD∩PD=D,所以BE⊥平面PAD.
由(1)知,BM∥平面PAD,
所以点M到平面PAD的距离等于点B到平面PAD的距离,即BE的长.
连接BD,在△ABD中,AB=AD=2,∠BAD=60°,所以BE=.
故VP-ADM=VM-PAD=·S△PAD·BE=××2×3×=.
4.解析 (1)证明:当λ=1时,Q为BC的中点,
因为E是AD的中点,
所以ED=BQ,又ED∥BQ,
所以四边形BEDQ是平行四边形,
所以BE∥QD.
又BE 平面A1DQ,DQ 平面A1DQ,
所以BE∥平面A1DQ.
又F是A1A的中点,所以EF∥A1D.
因为EF 平面A1DQ,A1D 平面A1DQ,
所以EF∥平面A1DQ,又BE∩EF=E,
所以平面BEF∥平面A1DQ.
(2)存在.如图,连接AQ,BD,FQ,
因为A1A⊥平面ABCD,BD 平面ABCD,
所以A1A⊥BD.
因为BD⊥FQ,A1A、FQ 平面A1AQ,
所以BD⊥平面A1AQ.
因为AQ 平面A1AQ,所以AQ⊥BD.
在矩形ABCD中,由AQ⊥BD,
得△AQB∽△DBA,
所以AB2=AD·BQ.
又AB=1,AD=2,所以BQ=,
所以QC=,所以=,即λ=.
5.解析 (1)证明:∵PA=PD,N为AD的中点,∴PN⊥AD,
∵底面ABCD为菱形,∠BAD=60°,
∴BN⊥AD,
∵PN∩BN=N,∴AD⊥平面PNB.
(2)连接AC.∵PA=PD=AD=2,
∴PN=NB=,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PN⊥AD,PN 平面PAD,
∴PN⊥平面ABCD,
∴PN⊥NB,∴S△PNB=××=.
∵AD⊥平面PNB,AD∥BC,
∴BC⊥平面PNB.
∵PM=2MC,∴VP-NBM=VM-PNB=VC-PNB=×××2=.
6.解析 (1)证明:由于AD=CD,AB=BC,
所以BD垂直平分AC,
所以M为AC的中点,因为N是CD的中点,所以MN∥AD.
因为PA⊥平面ABCD,所以PA⊥AD,因为∠CDA=120°,所以∠DAC=30°,
因为∠BAC=60°,所以∠BAD=90°,
即BA⊥AD.
因为PA∩AB=A,所以AD⊥平面PAB,
所以MN⊥平面PAB.又MN 平面PMN,
所以平面PMN⊥平面PAB.
(2)设点M到平面PBC的距离为h,
在Rt△PAB中,PA=AB=4,所以PB=4,
在Rt△PAC中,PA=AC=4,所以PC=4,
在△PBC中,PB=4,PC=4,BC=4,
所以S△PBC=4.
由VM-PBC=VP-BMC,即×4×h=×2×4,解得h=,
所以点M到平面PBC的距离为.
易混易错练
易错点1 平面几何定理与立体几何定理相混淆
1.(★★☆)如图所示,在多面体A1B1D1-ABCD中,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.证明:EF∥B1C.
2.(★★☆)如图所示,四棱柱ABCD-A1B1C1D1中,四边形ABCD为梯形,AD∥BC,且AD=2BC.过A1,C,D三点的平面记为α,BB1与α的交点为Q.
证明:Q为BB1的中点.
易错点2 忽略判定定理或性质定理的必备条件
3.(★★☆)已知平面α∥平面β,AB、CD是夹在α、β间的两条线段,A、C在α内,B、D在β内,点E、F分别在AB、CD上,且AE∶EB=CF∶FD=m∶n.求证:EF∥平面α.
易错点3 对有关平行、垂直的概念和定理理解不透彻
4.(东北育才学校高一期中,★★☆)已知互不重合的直线a,b,互不重合的平面α,β,给出下列四个命题,正确命题的个数是( )
①若a∥α,a∥β,α∩β=b,则a∥b;
②若α⊥β,a⊥α,b⊥β,则a⊥b;
③若α⊥β,α⊥γ,β∩γ=a,则a⊥α;
④若α∥β,a∥α,则a∥β.
A.1 B.2 C.3 D.4
易错点4 依赖图形直观而致错
5.(吉林高二期末,★★☆)下图是正方体的平面展开图,在这个正方体中,
①BM∥平面DE;
②CN∥平面AF;
③平面BDM∥平面AFN.
以上结论中,正确结论的个数是( )
A.1 B.2 C.3 D.0
6.(★★☆)如图所示,ABCD-A1B1C1D1是正方体,在图中,E,F分别是D1C1,B1B的中点,画出图①②中有阴影的平面与平面ABCD的交线,并给出证明.
思想方法练
一、函数与方程思想在立体几何中的应用
1.(★★☆)如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,点M在AD1上移动,点N在BD上移动,D1M=DN=a(0
(2)当a为何值时,MN的长最小
2.(2018湖北八校高三第一次联考,★★☆)如图,直三棱柱ABC-A'B'C'中,AC=BC=5,AA'=AB=6,D,E分别为AB,BB'上的点,且=.
(1)当D为AB的中点时,求证:A'B⊥CE;
(2)当D在线段AB上运动时(不含端点),求三棱锥A'-CDE体积的最小值.
二、转化与化归思想在平行关系中的应用
3.(2018辽宁沈阳教学质量监测,★★☆)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,AB=2,CD=3,M为PC上一点,且PM=2MC.
(1)求证:BM∥平面PAD;
(2)若AD=2,PD=3,∠BAD=60°,求三棱锥P-ADM的体积.
4.(2018河北衡水中学模拟,★★☆)如图,在长方体ABCD-A1B1C1D1中,AB=1,AD=2,E,F分别为AD,AA1的中点,Q是BC上的一个动点,且BQ=λQC(λ>0).
(1)当λ=1时,求证:平面BEF∥平面A1DQ;
(2)是否存在λ,使得BD⊥FQ 若存在,求出λ的值;若不存在,请说明理由.
三、转化与化归思想在空间垂直关系中的应用
5.(2018山西太原高三模拟,★★☆)如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,PA=PD=AD=2,点M在线段PC上,且PM=2MC,N为AD的中点.
(1)求证:AD⊥平面PNB;
(2)若平面PAD⊥平面ABCD,求三棱锥P-NBM的体积.
6.(2018陕西西安八校高三联考,★★☆)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点为M,已知PA=AB=4,AD=CD,∠CDA=120°,N是CD的中点.
(1)求证:平面PMN⊥平面PAB;
(2)求点M到平面PBC的距离.
答案全解全析
易混易错练
1.证明 由正方形的性质可知A1B1∥AB∥DC,且A1B1=AB=DC,所以四边形A1B1CD为平行四边形,从而B1C∥A1D.又A1D 平面A1DE,B1C 平面A1DE,于是B1C∥平面A1DE.又B1C 平面B1CD1,平面A1DE∩平面B1CD1=EF,所以EF∥B1C.
2.证明 因为BQ∥AA1,BC∥AD,BC∩BQ=B,AD∩AA1=A,
所以平面QBC∥平面A1AD.
从而平面α与这两个平面的交线互相平行,即QC∥A1D.
故△QBC与△A1AD的对应边互相平行,
于是△QBC∽△A1AD.
所以===,
即Q为BB1的中点.
3.证明 (1)当AB、CD共面时(如图①),连接AC、BD.
因为α∥β,所以AC∥BD.
因为AE∶EB=CF∶FD,
所以EF∥AC∥BD且EF在α外.
因为AC α,所以EF∥平面α.
(2)当AB、CD异面时(如图②),过点A作AH∥CD交β于点H.
在AH上取点G,使AG∶GH=m∶n,
连接GF、GE、EF、BH,由(1)可得FG∥HD.
因为AG∶GH=AE∶EB,所以EG∥BH,
所以平面EFG∥平面β∥平面α.
又因为EF 平面EFG,所以EF∥平面α.
4.C 在①中,由于α∩β=b,a∥α,a∥β,
过直线a与平面α,β都相交的平面记为γ,记α∩γ=d,β∩γ=c,
则a∥d且a∥c,所以d∥c,
又d∥b,所以a∥b,故①是正确的;
在②中,若α⊥β,a⊥α,b⊥β,则由面面垂直和线面垂直的性质得a⊥b,所以②是正确的;
在③中,若α⊥β,α⊥γ,β∩γ=a,则由线面垂直的判定定理得a⊥α,所以是③正确的;
在④中,若α∥β,a∥α,则a∥β或a β,所以④是不正确的,故选C.
5.C 把正方体的平面展开图还原成正方体ABCD-EFMN,如图所示.
连接AN,根据正方体的性质可得BM∥AN,根据线面平行的判定定理,
可得BM∥平面DE,所以①正确;
同理可得CN∥平面AF,故②正确;
因为BD∥FN,BM∥AN,BD∩BM=B,FN∩AN=N,
所以平面BDM∥平面AFN,故③正确,所以三个命题都正确,故选C.
6.解析 如图①所示,过点E作EN平行于BB1交CD于点N,连接NB并延长交EF的延长线于M,连接AM,则直线AM即为有阴影的平面与平面ABCD的交线.
如图②所示,延长DC,过点C1作C1M∥A1B交DC的延长线于点M,连接BM,则直线BM即为有阴影的平面与平面ABCD的交线.
证明:在图①中,因为直线EN∥BF,所以B,N,E,F四点共面,因此EF与NB相交,交点为M.因为M∈EF,且M∈NB,而EF 平面AEF,NB 平面ABCD,所以M是平面ABCD与平面AEF的公共点.又因为点A是平面ABCD与平面AEF的公共点,故直线AM为两平面的交线.
在图②中,C1M在平面CDD1C1内,因此与DC的延长线相交,交点为M,则点M为平面A1C1B与平面ABCD的公共点,又点B也是这两个平面的公共点,因此直线BM是两平面的交线.
思想方法练
1.解析 (1)证明:如图,作MP∥AD,交DD1于P,作NQ∥BC,交DC于Q,连接PQ.
由题意得MP∥NQ,且MP=NQ,则四边形MNQP为平行四边形.
∴MN∥PQ.
又PQ 平面DCC1D1,MN 平面DCC1D1,
∴MN∥平面DCC1D1.
(2)由(1)知四边形MNQP为平行四边形,∴MN=PQ.
∵DD1=AD=DC=BC=1,∴AD1=BD=.
∵D1M=DN=a,∴=,=,
即D1P=DQ=,
∴MN=PQ=
=
=(0
2.解析 (1)证明:因为D为AB的中点,=,所以E为B'B的中点,
因为三棱柱ABC-A'B'C'为直三棱柱,AA'=AB=6,
所以四边形ABB'A'为正方形,所以DE⊥A'B,
因为AC=BC,D为AB的中点,
所以CD⊥AB,
因为平面ABB'A'⊥平面ABC,
且平面ABB'A'∩平面ABC=AB,
所以CD⊥平面ABB'A',又A'B 平面ABB'A',所以CD⊥A'B,
又CD∩DE=D,所以A'B⊥平面CDE,
又CE 平面CDE,所以A'B⊥CE.
(2)设AD=x(0
且h==4,
所以VA'-CDE=VC-A'DE=(S四边形ABB'A'-S△AA'D-S△DBE-S△A'B'E)·h
=36-3x-(6-x)x-3(6-x)·h
=(x2-6x+36)
=(x-3)2+18(0
3.解析 (1)证法一:如图,过点M作MN∥CD交PD于点N,连接AN.
因为PM=2MC,所以MN=CD.
又AB=CD,且AB∥CD,
所以AB MN,所以四边形ABMN为平行四边形,所以BM∥AN.
又BM 平面PAD,AN 平面PAD,所以BM∥平面PAD.
证法二:如图,过点M作MN⊥CD于点N,N为垂足,连接BN.
因为PM=2MC,所以DN=2NC,
又AB∥CD,AB=CD,所以AB DN,
所以四边形ABND为平行四边形,
所以BN∥AD.
因为PD⊥平面ABCD,DC 平面ABCD,
所以PD⊥DC.
又MN⊥DC,MN 平面PDC,
所以PD∥MN.
因为BN 平面MBN,MN 平面MBN,BN∩MN=N,AD 平面PAD,PD 平面PAD,AD∩PD=D,
所以平面MBN∥平面PAD.
因为BM 平面MBN,所以BM∥平面PAD.
(2)如图,过B作AD的垂线,垂足为E.
因为PD⊥平面ABCD,BE 平面ABCD,
所以PD⊥BE.
又AD 平面PAD,PD 平面PAD,AD∩PD=D,所以BE⊥平面PAD.
由(1)知,BM∥平面PAD,
所以点M到平面PAD的距离等于点B到平面PAD的距离,即BE的长.
连接BD,在△ABD中,AB=AD=2,∠BAD=60°,所以BE=.
故VP-ADM=VM-PAD=·S△PAD·BE=××2×3×=.
4.解析 (1)证明:当λ=1时,Q为BC的中点,
因为E是AD的中点,
所以ED=BQ,又ED∥BQ,
所以四边形BEDQ是平行四边形,
所以BE∥QD.
又BE 平面A1DQ,DQ 平面A1DQ,
所以BE∥平面A1DQ.
又F是A1A的中点,所以EF∥A1D.
因为EF 平面A1DQ,A1D 平面A1DQ,
所以EF∥平面A1DQ,又BE∩EF=E,
所以平面BEF∥平面A1DQ.
(2)存在.如图,连接AQ,BD,FQ,
因为A1A⊥平面ABCD,BD 平面ABCD,
所以A1A⊥BD.
因为BD⊥FQ,A1A、FQ 平面A1AQ,
所以BD⊥平面A1AQ.
因为AQ 平面A1AQ,所以AQ⊥BD.
在矩形ABCD中,由AQ⊥BD,
得△AQB∽△DBA,
所以AB2=AD·BQ.
又AB=1,AD=2,所以BQ=,
所以QC=,所以=,即λ=.
5.解析 (1)证明:∵PA=PD,N为AD的中点,∴PN⊥AD,
∵底面ABCD为菱形,∠BAD=60°,
∴BN⊥AD,
∵PN∩BN=N,∴AD⊥平面PNB.
(2)连接AC.∵PA=PD=AD=2,
∴PN=NB=,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PN⊥AD,PN 平面PAD,
∴PN⊥平面ABCD,
∴PN⊥NB,∴S△PNB=××=.
∵AD⊥平面PNB,AD∥BC,
∴BC⊥平面PNB.
∵PM=2MC,∴VP-NBM=VM-PNB=VC-PNB=×××2=.
6.解析 (1)证明:由于AD=CD,AB=BC,
所以BD垂直平分AC,
所以M为AC的中点,因为N是CD的中点,所以MN∥AD.
因为PA⊥平面ABCD,所以PA⊥AD,因为∠CDA=120°,所以∠DAC=30°,
因为∠BAC=60°,所以∠BAD=90°,
即BA⊥AD.
因为PA∩AB=A,所以AD⊥平面PAB,
所以MN⊥平面PAB.又MN 平面PMN,
所以平面PMN⊥平面PAB.
(2)设点M到平面PBC的距离为h,
在Rt△PAB中,PA=AB=4,所以PB=4,
在Rt△PAC中,PA=AC=4,所以PC=4,
在△PBC中,PB=4,PC=4,BC=4,
所以S△PBC=4.
由VM-PBC=VP-BMC,即×4×h=×2×4,解得h=,
所以点M到平面PBC的距离为.
