青岛版五 关注环境-分数加减法(二) 智慧广场 简单的组合问题 课件(共23张PPT)
文档属性
| 名称 | 青岛版五 关注环境-分数加减法(二) 智慧广场 简单的组合问题 课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-06 12:31:52 | ||
图片预览






文档简介
(共23张PPT)
简单的组合问题
青岛版数学五年级(下)
智慧广场
利用已有经验,认识和了解简单的“组合”,掌握解决问题的策略和方法,体会解决问题策略的多样性。
培养初步的观察、分析及推理能力,能有序地、全面地思考问题。
尝试用数学的方法来解决生活中的实际问题,并初步学会表达解决问题的大致过程和结果。
学习目标
【重点】
掌握解决“组合”问题的策略与方法,训练思维的有序性。
【难点】
培养观察、分析、推理能力,渗透数学建模思想。
从小丽、小军、小杰、小阳4名同学中,选出2人代表学校参加“少儿戏曲大赛”,有多少种不同的组合方法?
课堂导入
答:一共有6种组合方法。
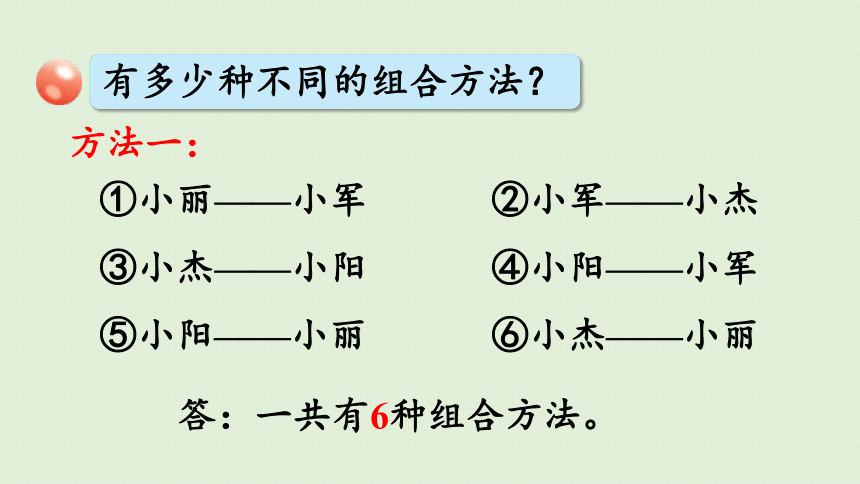
有多少种不同的组合方法?
方法一:
①小丽——小军
②小军——小杰
③小杰——小阳
④小阳——小军
⑤小阳——小丽
⑥小杰——小丽
答:一共有6种组合方法。
有多少种不同的组合方法?
方法二:
小丽
小军
小杰
小阳
小军
小杰
小阳
小杰
小阳
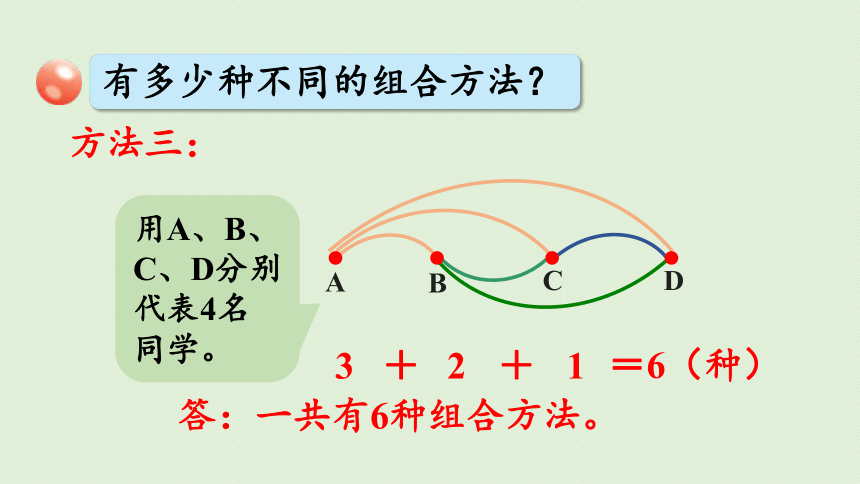
3+2+1=6(种)
3
2
1
=6(种)
A
B
C
D
有多少种不同的组合方法?
方法三:
用A、B、C、D分别代表4名同学。
+
+
答:一共有6种组合方法。
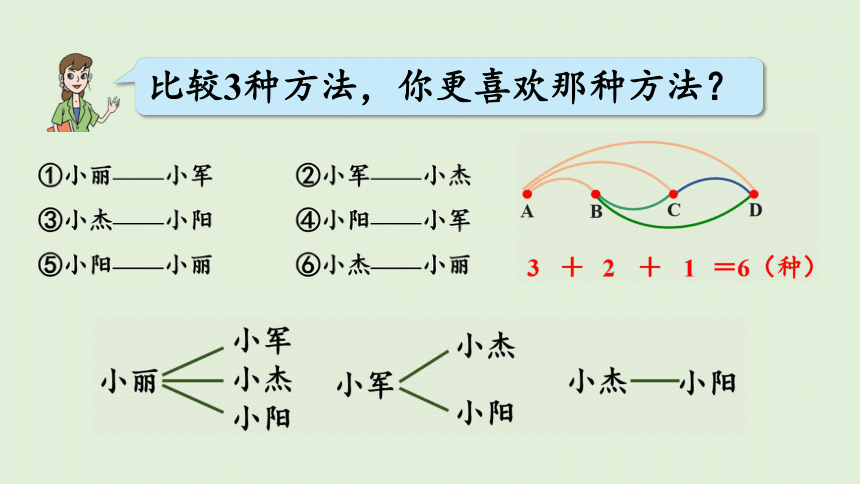
比较3种方法,你更喜欢那种方法?
我更喜欢方法二和方法三,因为按照顺序去思考才能做到不重不漏。
第三种做法还采用了符号表示的方法,简洁、明了。
如果从5名同学中选出2人代表学校参加“少儿戏曲大赛”,有多少种不同的组队方法?
我可以用A、B、C、D、E分别代表5名同学。
方法一:
B
C
D
E
C
D
E
D
E
+ 3
+ 2
+ 1
= 10(种)
A
B
C
D
E
4
答:有10种不同的组队方法。
如果从5名同学中选出2人代表学校参加“少儿戏曲大赛”,有多少种不同的组队方法?
我可以用连线的方法数一数。
方法二:
A
B
C
D
E
+ 3
+ 2
+ 1
= 10(种)
4
答:有10种不同的组队方法。
如果用点来表示学生人数,用两点之间的线段表示一种组队方法,你能完成下表吗?
学生人数 示意图 各点之间的线段条数 组队方案
2
1
1
3
3
4
3+2+1
6
5
4+3+2+1
10
2+1
我发现:如果学生人数有n个,那么组队方案就有1+2+3+……+(n-1)种。
从中你发现了什么规律?
课堂练习
1.爸爸要给小芳买2个玩具,她有多少种选择?
(教材第70页“自主练习”第1题)
答:她有6种选择。
3+2+1=6(种)
(教材第70页“自主练习”第1题)
2.从明明、红红、丽丽、平平4人中挑选2人代表班级参加社区调查,有多少种不同的选法?
答:有10种不同的选法。
4+3+2+1=10(种)
用A、B、C、D、E分别代表这5名同学。
(教材第70页“自主练习”第2题 )
A
B
C
D
E
(教材第70页“自主练习”第3题)
3.某校从5名候选人中选2名参加区“少代会”,有多少种不同的选法?
4+3+2+1=10(种)
用A、B、C、D、E分别代表5名候选人。
答:有10种不同的选法。
A
B
C
D
E
(教材第70页“自主练习”第4题 )
4.甲、乙、丙、丁4个同学进行乒乓球比赛,每两人比赛一场,一共要比赛多少场?
答:一共要比赛6场。
3+2+1=6(场)
用A、B、C、D分别代表这4名同学。
A
B
C
D
掌握了解决组合问题的策略和方法,即通过有序思考可以做到不重不漏。
这节课你有什么收获?
课堂小结
知道了组合问题和排列问题的不同和联系。
完成相关练习。
02
01
课后练习题。
课后作业
简单的组合问题
青岛版数学五年级(下)
智慧广场
利用已有经验,认识和了解简单的“组合”,掌握解决问题的策略和方法,体会解决问题策略的多样性。
培养初步的观察、分析及推理能力,能有序地、全面地思考问题。
尝试用数学的方法来解决生活中的实际问题,并初步学会表达解决问题的大致过程和结果。
学习目标
【重点】
掌握解决“组合”问题的策略与方法,训练思维的有序性。
【难点】
培养观察、分析、推理能力,渗透数学建模思想。
从小丽、小军、小杰、小阳4名同学中,选出2人代表学校参加“少儿戏曲大赛”,有多少种不同的组合方法?
课堂导入
答:一共有6种组合方法。
有多少种不同的组合方法?
方法一:
①小丽——小军
②小军——小杰
③小杰——小阳
④小阳——小军
⑤小阳——小丽
⑥小杰——小丽
答:一共有6种组合方法。
有多少种不同的组合方法?
方法二:
小丽
小军
小杰
小阳
小军
小杰
小阳
小杰
小阳
3+2+1=6(种)
3
2
1
=6(种)
A
B
C
D
有多少种不同的组合方法?
方法三:
用A、B、C、D分别代表4名同学。
+
+
答:一共有6种组合方法。
比较3种方法,你更喜欢那种方法?
我更喜欢方法二和方法三,因为按照顺序去思考才能做到不重不漏。
第三种做法还采用了符号表示的方法,简洁、明了。
如果从5名同学中选出2人代表学校参加“少儿戏曲大赛”,有多少种不同的组队方法?
我可以用A、B、C、D、E分别代表5名同学。
方法一:
B
C
D
E
C
D
E
D
E
+ 3
+ 2
+ 1
= 10(种)
A
B
C
D
E
4
答:有10种不同的组队方法。
如果从5名同学中选出2人代表学校参加“少儿戏曲大赛”,有多少种不同的组队方法?
我可以用连线的方法数一数。
方法二:
A
B
C
D
E
+ 3
+ 2
+ 1
= 10(种)
4
答:有10种不同的组队方法。
如果用点来表示学生人数,用两点之间的线段表示一种组队方法,你能完成下表吗?
学生人数 示意图 各点之间的线段条数 组队方案
2
1
1
3
3
4
3+2+1
6
5
4+3+2+1
10
2+1
我发现:如果学生人数有n个,那么组队方案就有1+2+3+……+(n-1)种。
从中你发现了什么规律?
课堂练习
1.爸爸要给小芳买2个玩具,她有多少种选择?
(教材第70页“自主练习”第1题)
答:她有6种选择。
3+2+1=6(种)
(教材第70页“自主练习”第1题)
2.从明明、红红、丽丽、平平4人中挑选2人代表班级参加社区调查,有多少种不同的选法?
答:有10种不同的选法。
4+3+2+1=10(种)
用A、B、C、D、E分别代表这5名同学。
(教材第70页“自主练习”第2题 )
A
B
C
D
E
(教材第70页“自主练习”第3题)
3.某校从5名候选人中选2名参加区“少代会”,有多少种不同的选法?
4+3+2+1=10(种)
用A、B、C、D、E分别代表5名候选人。
答:有10种不同的选法。
A
B
C
D
E
(教材第70页“自主练习”第4题 )
4.甲、乙、丙、丁4个同学进行乒乓球比赛,每两人比赛一场,一共要比赛多少场?
答:一共要比赛6场。
3+2+1=6(场)
用A、B、C、D分别代表这4名同学。
A
B
C
D
掌握了解决组合问题的策略和方法,即通过有序思考可以做到不重不漏。
这节课你有什么收获?
课堂小结
知道了组合问题和排列问题的不同和联系。
完成相关练习。
02
01
课后练习题。
课后作业
